2024-2025学年广东省惠州市惠城区河南岸中学九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省惠州市惠城区河南岸中学九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 149.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 15:46:42 | ||
图片预览



文档简介
2024-2025学年广东省惠州市惠城区河南岸中学九年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的绝对值是( )
A. B. C. D.
2.据统计,年我国新能源汽车产量超过万辆,其中万用科学记数法表示为( )
A. B. C. D.
3.将直线向下平移个单位长度,平移后直线的解析式为( )
A. B. C. D.
4.若一个正边形的每个内角为,则这个正边形的边数是( )
A. B. C. D.
5.下列计算正确的是( )
A. B. C. D.
6.如图,数字代表所在正方形的面积,则所代表的正方形的面积为( )
A.
B.
C.
D.
7.甲,乙两人进行射击测试,每人次射击成绩平均数均为环,方差分别为,,若甲的成绩更稳定,则,的大小关系为.
A. B. C. D. 无法确定
8.菱形具有而一般平行四边形不具有的性质是( )
A. 对边平行 B. 对边相等
C. 对角线互相平分 D. 对角线平分一组对角
9.对于函数下列说法错误的是( )
A. 随的增大而减小 B. 它的图象与轴的交点是
C. 当时, D. 它的图象不经过第三象限
10.如图,在正方形中,点从点出发,沿着正方形的边顺时针方向运动一周,则的面积与点运动的路程之间形成的函数关系图象大致是( )
A. B.
C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.计算: ______.
12.若式子有意义,则的取值范围为______.
13.因式分解:______.
14.若等腰三角形的两条边长分别为和,则它的周长为______.
15.如图所示,在 中,,,平分,则______.
16.如图,在中,,,,将折叠,使点恰好落在边上,与点重合,为折痕,则______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
解方程:.
18.本小题分
当下电子产品更新换代速度加快,废旧智能手机数量不断增加科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源据研究,从每吨废旧智能手机中能提炼出的白银比黄金多克已知从吨废旧智能手机中提炼出的黄金,与从吨废旧智能手机中提炼出的白银克数相等求从每吨废旧智能手机中能提炼出黄金与白银各多少克.
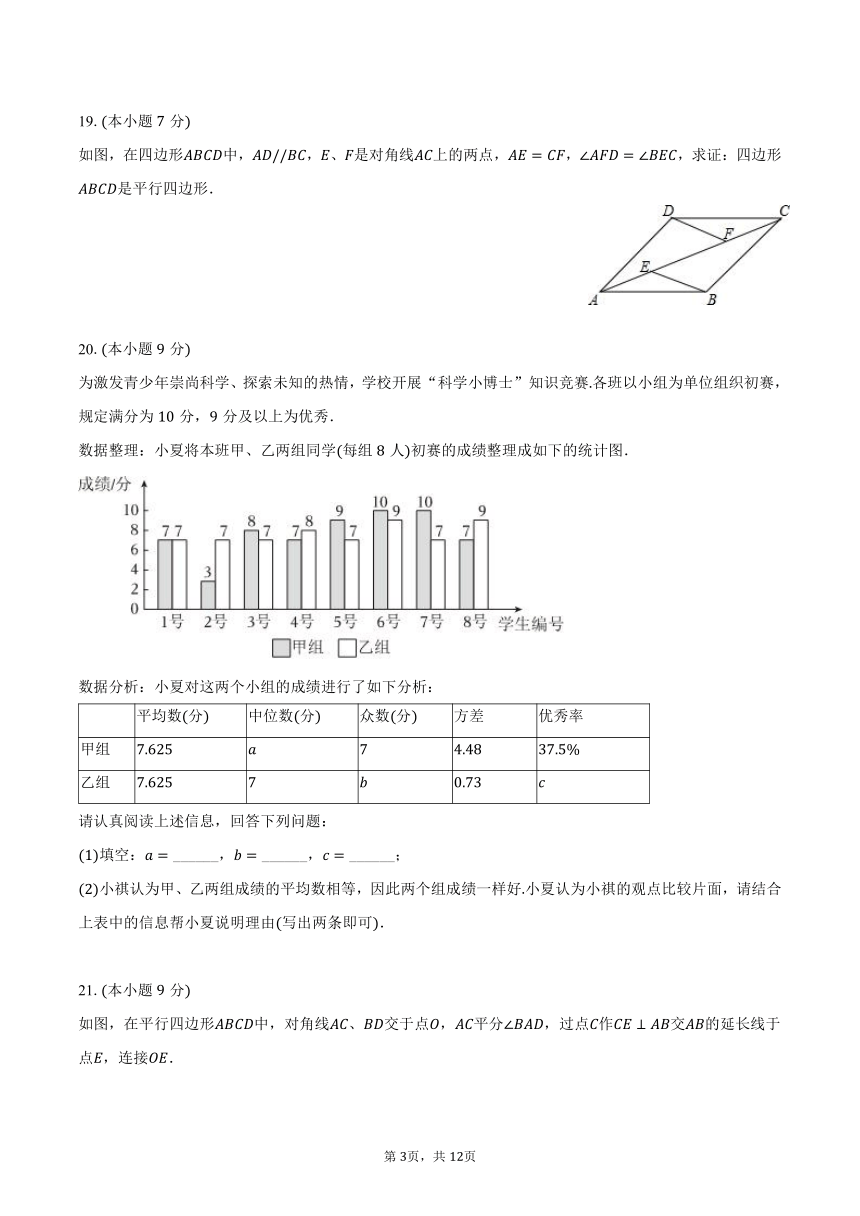
19.本小题分
如图,在四边形中,,、是对角线上的两点,,,求证:四边形是平行四边形.
20.本小题分
为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛各班以小组为单位组织初赛,规定满分为分,分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学每组人初赛的成绩整理成如下的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数分 中位数分 众数分 方差 优秀率
甲组
乙组
请认真阅读上述信息,回答下列问题:
填空: ______, ______, ______;
小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由写出两条即可.
21.本小题分
如图,在平行四边形中,对角线、交于点,平分,过点作交的延长线于点,连接.
求证:四边形是菱形;
若,,求的长度.
22.本小题分
“琅琅书声浸校园,悠悠书韵满人生”,为提升学生的文学素养,培养学生的阅读兴趣,某校启动校园“读书季”,并计划购进,两种图书作为年级竞诵活动的奖品经调查,购进种图书的总费用元与购进种图书本数之间的函数关系如图所示:
当时,求与之间的函数关系式;
现学校准备购进,两种图书共本,已知种图书每本元若购进种图书不少于本,且不超过种图书本数的倍,购进两种图书的总费用为元,请求出符合条件的与之间的函数表达式,并说明怎样购买,两种图书才能使总费用最少?总费用少为多少元?
23.本小题分
如图,在平面直角坐标系中,点,点为正方形的两个顶点,点和在第一象限.
求点的坐标;
求直线的函数表达式;
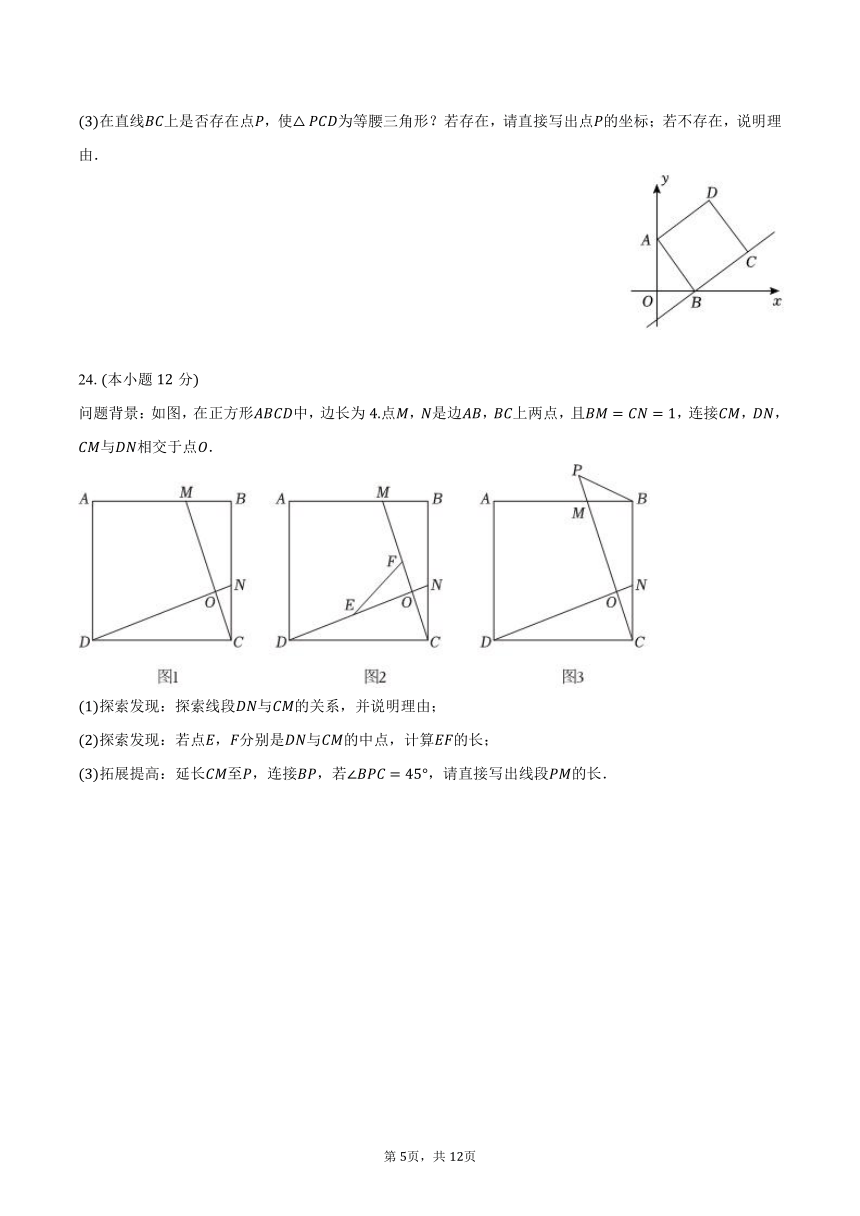
在直线上是否存在点,使为等腰三角形?若存在,请直接写出点的坐标;若不存在,说明理由.
24.本小题分
问题背景:如图,在正方形中,边长为点,是边,上两点,且,连接,,与相交于点.
探索发现:探索线段与的关系,并说明理由;
探索发现:若点,分别是与的中点,计算的长;
拓展提高:延长至,连接,若,请直接写出线段的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:原方程两边都乘,去分母得:,
整理得:,
解得:,
检验:当时,,
故原方程的解为.
18.解:设从每吨废旧智能手机中能提炼出黄金克,白银克,
根据题意得:,
解得:,
即从每吨废旧智能手机中能提炼出黄金克,白银克.
答:从每吨废旧智能手机中能提炼出黄金克,白银克.
19.证明:,
,
,
,
即,
在和中,,
≌,
,
四边形是平行四边形.
20.;;.
小祺的观点比较片面.
理由不唯一,例如:甲组成绩的优秀率为,高于乙组成绩的优秀率,
从优秀率的角度看,甲组成绩比乙组好;
甲组成绩的中位数为,高于乙组成绩的中位数,
从中位数的角度看,甲组成绩比乙组好;
因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
21.证明:四边形是平行四边形,
,
,
为的平分线,
,
,
,
平行四边形是菱形;
解:平行四边形是菱形,
,,,
,
,
,
在中,,
,
22.解:当时,每本种图书价格为元本,
,
与之间的函数关系式为;
购进,两种图书共本,
购进种图书本,
购进种图书不少于本,且不超过种图书本数的倍,
,
解得,
根据题意得:,
,
随的增大而减小,
当时,取最小值,
此时,
购进种图书本,种图书本,总费用最少,最少为元.
23.解:过作轴于点,如图,
四边形是正方形,
,,
.
又,
.
,
.
在和中,
,
≌,
,,
,
;
过点作轴于点,如图,
同理可证得≌,
,,
,
.
设直线的函数表达式为为常数.
代入,,得:
,
解得:,
;
四边形是正方形,
.
在直线上存在点,使为等腰三角形,
只存在.
分类讨论:当点位于点下方时,
,,
此时点与点重合,
;
当点位于点上方时,如图,
,
点为中点.
,,
;
综上可知点的坐标为或.
24.解:,且,
理由:四边形是正方形,
,,
,
≌,
,,
,
,
,
,
线段和的关系为:,且;
连接并延长交于,连接,
四边形是正方形,
,,,
,
,,
≌,
,,
又,
,
正方形的边长为,,
,
在中,由勾股定理得:,
,
,
;
如图,过点作于点,
,
,
,
,
,
,
,
,
.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的绝对值是( )
A. B. C. D.
2.据统计,年我国新能源汽车产量超过万辆,其中万用科学记数法表示为( )
A. B. C. D.
3.将直线向下平移个单位长度,平移后直线的解析式为( )
A. B. C. D.
4.若一个正边形的每个内角为,则这个正边形的边数是( )
A. B. C. D.
5.下列计算正确的是( )
A. B. C. D.
6.如图,数字代表所在正方形的面积,则所代表的正方形的面积为( )
A.
B.
C.
D.
7.甲,乙两人进行射击测试,每人次射击成绩平均数均为环,方差分别为,,若甲的成绩更稳定,则,的大小关系为.
A. B. C. D. 无法确定
8.菱形具有而一般平行四边形不具有的性质是( )
A. 对边平行 B. 对边相等
C. 对角线互相平分 D. 对角线平分一组对角
9.对于函数下列说法错误的是( )
A. 随的增大而减小 B. 它的图象与轴的交点是
C. 当时, D. 它的图象不经过第三象限
10.如图,在正方形中,点从点出发,沿着正方形的边顺时针方向运动一周,则的面积与点运动的路程之间形成的函数关系图象大致是( )
A. B.
C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.计算: ______.
12.若式子有意义,则的取值范围为______.
13.因式分解:______.
14.若等腰三角形的两条边长分别为和,则它的周长为______.
15.如图所示,在 中,,,平分,则______.
16.如图,在中,,,,将折叠,使点恰好落在边上,与点重合,为折痕,则______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
解方程:.
18.本小题分
当下电子产品更新换代速度加快,废旧智能手机数量不断增加科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源据研究,从每吨废旧智能手机中能提炼出的白银比黄金多克已知从吨废旧智能手机中提炼出的黄金,与从吨废旧智能手机中提炼出的白银克数相等求从每吨废旧智能手机中能提炼出黄金与白银各多少克.
19.本小题分
如图,在四边形中,,、是对角线上的两点,,,求证:四边形是平行四边形.
20.本小题分
为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛各班以小组为单位组织初赛,规定满分为分,分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学每组人初赛的成绩整理成如下的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数分 中位数分 众数分 方差 优秀率
甲组
乙组
请认真阅读上述信息,回答下列问题:
填空: ______, ______, ______;
小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由写出两条即可.
21.本小题分
如图,在平行四边形中,对角线、交于点,平分,过点作交的延长线于点,连接.
求证:四边形是菱形;
若,,求的长度.
22.本小题分
“琅琅书声浸校园,悠悠书韵满人生”,为提升学生的文学素养,培养学生的阅读兴趣,某校启动校园“读书季”,并计划购进,两种图书作为年级竞诵活动的奖品经调查,购进种图书的总费用元与购进种图书本数之间的函数关系如图所示:
当时,求与之间的函数关系式;
现学校准备购进,两种图书共本,已知种图书每本元若购进种图书不少于本,且不超过种图书本数的倍,购进两种图书的总费用为元,请求出符合条件的与之间的函数表达式,并说明怎样购买,两种图书才能使总费用最少?总费用少为多少元?
23.本小题分
如图,在平面直角坐标系中,点,点为正方形的两个顶点,点和在第一象限.
求点的坐标;
求直线的函数表达式;
在直线上是否存在点,使为等腰三角形?若存在,请直接写出点的坐标;若不存在,说明理由.
24.本小题分
问题背景:如图,在正方形中,边长为点,是边,上两点,且,连接,,与相交于点.
探索发现:探索线段与的关系,并说明理由;
探索发现:若点,分别是与的中点,计算的长;
拓展提高:延长至,连接,若,请直接写出线段的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:原方程两边都乘,去分母得:,
整理得:,
解得:,
检验:当时,,
故原方程的解为.
18.解:设从每吨废旧智能手机中能提炼出黄金克,白银克,
根据题意得:,
解得:,
即从每吨废旧智能手机中能提炼出黄金克,白银克.
答:从每吨废旧智能手机中能提炼出黄金克,白银克.
19.证明:,
,
,
,
即,
在和中,,
≌,
,
四边形是平行四边形.
20.;;.
小祺的观点比较片面.
理由不唯一,例如:甲组成绩的优秀率为,高于乙组成绩的优秀率,
从优秀率的角度看,甲组成绩比乙组好;
甲组成绩的中位数为,高于乙组成绩的中位数,
从中位数的角度看,甲组成绩比乙组好;
因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
21.证明:四边形是平行四边形,
,
,
为的平分线,
,
,
,
平行四边形是菱形;
解:平行四边形是菱形,
,,,
,
,
,
在中,,
,
22.解:当时,每本种图书价格为元本,
,
与之间的函数关系式为;
购进,两种图书共本,
购进种图书本,
购进种图书不少于本,且不超过种图书本数的倍,
,
解得,
根据题意得:,
,
随的增大而减小,
当时,取最小值,
此时,
购进种图书本,种图书本,总费用最少,最少为元.
23.解:过作轴于点,如图,
四边形是正方形,
,,
.
又,
.
,
.
在和中,
,
≌,
,,
,
;
过点作轴于点,如图,
同理可证得≌,
,,
,
.
设直线的函数表达式为为常数.
代入,,得:
,
解得:,
;
四边形是正方形,
.
在直线上存在点,使为等腰三角形,
只存在.
分类讨论:当点位于点下方时,
,,
此时点与点重合,
;
当点位于点上方时,如图,
,
点为中点.
,,
;
综上可知点的坐标为或.
24.解:,且,
理由:四边形是正方形,
,,
,
≌,
,,
,
,
,
,
线段和的关系为:,且;
连接并延长交于,连接,
四边形是正方形,
,,,
,
,,
≌,
,,
又,
,
正方形的边长为,,
,
在中,由勾股定理得:,
,
,
;
如图,过点作于点,
,
,
,
,
,
,
,
,
.
第1页,共1页
同课章节目录
