3.1物质的聚集状态与晶体的常识 教案 高中化学人教版(2019)选择性必修2
文档属性
| 名称 | 3.1物质的聚集状态与晶体的常识 教案 高中化学人教版(2019)选择性必修2 |

|
|
| 格式 | docx | ||
| 文件大小 | 396.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览

文档简介
核心素养视域下高中化学跨学科教学
-以晶胞中的计算为例
(一)主题与学情分析
本节课选自人教版高中化学《选择性必修二》第三章第一节中“物质的聚集状态与晶体的常识”的相关内容,与数学学科多阶段的相关内容。以晶胞的计算为主题,围绕物质的化学式、配位数、坐标、距离等问题,综合运用化学和数学知识展开教学。高二的学生已经学习过勾股定理、空间几何、三维坐标下求距离,已经具备本节课所需的数学知识。教师对本节课对晶胞中的计算问题只需稍加引导,学生就能得出相应的结论,掌握晶胞中的计算。
(二)教学目标
1.通过对晶胞的认知,学会计算晶胞中的粒子数目,确定物质的化学式,培养学生宏观辨识与微观探析的能力。
2.通过坐标或勾股定理来计算微粒之间的间距,培养学生严谨的科学态度。
3.通过“晶胞中的计算”主题教学活动,加强不同学科的联系,使学生学会用跨学科思维解决问题。
(三)教学重难点
1.重点:晶胞中的微粒数,物质化学式的计算,配位数。
2.难点:原子坐标、微粒间的距离。
(四)教学设计思路
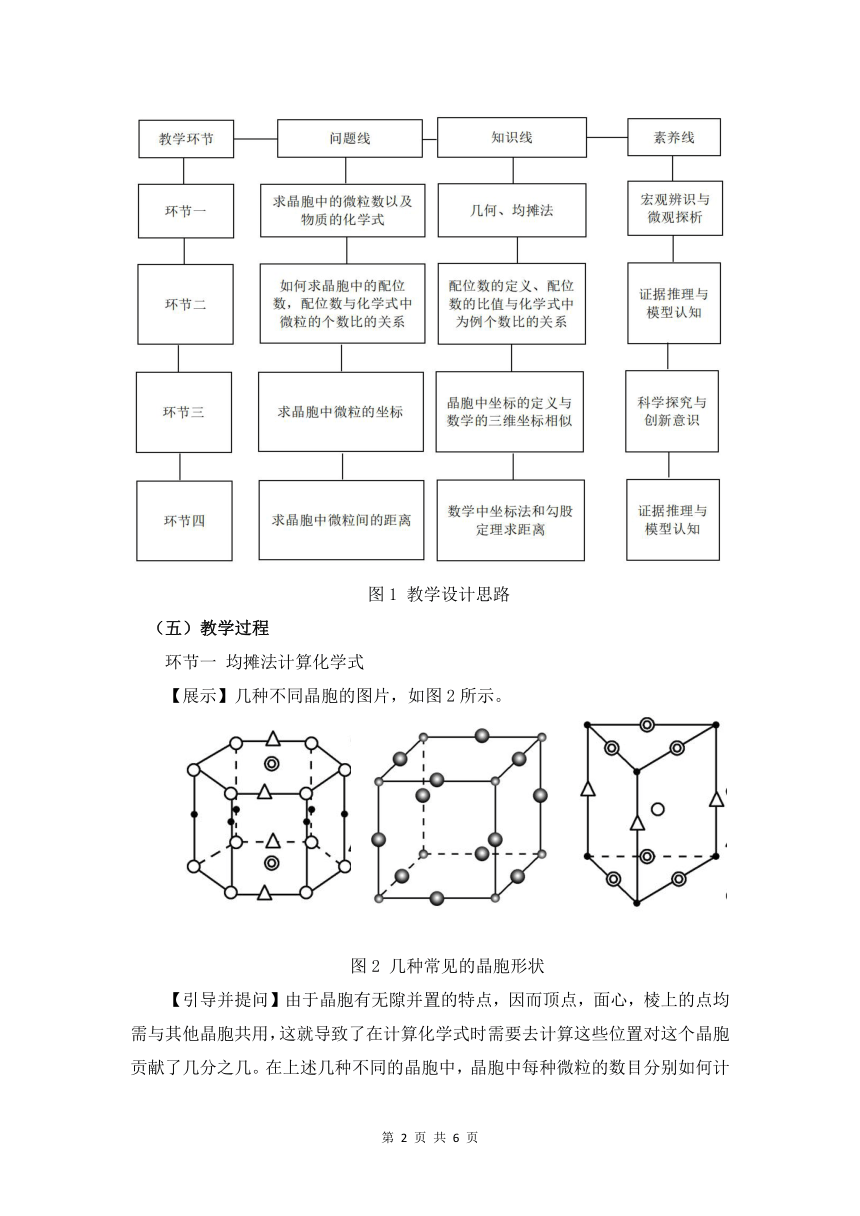
本节课围绕晶胞的计算,设计了四个环节,每个环节中的计算都不一样,与所需要的数学知识储备也有差异,体现了多种核心素养。具体思路设计见图1。
图1 教学设计思路
(五)教学过程
环节一 均摊法计算化学式
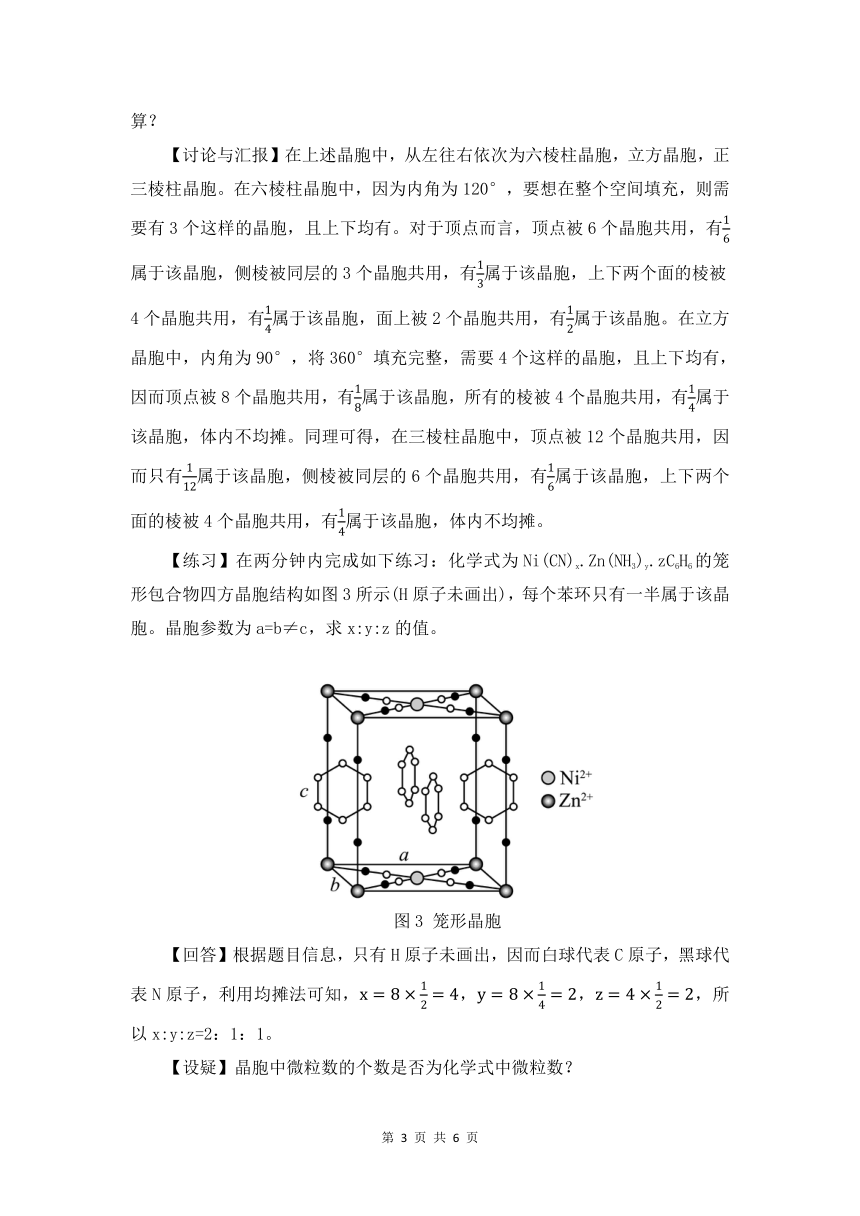
【展示】几种不同晶胞的图片,如图2所示。
图2 几种常见的晶胞形状
【引导并提问】由于晶胞有无隙并置的特点,因而顶点,面心,棱上的点均需与其他晶胞共用,这就导致了在计算化学式时需要去计算这些位置对这个晶胞贡献了几分之几。在上述几种不同的晶胞中,晶胞中每种微粒的数目分别如何计算?
【讨论与汇报】在上述晶胞中,从左往右依次为六棱柱晶胞,立方晶胞,正三棱柱晶胞。在六棱柱晶胞中,因为内角为120°,要想在整个空间填充,则需要有3个这样的晶胞,且上下均有。对于顶点而言,顶点被6个晶胞共用,有属于该晶胞,侧棱被同层的3个晶胞共用,有属于该晶胞,上下两个面的棱被4个晶胞共用,有属于该晶胞,面上被2个晶胞共用,有属于该晶胞。在立方晶胞中,内角为90°,将360°填充完整,需要4个这样的晶胞,且上下均有,因而顶点被8个晶胞共用,有属于该晶胞,所有的棱被4个晶胞共用,有属于该晶胞,体内不均摊。同理可得,在三棱柱晶胞中,顶点被12个晶胞共用,因而只有属于该晶胞,侧棱被同层的6个晶胞共用,有属于该晶胞,上下两个面的棱被4个晶胞共用,有属于该晶胞,体内不均摊。
【练习】在两分钟内完成如下练习:化学式为Ni(CN)x.Zn(NH3)y.zC6H6的笼形包合物四方晶胞结构如图3所示(H原子未画出),每个苯环只有一半属于该晶胞。晶胞参数为a=b≠c,求x:y:z的值。
图3 笼形晶胞
【回答】根据题目信息,只有H原子未画出,因而白球代表C原子,黑球代表N原子,利用均摊法可知,,,,所以x:y:z=2:1:1。
【设疑】晶胞中微粒数的个数是否为化学式中微粒数?
【讨论并回答】不是,化学式是微粒格数的最简比。
【设计意图】让学生从微观层面上去理解为什么物质的化学式写出来是这种比例关系而不是其他的比值关系,培养学生宏观辨识与微观探析的能力。
环节二 配位数
【阐释定义】配位数在晶胞中指的是与某微粒等距且最近的另外微粒数。
【提问】氯化铯晶胞中,如下图4所示,Cs+的配位数是多少?
图4 氯化铯晶胞
【回答】Cs+位于晶胞体心,到8个顶点都相等,因而Cs+的配位数为8。
【提问】由于晶胞无隙并置,因而与Cl-配位的Cs+在其他晶胞也含有,那么Cl-的配位数是多少呢?
【回答】Cl-的配位数等于8。
【思考与讨论】Cl-的配位数和Cs+的配位数与CsCl的化学式有何关系呢?提示学生从比例关系出发寻找不太容易观察的一些微粒的配位数。
【回答】配位数之比等于化学式中的微粒数之比,Cs+的配位数:Cl-的配位数=N(Cl-):N(Cs+)
【练习】C元素和N元素形成的一种超硬晶体的晶胞结构如下图5所示(C原子位于顶点、面心)。求C、N原子的配位数之比。
图5 碳化氮晶胞
【回答】因为晶胞的化学式为C3N4,所以C、N的配位数之比为4:3。
【设计意图】让学生发现配位数之比与化学式组成中微粒的关系,减小了学生在找配位数时难度的同时还提高了准确率。有助于学生进一步理解宏观物质与微观粒子的关系。环节三 原子坐标和距离
环节三 原子坐标
【教师讲解】晶胞是三维结构,因而坐标的形式为(x,y,z),但跟数学有所不同的是(1)化学上晶胞中的原子坐标往往指的是原子分数坐标,即以晶胞参数为单位长度建立的坐标系来表示晶胞中各个原子的位置;(2)晶胞有无隙并置的特点,在坐标中,往往“逢1化0”,即坐标中数值出现1时需将其调整为0,
【提问】根据晶胞中对于坐标的定义,x,y,z的取值范围是多少?
【回答】x,y,z的取值范围均为[0,1)
【思考与讨论】XeF2晶体属于四方晶系,晶胞参数如下图6所示,晶胞棱边夹角均为90 ,A点原子的分数坐标为(,),已知Xe-F键的键长为r pm,则B点原子的分数坐标为 ,晶胞中A、B之间的距离d= pm。
图6 XeF2晶胞
【回答】图1中,灰色球的个数,黑色球的个数,从XeF2的构成上看,Xe和F的个数比为1:2,因而灰色球为Xe,黑色球为F,根据坐标系可知,Xe-F键的键长即为原点与B之间的距离,若以晶胞参数为单位长度,B点在棱的则处,因而B点的坐标为(,)。
【设计意图】晶胞中的坐标与数学上相似,但又有所不同,晶胞中的是原子分数坐标。将数学上找坐标的方式应用到化学中,有助于培养学生严谨的科学态度。
环节四 微粒间的距离
【提问】在高中数学学习了立体几何后,假设在三维空间上有A、B两点,且坐标分别为(x1、y1、z1)、(x2、y2、z2),则AB两点的距离等于多少?
【回答】dAB=
【教师讲解】晶胞中求两点的距离同样也可以用此类方法,但需注意的是晶胞中的坐标是原子分数坐标,因而若用上述公式求距离,需要先换算成数学意义上的坐标。
【学生演示】A点的坐标为(a,),B点的坐标为(,r)dAB==。
【提问】除了用这种方法外,大家在初中还学过勾股定理,是否可以用勾股定理来解决微粒的距离问题呢?
【学生演示】构建直角三角形。如下图7所示,y为面对角线,,则,则dAB==。
图7
【设计意图】让学生数学上求距离的方法迁移到化学中求晶胞微粒间的距离,培养学生证据推理能力。
(六)总结与反思
在晶胞的学习中,晶胞所涉及的计算本身就是一个数学问题,对于学生而言,如何将晶胞中的相关概念、晶胞的特点与数学知识结合到一起来解决问题,是目前很多学生的难点。因而跨学科教学,将数学知识融入到化学中就显得尤为重要。本节课实现了以“晶胞中的计算”为主题的化学与数学跨学科教学,培养了学生应用多学科知识解决问题的能力。
-以晶胞中的计算为例
(一)主题与学情分析
本节课选自人教版高中化学《选择性必修二》第三章第一节中“物质的聚集状态与晶体的常识”的相关内容,与数学学科多阶段的相关内容。以晶胞的计算为主题,围绕物质的化学式、配位数、坐标、距离等问题,综合运用化学和数学知识展开教学。高二的学生已经学习过勾股定理、空间几何、三维坐标下求距离,已经具备本节课所需的数学知识。教师对本节课对晶胞中的计算问题只需稍加引导,学生就能得出相应的结论,掌握晶胞中的计算。
(二)教学目标
1.通过对晶胞的认知,学会计算晶胞中的粒子数目,确定物质的化学式,培养学生宏观辨识与微观探析的能力。
2.通过坐标或勾股定理来计算微粒之间的间距,培养学生严谨的科学态度。
3.通过“晶胞中的计算”主题教学活动,加强不同学科的联系,使学生学会用跨学科思维解决问题。
(三)教学重难点
1.重点:晶胞中的微粒数,物质化学式的计算,配位数。
2.难点:原子坐标、微粒间的距离。
(四)教学设计思路
本节课围绕晶胞的计算,设计了四个环节,每个环节中的计算都不一样,与所需要的数学知识储备也有差异,体现了多种核心素养。具体思路设计见图1。
图1 教学设计思路
(五)教学过程
环节一 均摊法计算化学式
【展示】几种不同晶胞的图片,如图2所示。
图2 几种常见的晶胞形状
【引导并提问】由于晶胞有无隙并置的特点,因而顶点,面心,棱上的点均需与其他晶胞共用,这就导致了在计算化学式时需要去计算这些位置对这个晶胞贡献了几分之几。在上述几种不同的晶胞中,晶胞中每种微粒的数目分别如何计算?
【讨论与汇报】在上述晶胞中,从左往右依次为六棱柱晶胞,立方晶胞,正三棱柱晶胞。在六棱柱晶胞中,因为内角为120°,要想在整个空间填充,则需要有3个这样的晶胞,且上下均有。对于顶点而言,顶点被6个晶胞共用,有属于该晶胞,侧棱被同层的3个晶胞共用,有属于该晶胞,上下两个面的棱被4个晶胞共用,有属于该晶胞,面上被2个晶胞共用,有属于该晶胞。在立方晶胞中,内角为90°,将360°填充完整,需要4个这样的晶胞,且上下均有,因而顶点被8个晶胞共用,有属于该晶胞,所有的棱被4个晶胞共用,有属于该晶胞,体内不均摊。同理可得,在三棱柱晶胞中,顶点被12个晶胞共用,因而只有属于该晶胞,侧棱被同层的6个晶胞共用,有属于该晶胞,上下两个面的棱被4个晶胞共用,有属于该晶胞,体内不均摊。
【练习】在两分钟内完成如下练习:化学式为Ni(CN)x.Zn(NH3)y.zC6H6的笼形包合物四方晶胞结构如图3所示(H原子未画出),每个苯环只有一半属于该晶胞。晶胞参数为a=b≠c,求x:y:z的值。
图3 笼形晶胞
【回答】根据题目信息,只有H原子未画出,因而白球代表C原子,黑球代表N原子,利用均摊法可知,,,,所以x:y:z=2:1:1。
【设疑】晶胞中微粒数的个数是否为化学式中微粒数?
【讨论并回答】不是,化学式是微粒格数的最简比。
【设计意图】让学生从微观层面上去理解为什么物质的化学式写出来是这种比例关系而不是其他的比值关系,培养学生宏观辨识与微观探析的能力。
环节二 配位数
【阐释定义】配位数在晶胞中指的是与某微粒等距且最近的另外微粒数。
【提问】氯化铯晶胞中,如下图4所示,Cs+的配位数是多少?
图4 氯化铯晶胞
【回答】Cs+位于晶胞体心,到8个顶点都相等,因而Cs+的配位数为8。
【提问】由于晶胞无隙并置,因而与Cl-配位的Cs+在其他晶胞也含有,那么Cl-的配位数是多少呢?
【回答】Cl-的配位数等于8。
【思考与讨论】Cl-的配位数和Cs+的配位数与CsCl的化学式有何关系呢?提示学生从比例关系出发寻找不太容易观察的一些微粒的配位数。
【回答】配位数之比等于化学式中的微粒数之比,Cs+的配位数:Cl-的配位数=N(Cl-):N(Cs+)
【练习】C元素和N元素形成的一种超硬晶体的晶胞结构如下图5所示(C原子位于顶点、面心)。求C、N原子的配位数之比。
图5 碳化氮晶胞
【回答】因为晶胞的化学式为C3N4,所以C、N的配位数之比为4:3。
【设计意图】让学生发现配位数之比与化学式组成中微粒的关系,减小了学生在找配位数时难度的同时还提高了准确率。有助于学生进一步理解宏观物质与微观粒子的关系。环节三 原子坐标和距离
环节三 原子坐标
【教师讲解】晶胞是三维结构,因而坐标的形式为(x,y,z),但跟数学有所不同的是(1)化学上晶胞中的原子坐标往往指的是原子分数坐标,即以晶胞参数为单位长度建立的坐标系来表示晶胞中各个原子的位置;(2)晶胞有无隙并置的特点,在坐标中,往往“逢1化0”,即坐标中数值出现1时需将其调整为0,
【提问】根据晶胞中对于坐标的定义,x,y,z的取值范围是多少?
【回答】x,y,z的取值范围均为[0,1)
【思考与讨论】XeF2晶体属于四方晶系,晶胞参数如下图6所示,晶胞棱边夹角均为90 ,A点原子的分数坐标为(,),已知Xe-F键的键长为r pm,则B点原子的分数坐标为 ,晶胞中A、B之间的距离d= pm。
图6 XeF2晶胞
【回答】图1中,灰色球的个数,黑色球的个数,从XeF2的构成上看,Xe和F的个数比为1:2,因而灰色球为Xe,黑色球为F,根据坐标系可知,Xe-F键的键长即为原点与B之间的距离,若以晶胞参数为单位长度,B点在棱的则处,因而B点的坐标为(,)。
【设计意图】晶胞中的坐标与数学上相似,但又有所不同,晶胞中的是原子分数坐标。将数学上找坐标的方式应用到化学中,有助于培养学生严谨的科学态度。
环节四 微粒间的距离
【提问】在高中数学学习了立体几何后,假设在三维空间上有A、B两点,且坐标分别为(x1、y1、z1)、(x2、y2、z2),则AB两点的距离等于多少?
【回答】dAB=
【教师讲解】晶胞中求两点的距离同样也可以用此类方法,但需注意的是晶胞中的坐标是原子分数坐标,因而若用上述公式求距离,需要先换算成数学意义上的坐标。
【学生演示】A点的坐标为(a,),B点的坐标为(,r)dAB==。
【提问】除了用这种方法外,大家在初中还学过勾股定理,是否可以用勾股定理来解决微粒的距离问题呢?
【学生演示】构建直角三角形。如下图7所示,y为面对角线,,则,则dAB==。
图7
【设计意图】让学生数学上求距离的方法迁移到化学中求晶胞微粒间的距离,培养学生证据推理能力。
(六)总结与反思
在晶胞的学习中,晶胞所涉及的计算本身就是一个数学问题,对于学生而言,如何将晶胞中的相关概念、晶胞的特点与数学知识结合到一起来解决问题,是目前很多学生的难点。因而跨学科教学,将数学知识融入到化学中就显得尤为重要。本节课实现了以“晶胞中的计算”为主题的化学与数学跨学科教学,培养了学生应用多学科知识解决问题的能力。
