第十三章 轴对称 单元试卷 (含答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章 轴对称 单元试卷 (含答案) 2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 11:28:41 | ||
图片预览




文档简介
第十三章 轴对称
一、单选题
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.等腰三角形的两边长分别是4和8,则它的周长是( )
A.16 B.20 C.16或20 D.18
3.下列说法正确的是( )
A.有两个角相等的三角形一定是等边三角形
B.如果两个三角形全等,那么它们必是关于某条直线成轴对称
C.等腰三角形的对称轴是顶角的平分线
D.有一个角是的等腰三角形是等边三角形
4.如图,在中,,,分别以点,点为圆心,大于的长为半径作弧,两弧交于点,,过点, 作直线交于点,连接,则的周长为( )
A. B. C. D.
5.如图,在中,,点在上,点在上,且.若,,则的度数为( )
A.30° B.40° C.60° D.80°
6.如图,在中,,,以点为圆心,长为半径作弧,交于点,连接,则的度数为( )
A. B. C. D.
7.如图,和关于直线对称,则下列结论中不正确的是( )
A.
B.直线平分
C.和的周长相等
D.和的面积相等
8.如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠α的度数为( )
A.80° B.100° C.90° D.50°
9.在△ABC中,∠ABC=30°,∠BAC=70°.在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.7条 B.8条 C.9条 D.10条
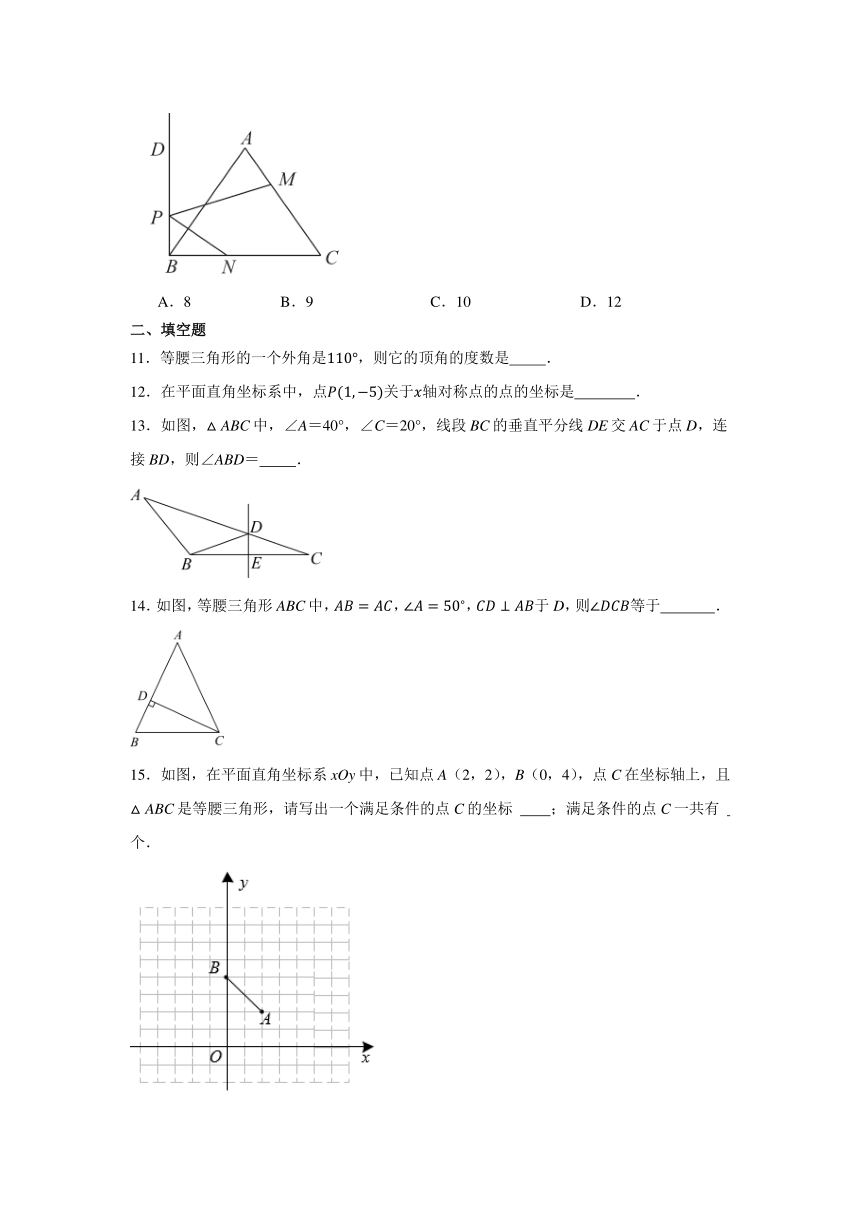
10.如图,点N在等边的边上,,射线,垂足为点B,点P是射线上一动点,点M是线段上一动点,当的值最小时,,则的长为( )
A.8 B.9 C.10 D.12
二、填空题
11.等腰三角形的一个外角是,则它的顶角的度数是 .
12.在平面直角坐标系中,点关于轴对称点的点的坐标是 .
13.如图,△ABC中,∠A=40°,∠C=20°,线段BC的垂直平分线DE交AC于点D,连接BD,则∠ABD= .
14.如图,等腰三角形ABC中,,,于D,则等于 .
15.如图,在平面直角坐标系xOy中,已知点A(2,2),B(0,4),点C在坐标轴上,且△ABC是等腰三角形,请写出一个满足条件的点C的坐标 ;满足条件的点C一共有 个.
16.如图,△ABD,△ACE都是等边三角形,BE和CD交于O点,则∠BOC= 度.
17.如图,在钝角中,已知为钝角,边、的垂直平分线分别交于点、,若,则的度数为 .
三、解答题
18.△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴的对称图形△A′B′C′并写出顶点坐标.
(2)求出△ABC的面积.
19.如图,在△ABC中,AB=AC,点P是底边BC的中点,PD⊥AB,PE⊥AC,BF⊥AC,垂足分别为点D、E、F.
(1)试说明PD与PE的关系.
(2)请证明PD+PE与BF的关系.
20.如图,在中,是边的垂直平分线,,是的中点,,求的度数.
21.如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.
22.数学课上,老师出示了如下框中的题目:
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).
23.如图,是边长为厘米的等边三角形,点,分别从顶点,同时出发,沿线段,运动,且它们的速度都为厘米秒.当点到达点时,、两点停止运动.设点的运动时间为.
(1)当运动时间为秒时,的长为________厘米,的长为________厘米;用含的式子表示
(2)当为何值时,是直角三角形;
(3)如图,连接、,相交于点,则点,在运动的过程中,会变化吗?若变化,则说明理由;若不变,请求出它的度数.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C C C B B A C
11.或
12.(1,5).
13.
14.
15. (0,2)(答案不唯一) 5
16.120
17.120°
18.解:(1)
A′(3,2),B′(4,-3),C′(1,﹣1)
(2)S△ABC=3×5﹣×1×5﹣×2×3﹣×2×3
=15﹣﹣3﹣3=
19.解:(1)∵点P是BC的中点,
∴BP=PC,
∵AB=AC
∴∠B=∠C,且BP=PC,∠BDP=∠PEC=90°
∴△BDP≌△CEP(AAS)
∴PD=PE
(2)PD+PE=BF
理由如下:如图,连接AP,
∵S△ABC=S△ABP+S△APC,
∴AC×BF=AB×PD+×AC×PE
∴BF=PD+PE.
20.解:如图,连接,
是边的垂直平分线,
,
,
,
,
是的中点,
,,
,
是的一个外角,
,
,
,
.
21.
证明:延长AC至E,使CE=BM,连接DE,
∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,
∴∠BCD=30°,
∴∠ABD=∠ACD=90°,
即∠ABD=∠DCE=90°,
∴在Rt△DCE和Rt△DBM中,
∵BD=CD,BM=EC
∴Rt△DCE≌Rt△DBM(HL),
∴∠BDM=∠CDE,
又∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠NDC=∠BDC﹣∠MDN=60°,
∴∠CDE+∠NDC=60°,即∠NDE=60°,
∴∠MDN=∠NDE=60°
∴DM=DE(上面已经全等)
在△DMN和△DEN中
∵DM=DE,∠MDN=∠NDE,DN=DN
∴△DMN≌△DEN(SAS),
∴NM=EN
即NM=CE+CN
∴BM+CN=NM.
22.解:(1)如图1中,结论:AE=BD.
∵△ABC是等边三角形,AE=EB,
∴∠BCE=∠ACE=30°,∠ABC=60°,
∵ED=EC,
∴∠D=∠ECD=30°,
∵∠EBC=∠D+∠BED,
∴∠D=∠BED=30°,
∴BD=BE=AE.
(2)AE=DB.
理由如下:如图2,过点E作EF∥BC,交AC于点F,
在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB﹣AE=AC﹣AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
在△DBE和△EFC中
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD,
故答案为:=.
(3)分为四种情况:
①当点E在AB的延长线上,点D在CB的延长线上时,如图:
∵AB=AC=3,AE=5,
同(2)可得BD=AE,
∴BD=AE=5,
∴CD=3+5=8;
②当点E在BA的延长线上,点D在BC的延长线上时,如图,过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,
∴∠AEM=90°-∠B=30°,
∴BM=BE=×(3+5)=4,
∴CM=BM-BC=4﹣3=1,
∵EC=ED,EM⊥CD,
∴CD=2CM=2;
③当点E在AB的延长线上,点D在BC的延长线上时,如图,
∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
④当点E在BA的延长线上,点D在CB的延长线上时,如图,
∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
综上所述:CD的长是8或2.
23.(1)解:由题意得,,
∵,
∴,
故答案为:,;
(2)解:当时,
∵是等边三角形,
∴,
∴,
∴,
∴,
解得,;
当时,
,
,
,
∴
解得 ;
综上所述,当 或 时,为直角三角形.
(3)解:不变,且,理由如下:
∵是等边三角形,
∴,
在与中,
,
∴,
∴,
∴,
∴不会变化.
一、单选题
1.下列图形是轴对称图形的是( )
A. B. C. D.
2.等腰三角形的两边长分别是4和8,则它的周长是( )
A.16 B.20 C.16或20 D.18
3.下列说法正确的是( )
A.有两个角相等的三角形一定是等边三角形
B.如果两个三角形全等,那么它们必是关于某条直线成轴对称
C.等腰三角形的对称轴是顶角的平分线
D.有一个角是的等腰三角形是等边三角形
4.如图,在中,,,分别以点,点为圆心,大于的长为半径作弧,两弧交于点,,过点, 作直线交于点,连接,则的周长为( )
A. B. C. D.
5.如图,在中,,点在上,点在上,且.若,,则的度数为( )
A.30° B.40° C.60° D.80°
6.如图,在中,,,以点为圆心,长为半径作弧,交于点,连接,则的度数为( )
A. B. C. D.
7.如图,和关于直线对称,则下列结论中不正确的是( )
A.
B.直线平分
C.和的周长相等
D.和的面积相等
8.如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=13:3:2,则∠α的度数为( )
A.80° B.100° C.90° D.50°
9.在△ABC中,∠ABC=30°,∠BAC=70°.在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.7条 B.8条 C.9条 D.10条
10.如图,点N在等边的边上,,射线,垂足为点B,点P是射线上一动点,点M是线段上一动点,当的值最小时,,则的长为( )
A.8 B.9 C.10 D.12
二、填空题
11.等腰三角形的一个外角是,则它的顶角的度数是 .
12.在平面直角坐标系中,点关于轴对称点的点的坐标是 .
13.如图,△ABC中,∠A=40°,∠C=20°,线段BC的垂直平分线DE交AC于点D,连接BD,则∠ABD= .
14.如图,等腰三角形ABC中,,,于D,则等于 .
15.如图,在平面直角坐标系xOy中,已知点A(2,2),B(0,4),点C在坐标轴上,且△ABC是等腰三角形,请写出一个满足条件的点C的坐标 ;满足条件的点C一共有 个.
16.如图,△ABD,△ACE都是等边三角形,BE和CD交于O点,则∠BOC= 度.
17.如图,在钝角中,已知为钝角,边、的垂直平分线分别交于点、,若,则的度数为 .
三、解答题
18.△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)作出△ABC关于y轴的对称图形△A′B′C′并写出顶点坐标.
(2)求出△ABC的面积.
19.如图,在△ABC中,AB=AC,点P是底边BC的中点,PD⊥AB,PE⊥AC,BF⊥AC,垂足分别为点D、E、F.
(1)试说明PD与PE的关系.
(2)请证明PD+PE与BF的关系.
20.如图,在中,是边的垂直平分线,,是的中点,,求的度数.
21.如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.
22.数学课上,老师出示了如下框中的题目:
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE_______DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).
23.如图,是边长为厘米的等边三角形,点,分别从顶点,同时出发,沿线段,运动,且它们的速度都为厘米秒.当点到达点时,、两点停止运动.设点的运动时间为.
(1)当运动时间为秒时,的长为________厘米,的长为________厘米;用含的式子表示
(2)当为何值时,是直角三角形;
(3)如图,连接、,相交于点,则点,在运动的过程中,会变化吗?若变化,则说明理由;若不变,请求出它的度数.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C C C B B A C
11.或
12.(1,5).
13.
14.
15. (0,2)(答案不唯一) 5
16.120
17.120°
18.解:(1)
A′(3,2),B′(4,-3),C′(1,﹣1)
(2)S△ABC=3×5﹣×1×5﹣×2×3﹣×2×3
=15﹣﹣3﹣3=
19.解:(1)∵点P是BC的中点,
∴BP=PC,
∵AB=AC
∴∠B=∠C,且BP=PC,∠BDP=∠PEC=90°
∴△BDP≌△CEP(AAS)
∴PD=PE
(2)PD+PE=BF
理由如下:如图,连接AP,
∵S△ABC=S△ABP+S△APC,
∴AC×BF=AB×PD+×AC×PE
∴BF=PD+PE.
20.解:如图,连接,
是边的垂直平分线,
,
,
,
,
是的中点,
,,
,
是的一个外角,
,
,
,
.
21.
证明:延长AC至E,使CE=BM,连接DE,
∵△BDC是顶角∠BDC=120°的等腰三角形,△ABC是等边三角形,
∴∠BCD=30°,
∴∠ABD=∠ACD=90°,
即∠ABD=∠DCE=90°,
∴在Rt△DCE和Rt△DBM中,
∵BD=CD,BM=EC
∴Rt△DCE≌Rt△DBM(HL),
∴∠BDM=∠CDE,
又∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠NDC=∠BDC﹣∠MDN=60°,
∴∠CDE+∠NDC=60°,即∠NDE=60°,
∴∠MDN=∠NDE=60°
∴DM=DE(上面已经全等)
在△DMN和△DEN中
∵DM=DE,∠MDN=∠NDE,DN=DN
∴△DMN≌△DEN(SAS),
∴NM=EN
即NM=CE+CN
∴BM+CN=NM.
22.解:(1)如图1中,结论:AE=BD.
∵△ABC是等边三角形,AE=EB,
∴∠BCE=∠ACE=30°,∠ABC=60°,
∵ED=EC,
∴∠D=∠ECD=30°,
∵∠EBC=∠D+∠BED,
∴∠D=∠BED=30°,
∴BD=BE=AE.
(2)AE=DB.
理由如下:如图2,过点E作EF∥BC,交AC于点F,
在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB﹣AE=AC﹣AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
在△DBE和△EFC中
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD,
故答案为:=.
(3)分为四种情况:
①当点E在AB的延长线上,点D在CB的延长线上时,如图:
∵AB=AC=3,AE=5,
同(2)可得BD=AE,
∴BD=AE=5,
∴CD=3+5=8;
②当点E在BA的延长线上,点D在BC的延长线上时,如图,过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,
∴∠AEM=90°-∠B=30°,
∴BM=BE=×(3+5)=4,
∴CM=BM-BC=4﹣3=1,
∵EC=ED,EM⊥CD,
∴CD=2CM=2;
③当点E在AB的延长线上,点D在BC的延长线上时,如图,
∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
④当点E在BA的延长线上,点D在CB的延长线上时,如图,
∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
综上所述:CD的长是8或2.
23.(1)解:由题意得,,
∵,
∴,
故答案为:,;
(2)解:当时,
∵是等边三角形,
∴,
∴,
∴,
∴,
解得,;
当时,
,
,
,
∴
解得 ;
综上所述,当 或 时,为直角三角形.
(3)解:不变,且,理由如下:
∵是等边三角形,
∴,
在与中,
,
∴,
∴,
∴,
∴不会变化.
