人教版小学数学五年级上册 梯形的面积 教学设计 docx
文档属性
| 名称 | 人教版小学数学五年级上册 梯形的面积 教学设计 docx |

|
|
| 格式 | docx | ||
| 文件大小 | 800.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览


文档简介
《梯形的面积》教学设计
一、教材分析
教材85页例1、86页例2、课堂活动2题、练习二十一1、6题。《梯形的面积》是在学生认识梯形的特征,掌握了平行四边形,三角形的面积计算,并形成一定空间观念的基础上进行的教学。因此,教材没有安排用数方格的方法求梯形的面积,而是引导学生把梯形转化为已学过的图形来计算它的面积,学生在自主探索的过程中,发现并掌握梯形的面积计算方法,在数学的再创造过程中实现对新知的构建。
二、学情分析
学生已经学行四边形、三角形的面积计算方法,初步理解了平移、旋转的思想,具有了一定的探索图形的面积计算公式的经验,并初步领悟了“转化”的数学思想方法,让学生用同样的推理方法推出梯形面积的公式是可能的。只是学生在推导计算公式时肯定有一定的难度,尤其是用割补法推导公式,因此我先让学生用拼摆两个相同的梯形的方法来推导公式,在此基础上再用割补法来推导公式,这样在掌握知识的同时,学生的思维也能得到充足的发展,使学生自己探索学习,最终获取知识和能力。
三、教学目标
1.通过剪、拼、摆等操作活动,运用转化思想,寻找图形之间的联系,推导梯形面积计算公式,并运用公式解决简单的实际问题。
2.通过梯形面积公式推导过程,培养学生观察、比较、分析、概括能力,发展学生空间观念,培养初步的类推能力和抽象概括能力。
3.在解决简单实际问题的过程中,体会学数学,用数学的乐趣。
四、教学重点、难点
教学重点:探索并掌握梯形面积计算公式。
教学难点:理解梯形面积计算公式的推导过程。
五、教学准备
教师准备:梯形学具、多媒体课件。
学生准备:梯形学具。
六、教学过程
(一)新课导入
师:同学们,我们已学行四边形和三角形的面积的计算方法,谁来说说它们的面积计算公式是怎样推导出来的?
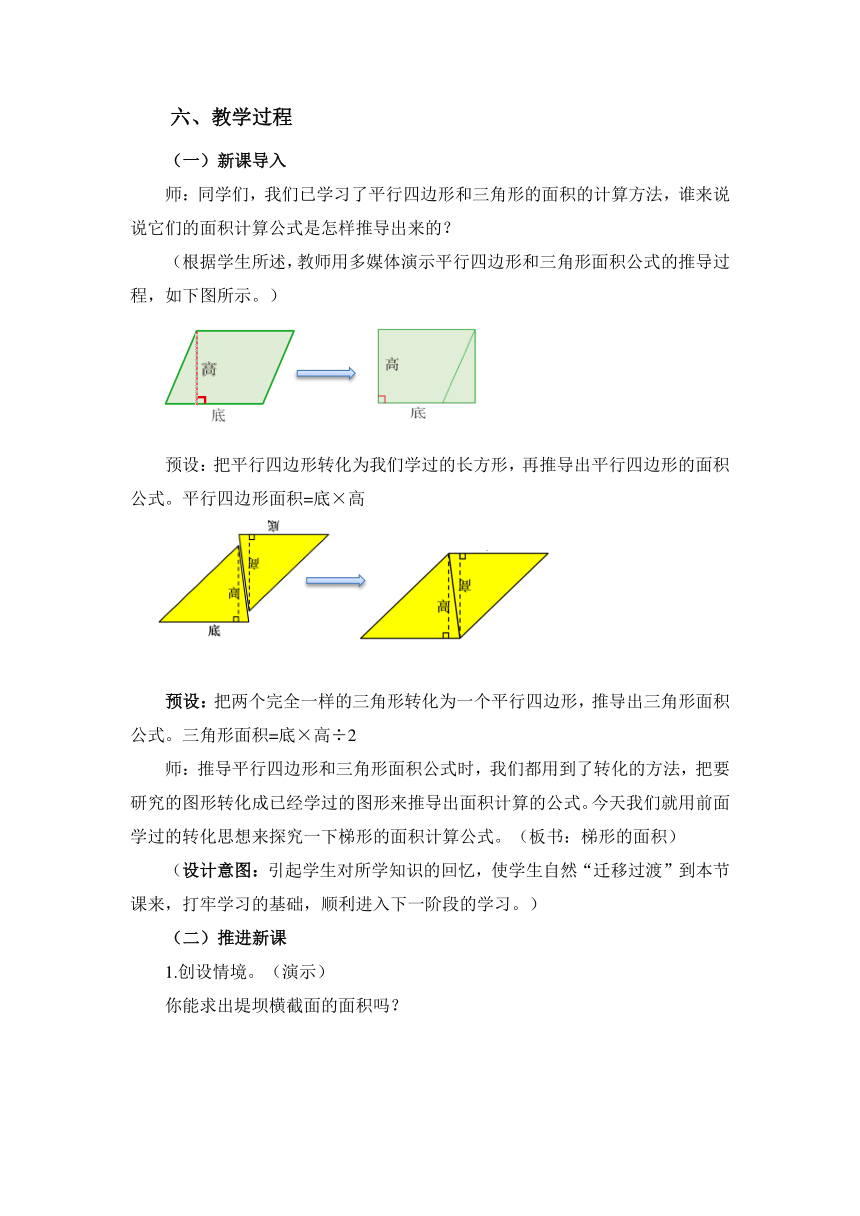
(根据学生所述,教师用多媒体演示平行四边形和三角形面积公式的推导过程,如下图所示。)
预设:把平行四边形转化为我们学过的长方形,再推导出平行四边形的面积公式。平行四边形面积=底×高
预设:把两个完全一样的三角形转化为一个平行四边形,推导出三角形面积公式。三角形面积=底×高÷2
师:推导平行四边形和三角形面积公式时,我们都用到了转化的方法,把要研究的图形转化成已经学过的图形来推导出面积计算的公式。今天我们就用前面学过的转化思想来探究一下梯形的面积计算公式。(板书:梯形的面积)
(设计意图:引起学生对所学知识的回忆,使学生自然“迁移过渡”到本节课来,打牢学习的基础,顺利进入下一阶段的学习。)
(二)推进新课
1.创设情境。(演示)
你能求出堤坝横截面的面积吗?
师:求堤坝横截面的面积是求什么?
(“梯形的面积”,教师演示从实物图抽象出梯形图,同时板书:梯形的面积)
(设计意图:动态演示横截面的示意图,帮助学生理解横截面的含义,明确直角梯形的高也是它的一个腰长。联系数学与生活实际,拉进数学与生活的距离。)
2.提出问题。
在实际生活中,有很多这样的梯形需要计算它们的面积,大家猜一猜梯形的面积可能与什么有关?你有什么好方法推导出梯形面积的计算方法呢?
预设:
(1)梯形的面积可能与它的上底、下底和高有关。
(2)把它转化成一个已经学过的图形,如:平行四边形、长方形、三角形。
(3)找到转化后图形与原来梯形之间的联系,推导出梯形的面积公式。
师:同学们的想法非常好,任何猜想都要经过验证,才能确定是否正确。请大家动手试一试。
(设计意图:明确学习目的,使学生学习有方向,同时,激发了学生的学习动机,引导学生抓住重点深入思考。)
3.探究学习
(1)介绍学具。
师:课前老师老师让大家准备了完全相同的一般梯形、直角梯形、等腰梯形各2个。
(2)自主探索。
①2个完全一样的梯形可以拼成一个怎样的图形。
②梯形还可以转化成哪类图形推导出它的计算公式。
③思考:转化的图形与原梯形有什么关系
4.合作学习。
学生小组讨论,动手操作,教师巡视参与,了解情况。
5.汇报展示。(教师利用多媒体帮助学生演示图形的变化过程。)
(1)展台展示“拼组”的方法。
方法一:选择两个形状相同、大小相等(完全一样)的梯形可以拼成一个平行四边形。
平行四边形的面积=底×高
梯形的面积=(上底+下底)×高÷2
师:这个方法很好!老师还发现有的同学拼成的是长方形,让我们来看看他们又是怎么拼的呢?
方法二:选择两个形状相同、大小相等的直角梯形可以拼成一个长方形。
长方形的面积=长×宽
梯形的面积=(上底+下底)×高÷2
师:同学们不仅动手能力特别强,公式的推导过程也叙述得特别条理、清晰。那么两个怎样的梯形可以拼成正方形呢?
预设:学生通过观察、想象、实际操作,会得出结论:形状相同、大小相等的直角梯形且上底与下底的和正好与梯形的高相等,这样的两个梯形可以拼成一个正方形。
师:刚才展示的方法都是把两个完全相同的梯形经过“拼组”之后转化成一个已学过的图形,平行四边形、长方形或正方形。有的小组只用自己手中的一个梯形就完成了任务,我们快来分享他们的成果吧!
(2)展台展示“割补”的方法。
方法三:把一个梯形分割成两个三角形a和b。
a的面积=上底×高÷2
b的面积=下底×高÷2
所以,梯形的面积=a的面积+b的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
师:在公式的推导过程中应用了乘法分配律,非常好!
方法四:把一个梯形剪成两个梯形再拼成一个平行四边形。
平行四边形的面积=底×高
梯形的面积=(上底+下底)×高÷2
预设:对上述两种推导过程有部分学生有理解的困难,教师要发挥引导者、合作者的作用,及时进行点拨指导,帮助学生逐步理清思路。(演示)
师:在这些方法中,你最喜欢哪一种?说一说喜欢的理由?(教师大屏幕呈现学生喜欢的方法)
6.归纳总结,提高认识
(1)整理公式。
师:我们用“转化”的方法推导出梯形的面积计算公式为:
梯形的面积=(上底+下底)×高÷2。
(2)自学字母公式。
用s表示梯形的面积,用ɑ表示梯形的上底,b表示梯形的下底,h表示梯形的高,s=(ɑ+b)×h÷2。
7.返回解决情境例题。
出示例2:拦河坝的横截面是一个梯形,它的上底是13m,下底比上底长135m,高是26m,求拦河坝横截面的面积。
(设计意图:教师放手让学生利用已有知识经验,动手把梯形转化成已经学过的图形,并让学生通过找图形之间的联系,自主从不同的途径探索出梯形的面积计算方法。学生亲自参与了面积公式的推导过程,真正做到“知其然,必知其所以然”,而且思维能力、空间感受能力、动手操作能力都得到锻炼和提高。)
(三)巩固练习
梯形的的用途很广泛,在很多物体中经常会看到梯形。下面我们来解决一些日常生活中的问题。(多媒体出示)
(1)练习二十一第1题。
(2)练习二十一第6题。
(四)拓展延伸
一共有多少根彩笔?
(设计意图:练习题的设计,把所学知识与实际生活紧密联系起来,既有基础知识和基本技能的训练,又有综合性的题目,使学生体会到数学与生活的联系。培养了学生用数学眼光认识事物,应用数学的意识,从而进一步体会数学的应用价值。)
(五)课堂小结
这节课同学们用自己的智慧,推导出了梯形面积计算公式,而且能够灵活用所学知识解决生活中的的问题。老师希望在今后的学习中,大家能克服困难,给自己制定更高的学习目标,并为之努力奋斗。
七、板书设计
梯形的面积
梯形的面积=(上底+下底)×高÷2
s=(ɑ+b)×h÷2
一、教材分析
教材85页例1、86页例2、课堂活动2题、练习二十一1、6题。《梯形的面积》是在学生认识梯形的特征,掌握了平行四边形,三角形的面积计算,并形成一定空间观念的基础上进行的教学。因此,教材没有安排用数方格的方法求梯形的面积,而是引导学生把梯形转化为已学过的图形来计算它的面积,学生在自主探索的过程中,发现并掌握梯形的面积计算方法,在数学的再创造过程中实现对新知的构建。
二、学情分析
学生已经学行四边形、三角形的面积计算方法,初步理解了平移、旋转的思想,具有了一定的探索图形的面积计算公式的经验,并初步领悟了“转化”的数学思想方法,让学生用同样的推理方法推出梯形面积的公式是可能的。只是学生在推导计算公式时肯定有一定的难度,尤其是用割补法推导公式,因此我先让学生用拼摆两个相同的梯形的方法来推导公式,在此基础上再用割补法来推导公式,这样在掌握知识的同时,学生的思维也能得到充足的发展,使学生自己探索学习,最终获取知识和能力。
三、教学目标
1.通过剪、拼、摆等操作活动,运用转化思想,寻找图形之间的联系,推导梯形面积计算公式,并运用公式解决简单的实际问题。
2.通过梯形面积公式推导过程,培养学生观察、比较、分析、概括能力,发展学生空间观念,培养初步的类推能力和抽象概括能力。
3.在解决简单实际问题的过程中,体会学数学,用数学的乐趣。
四、教学重点、难点
教学重点:探索并掌握梯形面积计算公式。
教学难点:理解梯形面积计算公式的推导过程。
五、教学准备
教师准备:梯形学具、多媒体课件。
学生准备:梯形学具。
六、教学过程
(一)新课导入
师:同学们,我们已学行四边形和三角形的面积的计算方法,谁来说说它们的面积计算公式是怎样推导出来的?
(根据学生所述,教师用多媒体演示平行四边形和三角形面积公式的推导过程,如下图所示。)
预设:把平行四边形转化为我们学过的长方形,再推导出平行四边形的面积公式。平行四边形面积=底×高
预设:把两个完全一样的三角形转化为一个平行四边形,推导出三角形面积公式。三角形面积=底×高÷2
师:推导平行四边形和三角形面积公式时,我们都用到了转化的方法,把要研究的图形转化成已经学过的图形来推导出面积计算的公式。今天我们就用前面学过的转化思想来探究一下梯形的面积计算公式。(板书:梯形的面积)
(设计意图:引起学生对所学知识的回忆,使学生自然“迁移过渡”到本节课来,打牢学习的基础,顺利进入下一阶段的学习。)
(二)推进新课
1.创设情境。(演示)
你能求出堤坝横截面的面积吗?
师:求堤坝横截面的面积是求什么?
(“梯形的面积”,教师演示从实物图抽象出梯形图,同时板书:梯形的面积)
(设计意图:动态演示横截面的示意图,帮助学生理解横截面的含义,明确直角梯形的高也是它的一个腰长。联系数学与生活实际,拉进数学与生活的距离。)
2.提出问题。
在实际生活中,有很多这样的梯形需要计算它们的面积,大家猜一猜梯形的面积可能与什么有关?你有什么好方法推导出梯形面积的计算方法呢?
预设:
(1)梯形的面积可能与它的上底、下底和高有关。
(2)把它转化成一个已经学过的图形,如:平行四边形、长方形、三角形。
(3)找到转化后图形与原来梯形之间的联系,推导出梯形的面积公式。
师:同学们的想法非常好,任何猜想都要经过验证,才能确定是否正确。请大家动手试一试。
(设计意图:明确学习目的,使学生学习有方向,同时,激发了学生的学习动机,引导学生抓住重点深入思考。)
3.探究学习
(1)介绍学具。
师:课前老师老师让大家准备了完全相同的一般梯形、直角梯形、等腰梯形各2个。
(2)自主探索。
①2个完全一样的梯形可以拼成一个怎样的图形。
②梯形还可以转化成哪类图形推导出它的计算公式。
③思考:转化的图形与原梯形有什么关系
4.合作学习。
学生小组讨论,动手操作,教师巡视参与,了解情况。
5.汇报展示。(教师利用多媒体帮助学生演示图形的变化过程。)
(1)展台展示“拼组”的方法。
方法一:选择两个形状相同、大小相等(完全一样)的梯形可以拼成一个平行四边形。
平行四边形的面积=底×高
梯形的面积=(上底+下底)×高÷2
师:这个方法很好!老师还发现有的同学拼成的是长方形,让我们来看看他们又是怎么拼的呢?
方法二:选择两个形状相同、大小相等的直角梯形可以拼成一个长方形。
长方形的面积=长×宽
梯形的面积=(上底+下底)×高÷2
师:同学们不仅动手能力特别强,公式的推导过程也叙述得特别条理、清晰。那么两个怎样的梯形可以拼成正方形呢?
预设:学生通过观察、想象、实际操作,会得出结论:形状相同、大小相等的直角梯形且上底与下底的和正好与梯形的高相等,这样的两个梯形可以拼成一个正方形。
师:刚才展示的方法都是把两个完全相同的梯形经过“拼组”之后转化成一个已学过的图形,平行四边形、长方形或正方形。有的小组只用自己手中的一个梯形就完成了任务,我们快来分享他们的成果吧!
(2)展台展示“割补”的方法。
方法三:把一个梯形分割成两个三角形a和b。
a的面积=上底×高÷2
b的面积=下底×高÷2
所以,梯形的面积=a的面积+b的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
师:在公式的推导过程中应用了乘法分配律,非常好!
方法四:把一个梯形剪成两个梯形再拼成一个平行四边形。
平行四边形的面积=底×高
梯形的面积=(上底+下底)×高÷2
预设:对上述两种推导过程有部分学生有理解的困难,教师要发挥引导者、合作者的作用,及时进行点拨指导,帮助学生逐步理清思路。(演示)
师:在这些方法中,你最喜欢哪一种?说一说喜欢的理由?(教师大屏幕呈现学生喜欢的方法)
6.归纳总结,提高认识
(1)整理公式。
师:我们用“转化”的方法推导出梯形的面积计算公式为:
梯形的面积=(上底+下底)×高÷2。
(2)自学字母公式。
用s表示梯形的面积,用ɑ表示梯形的上底,b表示梯形的下底,h表示梯形的高,s=(ɑ+b)×h÷2。
7.返回解决情境例题。
出示例2:拦河坝的横截面是一个梯形,它的上底是13m,下底比上底长135m,高是26m,求拦河坝横截面的面积。
(设计意图:教师放手让学生利用已有知识经验,动手把梯形转化成已经学过的图形,并让学生通过找图形之间的联系,自主从不同的途径探索出梯形的面积计算方法。学生亲自参与了面积公式的推导过程,真正做到“知其然,必知其所以然”,而且思维能力、空间感受能力、动手操作能力都得到锻炼和提高。)
(三)巩固练习
梯形的的用途很广泛,在很多物体中经常会看到梯形。下面我们来解决一些日常生活中的问题。(多媒体出示)
(1)练习二十一第1题。
(2)练习二十一第6题。
(四)拓展延伸
一共有多少根彩笔?
(设计意图:练习题的设计,把所学知识与实际生活紧密联系起来,既有基础知识和基本技能的训练,又有综合性的题目,使学生体会到数学与生活的联系。培养了学生用数学眼光认识事物,应用数学的意识,从而进一步体会数学的应用价值。)
(五)课堂小结
这节课同学们用自己的智慧,推导出了梯形面积计算公式,而且能够灵活用所学知识解决生活中的的问题。老师希望在今后的学习中,大家能克服困难,给自己制定更高的学习目标,并为之努力奋斗。
七、板书设计
梯形的面积
梯形的面积=(上底+下底)×高÷2
s=(ɑ+b)×h÷2
