2024-2025学年广东省深圳中学九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省深圳中学九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 111.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 16:00:23 | ||
图片预览



文档简介
2024-2025学年广东省深圳中学九年级(上)开学数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.年巴黎奥运会是第三十三届夏季奥林匹克运动会,将于年月日至月日在法国巴黎举行下面年巴黎奥运会项目图标是中心对称图形的是( )
A. B. C. D.
2.若,则下列不等式不一定成立的是( )
A. B. C. D.
3.若代数式在实数范围内有意义,则的取值范围为( )
A. 且 B. C. D. 且
4.把多项式分解因式,结果是,则,的值为( )
A. , B. ,
C. , D. ,
5.如图,在 中,按照如下尺规作图的步骤进行操作:以点为圆心,以适当长为半径画弧,分别与,交于点,;分别以,为圆心,以适当长为半径画弧,两弧交于点,作射线,与边交于点;以为圆心,长为半径画弧,交于边于点若,,则点,之间的距离为( )
A. B.
C. D.
6.下列命题中,假命题是( )
A. 顺次连接任意四边形各边中点形成的四边形都是平行四边形
B. 等腰三角形的高、中线、角平分线重合
C. 对角线互相垂直且平分的四边形是菱形
D. 用反证法证明命题“三角形中必有一个内角小于或等于”时,首先要假设“这个三角形中每一个内角都大于”
7.如图,用长为的篱笆,一面利用墙墙的最大可用长度为,围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在上用其他材料做了宽为的两扇小门,若花圃的面积刚好为,则此时花圃段的长为.
A. 或 B.
C. D.
8.如图,在矩形中,,点为边上一动点,点为的中点,连接,点在上,且,则下列结论:在点从点运动到点的过程中,点运动的路径长为;的最小值为;点到的中点的距离为定值;的最小值为其中正确的是( )
A. B.
C. D.
二、填空题:本题共5小题,每小题3分,共15分。
9.因式分解: ______.
10.若为方程的解,则的值为______.
11.如图,在 中,,,的平分线交于,交的延长线于点,则 ______.
12.若关于的方程解为正数,则的取值范围是______.
13.在中,,,,为的中点,分别交直线,于点,,且,连接,当时,的长为______.
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
解不等式组:;
解方程:.
15.本小题分
先化简,然后从,,,中选取一个合适的数作为的值代入求值.
16.本小题分
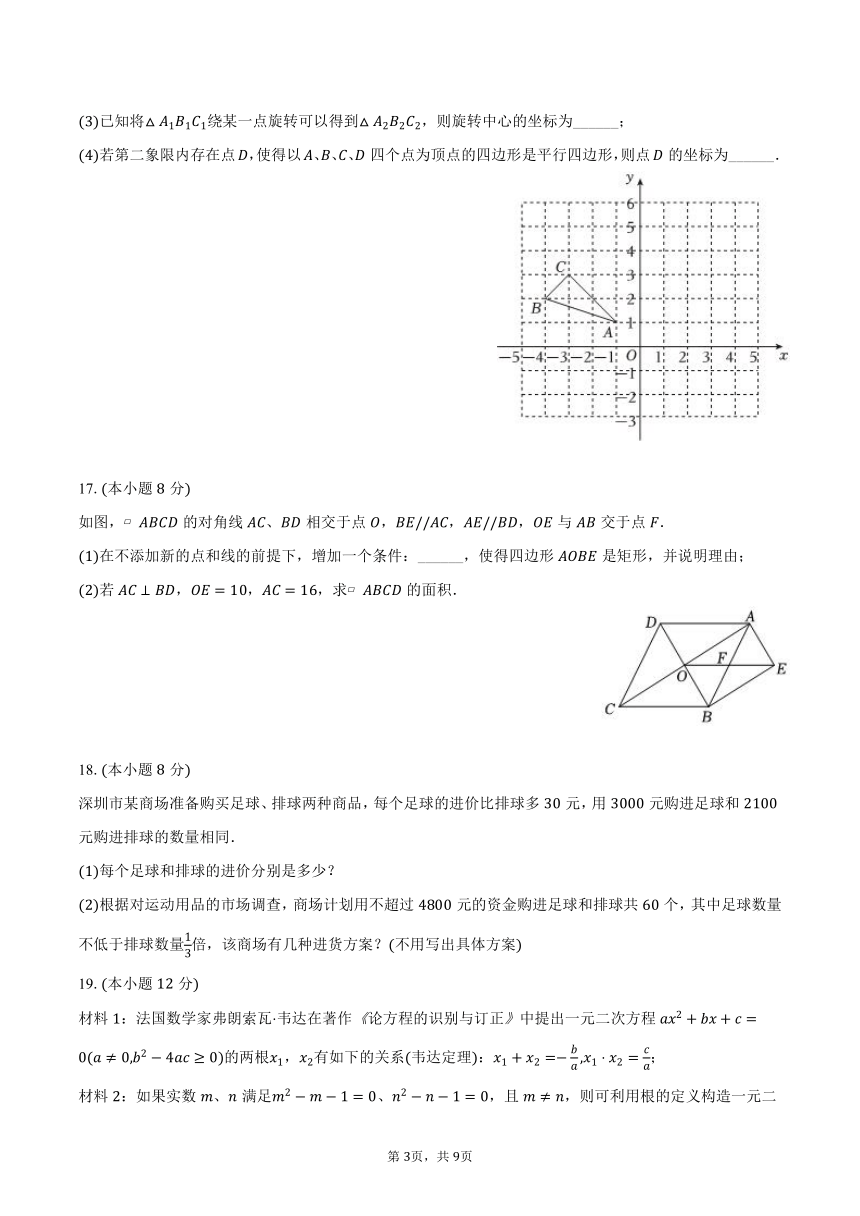
如图,在平面直角坐标系中,的顶点,,.
平移,若点的对应点的坐标为,画出平移后的;
将以点为旋转中心旋转,画出旋转后对应的;
已知将绕某一点旋转可以得到,则旋转中心的坐标为______;
若第二象限内存在点,使得以、、、四个点为顶点的四边形是平行四边形,则点的坐标为______.
17.本小题分
如图, 的对角线、相交于点,,,与交于点.
在不添加新的点和线的前提下,增加一个条件:______,使得四边形是矩形,并说明理由;
若,,,求 的面积.
18.本小题分
深圳市某商场准备购买足球、排球两种商品,每个足球的进价比排球多元,用元购进足球和元购进排球的数量相同.
每个足球和排球的进价分别是多少?
根据对运动用品的市场调查,商场计划用不超过元的资金购进足球和排球共个,其中足球数量不低于排球数量倍,该商场有几种进货方案?不用写出具体方案
19.本小题分
材料:法国数学家弗朗索瓦韦达在著作论方程的识别与订正中提出一元二次方程的两根,有如下的关系韦达定理:;
材料:如果实数、满足、,且,则可利用根的定义构造一元二次方程,然后将、看作是此方程的两个不相等实数根.
请根据上述材料解决下面问题:
已知一元二次方程的两根分别为,,则 ______, ______.
已知实数,满足:,,则 ______.
已知实数、、满足:,,且,求的取值范围.
设实数,分别满足,,且,求的值.
20.本小题分
垂美四边形定义如下:对角线互相垂直的四边形叫做“垂美四边形”.
如图,四边形是“垂美四边形”,猜想、与、之间的数量关系:______,并说明理由.
如图,分别以的直角边和斜边为边向外作正方形和正方形,连接、,若,求的长.
如图,在中,,点是外一点,连接,,已知,若以、、、为顶点的四边形为垂美四边形,请直接写出的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.且
13.
14.解:解不等式得,,
解不等式得,,
所以不等式组的解集为:.
,
,
则或,
所以,.
15.解:原式
,
且且,
在,,,中只能取,
当时,原式.
16.如图,即为所求.
如图,即为所求.
.
如图:的坐标为或或时,以、、、四个点为顶点的四边形是平行四边形,
在第二象限,
.
17.解:添加:答案不唯一.
理由:,,
四边形是平行四边形,
,
,
四边形是矩形;
由可知,四边形是矩形,
,
四边形是平行四边形,
,
,
,
,
四边形的面积.
18.解:设每个足球的进价是元,则每个排球的进价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
,
答:每个足球的进价是元,每个排球的进价是元;
设购进足球个,则购进排球个,
由题意得:,
解得:,
又为正整数,
,,,,,,
该商场有种进货方案.
19.;;
;
实数、、满足:,
,是方程的解,
,,
,
,,
,
,
;
,,
,
,
,
是方程的解,
,
,,
.
20.;
解:如图,
四边形,是正方形,为直角三角形,
,,,
,
≌,
,
,
,
,
,
,
四边形为“垂美四边形”,
,
在中,由勾股定理得,,
,同理可求,,
,
解得;
当时,则,
在中,由勾股定理得,,
,
解得:舍负,
,
过点作延长线的垂线,垂足为点,
由题意得,,
,
,
而,,
≌,
,,
,
在中,由勾股定理得,
;
当时,
同上可求此时,,
过点作于点,
同上可证≌,
,,
,
在中,由勾股定理得,,
综上所述,或.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.年巴黎奥运会是第三十三届夏季奥林匹克运动会,将于年月日至月日在法国巴黎举行下面年巴黎奥运会项目图标是中心对称图形的是( )
A. B. C. D.
2.若,则下列不等式不一定成立的是( )
A. B. C. D.
3.若代数式在实数范围内有意义,则的取值范围为( )
A. 且 B. C. D. 且
4.把多项式分解因式,结果是,则,的值为( )
A. , B. ,
C. , D. ,
5.如图,在 中,按照如下尺规作图的步骤进行操作:以点为圆心,以适当长为半径画弧,分别与,交于点,;分别以,为圆心,以适当长为半径画弧,两弧交于点,作射线,与边交于点;以为圆心,长为半径画弧,交于边于点若,,则点,之间的距离为( )
A. B.
C. D.
6.下列命题中,假命题是( )
A. 顺次连接任意四边形各边中点形成的四边形都是平行四边形
B. 等腰三角形的高、中线、角平分线重合
C. 对角线互相垂直且平分的四边形是菱形
D. 用反证法证明命题“三角形中必有一个内角小于或等于”时,首先要假设“这个三角形中每一个内角都大于”
7.如图,用长为的篱笆,一面利用墙墙的最大可用长度为,围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在上用其他材料做了宽为的两扇小门,若花圃的面积刚好为,则此时花圃段的长为.
A. 或 B.
C. D.
8.如图,在矩形中,,点为边上一动点,点为的中点,连接,点在上,且,则下列结论:在点从点运动到点的过程中,点运动的路径长为;的最小值为;点到的中点的距离为定值;的最小值为其中正确的是( )
A. B.
C. D.
二、填空题:本题共5小题,每小题3分,共15分。
9.因式分解: ______.
10.若为方程的解,则的值为______.
11.如图,在 中,,,的平分线交于,交的延长线于点,则 ______.
12.若关于的方程解为正数,则的取值范围是______.
13.在中,,,,为的中点,分别交直线,于点,,且,连接,当时,的长为______.
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
解不等式组:;
解方程:.
15.本小题分
先化简,然后从,,,中选取一个合适的数作为的值代入求值.
16.本小题分
如图,在平面直角坐标系中,的顶点,,.
平移,若点的对应点的坐标为,画出平移后的;
将以点为旋转中心旋转,画出旋转后对应的;
已知将绕某一点旋转可以得到,则旋转中心的坐标为______;
若第二象限内存在点,使得以、、、四个点为顶点的四边形是平行四边形,则点的坐标为______.
17.本小题分
如图, 的对角线、相交于点,,,与交于点.
在不添加新的点和线的前提下,增加一个条件:______,使得四边形是矩形,并说明理由;
若,,,求 的面积.
18.本小题分
深圳市某商场准备购买足球、排球两种商品,每个足球的进价比排球多元,用元购进足球和元购进排球的数量相同.
每个足球和排球的进价分别是多少?
根据对运动用品的市场调查,商场计划用不超过元的资金购进足球和排球共个,其中足球数量不低于排球数量倍,该商场有几种进货方案?不用写出具体方案
19.本小题分
材料:法国数学家弗朗索瓦韦达在著作论方程的识别与订正中提出一元二次方程的两根,有如下的关系韦达定理:;
材料:如果实数、满足、,且,则可利用根的定义构造一元二次方程,然后将、看作是此方程的两个不相等实数根.
请根据上述材料解决下面问题:
已知一元二次方程的两根分别为,,则 ______, ______.
已知实数,满足:,,则 ______.
已知实数、、满足:,,且,求的取值范围.
设实数,分别满足,,且,求的值.
20.本小题分
垂美四边形定义如下:对角线互相垂直的四边形叫做“垂美四边形”.
如图,四边形是“垂美四边形”,猜想、与、之间的数量关系:______,并说明理由.
如图,分别以的直角边和斜边为边向外作正方形和正方形,连接、,若,求的长.
如图,在中,,点是外一点,连接,,已知,若以、、、为顶点的四边形为垂美四边形,请直接写出的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.且
13.
14.解:解不等式得,,
解不等式得,,
所以不等式组的解集为:.
,
,
则或,
所以,.
15.解:原式
,
且且,
在,,,中只能取,
当时,原式.
16.如图,即为所求.
如图,即为所求.
.
如图:的坐标为或或时,以、、、四个点为顶点的四边形是平行四边形,
在第二象限,
.
17.解:添加:答案不唯一.
理由:,,
四边形是平行四边形,
,
,
四边形是矩形;
由可知,四边形是矩形,
,
四边形是平行四边形,
,
,
,
,
四边形的面积.
18.解:设每个足球的进价是元,则每个排球的进价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
,
答:每个足球的进价是元,每个排球的进价是元;
设购进足球个,则购进排球个,
由题意得:,
解得:,
又为正整数,
,,,,,,
该商场有种进货方案.
19.;;
;
实数、、满足:,
,是方程的解,
,,
,
,,
,
,
;
,,
,
,
,
是方程的解,
,
,,
.
20.;
解:如图,
四边形,是正方形,为直角三角形,
,,,
,
≌,
,
,
,
,
,
,
四边形为“垂美四边形”,
,
在中,由勾股定理得,,
,同理可求,,
,
解得;
当时,则,
在中,由勾股定理得,,
,
解得:舍负,
,
过点作延长线的垂线,垂足为点,
由题意得,,
,
,
而,,
≌,
,,
,
在中,由勾股定理得,
;
当时,
同上可求此时,,
过点作于点,
同上可证≌,
,,
,
在中,由勾股定理得,,
综上所述,或.
第1页,共1页
同课章节目录
