1.8三角函数的简单应用——2024-2025学年高一数学北师大版2019必修第二册同步课时训练(含解析)
文档属性
| 名称 | 1.8三角函数的简单应用——2024-2025学年高一数学北师大版2019必修第二册同步课时训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 483.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览



文档简介
1.8 三角函数的简单应用——2024-2025学年高一数学北师大版2019必修第二册同步课时训练
一、选择题
1.智能主动降噪耳机工作的原理:通过耳机两端的噪声采集器采集周围的噪音,然后通过听感主动降噪芯片生成相等的反向波抵消噪音(如图).已知噪音的声波曲线(,,)的振幅为1,周期为,初相为0,则通过挺感主动降噪芯片生成相等的反向波曲线为( )
A. B. C. D.
2.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置.若初始位置为,当秒针从(注:此时)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为( )
A. B.
C. D.
3.函数,的图象与直线有且仅有两个不同的交点,则k的取值范围是( )
A. B. C. D.
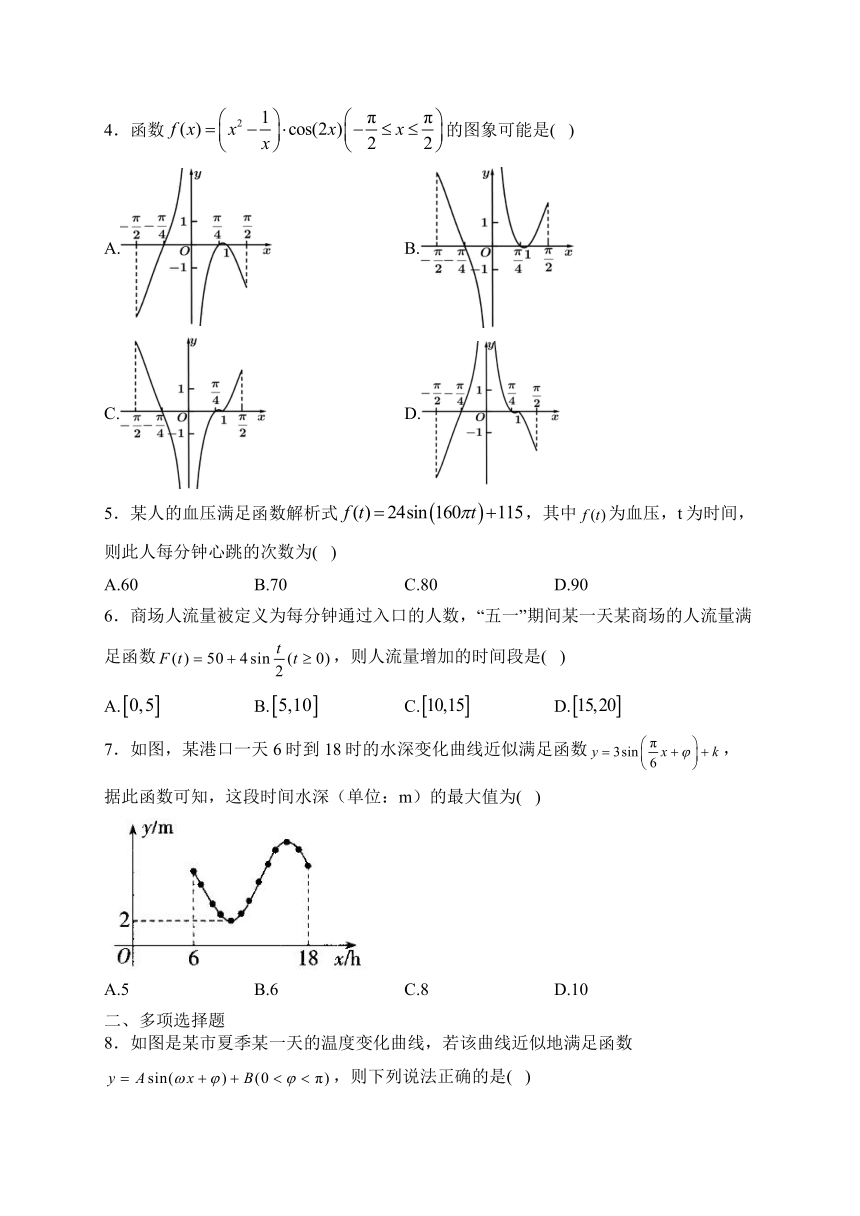
4.函数的图象可能是( )
A. B.
C. D.
5.某人的血压满足函数解析式,其中为血压,t为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
6.商场人流量被定义为每分钟通过入口的人数,“五一”期间某一天某商场的人流量满足函数,则人流量增加的时间段是( )
A. B. C. D.
7.如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
二、多项选择题
8.如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数,则下列说法正确的是( )
A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
三、填空题
9.某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间时,点A与钟面上标12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则__________,其中.
10.如图,某地一天从6时到14时的温度变化曲线近似满足函数,则8时的温度大约为________℃(精确到1℃).
11.如图所示的图象显示的是相对平均海平面的某海湾的水面高度在某天24小时内的变化情况,则水面高度y关于从夜间0时开始的时间x的函数关系式为_________,.
四、解答题
12.已知函数.
(1)若,先列表,然后在方格纸中画出的图象,并写出的单调递减区间;
(2)若,写出不等式的解集(不要求写求解过程).
13.如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数(,,,)的图象,图象的最高点为,且,垂足为点F.
(1)求函数的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE(阴影部分),点P在曲线OD上,其横坐标为,点E在OC上,求儿童乐园的面积.
参考答案
1.答案:C
解析:由某噪音的声波曲线(,,)的振幅为1,周期为,初相为0,
知声波曲线:,
通过听感主动降躁芯片生成相等的反向波曲线为.
故选:C.
2.答案:C
解析:由题意可得,初始位置为,不妨设初相为,
故可得,,则.排除B、D.
又函数周期是60(秒)且秒针按顺时针旋转,即,
所以,即,
故满足题意的函数解析式为:.
故选:C.
3.答案:B
解析:因为时,,则,
因为时,,则,
故,
作出函数图象:
数形结合即可得到,
故选:B.
4.答案:A
解析:,故BC错误;
,故D错误,
故选:A.
5.答案:C
解析:由题意得:函数的周期为,
所以频率,
所以此人每分钟心跳的次数为80.
故选:C.
6.答案:C
解析:由,,知函数的单调递增区间为,.当时,,而,故选C.
7.答案:C
解析:由题图易得,则,.
8.答案:AB
解析:对于A选项,由图象可知,该函数的最小正周期为,A选项正确;
对于B选项,该函数在取得最大值,所以,该函数图象的一条对称轴是直线,B选项正确;
对于C选项,由图象可得,解得,,
图象经过点,,.
,,则,,
所以,函数解析式为,C选项错误;
这一天的函数关系式不一定适用于第二天,要具体情况具体分析,所以,D选项错误.
故选:AB.
9.答案:
解析:函数解析式为,
由题意易知,
当时,,得;
当时,,
可得,所以,
故答案为:.
10.答案:13
解析:由图像可得,,,
,
.
图像最低点的坐标为,
,得,
于是,
.取,
.
当时,.
故答案为:13.
11.答案:
解析:将题图图象看成,的图象,由图象知,,,.将点看成函数图象的第一个特殊点,则,.函数关系式为.
12.答案:(1)答案见解析
(2),
解析:(1)列表如下:
0
x
-1 -2 0 2 0 -1
则函数在区间上的图象如图所示.
当时,的单调递减区间为,.
(2)当时,不等式的解集为,.
13、
(1)答案:
解析:由题,可知,,
将代入,
得,即.
又,,
.
(2)答案:
解析:在中,令,得,
从而得曲线OD的方程为,则,
矩形PMFE的面积,即儿童乐园的面积为.
一、选择题
1.智能主动降噪耳机工作的原理:通过耳机两端的噪声采集器采集周围的噪音,然后通过听感主动降噪芯片生成相等的反向波抵消噪音(如图).已知噪音的声波曲线(,,)的振幅为1,周期为,初相为0,则通过挺感主动降噪芯片生成相等的反向波曲线为( )
A. B. C. D.
2.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置.若初始位置为,当秒针从(注:此时)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为( )
A. B.
C. D.
3.函数,的图象与直线有且仅有两个不同的交点,则k的取值范围是( )
A. B. C. D.
4.函数的图象可能是( )
A. B.
C. D.
5.某人的血压满足函数解析式,其中为血压,t为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
6.商场人流量被定义为每分钟通过入口的人数,“五一”期间某一天某商场的人流量满足函数,则人流量增加的时间段是( )
A. B. C. D.
7.如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
二、多项选择题
8.如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数,则下列说法正确的是( )
A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
三、填空题
9.某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间时,点A与钟面上标12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则__________,其中.
10.如图,某地一天从6时到14时的温度变化曲线近似满足函数,则8时的温度大约为________℃(精确到1℃).
11.如图所示的图象显示的是相对平均海平面的某海湾的水面高度在某天24小时内的变化情况,则水面高度y关于从夜间0时开始的时间x的函数关系式为_________,.
四、解答题
12.已知函数.
(1)若,先列表,然后在方格纸中画出的图象,并写出的单调递减区间;
(2)若,写出不等式的解集(不要求写求解过程).
13.如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数(,,,)的图象,图象的最高点为,且,垂足为点F.
(1)求函数的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE(阴影部分),点P在曲线OD上,其横坐标为,点E在OC上,求儿童乐园的面积.
参考答案
1.答案:C
解析:由某噪音的声波曲线(,,)的振幅为1,周期为,初相为0,
知声波曲线:,
通过听感主动降躁芯片生成相等的反向波曲线为.
故选:C.
2.答案:C
解析:由题意可得,初始位置为,不妨设初相为,
故可得,,则.排除B、D.
又函数周期是60(秒)且秒针按顺时针旋转,即,
所以,即,
故满足题意的函数解析式为:.
故选:C.
3.答案:B
解析:因为时,,则,
因为时,,则,
故,
作出函数图象:
数形结合即可得到,
故选:B.
4.答案:A
解析:,故BC错误;
,故D错误,
故选:A.
5.答案:C
解析:由题意得:函数的周期为,
所以频率,
所以此人每分钟心跳的次数为80.
故选:C.
6.答案:C
解析:由,,知函数的单调递增区间为,.当时,,而,故选C.
7.答案:C
解析:由题图易得,则,.
8.答案:AB
解析:对于A选项,由图象可知,该函数的最小正周期为,A选项正确;
对于B选项,该函数在取得最大值,所以,该函数图象的一条对称轴是直线,B选项正确;
对于C选项,由图象可得,解得,,
图象经过点,,.
,,则,,
所以,函数解析式为,C选项错误;
这一天的函数关系式不一定适用于第二天,要具体情况具体分析,所以,D选项错误.
故选:AB.
9.答案:
解析:函数解析式为,
由题意易知,
当时,,得;
当时,,
可得,所以,
故答案为:.
10.答案:13
解析:由图像可得,,,
,
.
图像最低点的坐标为,
,得,
于是,
.取,
.
当时,.
故答案为:13.
11.答案:
解析:将题图图象看成,的图象,由图象知,,,.将点看成函数图象的第一个特殊点,则,.函数关系式为.
12.答案:(1)答案见解析
(2),
解析:(1)列表如下:
0
x
-1 -2 0 2 0 -1
则函数在区间上的图象如图所示.
当时,的单调递减区间为,.
(2)当时,不等式的解集为,.
13、
(1)答案:
解析:由题,可知,,
将代入,
得,即.
又,,
.
(2)答案:
解析:在中,令,得,
从而得曲线OD的方程为,则,
矩形PMFE的面积,即儿童乐园的面积为.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
