湖南省衡阳市第二十六中学2015-2016学年高一上学期期末考试数学试题
文档属性
| 名称 | 湖南省衡阳市第二十六中学2015-2016学年高一上学期期末考试数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-02 00:00:00 | ||
图片预览
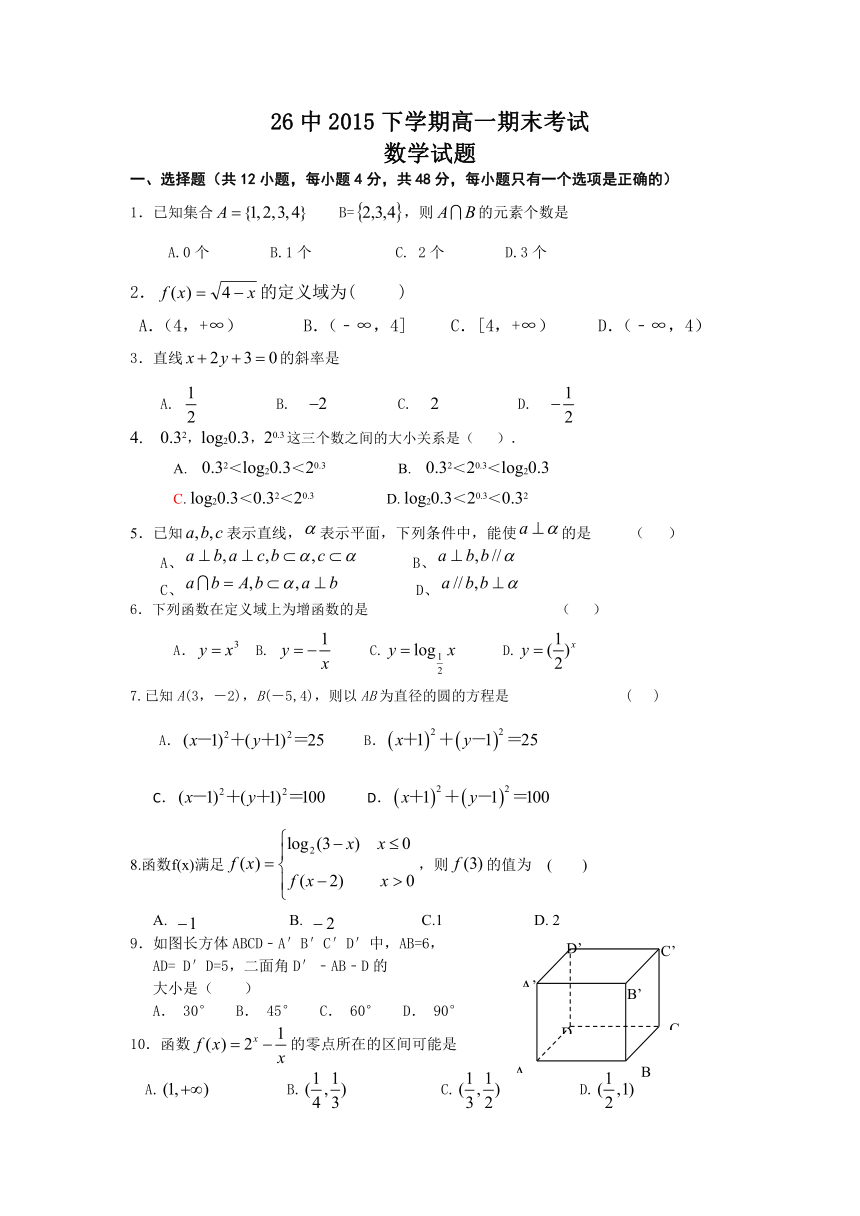

文档简介
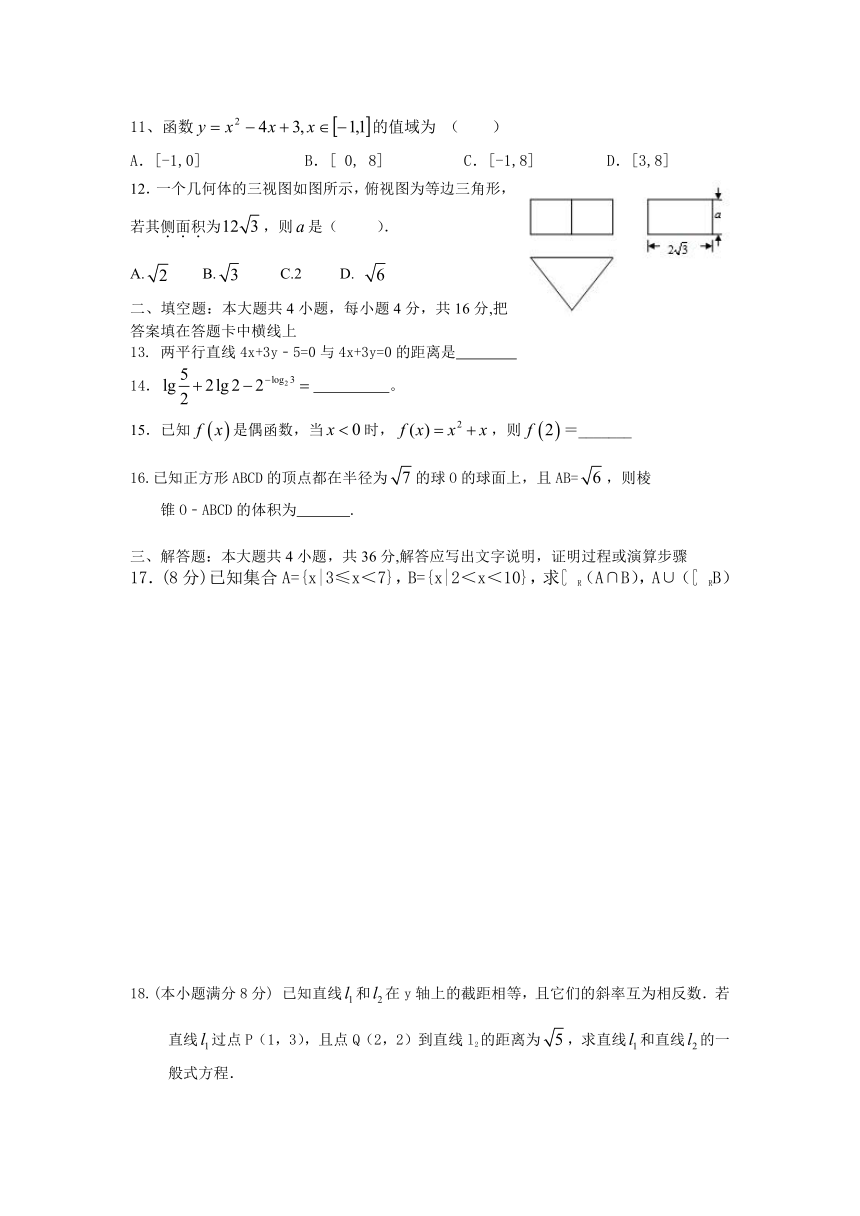
26中2015下学期高一期末考试
数学试题
一、选择题(共12小题,每小题4分,共48分,每小题只有一个选项是正确的)
1.已知集合 B=,则的元素个数是
A.0个 B.1个 C. 2个 D.3个
2.的定义域为( )
A.(4,+∞) B.(﹣∞,4] C.[4,+∞) D.(﹣∞,4)
3.直线的斜率是
A. B. C. D.
4. 0.32,log20.3,20.3这三个数之间的大小关系是( ).
A. 0.32<log20.3<20.3 B. 0.32<20.3<log20.3
C. log20.3<0.32<20.3 D. log20.3<20.3<0.32
5.已知表示直线,表示平面,下列条件中,能使的是 ( )
A、 B、
C、 D、
6.下列函数在定义域上为增函数的是 ( )
A. B. C. D.
7.已知A(3,-2),B(-5,4),则以AB为直径的圆的方程是 ( )
A. B.
C. D.
8.函数f(x)满足,则的值为 ( )
A. B. C.1 D. 2
9.如图长方体ABCD﹣A′B′C′D′中,AB=6,
AD= D′D=5,二面角D′﹣AB﹣D的
大小是( )
A. 30° B. 45° C. 60° D. 90°
10.函数的零点所在的区间可能是
A. B. C. D.
11、函数的值域为 ( )
A.[-1,0] B.[ 0, 8] C.[-1,8] D.[3,8]
12.一个几何体的三视图如图所示,俯视图为等边三角形,若其侧面积为,则是( ).
A. B. C.2 D.
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡中横线上
13. 两平行直线4x+3y﹣5=0与4x+3y=0的距离是
14. 。
15.已知是偶函数,当时,,则=_______
16.已知正方形ABCD的顶点都在半径为的球O的球面上,且AB=,则棱
锥O﹣ABCD的体积为 .
三、解答题:本大题共4小题,共36分,解答应写出文字说明,证明过程或演算步骤
17.(8分)已知集合A={x|3≤x<7},B={x|2<x<10},求 R(A∩B),A∪( RB)
18.(本小题满分8分) 已知直线和在y轴上的截距相等,且它们的斜率互为相反数.若直线过点P(1,3),且点Q(2,2)到直线l2的距离为,求直线和直线的一般式方程.
19.. 如图,在三棱锥中,平面平面,,,分别为,的中点.
(I)求证:平面;
(II)求证:平面平面;
20. (本小题满分10分)圆C过点A(6,4),B(1,),且圆心在直线上.
(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D B D C D A B D B D B C
二、填空题: 13. 1 14. 15. 2 16. 4
三、解答题:
17.解: A∩B
R(A∩B)
( RB)
A∪( RB)
18.解:设直线l1:y=kx+b,直线l2:y=-kx+b----------2分
∵l1过P(1,3)点且Q(2,2)到l2的距离为,
∴--------------------4分
解之得 ----------------6分
故l1:2x-y+1=0 l2:2x+y﹣1=0;或l1:x+2y-7=0 l2:x-2y+7=0----------8分
19..【答案】(I)为中点,∥,面,面,
所以∥面 5分
(Ⅱ)因为,为的中点,
所以.又因为平面平面,且平面,
所以平面.所以平面平面. 10分
20.解:(1)解法1:直线AB的斜率,
所以AB的垂直平分线m的斜率为.
AB的中点的横坐标和纵坐标分别为 .
因此,直线m的方程为.即.-------------2分
又圆心在直线l上,所以圆心是直线m与直线l的交点。联立方程组
解得 ---------------4分
所以圆心坐标为C(3,2),又半径,
则所求圆的方程是---------------------5分
解法2:设所求圆的方程为.由题意得
----------2分
解得 --------------4分
所以所求圆的方程是. ---------------------5分
(2)设线段PQ的中点M(x,y),P
M为线段PQ的中点,则 , 解得 --------------7分
代入圆C中得--------------9分
即线段PQ中点M的轨迹方程为. -----------10分
A
B
C
D
A’
D’
C’
B’
数学试题
一、选择题(共12小题,每小题4分,共48分,每小题只有一个选项是正确的)
1.已知集合 B=,则的元素个数是
A.0个 B.1个 C. 2个 D.3个
2.的定义域为( )
A.(4,+∞) B.(﹣∞,4] C.[4,+∞) D.(﹣∞,4)
3.直线的斜率是
A. B. C. D.
4. 0.32,log20.3,20.3这三个数之间的大小关系是( ).
A. 0.32<log20.3<20.3 B. 0.32<20.3<log20.3
C. log20.3<0.32<20.3 D. log20.3<20.3<0.32
5.已知表示直线,表示平面,下列条件中,能使的是 ( )
A、 B、
C、 D、
6.下列函数在定义域上为增函数的是 ( )
A. B. C. D.
7.已知A(3,-2),B(-5,4),则以AB为直径的圆的方程是 ( )
A. B.
C. D.
8.函数f(x)满足,则的值为 ( )
A. B. C.1 D. 2
9.如图长方体ABCD﹣A′B′C′D′中,AB=6,
AD= D′D=5,二面角D′﹣AB﹣D的
大小是( )
A. 30° B. 45° C. 60° D. 90°
10.函数的零点所在的区间可能是
A. B. C. D.
11、函数的值域为 ( )
A.[-1,0] B.[ 0, 8] C.[-1,8] D.[3,8]
12.一个几何体的三视图如图所示,俯视图为等边三角形,若其侧面积为,则是( ).
A. B. C.2 D.
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡中横线上
13. 两平行直线4x+3y﹣5=0与4x+3y=0的距离是
14. 。
15.已知是偶函数,当时,,则=_______
16.已知正方形ABCD的顶点都在半径为的球O的球面上,且AB=,则棱
锥O﹣ABCD的体积为 .
三、解答题:本大题共4小题,共36分,解答应写出文字说明,证明过程或演算步骤
17.(8分)已知集合A={x|3≤x<7},B={x|2<x<10},求 R(A∩B),A∪( RB)
18.(本小题满分8分) 已知直线和在y轴上的截距相等,且它们的斜率互为相反数.若直线过点P(1,3),且点Q(2,2)到直线l2的距离为,求直线和直线的一般式方程.
19.. 如图,在三棱锥中,平面平面,,,分别为,的中点.
(I)求证:平面;
(II)求证:平面平面;
20. (本小题满分10分)圆C过点A(6,4),B(1,),且圆心在直线上.
(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D B D C D A B D B D B C
二、填空题: 13. 1 14. 15. 2 16. 4
三、解答题:
17.解: A∩B
R(A∩B)
( RB)
A∪( RB)
18.解:设直线l1:y=kx+b,直线l2:y=-kx+b----------2分
∵l1过P(1,3)点且Q(2,2)到l2的距离为,
∴--------------------4分
解之得 ----------------6分
故l1:2x-y+1=0 l2:2x+y﹣1=0;或l1:x+2y-7=0 l2:x-2y+7=0----------8分
19..【答案】(I)为中点,∥,面,面,
所以∥面 5分
(Ⅱ)因为,为的中点,
所以.又因为平面平面,且平面,
所以平面.所以平面平面. 10分
20.解:(1)解法1:直线AB的斜率,
所以AB的垂直平分线m的斜率为.
AB的中点的横坐标和纵坐标分别为 .
因此,直线m的方程为.即.-------------2分
又圆心在直线l上,所以圆心是直线m与直线l的交点。联立方程组
解得 ---------------4分
所以圆心坐标为C(3,2),又半径,
则所求圆的方程是---------------------5分
解法2:设所求圆的方程为.由题意得
----------2分
解得 --------------4分
所以所求圆的方程是. ---------------------5分
(2)设线段PQ的中点M(x,y),P
M为线段PQ的中点,则 , 解得 --------------7分
代入圆C中得--------------9分
即线段PQ中点M的轨迹方程为. -----------10分
A
B
C
D
A’
D’
C’
B’
同课章节目录
