2024~2025学年人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线同步练习(无答案)
文档属性
| 名称 | 2024~2025学年人教版数学八年级上册 11.1.2 三角形的高、中线与角平分线同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 355.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览


文档简介
11.1.2三角形的高、中线与角平分线
一、单选题
1.能把三角形面积两等分的是三角形的( )
A.中线 B.高线
C.角平分线 D.两边中点连线
2.如图,在中,是高,是角平分线,是中线.则下列结论错误的是( )
A. B. C. D.
3.在学完八上三角形一章后,某班组织了一次数学活动课,老师让同学们自己谈谈对三角形相关知识的理解小峰说:“存在这样的三角形,它的三条高之比可以为::,::,::,::”老师说有一个三角形是不存在的,你认为不存在的三角形是( )
A.:: B.:: C.:: D.::
4.如图,中,D是中点,是的中线,,则等于( )
A.10 B.8 C.6 D.4
5.如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离为3.8,则BC的长为( )
A.3.8 B.7.6 C.11.4 D.11.2
6.一个三角形的三条角平分线的交点在( )
A.三角形内 B.三角形外
C.三角形的某边上 D.以上三种情形都有可能
7.如图,是的中线,则下列结论正确的是( )
A. B.
C. D.
8.已知△ABC中,D是BC边上的一点,点E在AD上,下列结论中不一定成立的是( )
A.如果AD是△ABC的中线,那么ED是△EBC的中线
B.如果AD是△ABC的高,那么ED是△EBC的高
C.如果AD是△ABC的角平分线,那么ED是△EBC的角平分线
D.如果AD是△ABC的高,那么BD是△ABE的高
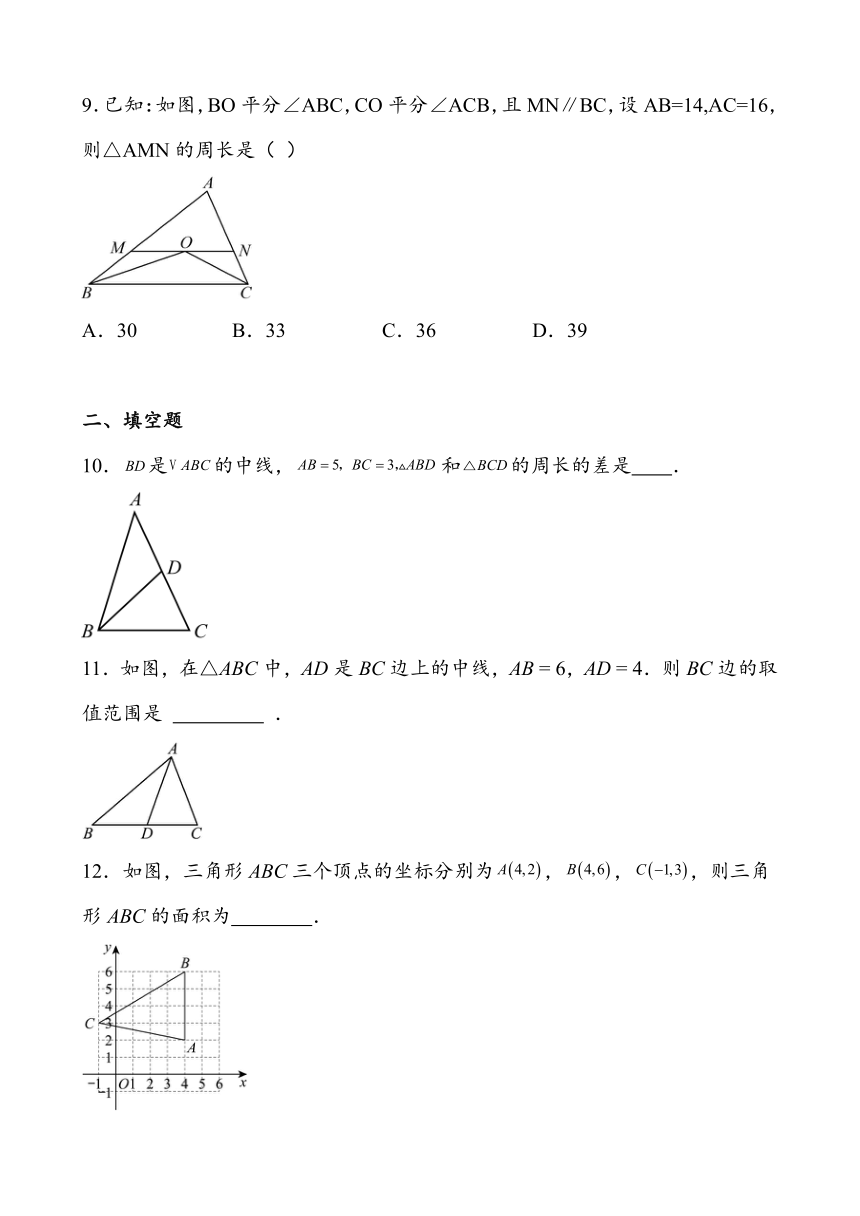
9.已知:如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=14,AC=16,则△AMN的周长是( )
A.30 B.33 C.36 D.39
二、填空题
10.是的中线,和的周长的差是 .
11.如图,在△ABC中,AD是BC边上的中线,AB = 6,AD = 4.则BC边的取值范围是 .
12.如图,三角形ABC三个顶点的坐标分别为,,,则三角形ABC的面积为 .
13.一个三角形的底是3分米,高是4分米,它的面积是 平方分米.
14.如图,在中,D、E、F分别为的中点,且,则的面积是 .
15.在中,D是边的中点,,若的面积为12,则的面积为 .
三、解答题
16.如图,中,,D为的中点,的周长比的周长大2,且的边长是方程的解,求三边的长.
17.如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个,它的三个顶点均与小正方形的顶点重合.
(1)将向右平移3个单位长度,得到(与与与对应),请在方格纸中画出;
(2)在(1)的条件下;连接和,请求出的面积.
18.如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,
(1)在图中画出平移后的△A′B′C′;
(2)画出AB边上的高CE;
(3)过点A画BC的平行线;
(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有 个.(注:格点指网格线的交点)
19.在三角形中,是边上的中线,,,求与的周长之差.
20.如图,边长为1个单位长度的小正方形组成的方格纸中,的顶点都在方格纸的格点上.
(1)将向右平移4个单位,再向上平移5个单位得到,请画出;
(2)的面积为 .
(3)在图中找一个格点,使
21.如图,三角形是由三角形经过某种平移得到的,点A与点,点B与点,点C与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的;
(2)若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为,分别求a和b的值;
(3)直接写出三角形的面积为__________.
一、单选题
1.能把三角形面积两等分的是三角形的( )
A.中线 B.高线
C.角平分线 D.两边中点连线
2.如图,在中,是高,是角平分线,是中线.则下列结论错误的是( )
A. B. C. D.
3.在学完八上三角形一章后,某班组织了一次数学活动课,老师让同学们自己谈谈对三角形相关知识的理解小峰说:“存在这样的三角形,它的三条高之比可以为::,::,::,::”老师说有一个三角形是不存在的,你认为不存在的三角形是( )
A.:: B.:: C.:: D.::
4.如图,中,D是中点,是的中线,,则等于( )
A.10 B.8 C.6 D.4
5.如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离为3.8,则BC的长为( )
A.3.8 B.7.6 C.11.4 D.11.2
6.一个三角形的三条角平分线的交点在( )
A.三角形内 B.三角形外
C.三角形的某边上 D.以上三种情形都有可能
7.如图,是的中线,则下列结论正确的是( )
A. B.
C. D.
8.已知△ABC中,D是BC边上的一点,点E在AD上,下列结论中不一定成立的是( )
A.如果AD是△ABC的中线,那么ED是△EBC的中线
B.如果AD是△ABC的高,那么ED是△EBC的高
C.如果AD是△ABC的角平分线,那么ED是△EBC的角平分线
D.如果AD是△ABC的高,那么BD是△ABE的高
9.已知:如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=14,AC=16,则△AMN的周长是( )
A.30 B.33 C.36 D.39
二、填空题
10.是的中线,和的周长的差是 .
11.如图,在△ABC中,AD是BC边上的中线,AB = 6,AD = 4.则BC边的取值范围是 .
12.如图,三角形ABC三个顶点的坐标分别为,,,则三角形ABC的面积为 .
13.一个三角形的底是3分米,高是4分米,它的面积是 平方分米.
14.如图,在中,D、E、F分别为的中点,且,则的面积是 .
15.在中,D是边的中点,,若的面积为12,则的面积为 .
三、解答题
16.如图,中,,D为的中点,的周长比的周长大2,且的边长是方程的解,求三边的长.
17.如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个,它的三个顶点均与小正方形的顶点重合.
(1)将向右平移3个单位长度,得到(与与与对应),请在方格纸中画出;
(2)在(1)的条件下;连接和,请求出的面积.
18.如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,
(1)在图中画出平移后的△A′B′C′;
(2)画出AB边上的高CE;
(3)过点A画BC的平行线;
(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有 个.(注:格点指网格线的交点)
19.在三角形中,是边上的中线,,,求与的周长之差.
20.如图,边长为1个单位长度的小正方形组成的方格纸中,的顶点都在方格纸的格点上.
(1)将向右平移4个单位,再向上平移5个单位得到,请画出;
(2)的面积为 .
(3)在图中找一个格点,使
21.如图,三角形是由三角形经过某种平移得到的,点A与点,点B与点,点C与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
(1)分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的;
(2)若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为,分别求a和b的值;
(3)直接写出三角形的面积为__________.
