第十一章 三角形 单元试卷 (含答案)人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 单元试卷 (含答案)人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 576.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览


文档简介
第十一章 三角形 单元试卷
一、单选题
1.如图,铜陵长江大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是( )
A.三角形的不稳定性 B.三角形的稳定性
C.四边形的不稳定性 D.四边形的稳定性
2.如图,在中,是上的一点,且与的面积相等,则线段为的
A.高 B.角平分线 C.中线 D.不能确定
3.如图所示,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,FC⊥BC于点C,下列说法错误的是( )
A.FC是△ABC的AB边上的高 B.BE是△ABC的AC边上的高
C.AD是△ABC的BC边上的高 D.BC不是△ABC的高
4.下列说法不正确的是( )
A.三角形的三条高线交于一点 B.直角三角形有三条高
C.三角形的三条角平分线交于一点 D.三角形的三条中线交于一点
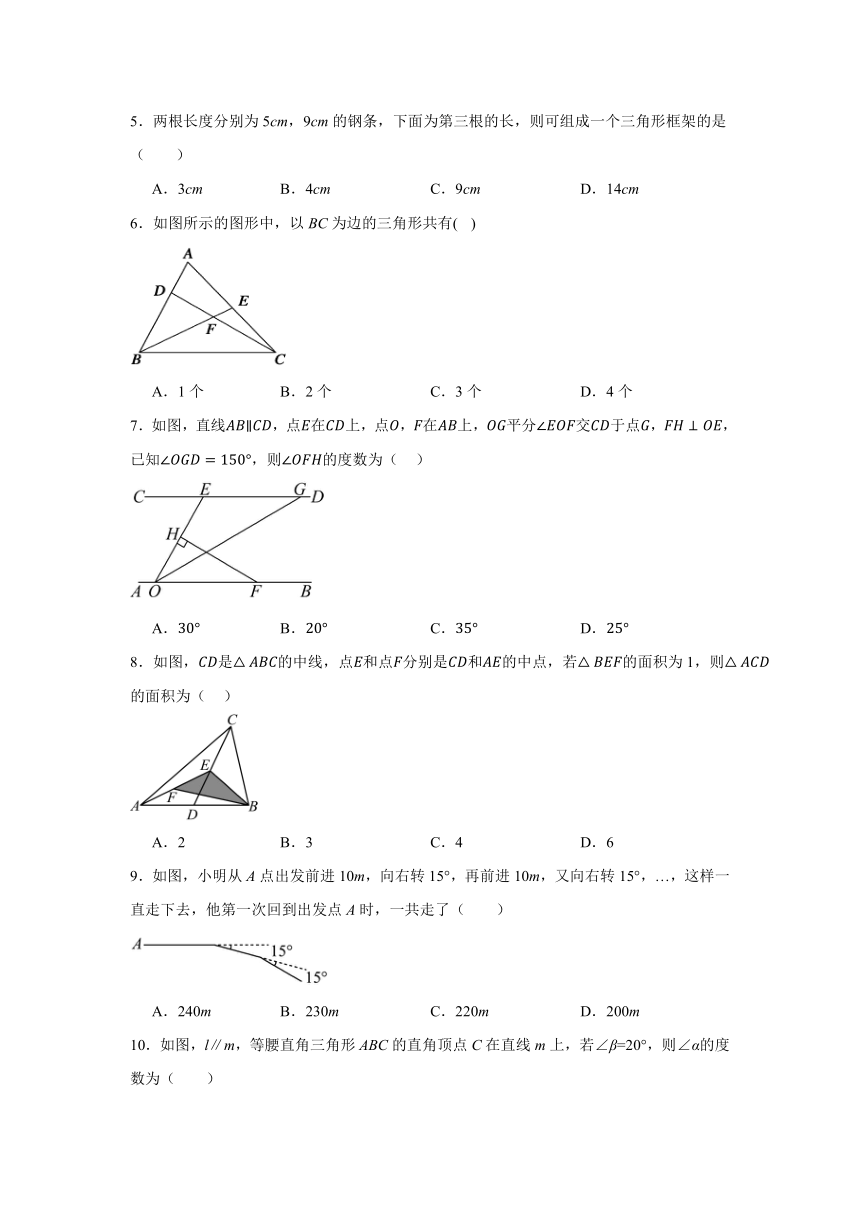
5.两根长度分别为5cm,9cm的钢条,下面为第三根的长,则可组成一个三角形框架的是( )
A.3cm B.4cm C.9cm D.14cm
6.如图所示的图形中,以BC为边的三角形共有( )
A.1个 B.2个 C.3个 D.4个
7.如图,直线,点在上,点,在上,平分交于点,,已知,则的度数为( )
A. B. C. D.
8.如图,是的中线,点和点分别是和的中点,若的面积为1,则的面积为( )
A.2 B.3 C.4 D.6
9.如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
A.240m B.230m C.220m D.200m
10.如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
A.25° B.30°
C.20° D.35°
二、填空题
11.如果一个三角形两边为3cm,7cm,且第三边为奇数,则三角形的周长是 .
12.任意一个十边形的内角和为 .
13.如图,在中,已知,则 .
14.如图,是的角平分线,,相交于D,的度数是 .
15.如图,,,和E的平分线交于点,则 .
16.如图,角A等于65度,角B等于75度,将纸片的一角折叠,使点C落在三角形ABC内,则的度数 .
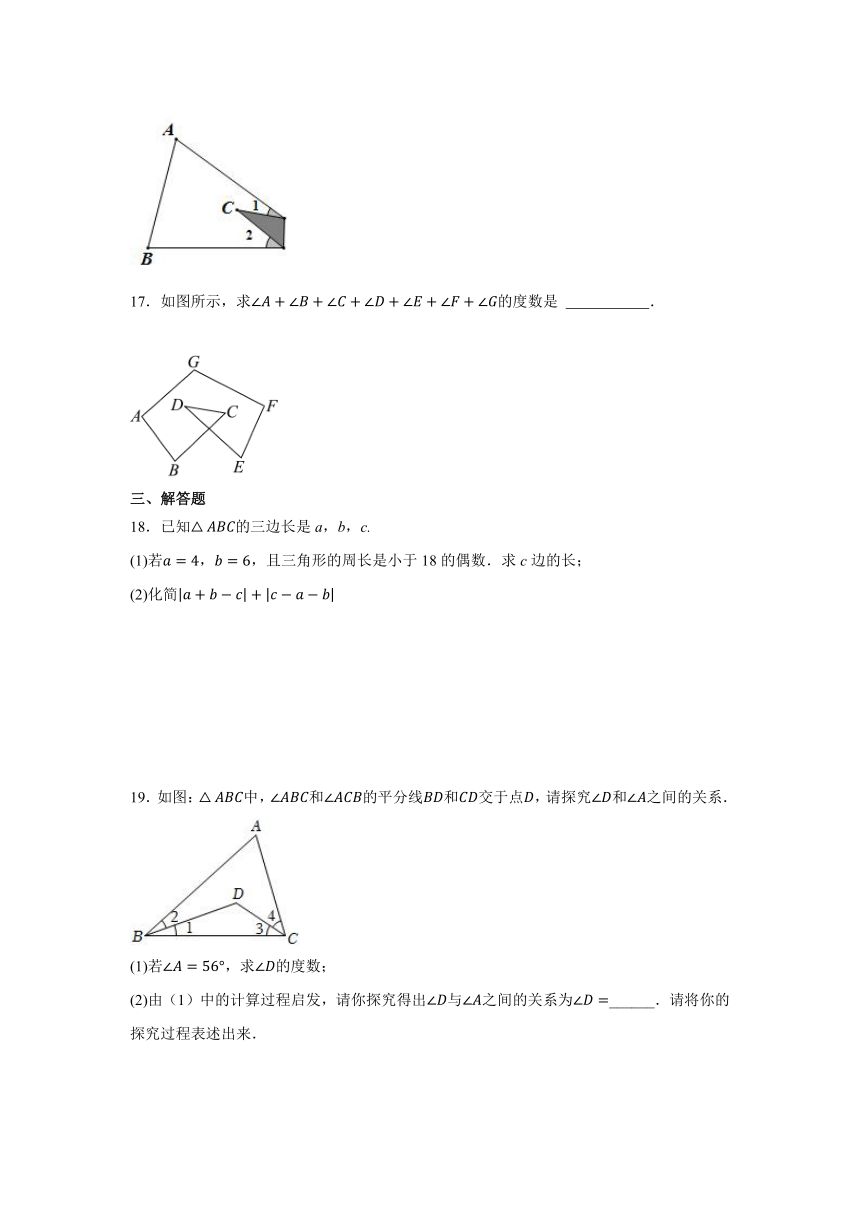
17.如图所示,求的度数是 .
三、解答题
18.已知的三边长是a,b,c.
(1)若,,且三角形的周长是小于18的偶数.求c边的长;
(2)化简
19.如图:中,和的平分线和交于点,请探究和之间的关系.
(1)若,求的度数;
(2)由(1)中的计算过程启发,请你探究得出与之间的关系为______.请将你的探究过程表述出来.
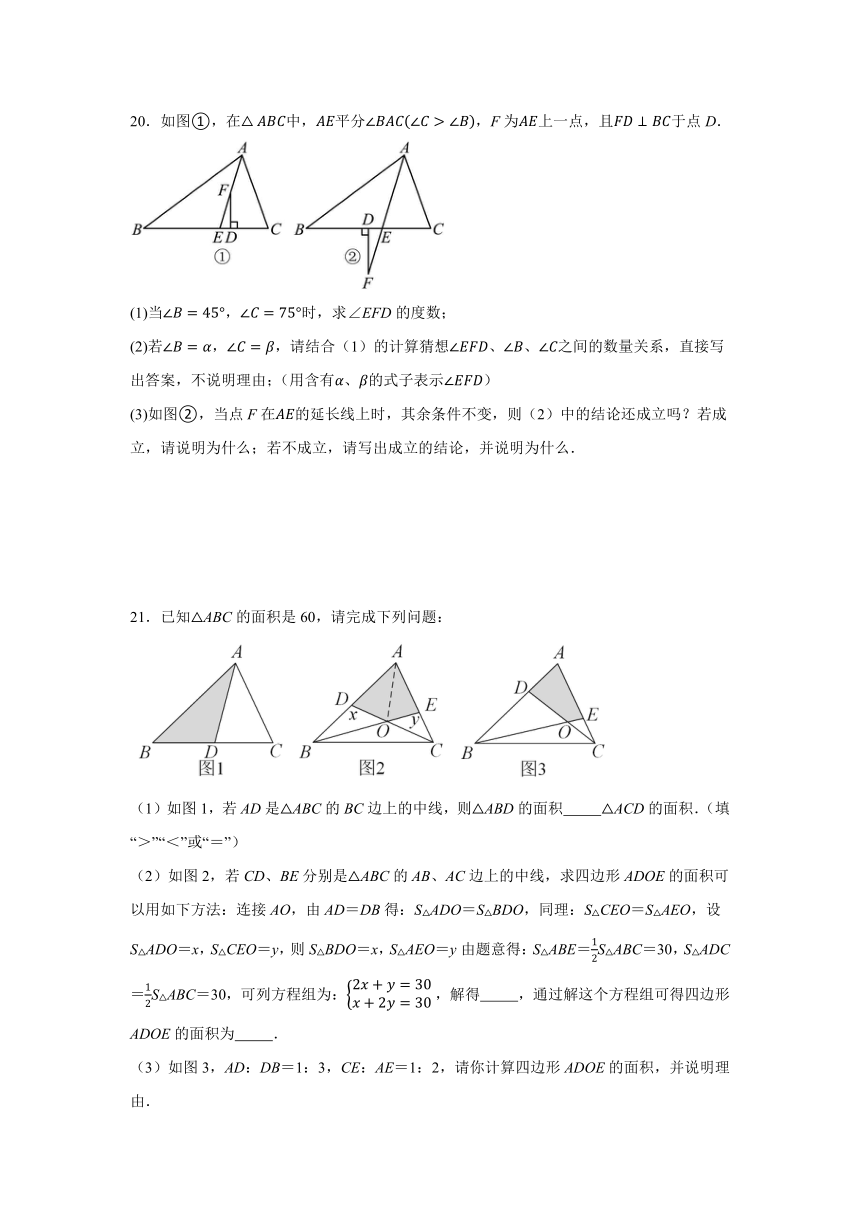
20.如图①,在中,平分,F为上一点,且于点D.
(1)当,时,求∠EFD的度数;
(2)若,,请结合(1)的计算猜想、、之间的数量关系,直接写出答案,不说明理由;(用含有、的式子表示)
(3)如图②,当点F在的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.
21.已知△ABC的面积是60,请完成下列问题:
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积 △ACD的面积.(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=S△ABC=30,S△ADC=S△ABC=30,可列方程组为:,解得 ,通过解这个方程组可得四边形ADOE的面积为 .
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.
22.中,点在边延长线上,的延长线与的角平分线相交于点.
(1)如图1,求证:,
(2)如图2,的角平分线交于,则与之间的数量关系为______,
(3)在(2)的条件下如图3,过点作于,,若,求的度数.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A C D A A A A
11.15cm、17cm、19cm.
12.
13.
14.
15.
16.80°
17.
18.(1)解:∵的三边长是a,b,c,,,
∴,
即,
∵三角形的周长是小于18的偶数,
∴或;
(2)解:∵的三边长是a,b,c,
∴,
∴,,
∴
.
19.(1)解:∵和的平分线交于点,
∴,,
∵,
∴,
∴
,
∴.
∴的度数为.
(2)∵和的平分线交于点,
∴,,
∵,
∴
,
∴
.
20.(1)解:∵,,
∴,
∵平分,
∴,
由三角形的外角性质得,,
∴;
(2)解:,理由如下:
由三角形的内角和定理得,,
∵平分,
∴,
由三角形的外角性质得,,
∵,
∴,
即;
(3)解:结论仍然成立,理由如下:
同(2)可证,
由三角形的内角和定理得,,
∵平分,
∴,
由三角形的外角性质得,,
∴,
∴,
即.
21.解:(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴,,
∴S△ABD=S△ACD,
(2)解方程组得,
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:,20;
(3)如图3,连接AO,
∵AD:DB=1:3,
∴S△ADO=S△BDO,
∵CE:AE=1:2,
∴S△CEO=S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=S△ABC=40,S△ADC=S△ABC=15,
可列方程组为:,
解得:,
∴S四边形ADOE=S△ADO+S△AEO=x+2 y=13.
22.(1)如图1,
∵平分;
∴,
∵,,
∴,
∴;
(2)如图2,
由(1)得:,
∵平分,
∴,
∵,
∴,即有,
∴,
故填:.
(3)如图3,
由,设,,
由,,,
设,
则有,,
设
∵,
∴,
∵,即,解得:,
∴,,,
在,,∴,即,
∴,
∵,
∴
联立 ,解得:,
∴.
一、单选题
1.如图,铜陵长江大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是( )
A.三角形的不稳定性 B.三角形的稳定性
C.四边形的不稳定性 D.四边形的稳定性
2.如图,在中,是上的一点,且与的面积相等,则线段为的
A.高 B.角平分线 C.中线 D.不能确定
3.如图所示,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,FC⊥BC于点C,下列说法错误的是( )
A.FC是△ABC的AB边上的高 B.BE是△ABC的AC边上的高
C.AD是△ABC的BC边上的高 D.BC不是△ABC的高
4.下列说法不正确的是( )
A.三角形的三条高线交于一点 B.直角三角形有三条高
C.三角形的三条角平分线交于一点 D.三角形的三条中线交于一点
5.两根长度分别为5cm,9cm的钢条,下面为第三根的长,则可组成一个三角形框架的是( )
A.3cm B.4cm C.9cm D.14cm
6.如图所示的图形中,以BC为边的三角形共有( )
A.1个 B.2个 C.3个 D.4个
7.如图,直线,点在上,点,在上,平分交于点,,已知,则的度数为( )
A. B. C. D.
8.如图,是的中线,点和点分别是和的中点,若的面积为1,则的面积为( )
A.2 B.3 C.4 D.6
9.如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
A.240m B.230m C.220m D.200m
10.如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
A.25° B.30°
C.20° D.35°
二、填空题
11.如果一个三角形两边为3cm,7cm,且第三边为奇数,则三角形的周长是 .
12.任意一个十边形的内角和为 .
13.如图,在中,已知,则 .
14.如图,是的角平分线,,相交于D,的度数是 .
15.如图,,,和E的平分线交于点,则 .
16.如图,角A等于65度,角B等于75度,将纸片的一角折叠,使点C落在三角形ABC内,则的度数 .
17.如图所示,求的度数是 .
三、解答题
18.已知的三边长是a,b,c.
(1)若,,且三角形的周长是小于18的偶数.求c边的长;
(2)化简
19.如图:中,和的平分线和交于点,请探究和之间的关系.
(1)若,求的度数;
(2)由(1)中的计算过程启发,请你探究得出与之间的关系为______.请将你的探究过程表述出来.
20.如图①,在中,平分,F为上一点,且于点D.
(1)当,时,求∠EFD的度数;
(2)若,,请结合(1)的计算猜想、、之间的数量关系,直接写出答案,不说明理由;(用含有、的式子表示)
(3)如图②,当点F在的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.
21.已知△ABC的面积是60,请完成下列问题:
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积 △ACD的面积.(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=S△ABC=30,S△ADC=S△ABC=30,可列方程组为:,解得 ,通过解这个方程组可得四边形ADOE的面积为 .
(3)如图3,AD:DB=1:3,CE:AE=1:2,请你计算四边形ADOE的面积,并说明理由.
22.中,点在边延长线上,的延长线与的角平分线相交于点.
(1)如图1,求证:,
(2)如图2,的角平分线交于,则与之间的数量关系为______,
(3)在(2)的条件下如图3,过点作于,,若,求的度数.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A C D A A A A
11.15cm、17cm、19cm.
12.
13.
14.
15.
16.80°
17.
18.(1)解:∵的三边长是a,b,c,,,
∴,
即,
∵三角形的周长是小于18的偶数,
∴或;
(2)解:∵的三边长是a,b,c,
∴,
∴,,
∴
.
19.(1)解:∵和的平分线交于点,
∴,,
∵,
∴,
∴
,
∴.
∴的度数为.
(2)∵和的平分线交于点,
∴,,
∵,
∴
,
∴
.
20.(1)解:∵,,
∴,
∵平分,
∴,
由三角形的外角性质得,,
∴;
(2)解:,理由如下:
由三角形的内角和定理得,,
∵平分,
∴,
由三角形的外角性质得,,
∵,
∴,
即;
(3)解:结论仍然成立,理由如下:
同(2)可证,
由三角形的内角和定理得,,
∵平分,
∴,
由三角形的外角性质得,,
∴,
∴,
即.
21.解:(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,
∴,,
∴S△ABD=S△ACD,
(2)解方程组得,
∴S△AOD=S△BOD=10,
∴S四边形ADOB=S△AOD+S△AOE=10+10=20,
故答案为:,20;
(3)如图3,连接AO,
∵AD:DB=1:3,
∴S△ADO=S△BDO,
∵CE:AE=1:2,
∴S△CEO=S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=S△ABC=40,S△ADC=S△ABC=15,
可列方程组为:,
解得:,
∴S四边形ADOE=S△ADO+S△AEO=x+2 y=13.
22.(1)如图1,
∵平分;
∴,
∵,,
∴,
∴;
(2)如图2,
由(1)得:,
∵平分,
∴,
∵,
∴,即有,
∴,
故填:.
(3)如图3,
由,设,,
由,,,
设,
则有,,
设
∵,
∴,
∵,即,解得:,
∴,,,
在,,∴,即,
∴,
∵,
∴
联立 ,解得:,
∴.
