浙教版九年级数学上册数学综合卷(含答案)
文档属性
| 名称 | 浙教版九年级数学上册数学综合卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 389.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 10:21:23 | ||
图片预览


文档简介
浙教版九年级数学上册数学综合
一、单选题
1.将抛物线向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A. B.
C. D.
2.下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图象”是随机事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“概率为0.0001的事件”是不可能事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
3.如图,在△ABC中,DE∥BC,若AD:DB=1:3,DE=4,则BC=( )
A.10 B.12 C.15 D.16
4.抛物线y=﹣x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
A.x<1 B.﹣3<x<1 C.x>1 D.x>﹣3
5.如图,已知AB=AC,∠B<30°,BC上一点D满足∠BAD=120°,=,则的值为( )
A. B. C. D.
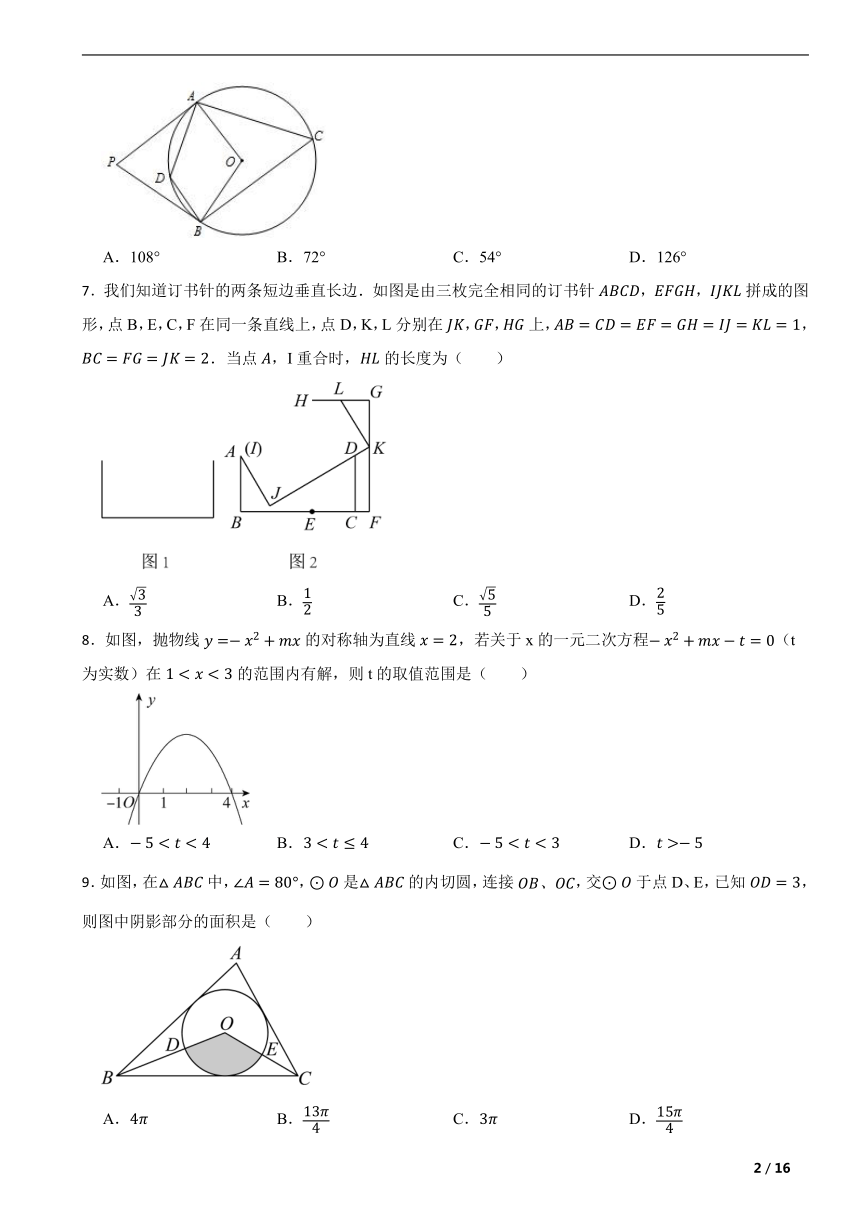
6.如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,点D是劣弧上的一点,则∠ADB=( )
A.108° B.72° C.54° D.126°
7.我们知道订书针的两条短边垂直长边.如图是由三枚完全相同的订书针,,拼成的图形,点B,E,C,F在同一条直线上,点D,K,L分别在,,上,,.当点,I重合时,的长度为( )
A. B. C. D.
8.如图,抛物线的对称轴为直线,若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是( )
A. B. C. D.
9.如图,在中,,是的内切圆,连接,交于点D、E,已知,则图中阴影部分的面积是( )
A. B. C. D.
10.如图,正方形中,点M,N分别为,上的动点,且,,交于点 E,点 F 为 的中点,点P为上一个动点,连接,.若,则 的最小值为( )
A. B. C.5 D.
二、填空题
11.如果函数是二次函数,那么的值是 .
12.现将背面完全相同,正面分别标有数﹣2,﹣1,0,1,2的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的相反数作为点P的纵坐标,则点P落在直线 上方的概率为 .
13.如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为 .
14.已知二次函数(m为常数)的图象与x轴有交点,且当x<-3时,y随x的增大而增大,则m的取值范围是
15.如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8 ,△D′PH的面积是4 ,则矩形ABCD的面积等于 .
16.婆罗摩笈多是公元7世纪的古印度伟大数学家,曾研究对角线互相垂直的圆内接四边形,我们把这类四边形称为“婆罗摩笈多四边形”.如图,四边形是的内接四边形,且是“婆罗摩笈多四边形”、若,则的半径为 .
三、解答题
17.如图所示,在⊙O中直径AB垂直于弦CD,垂足为E,若BE=2 ,CD=6 .求⊙O的半径.
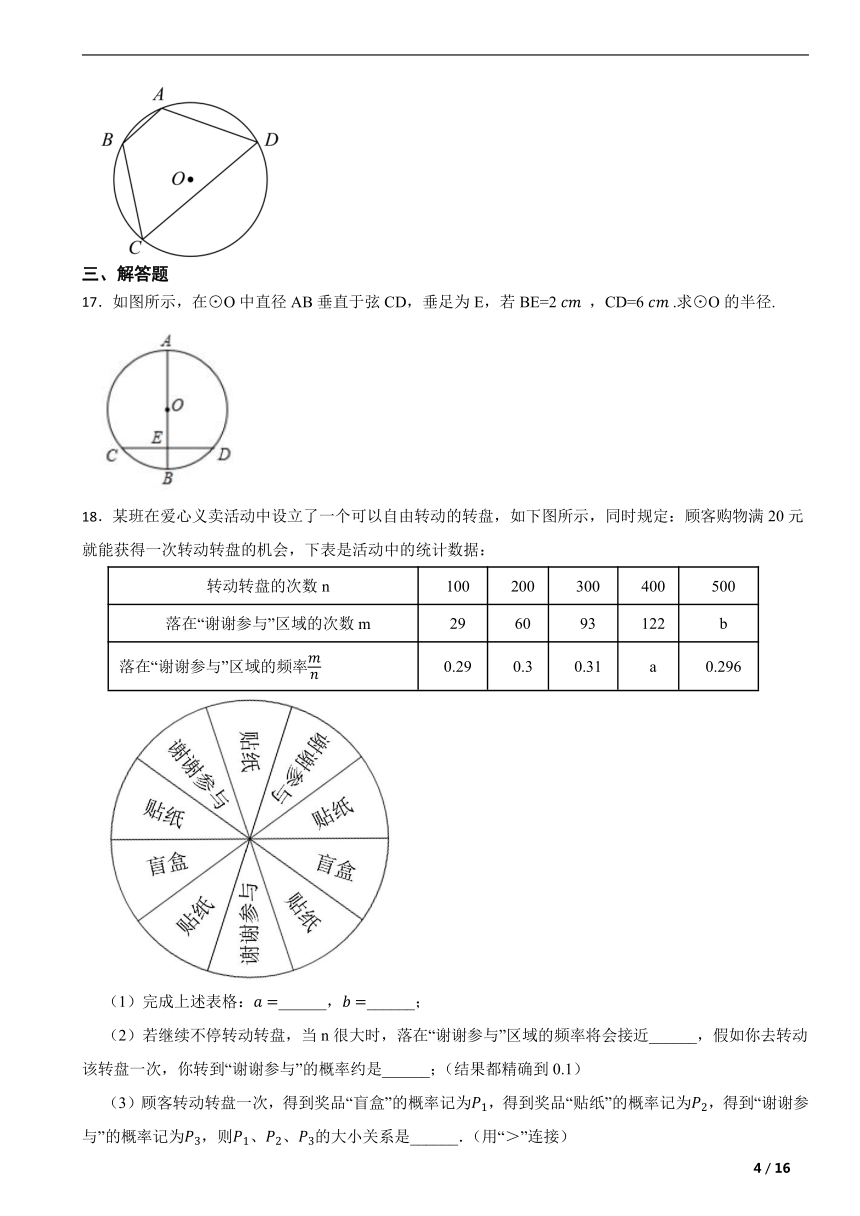
18.某班在爱心义卖活动中设立了一个可以自由转动的转盘,如下图所示,同时规定:顾客购物满20元就能获得一次转动转盘的机会,下表是活动中的统计数据:
转动转盘的次数n 100 200 300 400 500
落在“谢谢参与”区域的次数m 29 60 93 122 b
落在“谢谢参与”区域的频率 0.29 0.3 0.31 a 0.296
(1)完成上述表格:______,______;
(2)若继续不停转动转盘,当n很大时,落在“谢谢参与”区域的频率将会接近______,假如你去转动该转盘一次,你转到“谢谢参与”的概率约是______;(结果都精确到0.1)
(3)顾客转动转盘一次,得到奖品“盲盒”的概率记为,得到奖品“贴纸”的概率记为,得到“谢谢参与”的概率记为,则、、的大小关系是______.(用“>”连接)
19.已知函数 y = kx2 + (k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
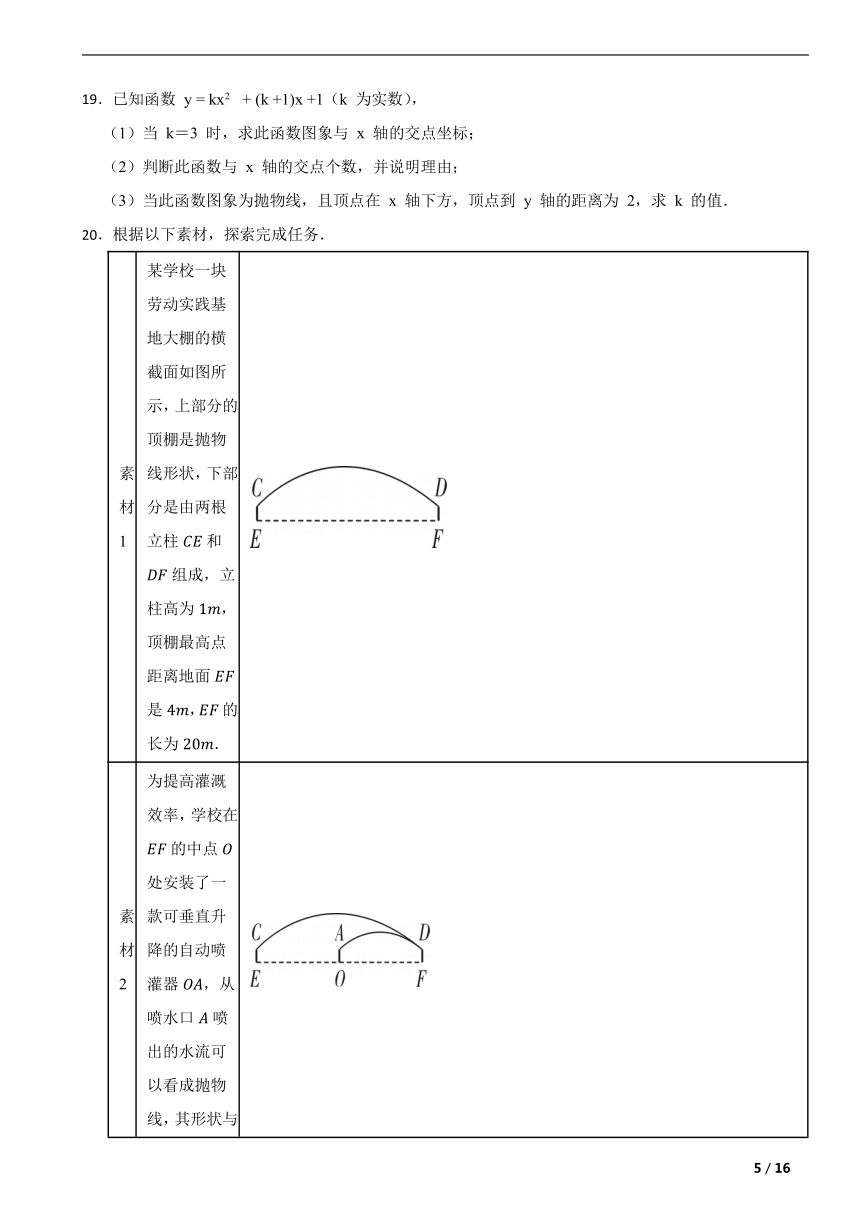
20.根据以下素材,探索完成任务.
素材1 某学校一块劳动实践基地大棚的横截面如图所示,上部分的顶棚是抛物线形状,下部分是由两根立柱和组成,立柱高为,顶棚最高点距离地面是,的长为.
素材2 为提高灌溉效率,学校在的中点处安装了一款可垂直升降的自动喷灌器,从喷水口喷出的水流可以看成抛物线,其形状与的图象相同,,此时水流刚好喷到立柱的端点处.
问题解决
任务1 确定顶棚的形状 以顶棚最高点为坐标原点建立平面直角坐标系,求出顶棚部分抛物线的表达式.
任务2 探索喷水的高度 问处喷出的水流在距离点水平距离为多少米时达到最高.
任务3 调整喷头的高度 如何调整喷水口的高度(形状不变),使水流喷灌时恰好落在边缘处.
21.如图1,四边形内接于,为直径,,,交于点E,,过点O作,垂足为G,交于点H.
(1)求的半径;
(2)当时,求的值;
(3)延长交的延长线于点Q,当时,求的长.
22.阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).
答案解析部分
1.A
2.D
3.D
4.B
5.A
解:如图,作BE∥AC交AD于E,作BH⊥AE于H,
∵AB=AC,
∴∠ABC=∠C,
∵BE∥AC,
∴∠DBE=∠C,
∴∠ABC=∠DBE,
∵∠DBE=∠C,∠ADC=∠EDB,
∴△ADC∽△EDB,
∴,
设AB=AC=6a,
∴BE=14a,
∵∠BAD=120°,BH⊥AE,
∴∠ABH=30°,
∴,,
∴,
在Rt△BEH中,根据勾股定理,得
∵EH2=BE2-BH2,
∴
∴,
即,
解得AD=3a,
则;
6.D
解:∵PA,PB分别与⊙O相切于A,B两点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°-72°=108°,
∴,
∵四边形ADBC是圆内接四边形,
∴∠ACB+∠ADB=180°,
∴∠ADB=180°-∠ACB=180°-54°=126°,
7.B
8.B
9.B
10.B
11.0
12.
13.5
14.
解:二次函数(m为常数)的图象与x轴有交点 ,则令得则解得,又因为当x<-3时,y随x的增大而增大 ,且,函数开口向下,则对称轴直线方程:,综上所述
15.8(3 +2 )
【解答】解:由翻折可知:
∠A=∠A′=90°,∠D=∠D′=90°,
∵∠FPG=90°,
∴∠A′=∠FPG,
∴A′E∥PF,
∴∠A′EP=∠D′PH,
∴△AE′P∽△D′PH,
∴ ,
∵AB=CD,AB=A′P,CD=D′P,
∴A′P=D′P,
∵ ,
∴A′E= D′P,
∴S△A′EP= A′E A′P= × D′P D′P=8 ,
解得D′P=4(负值舍去),
∴A′P=D′P=4,
∴AE=A′E=4 ,
∴EP= ,
∴PH=
DH=D′H= 2 ,
∴AD=AE+EP+PH+DH
=4 +4 +2 +2
=6 +4 +2 .
AB=A′P=4,
∴S矩形ABCD=AB AD
=4(6 +4 +2 )
=8(3 +2 + ).
16.1
17.解: 连接OD,设半径为r,
∵AB⊥CD, ∵CD=6,
∴CE=DE=3,
∵BE=2,∴OE=r-2
∴在Rt△OED中,r =3 +(r-2) ,
解得:r=
18.(1))0.305,148
(2)0.3,0.3
(3)
19.(1)解: ∵k=3 ,∴ y=3x2+4x+1,
令 y=0,∴ 3x2+4x+1=0, 解得:x1=-1,x2=- ,
∴此函数图象与 x 轴的交点坐标为(-1,0),(- ,0).
(2)解:∵y = kx2 + (k +1)x +1,
∴①当 k=0 时,
函数为 y=x+1,
此函数图象与 x 轴有一个公共点;
②当 k≠0 时,
∴△=b2-4ac=(k+1)2-4k=(k-1)2,
若 k=1 则△=0,它的图象与 x 轴有一个公共点;
若 k≠1 则 △>0,它的图象与 x 轴有两个公共点;
∴当 k=0 或 1 时, 它的图象与 x 轴有一个公共点; 当 k≠0 且 k≠1 时,图象与与 x 轴有两个公共点.
(3)解:依题可得:
=2,
解得:k=或k=-,
①当k=时,
∴y=(x+2)2-,
∴顶点坐标为(-2,-),
∴顶点在 x 轴下方,满足题意;
②当k=- 时,
∴y=-(x-2)2+,
∴顶点坐标为(2,),
∴顶点在 x 轴上方,不符合题意.
20.解:任务1:以顶棚最高点为坐标原点,过原点的水平线为轴建立平面直角坐标系.
由题意可知,顶点是,
设,
把点代入得:
解得:,
.
任务2:以顶棚最高点为坐标原点,过原点的水平线为轴建立平面直角坐标系,如图:
∵OA=1.45m,OO'=4m,CE=DF=1m,EF=20m,
∴点A坐标(0,-2.55),D点坐标(10,-3)
抛物线的形状与相同,
∴设
把代入得:,
解得:
处喷出的水流在距离点水平距离4.55米时达到最高.
任务3:调整喷水口的高度时,抛物线的形状不变,且,即原本经过点D(10,-3),平移后经过点F(10,-4)
抛物线往下移动1米时,水流喷灌时恰好落在边缘处.
21.(1)
(2)
(3)
22.(1)
(2)
(3)A或B; b; b; b或 b; b或 b
解:(1)∵点H是AD的中点,
∴AH= AD,
∵正方形AEOH∽正方形ABCD,
∴相似比为: = ;
故答案为: ;
( 2 )在Rt△ABC中,AC=4,BC=3,根据勾股定理得,AB=5,
∴△ACD与△ABC相似的相似比为: ,
故答案为: ;
( 3 )A、①∵矩形ABEF∽矩形ABCD,
∴AF:AB=AB:AD,
即 a:b=b:a,
∴a= b;
故答案为:
②每个小矩形都是全等的,则其边长为b和 a,
则b: a=a:b,
∴a= b;
故答案为:
B、①如图2,
由①②可知纵向2块矩形全等,横向3块矩形也全等,
∴DN= b,
Ⅰ、当FM是矩形DFMN的长时,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD: b=a:b,
解得FD= a,
∴AF=a﹣ a= a,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 a:b=b:a
得:a= b;
Ⅱ、当DF是矩形DFMN的长时,
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD: b=b:a
解得FD= ,
∴AF=a﹣ ,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 :b=b:a,
得:a= b;
故答案为: 或 ;
②如图3,
由①②可知纵向m块矩形全等,横向n块矩形也全等,
∴DN= b,
Ⅰ、当FM是矩形DFMN的长时,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD: b=a:b,
解得FD= a,
∴AF=a﹣ a,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 a:b=b:a
得:a= b;
Ⅱ、当DF是矩形DFMN的长时,
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD: b=b:a
解得FD= ,
∴AF=a﹣ ,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 :b=b:a,
得:a= .
故答案为: b或 .
1 / 1
一、单选题
1.将抛物线向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A. B.
C. D.
2.下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图象”是随机事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“概率为0.0001的事件”是不可能事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
3.如图,在△ABC中,DE∥BC,若AD:DB=1:3,DE=4,则BC=( )
A.10 B.12 C.15 D.16
4.抛物线y=﹣x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
A.x<1 B.﹣3<x<1 C.x>1 D.x>﹣3
5.如图,已知AB=AC,∠B<30°,BC上一点D满足∠BAD=120°,=,则的值为( )
A. B. C. D.
6.如图,PA,PB分别与⊙O相切于A,B两点,∠P=72°,点D是劣弧上的一点,则∠ADB=( )
A.108° B.72° C.54° D.126°
7.我们知道订书针的两条短边垂直长边.如图是由三枚完全相同的订书针,,拼成的图形,点B,E,C,F在同一条直线上,点D,K,L分别在,,上,,.当点,I重合时,的长度为( )
A. B. C. D.
8.如图,抛物线的对称轴为直线,若关于x的一元二次方程(t为实数)在的范围内有解,则t的取值范围是( )
A. B. C. D.
9.如图,在中,,是的内切圆,连接,交于点D、E,已知,则图中阴影部分的面积是( )
A. B. C. D.
10.如图,正方形中,点M,N分别为,上的动点,且,,交于点 E,点 F 为 的中点,点P为上一个动点,连接,.若,则 的最小值为( )
A. B. C.5 D.
二、填空题
11.如果函数是二次函数,那么的值是 .
12.现将背面完全相同,正面分别标有数﹣2,﹣1,0,1,2的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的相反数作为点P的纵坐标,则点P落在直线 上方的概率为 .
13.如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为 .
14.已知二次函数(m为常数)的图象与x轴有交点,且当x<-3时,y随x的增大而增大,则m的取值范围是
15.如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8 ,△D′PH的面积是4 ,则矩形ABCD的面积等于 .
16.婆罗摩笈多是公元7世纪的古印度伟大数学家,曾研究对角线互相垂直的圆内接四边形,我们把这类四边形称为“婆罗摩笈多四边形”.如图,四边形是的内接四边形,且是“婆罗摩笈多四边形”、若,则的半径为 .
三、解答题
17.如图所示,在⊙O中直径AB垂直于弦CD,垂足为E,若BE=2 ,CD=6 .求⊙O的半径.
18.某班在爱心义卖活动中设立了一个可以自由转动的转盘,如下图所示,同时规定:顾客购物满20元就能获得一次转动转盘的机会,下表是活动中的统计数据:
转动转盘的次数n 100 200 300 400 500
落在“谢谢参与”区域的次数m 29 60 93 122 b
落在“谢谢参与”区域的频率 0.29 0.3 0.31 a 0.296
(1)完成上述表格:______,______;
(2)若继续不停转动转盘,当n很大时,落在“谢谢参与”区域的频率将会接近______,假如你去转动该转盘一次,你转到“谢谢参与”的概率约是______;(结果都精确到0.1)
(3)顾客转动转盘一次,得到奖品“盲盒”的概率记为,得到奖品“贴纸”的概率记为,得到“谢谢参与”的概率记为,则、、的大小关系是______.(用“>”连接)
19.已知函数 y = kx2 + (k +1)x +1(k 为实数),
(1)当 k=3 时,求此函数图象与 x 轴的交点坐标;
(2)判断此函数与 x 轴的交点个数,并说明理由;
(3)当此函数图象为抛物线,且顶点在 x 轴下方,顶点到 y 轴的距离为 2,求 k 的值.
20.根据以下素材,探索完成任务.
素材1 某学校一块劳动实践基地大棚的横截面如图所示,上部分的顶棚是抛物线形状,下部分是由两根立柱和组成,立柱高为,顶棚最高点距离地面是,的长为.
素材2 为提高灌溉效率,学校在的中点处安装了一款可垂直升降的自动喷灌器,从喷水口喷出的水流可以看成抛物线,其形状与的图象相同,,此时水流刚好喷到立柱的端点处.
问题解决
任务1 确定顶棚的形状 以顶棚最高点为坐标原点建立平面直角坐标系,求出顶棚部分抛物线的表达式.
任务2 探索喷水的高度 问处喷出的水流在距离点水平距离为多少米时达到最高.
任务3 调整喷头的高度 如何调整喷水口的高度(形状不变),使水流喷灌时恰好落在边缘处.
21.如图1,四边形内接于,为直径,,,交于点E,,过点O作,垂足为G,交于点H.
(1)求的半径;
(2)当时,求的值;
(3)延长交的延长线于点Q,当时,求的长.
22.阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).
答案解析部分
1.A
2.D
3.D
4.B
5.A
解:如图,作BE∥AC交AD于E,作BH⊥AE于H,
∵AB=AC,
∴∠ABC=∠C,
∵BE∥AC,
∴∠DBE=∠C,
∴∠ABC=∠DBE,
∵∠DBE=∠C,∠ADC=∠EDB,
∴△ADC∽△EDB,
∴,
设AB=AC=6a,
∴BE=14a,
∵∠BAD=120°,BH⊥AE,
∴∠ABH=30°,
∴,,
∴,
在Rt△BEH中,根据勾股定理,得
∵EH2=BE2-BH2,
∴
∴,
即,
解得AD=3a,
则;
6.D
解:∵PA,PB分别与⊙O相切于A,B两点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°-72°=108°,
∴,
∵四边形ADBC是圆内接四边形,
∴∠ACB+∠ADB=180°,
∴∠ADB=180°-∠ACB=180°-54°=126°,
7.B
8.B
9.B
10.B
11.0
12.
13.5
14.
解:二次函数(m为常数)的图象与x轴有交点 ,则令得则解得,又因为当x<-3时,y随x的增大而增大 ,且,函数开口向下,则对称轴直线方程:,综上所述
15.8(3 +2 )
【解答】解:由翻折可知:
∠A=∠A′=90°,∠D=∠D′=90°,
∵∠FPG=90°,
∴∠A′=∠FPG,
∴A′E∥PF,
∴∠A′EP=∠D′PH,
∴△AE′P∽△D′PH,
∴ ,
∵AB=CD,AB=A′P,CD=D′P,
∴A′P=D′P,
∵ ,
∴A′E= D′P,
∴S△A′EP= A′E A′P= × D′P D′P=8 ,
解得D′P=4(负值舍去),
∴A′P=D′P=4,
∴AE=A′E=4 ,
∴EP= ,
∴PH=
DH=D′H= 2 ,
∴AD=AE+EP+PH+DH
=4 +4 +2 +2
=6 +4 +2 .
AB=A′P=4,
∴S矩形ABCD=AB AD
=4(6 +4 +2 )
=8(3 +2 + ).
16.1
17.解: 连接OD,设半径为r,
∵AB⊥CD, ∵CD=6,
∴CE=DE=3,
∵BE=2,∴OE=r-2
∴在Rt△OED中,r =3 +(r-2) ,
解得:r=
18.(1))0.305,148
(2)0.3,0.3
(3)
19.(1)解: ∵k=3 ,∴ y=3x2+4x+1,
令 y=0,∴ 3x2+4x+1=0, 解得:x1=-1,x2=- ,
∴此函数图象与 x 轴的交点坐标为(-1,0),(- ,0).
(2)解:∵y = kx2 + (k +1)x +1,
∴①当 k=0 时,
函数为 y=x+1,
此函数图象与 x 轴有一个公共点;
②当 k≠0 时,
∴△=b2-4ac=(k+1)2-4k=(k-1)2,
若 k=1 则△=0,它的图象与 x 轴有一个公共点;
若 k≠1 则 △>0,它的图象与 x 轴有两个公共点;
∴当 k=0 或 1 时, 它的图象与 x 轴有一个公共点; 当 k≠0 且 k≠1 时,图象与与 x 轴有两个公共点.
(3)解:依题可得:
=2,
解得:k=或k=-,
①当k=时,
∴y=(x+2)2-,
∴顶点坐标为(-2,-),
∴顶点在 x 轴下方,满足题意;
②当k=- 时,
∴y=-(x-2)2+,
∴顶点坐标为(2,),
∴顶点在 x 轴上方,不符合题意.
20.解:任务1:以顶棚最高点为坐标原点,过原点的水平线为轴建立平面直角坐标系.
由题意可知,顶点是,
设,
把点代入得:
解得:,
.
任务2:以顶棚最高点为坐标原点,过原点的水平线为轴建立平面直角坐标系,如图:
∵OA=1.45m,OO'=4m,CE=DF=1m,EF=20m,
∴点A坐标(0,-2.55),D点坐标(10,-3)
抛物线的形状与相同,
∴设
把代入得:,
解得:
处喷出的水流在距离点水平距离4.55米时达到最高.
任务3:调整喷水口的高度时,抛物线的形状不变,且,即原本经过点D(10,-3),平移后经过点F(10,-4)
抛物线往下移动1米时,水流喷灌时恰好落在边缘处.
21.(1)
(2)
(3)
22.(1)
(2)
(3)A或B; b; b; b或 b; b或 b
解:(1)∵点H是AD的中点,
∴AH= AD,
∵正方形AEOH∽正方形ABCD,
∴相似比为: = ;
故答案为: ;
( 2 )在Rt△ABC中,AC=4,BC=3,根据勾股定理得,AB=5,
∴△ACD与△ABC相似的相似比为: ,
故答案为: ;
( 3 )A、①∵矩形ABEF∽矩形ABCD,
∴AF:AB=AB:AD,
即 a:b=b:a,
∴a= b;
故答案为:
②每个小矩形都是全等的,则其边长为b和 a,
则b: a=a:b,
∴a= b;
故答案为:
B、①如图2,
由①②可知纵向2块矩形全等,横向3块矩形也全等,
∴DN= b,
Ⅰ、当FM是矩形DFMN的长时,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD: b=a:b,
解得FD= a,
∴AF=a﹣ a= a,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 a:b=b:a
得:a= b;
Ⅱ、当DF是矩形DFMN的长时,
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD: b=b:a
解得FD= ,
∴AF=a﹣ ,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 :b=b:a,
得:a= b;
故答案为: 或 ;
②如图3,
由①②可知纵向m块矩形全等,横向n块矩形也全等,
∴DN= b,
Ⅰ、当FM是矩形DFMN的长时,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD: b=a:b,
解得FD= a,
∴AF=a﹣ a,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 a:b=b:a
得:a= b;
Ⅱ、当DF是矩形DFMN的长时,
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD: b=b:a
解得FD= ,
∴AF=a﹣ ,
∴AG= ,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 :b=b:a,
得:a= .
故答案为: b或 .
1 / 1
同课章节目录
