8.1 分数的初步认识 知识梳理 (课件)(共23张PPT)人教版数学三年级上册
文档属性
| 名称 | 8.1 分数的初步认识 知识梳理 (课件)(共23张PPT)人教版数学三年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 437.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
8.1 分数的初步认识 知识梳理
第 1 课时 几分之一
■考点一 认识几分之一
第 1 课时 几分之一
1. 把一个物体或图形平均分成若干份,其中的 1 份就用几分之一表示。
2. 在分数中,分数中间的横线叫作
分数线,分数线上面的数字叫作分子,
分数线下面的数字叫作分母。(如右图)
3. 读法:先读分母,再读分数线,最后读分子。
如: 读作:二分之一。
4. 写法:先写分数线,再写分母,最后写分子。
第 1 课时 几分之一
易错警示
把一个物体或图形平均分成几份,不管分成的是什么形状,每一份都是这个物体或图形的几分之一。
第 1 课时 几分之一
重难突破
只有平均分才能产生分数吗?
答:是的。 例如“把一块月饼分成 2 份,每份是这块月饼的 ”的说法是错误的,因为没有明确是否把这块月饼平均分成 2 份,如果不是平均分,就不能用 表示。
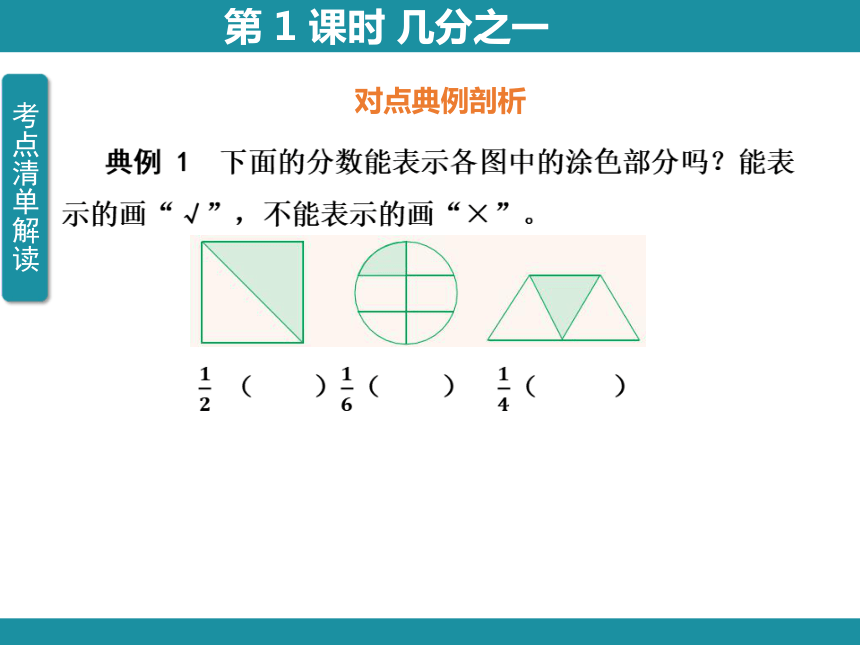
典例 1 下面的分数能表示各图中的涂色部分吗?能表示的画“√”,不能表示的画“×”。
( )( ) ( )
第 1 课时 几分之一
对点典例剖析
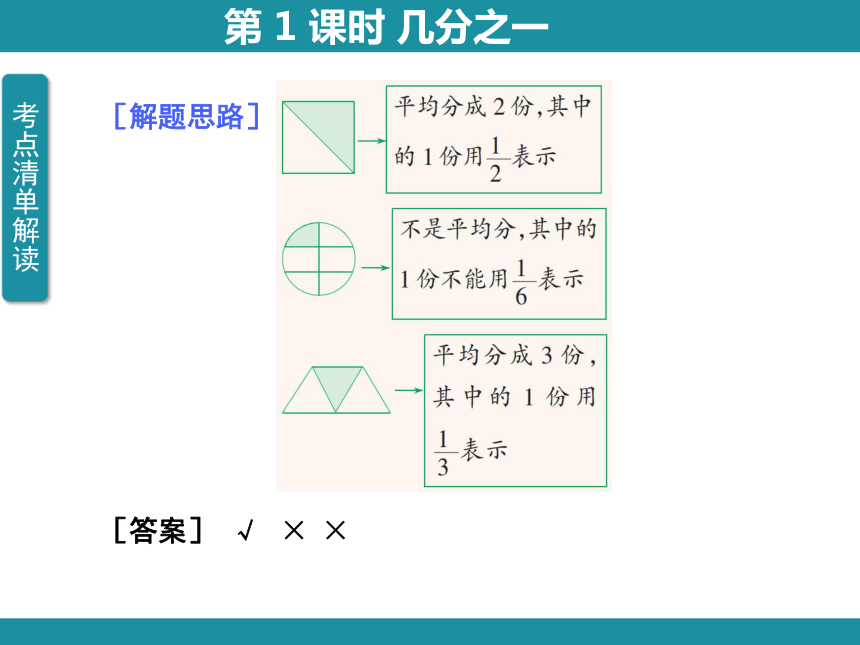
[解题思路]
[答案] √ × ×
第 1 课时 几分之一
■考点二 比较几分之一的大小
第 1 课时 几分之一
分子是 1 的两个分数比较大小,分母越大,分数越小;分母越小,分数越大。如: > 。
第 1 课时 几分之一
重难突破
为什么分子是 1 的分数,分母越大,分数越小,分母越小,分数越大?
答:在分数里,分母表示把一个物体平均分成的份数,当平均分成的份数越多时,每份越少;当平均分成的份数越少时,每份越多。
典例 2 比一比。
第 1 课时 几分之一
对点典例剖析
[解题思路] 根据分数的意义比较。把一个物体或图形平均分成的份数越少,每一份越大。
[答案]>
第 1 课时 几分之一
■方法:用转化法巧写分数
第 1 课时 几分之一
转化法是指将未解决的问题,通过某种途径转化为已解决的或易解的问题,最终使原问题获得解决的一种方法。
第 1 课时 几分之一
例 涂色部分占整个图形的几分之几?
( )
第 1 课时 几分之一
[解析] 涂色部分不在一起,可以通过移动将涂色部分转化到一起,如下图。
[答案]
第 2 课时 几分之几
■考点一 认识几分之几
1. 把一个物体或图形平均分成几份,其中的几份就用几分之几表示。分母表示分成的总份数,分数线表示平均分,分子表示所取的份数。
2. 几分之几可以看成几个几分之一。
第 2 课时 几分之几
重难突破
一个分数的分子和分母相同时,表示什么?
答:表示把一个物体或图形平均分成几份,全部取出,也就是整个图形,所以可以用 1 表示。
典例 1 用分数表示图中的涂色部分。
第 2 课时 几分之几
对点典例剖析
[解题思路] 图形平均分成 6 份,每份占这个圆的 ,2 份就是 2 个 ,就是 。
[答案]
第 2 课时 几分之几
■考点二 同分母分数的大小比较
第 2 课时 几分之几
同分母分数比较大小的方法:分子越大,分数越大;分子越小,分数越小。
第 2 课时 几分之几
重难突破
如何理解同分母分数比较大小,分子越大,分数越大?
答:把一个整体平均分成几份,取的份数越多,所得的分数就越大。
典例 2 比较大小。
第 2 课时 几分之几
对点典例剖析
[解题思路]
[答案] >
第 2 课时 几分之几
8.1 分数的初步认识 知识梳理
第 1 课时 几分之一
■考点一 认识几分之一
第 1 课时 几分之一
1. 把一个物体或图形平均分成若干份,其中的 1 份就用几分之一表示。
2. 在分数中,分数中间的横线叫作
分数线,分数线上面的数字叫作分子,
分数线下面的数字叫作分母。(如右图)
3. 读法:先读分母,再读分数线,最后读分子。
如: 读作:二分之一。
4. 写法:先写分数线,再写分母,最后写分子。
第 1 课时 几分之一
易错警示
把一个物体或图形平均分成几份,不管分成的是什么形状,每一份都是这个物体或图形的几分之一。
第 1 课时 几分之一
重难突破
只有平均分才能产生分数吗?
答:是的。 例如“把一块月饼分成 2 份,每份是这块月饼的 ”的说法是错误的,因为没有明确是否把这块月饼平均分成 2 份,如果不是平均分,就不能用 表示。
典例 1 下面的分数能表示各图中的涂色部分吗?能表示的画“√”,不能表示的画“×”。
( )( ) ( )
第 1 课时 几分之一
对点典例剖析
[解题思路]
[答案] √ × ×
第 1 课时 几分之一
■考点二 比较几分之一的大小
第 1 课时 几分之一
分子是 1 的两个分数比较大小,分母越大,分数越小;分母越小,分数越大。如: > 。
第 1 课时 几分之一
重难突破
为什么分子是 1 的分数,分母越大,分数越小,分母越小,分数越大?
答:在分数里,分母表示把一个物体平均分成的份数,当平均分成的份数越多时,每份越少;当平均分成的份数越少时,每份越多。
典例 2 比一比。
第 1 课时 几分之一
对点典例剖析
[解题思路] 根据分数的意义比较。把一个物体或图形平均分成的份数越少,每一份越大。
[答案]>
第 1 课时 几分之一
■方法:用转化法巧写分数
第 1 课时 几分之一
转化法是指将未解决的问题,通过某种途径转化为已解决的或易解的问题,最终使原问题获得解决的一种方法。
第 1 课时 几分之一
例 涂色部分占整个图形的几分之几?
( )
第 1 课时 几分之一
[解析] 涂色部分不在一起,可以通过移动将涂色部分转化到一起,如下图。
[答案]
第 2 课时 几分之几
■考点一 认识几分之几
1. 把一个物体或图形平均分成几份,其中的几份就用几分之几表示。分母表示分成的总份数,分数线表示平均分,分子表示所取的份数。
2. 几分之几可以看成几个几分之一。
第 2 课时 几分之几
重难突破
一个分数的分子和分母相同时,表示什么?
答:表示把一个物体或图形平均分成几份,全部取出,也就是整个图形,所以可以用 1 表示。
典例 1 用分数表示图中的涂色部分。
第 2 课时 几分之几
对点典例剖析
[解题思路] 图形平均分成 6 份,每份占这个圆的 ,2 份就是 2 个 ,就是 。
[答案]
第 2 课时 几分之几
■考点二 同分母分数的大小比较
第 2 课时 几分之几
同分母分数比较大小的方法:分子越大,分数越大;分子越小,分数越小。
第 2 课时 几分之几
重难突破
如何理解同分母分数比较大小,分子越大,分数越大?
答:把一个整体平均分成几份,取的份数越多,所得的分数就越大。
典例 2 比较大小。
第 2 课时 几分之几
对点典例剖析
[解题思路]
[答案] >
第 2 课时 几分之几
