沪科版初中数学八年级上册第15章15.4 角平分线的性质(共22张PPT)
文档属性
| 名称 | 沪科版初中数学八年级上册第15章15.4 角平分线的性质(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 337.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-31 11:13:20 | ||
图片预览




文档简介
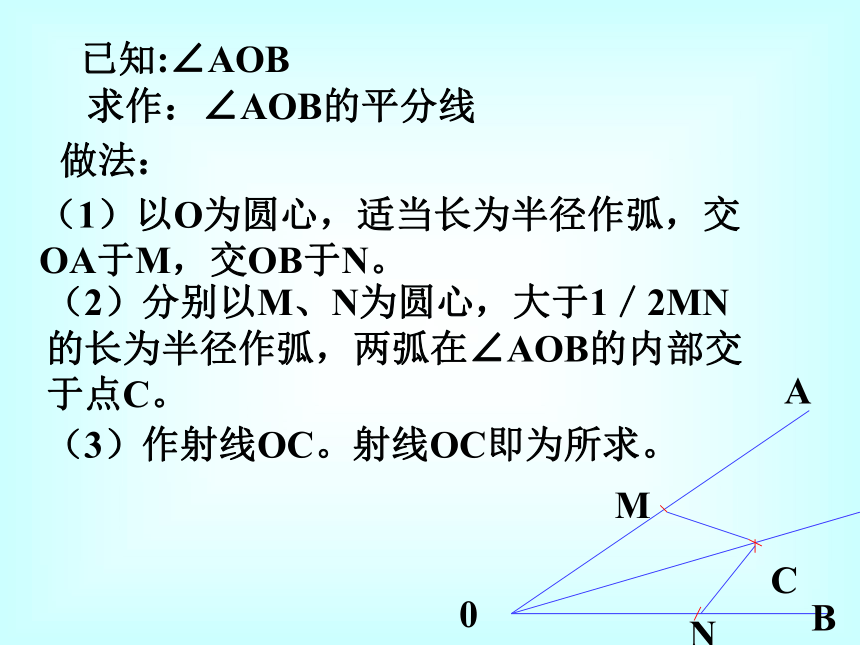
课件22张PPT。角平分线的性质已知:∠AOB求作:∠AOB的平分线(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。(2)分别以M、N为圆心,大于1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。(3)作射线OC。射线OC即为所求。
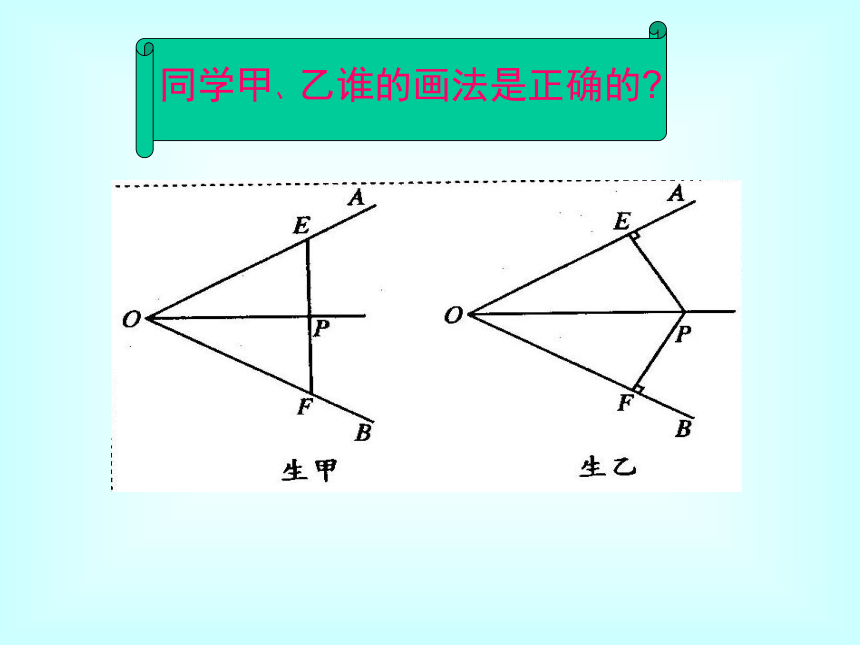
A0BMNC做法: 将AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论? 可以看一看,第一条折痕是AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到AOB两边的距离,这两个距离相等.折一折探究2: 按照做一做的顺序画∠AOB的折痕OC ,过点P的垂线段PD、PE ,并度量所画PD、PE是否等长?画一画同学甲、乙谁的画法是正确的?议一议:由折一折和画一画你可得到什么猜想?能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话.请填下表:PD=PEOC平分∠AOB,PD⊥OA, PE⊥OB, D、E为垂足.
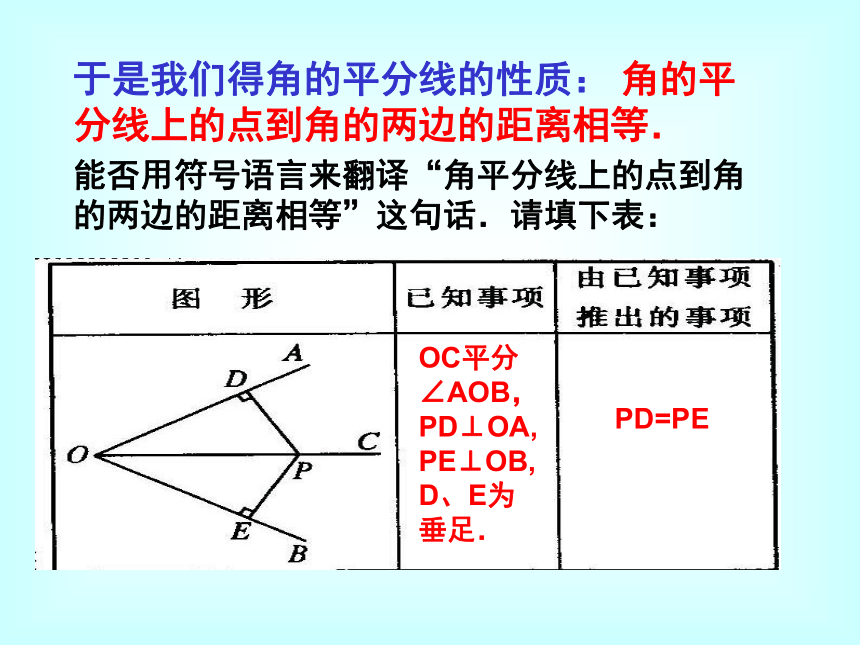
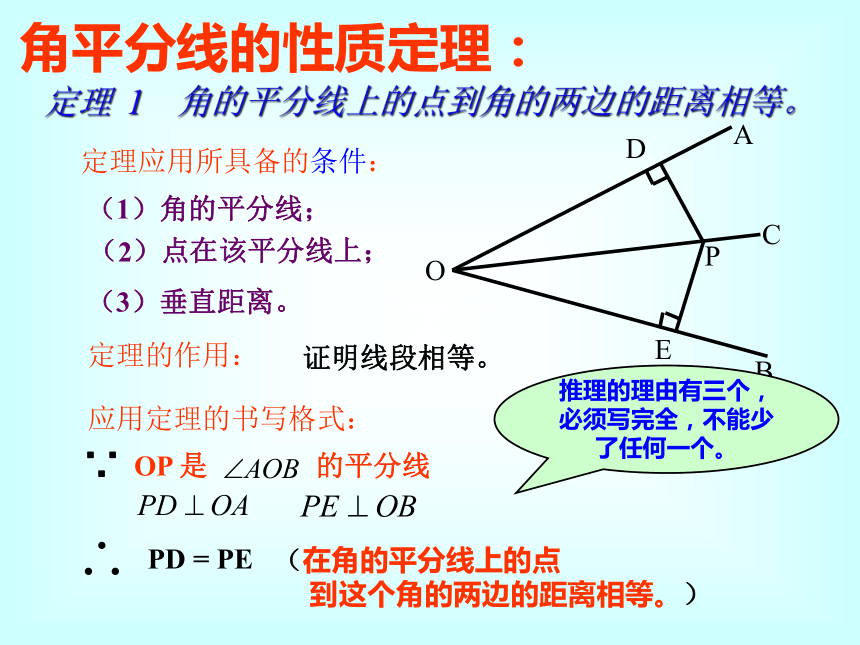
于是我们得角的平分线的性质: 角的平分线上的点到角的两边的距离相等.角平分线的性质定理: 定理 1 角的平分线上的点到角的两边的距离相等。定理应用所具备的条件:定理的作用: 证明线段相等。应用定理的书写格式:OP 是 的平分线PD = PE(在角的平分线上的点
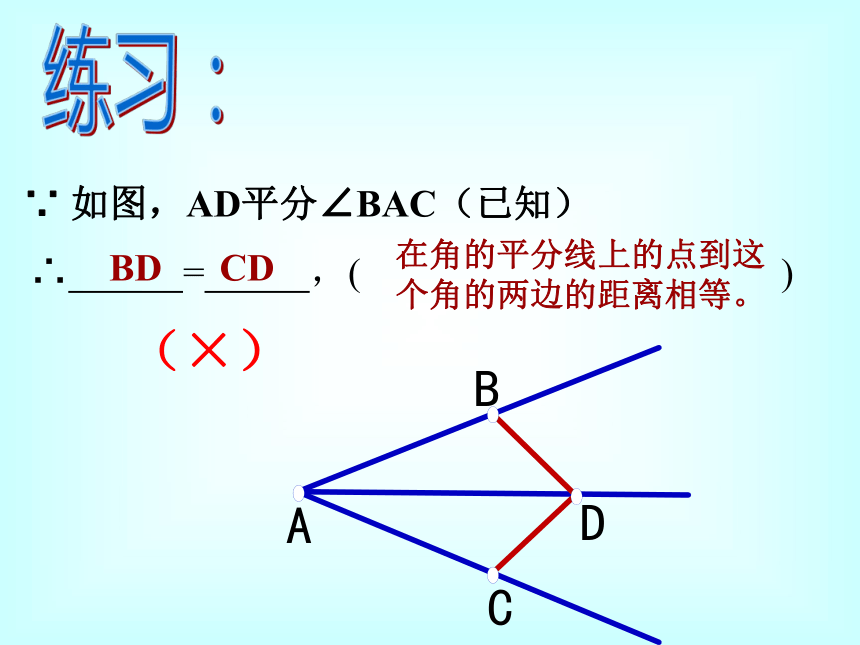
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)练习:∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×) 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.思考证明: ∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义) 在Rt△QDO和Rt△QEO中
QO=QO(公共边) QD=QE ∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠ QOD=∠QOE
∴点Q在∠AOB的平分线上已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.这样,我们又可以得到一个结论: 到角的两边距离相等的点在角的平分线上。证明:过点P作PD 、PE、PF分别垂直于AB、
BC、CA,垂足分别为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边
的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等想一想,点P在∠A 的 平分线上吗?这说明三角形的三条角平分线有什么关系?,B如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD?为什么?PD,PE没有垂直OA,OB,它们不是角平分线上任一点这个角两边的距离,所以不一定相等.思考:要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于MGHM∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC∴FG=FM又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC∴FM=FH∴FG=FH∴点F在∠DAE的平分线上 利用结论,解决问题练一练 1、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
拓展与延伸2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处分析:由于没有限制在何处选址,故要求的地址共有四处。练习2: 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
A0BMNC做法: 将AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论? 可以看一看,第一条折痕是AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到AOB两边的距离,这两个距离相等.折一折探究2: 按照做一做的顺序画∠AOB的折痕OC ,过点P的垂线段PD、PE ,并度量所画PD、PE是否等长?画一画同学甲、乙谁的画法是正确的?议一议:由折一折和画一画你可得到什么猜想?能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话.请填下表:PD=PEOC平分∠AOB,PD⊥OA, PE⊥OB, D、E为垂足.
于是我们得角的平分线的性质: 角的平分线上的点到角的两边的距离相等.角平分线的性质定理: 定理 1 角的平分线上的点到角的两边的距离相等。定理应用所具备的条件:定理的作用: 证明线段相等。应用定理的书写格式:OP 是 的平分线PD = PE(在角的平分线上的点
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。∵ 如图,AD平分∠BAC(已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×)练习:∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
√不必再证全等∵ 如图, DC⊥AC,DB⊥AB (已知) ∴ = ,( ) 在角的平分线上的点到这个角的两边的距离相等。
BD CD(×) 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.思考证明: ∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义) 在Rt△QDO和Rt△QEO中
QO=QO(公共边) QD=QE ∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠ QOD=∠QOE
∴点Q在∠AOB的平分线上已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.这样,我们又可以得到一个结论: 到角的两边距离相等的点在角的平分线上。证明:过点P作PD 、PE、PF分别垂直于AB、
BC、CA,垂足分别为D、E、F
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE(在角平分线上的点到角的两边
的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、
CA的距离相等想一想,点P在∠A 的 平分线上吗?这说明三角形的三条角平分线有什么关系?,B如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD?为什么?PD,PE没有垂直OA,OB,它们不是角平分线上任一点这个角两边的距离,所以不一定相等.思考:要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000)如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于MGHM∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC∴FG=FM又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC∴FM=FH∴FG=FH∴点F在∠DAE的平分线上 利用结论,解决问题练一练 1、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
拓展与延伸2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处分析:由于没有限制在何处选址,故要求的地址共有四处。练习2: 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
