八年级上册11.2与三角形有关的角同步训练(含解析)
文档属性
| 名称 | 八年级上册11.2与三角形有关的角同步训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 550.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 00:00:00 | ||
图片预览


文档简介
八年级上册11.2 与三角形有关的角 同步训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,是延长线上一点,过点作于点,若,则( )
A. B. C. D.
2.一个三角形中直角的个数最多有( )
A.3 B.1 C.2 D.0
3.如图,△ABC的角平分线BO、CO相交于点O,∠A=120°,则∠BOC=( )
A.150° B.140° C.130° D.120°
4.在中,的对边分别记为a,b,c,则由下列条件能判定为直角三角形的有( )
(1)
(2)
(3)
(4)
A.1个 B.2个 C.3个 D.4个
二、填空题
5.如图,,,,则 .
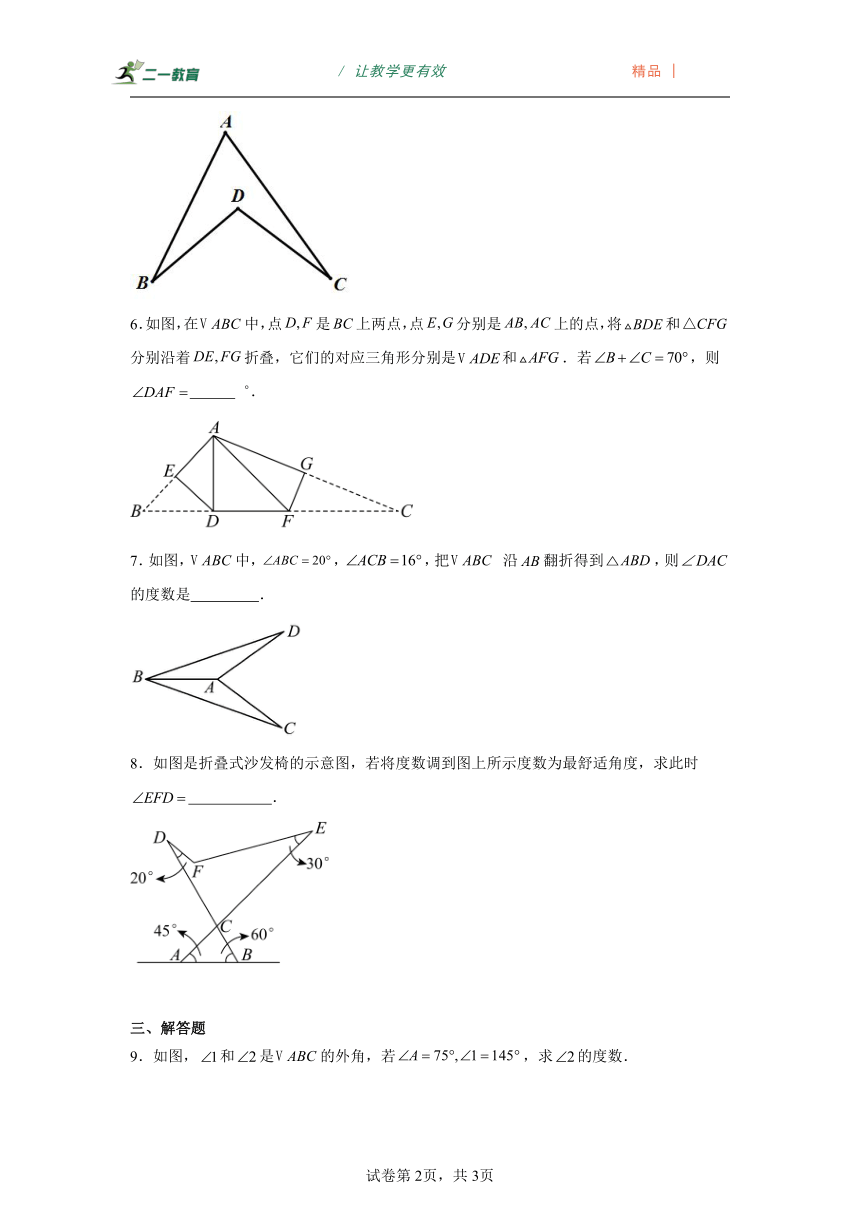
6.如图,在中,点是上两点,点分别是上的点,将和分别沿着折叠,它们的对应三角形分别是和.若,则 .
7.如图,中,,,把 沿翻折得到,则的度数是 .
8.如图是折叠式沙发椅的示意图,若将度数调到图上所示度数为最舒适角度,求此时 .
三、解答题
9.如图,和是的外角,若,求的度数.
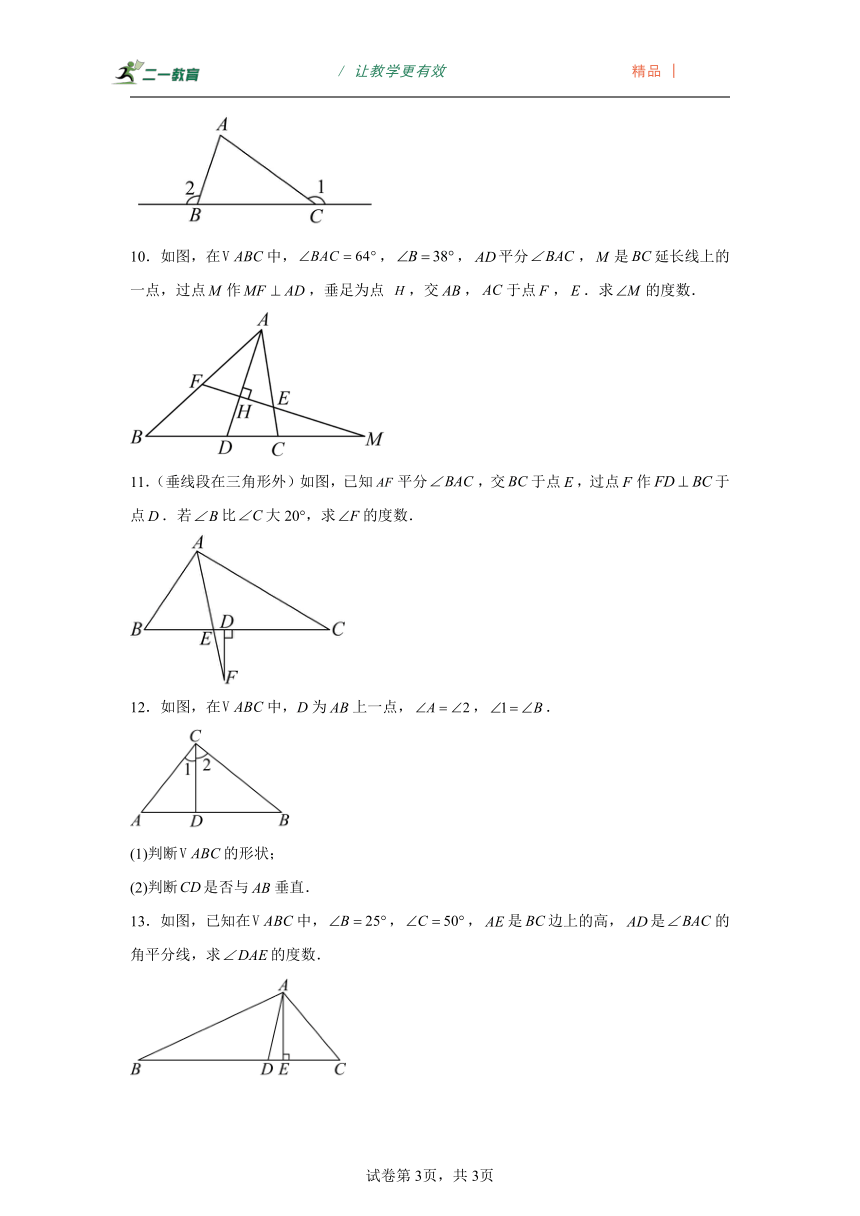
10.如图,在中,,,平分,是延长线上的一点,过点作,垂足为点 ,交,于点,.求的度数.
11.(垂线段在三角形外)如图,已知平分,交于点,过点作于点.若比大20°,求的度数.
12.如图,在中,D为上一点,,.
(1)判断的形状;
(2)判断是否与垂直.
13.如图,已知在中,,,是边上的高,是的角平分线,求的度数.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题考查了三角形的内角和定理,外角性质,掌握三角形的外角性质是解题的关键.
根据三角形的外角性质可得,由此解答即可.
【详解】解:,
,
,,
,
.
,
,
.
故选:A.
2.B
【分析】根据三角形三个内角的和等于180°解答即可.
【详解】根据三角形内角和是180°可知,一个三角形中直角的个数最多有1个.
故选B.
【点睛】本题考查了三角形内角和定理,熟练掌握三角形三个内角的和等于180°是解答本题的关键.
3.A
【详解】解:∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB=30°,
∴∠BOC=150°.
故选A.
4.C
【分析】本题考查了三角形内角和定理、勾股定理逆定理,根据三角形内角和定理和勾股定理逐项判断即可得出答案.
【详解】解:(1)∵,,
∴,
∴,
∴为直角三角形;
(2)∵,,
∴,
∴为直角三角形;
(3)∵,
∴,
∴为直角三角形;
(4)∵,
∴设,,(其中),
∴,
∴不是直角三角形,
故选:C.
5.
【分析】如图所示,连接,在中,可求出的度数,由此可求出的度数,在中,根据三角形的内角和定理即可求解.
【详解】解:如图所示,连接,
在中,,
∴,
∵,,
∴,
在中,,
∴,
故答案为:.
【点睛】本题主要考查三角新的内角和定理的运用,掌握三角形内角和为及角的和差计算是解题的关键.
6.40
【分析】本题考查了折叠的性质以及三角形内角和定理.由折叠的性质得,,利用三角形内角和定理即可求解.
【详解】解:由折叠的性质得,,
又∵,
∴
,
故答案为:40.
7./72度
【分析】延长到,由折叠的性质可得:,,根据三角形的外角可得:,,即可求解,
本题考查了,折叠的性质,三角形的外角,解题的关键是:添加辅助线,根据用三角形的外角表示出所求角.
【详解】解:延长到,
由折叠可得:,,
∵,,
∴,
故答案为:.
8.
【分析】本题主要考查三角形内角和定理和三角形外角的性质,延长交于点,根据三角形内角和定理求出,得出,再由三角形外角性质可得 .
【详解】解:延长交于点,如图,
∵
∴
∵
∴
∴
∴
故答案为:.
9.
【分析】先根据三角形外角的性质求出的度数,则由平角的定义可得答案.
【详解】解:
,
.
【点睛】本题主要考查了三角形外角的性质,平角的定义,熟知三角形一个外角的度数等于与其不相邻的两个内角的度数之和是解题的关键.
10.
【分析】本题考查了角平分线的定义,垂直的定义,三角形的外角性质,三角形的内角和定理,由角平分线的定义得,由外角性质可得,然后根据三角形的内角和即可求解,熟练掌握知识点的应用是解题的关键.
【详解】∵平分,
∴,
∴,
∵,
∴,
∴ .
11.
【分析】由题意得,由平分,得.另外,得,由,进而求得,可得,由,得,由即可求解.
【详解】由题意知:.
平分,
.
又,
.
.
又,
.
.
,
.
,
.
【点睛】本题主要考查三角形内角和定理以及三角形外角的性质,熟练掌握三角形内角和定理以及三角形外角的性质是解决本题的关键.
12.(1)是直角三角形
(2)
【分析】本题考查了直角三角形的性质,三角形内角和定理,垂直的定义,熟练掌握三角形内角和定理是解题的关键,(1)证出即可得到结论,(2)求出,可得出.
【详解】(1)解:是直角三角形,理由如下:
∵,,
∴,
∴,
∴,
∴是直角三角形.
(2)解:,理由如下:
∵,,
∴,
∴,
∴.
13.
【分析】本题主要考查了三角形内角和定理,角平分线的定义,直角三角形两锐角互余,熟知相关知识是解题的关键.先根据三角形内角和定理求出,再根据角平分线的定义求出,根据直角三角形两锐角互余求出的度数即可得到答案.
【详解】解:∵,,
∴,
∵是的角平分线,
∴,
∵是边上的高,
∴,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,是延长线上一点,过点作于点,若,则( )
A. B. C. D.
2.一个三角形中直角的个数最多有( )
A.3 B.1 C.2 D.0
3.如图,△ABC的角平分线BO、CO相交于点O,∠A=120°,则∠BOC=( )
A.150° B.140° C.130° D.120°
4.在中,的对边分别记为a,b,c,则由下列条件能判定为直角三角形的有( )
(1)
(2)
(3)
(4)
A.1个 B.2个 C.3个 D.4个
二、填空题
5.如图,,,,则 .
6.如图,在中,点是上两点,点分别是上的点,将和分别沿着折叠,它们的对应三角形分别是和.若,则 .
7.如图,中,,,把 沿翻折得到,则的度数是 .
8.如图是折叠式沙发椅的示意图,若将度数调到图上所示度数为最舒适角度,求此时 .
三、解答题
9.如图,和是的外角,若,求的度数.
10.如图,在中,,,平分,是延长线上的一点,过点作,垂足为点 ,交,于点,.求的度数.
11.(垂线段在三角形外)如图,已知平分,交于点,过点作于点.若比大20°,求的度数.
12.如图,在中,D为上一点,,.
(1)判断的形状;
(2)判断是否与垂直.
13.如图,已知在中,,,是边上的高,是的角平分线,求的度数.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题考查了三角形的内角和定理,外角性质,掌握三角形的外角性质是解题的关键.
根据三角形的外角性质可得,由此解答即可.
【详解】解:,
,
,,
,
.
,
,
.
故选:A.
2.B
【分析】根据三角形三个内角的和等于180°解答即可.
【详解】根据三角形内角和是180°可知,一个三角形中直角的个数最多有1个.
故选B.
【点睛】本题考查了三角形内角和定理,熟练掌握三角形三个内角的和等于180°是解答本题的关键.
3.A
【详解】解:∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB=30°,
∴∠BOC=150°.
故选A.
4.C
【分析】本题考查了三角形内角和定理、勾股定理逆定理,根据三角形内角和定理和勾股定理逐项判断即可得出答案.
【详解】解:(1)∵,,
∴,
∴,
∴为直角三角形;
(2)∵,,
∴,
∴为直角三角形;
(3)∵,
∴,
∴为直角三角形;
(4)∵,
∴设,,(其中),
∴,
∴不是直角三角形,
故选:C.
5.
【分析】如图所示,连接,在中,可求出的度数,由此可求出的度数,在中,根据三角形的内角和定理即可求解.
【详解】解:如图所示,连接,
在中,,
∴,
∵,,
∴,
在中,,
∴,
故答案为:.
【点睛】本题主要考查三角新的内角和定理的运用,掌握三角形内角和为及角的和差计算是解题的关键.
6.40
【分析】本题考查了折叠的性质以及三角形内角和定理.由折叠的性质得,,利用三角形内角和定理即可求解.
【详解】解:由折叠的性质得,,
又∵,
∴
,
故答案为:40.
7./72度
【分析】延长到,由折叠的性质可得:,,根据三角形的外角可得:,,即可求解,
本题考查了,折叠的性质,三角形的外角,解题的关键是:添加辅助线,根据用三角形的外角表示出所求角.
【详解】解:延长到,
由折叠可得:,,
∵,,
∴,
故答案为:.
8.
【分析】本题主要考查三角形内角和定理和三角形外角的性质,延长交于点,根据三角形内角和定理求出,得出,再由三角形外角性质可得 .
【详解】解:延长交于点,如图,
∵
∴
∵
∴
∴
∴
故答案为:.
9.
【分析】先根据三角形外角的性质求出的度数,则由平角的定义可得答案.
【详解】解:
,
.
【点睛】本题主要考查了三角形外角的性质,平角的定义,熟知三角形一个外角的度数等于与其不相邻的两个内角的度数之和是解题的关键.
10.
【分析】本题考查了角平分线的定义,垂直的定义,三角形的外角性质,三角形的内角和定理,由角平分线的定义得,由外角性质可得,然后根据三角形的内角和即可求解,熟练掌握知识点的应用是解题的关键.
【详解】∵平分,
∴,
∴,
∵,
∴,
∴ .
11.
【分析】由题意得,由平分,得.另外,得,由,进而求得,可得,由,得,由即可求解.
【详解】由题意知:.
平分,
.
又,
.
.
又,
.
.
,
.
,
.
【点睛】本题主要考查三角形内角和定理以及三角形外角的性质,熟练掌握三角形内角和定理以及三角形外角的性质是解决本题的关键.
12.(1)是直角三角形
(2)
【分析】本题考查了直角三角形的性质,三角形内角和定理,垂直的定义,熟练掌握三角形内角和定理是解题的关键,(1)证出即可得到结论,(2)求出,可得出.
【详解】(1)解:是直角三角形,理由如下:
∵,,
∴,
∴,
∴,
∴是直角三角形.
(2)解:,理由如下:
∵,,
∴,
∴,
∴.
13.
【分析】本题主要考查了三角形内角和定理,角平分线的定义,直角三角形两锐角互余,熟知相关知识是解题的关键.先根据三角形内角和定理求出,再根据角平分线的定义求出,根据直角三角形两锐角互余求出的度数即可得到答案.
【详解】解:∵,,
∴,
∵是的角平分线,
∴,
∵是边上的高,
∴,
∴,
∴.
答案第1页,共2页
答案第1页,共2页
