八年级数学上册第十一章《三角形》练习卷(含解析)
文档属性
| 名称 | 八年级数学上册第十一章《三角形》练习卷(含解析) | 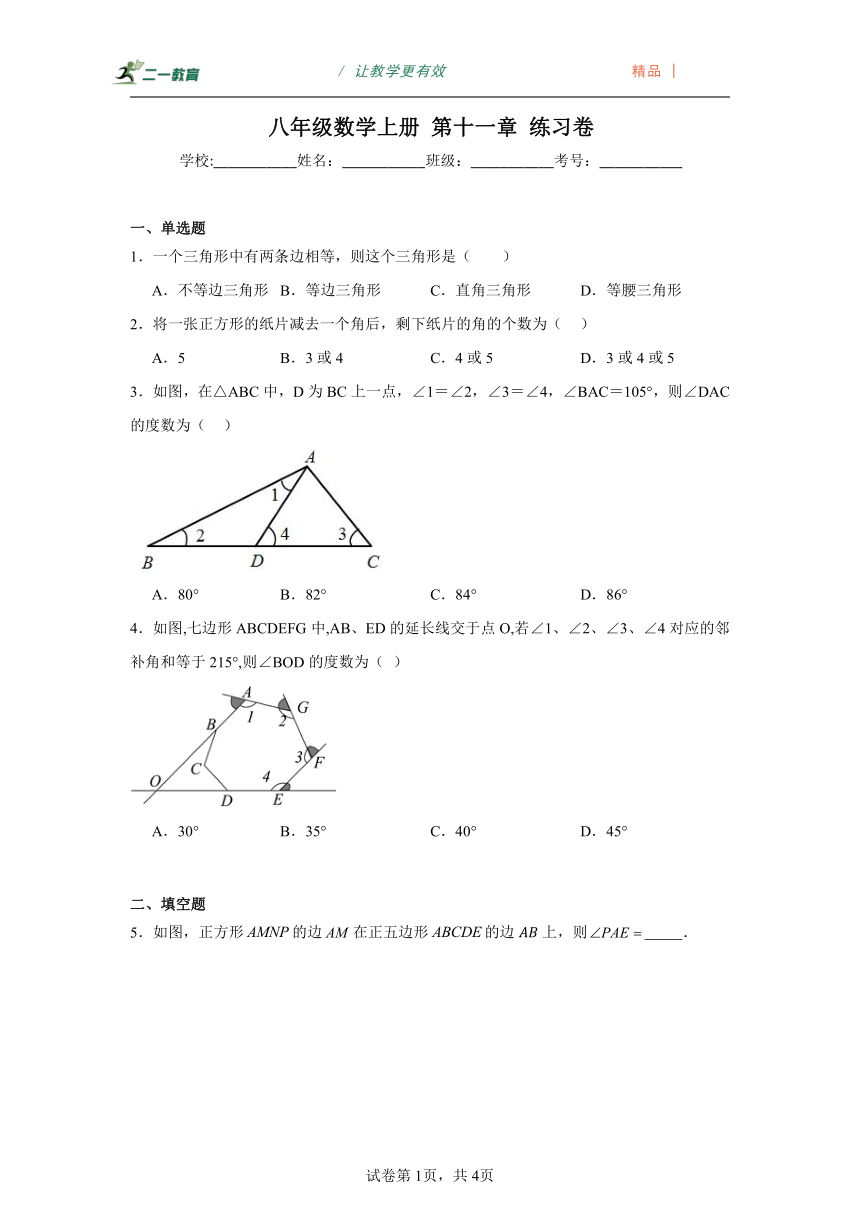 | |
| 格式 | docx | ||
| 文件大小 | 524.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 08:52:19 | ||
图片预览




文档简介
八年级数学上册 第十一章 练习卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个三角形中有两条边相等,则这个三角形是( )
A.不等边三角形 B.等边三角形 C.直角三角形 D.等腰三角形
2.将一张正方形的纸片减去一个角后,剩下纸片的角的个数为( )
A.5 B.3或4 C.4或5 D.3或4或5
3.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为( )
A.80° B.82° C.84° D.86°
4.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1、∠2、∠3、∠4对应的邻补角和等于215°,则∠BOD的度数为( )
A.30° B.35° C.40° D.45°
二、填空题
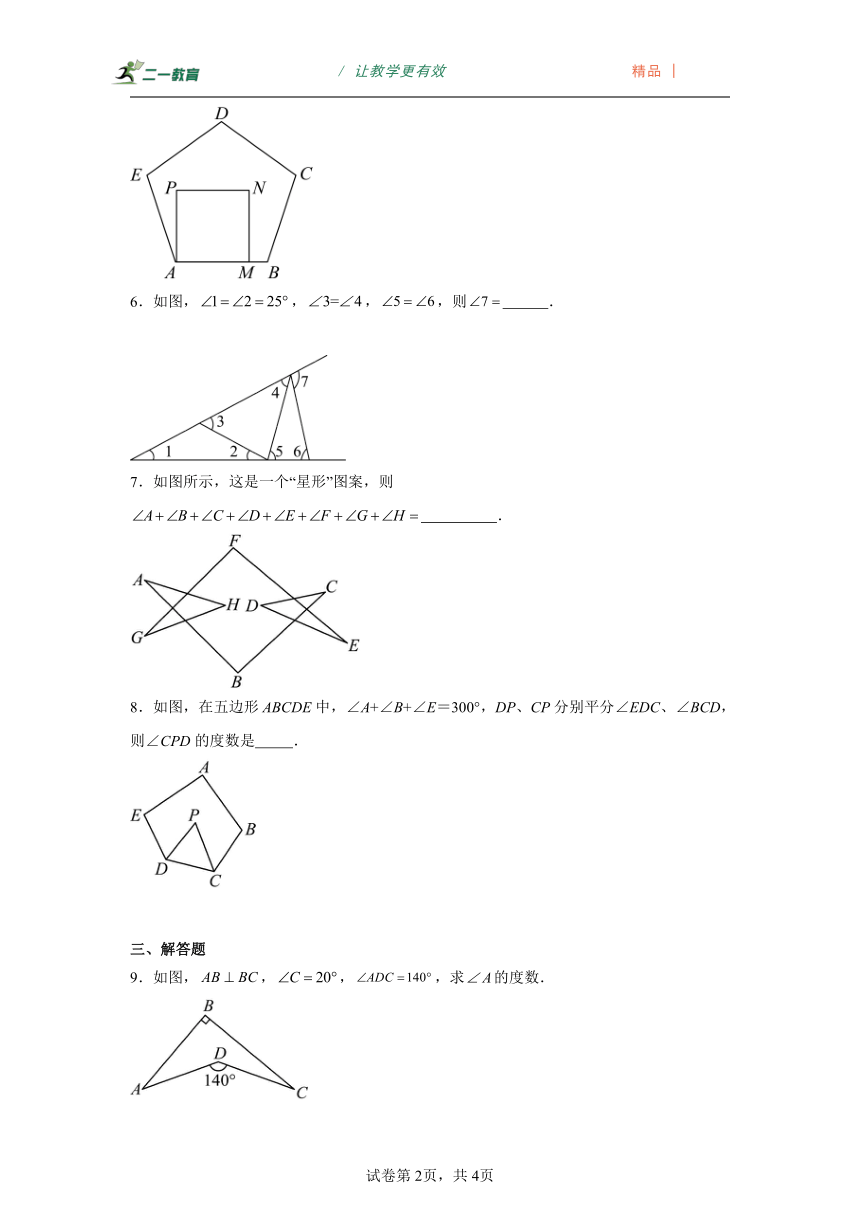
5.如图,正方形的边在正五边形的边上,则 .
6.如图,,,,则 .
7.如图所示,这是一个“星形”图案,则 .
8.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠CPD的度数是 .
三、解答题
9.如图,,,,求的度数.
10.如图所示,有一艘渔船上午九点在A处沿正东方向航行,在A处测得灯塔C在北偏东方向上,行驶到达B处,测得灯塔C在北偏东方向上,求的度数及的度数.
11.如图,若AB∥CD,EF与AB 、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠EFP的度数.
12.(1)如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC,且∠C大于∠B.求证:∠EAD=12(∠C-∠B).
(2)若把问题(1)中的“AD⊥BC于点D”改为“点F为EA上一点且FD⊥BC于点D”,画出新的图形,并说明∠EFD=12(∠C-∠B).
(3)若把问题(2)中的“F为EA上一点”改为“F为AE延长线上的一点”,则问题(2)中的结论成立吗?说明你的理由.
13.中,,点D,E分别是边上的点,点P是一动点.令,,.
(1)若点P在线段上,如图1所示,且,求的度数.
(2)若点P在边上运动,如图2所示,则,,之间有何关系?猜想并说明理由.
(3)若点P运动到边的延长线上,如图3所示,交于点M,,,之间的关系为__________.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查等腰三角形,根据至少有两边相等的三角形叫做等腰三角形,即可判断.
【详解】解:至少有两边相等的三角形叫做等腰三角形.
故选:D.
2.D
【分析】分三种情况,画出图形,即可得出结果.
【详解】解:如图,减去一个角有三种情况,
∴剩下纸片的角的个数为3或4或5;
故选D.
【点睛】本题主要考查了在不同情况下正方形的不同剪法,做此题考虑要全面不要遗漏,解答此题应根据题意,结合图形进行操作,进而得出结论.
3.A
【分析】根据三角形的内角和定理和三角形的外角性质即可解决.
【详解】解:∵∠BAC=105°,
∴∠2+∠3=75°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=75°,
∴∠2=25°.
∴∠DAC=105° 25°=80°.
故选A.
【点睛】此题主要考查了三角形的外角性质以及三角形内角和定理,熟记三角形的内角和定理,三角形的外角性质是解题的关键.
4.B
【分析】在DO延长线上找一点M,根据多边形AOEFG的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【详解】在DO延长线上找一点M,如图所示.
∵多边形AOEFG的外角和为360°,
∴∠BOM=360°-215°=145°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°-∠BOM=180°-145°=35°.
故选B.
【点睛】本题考查了多边形的内角与外角以及邻补角,解题的关键是根据多边形的外角和为360°找出∠BOM=145°.
5./18度
【分析】本题考查的知识点是正多边形的内角问题,解题关键是熟练掌握多边形内角和公式.
先根据多边形内角和公式求出五边形内角和和四边形内角和,再根据正多边形性质求出及,最后由即可求解.
【详解】解:根据多边形内角和计算公式可得:五边形内角和为,
四边形内角和为,
五边形是正五边形,
,
又正方形中,,
.
故答案为:.
6./100度
【分析】本题考查了三角形的外角的性质,熟练掌握三角形的外角性质是解题的关键;
根据三角形的外角性质求出,在根据得出、度数,再次利用三角形外角性质得,即可解答
【详解】,
,
,
,
,
,
故答案为:
7.
【分析】如图,连接,由题意知,,,则,同理可得,,由,可得,即.
【详解】解:如图,连接,
由题意知, ,,
∴,
同理可得,,
∵,
∴,
故答案为:.
【点睛】本题考查了三角形内角和定理,四边形内角和.解题的关键在于明确角度之间的数量关系.
8.60
【分析】根据五边形的内角和求出∠BCD和∠CDE的和,再根据角平分线及三角形内角和求出∠CPD.
【详解】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=540°﹣300°=240°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠PDC+∠PCD=(∠BCD+∠CDE)=120°,
∴∠CPD=180°﹣120°=60°.
故答案是:60.
【点睛】本题解题的关键是知道多边形内角和定理以及角平分线的性质.
9.
【分析】本题考查三角形的外角,延长,交于点,先求出,再根据三角形的外角性质即可得出答案.
【详解】解:如图,延长,交于点.
,
.
,.
.
,,
.
10.45°;
【分析】本题考查的是与方位角的有关计算,三角形的内角和定理与三角形的外角的性质的应用,先由,可得,由,可得,再利用三角形的内角和定理与三角形的外角的性质可得答案.
【详解】解:∵在处测得灯塔在北偏东方向上,
∴,
∴.
∵行驶到达处,测得灯塔在北偏东方向上,
∴,
∴,
∴,
∴.
11.25°
【分析】由EP⊥EF,根据垂直的定义可得∠PEF=90°,根据∠BEF=∠BEP+∠PEF求得∠BEF的度数;又因AB∥CD,根据平行线的性质可得∠BEF+∠EFD=180°,从而求得∠EFD的度数,再由角平分线的定义可得∠EFP的度数,最后根据三角形的内角和定理求得∠EPF的度数.
【详解】解:∵EP⊥EF,∴∠PEF=90°.
∵∠BEP=50°,
∴∠BEF=∠BEP+∠PEF=140°.
∵AB∥CD,∴∠BEF+∠EFD=180°.
∴∠EFD=40°.
∵FP平分∠EFD,∴∠EFP=∠EFD=20°.
∵∠PEF+∠EFP+∠EPF=180°,
∴∠EPF=70°
12.(1)证明见解析; (2)理由见解析;(3)成立,理由见解析.
【详解】(1)在Rt△ADE中,
∵∠AED+∠DAE=90°,∴∠DAE=90°-∠AED.
∵∠AED=180°-∠C-∠CAE,且AE平分∠BAC,∴∠CAE= ∠BAC= (180°-∠C-∠B).∴∠EAD=90°-180°-∠C-1/2(180°-∠C-∠B)= (∠C-∠B).
(2)如图D11-2-5(1),由三角形的内角和定理的推论,得∠FED=∠B+ ∠BAC,故∠B+ ∠BAC+∠EFD=90°①.
在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即∠C+ ∠B+ ∠BAC=90°②.
②-①,得∠EFD= (∠C-∠B).
(3)成立.理由:如图D11-2-5(2),由三角形的内角和定理的推论,得∠FED=∠AEC=∠B+ ∠BAC,
故∠B+ ∠BAC+∠EFD=90°①.
在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即∠C+ ∠B+ ∠BAC=90°②.
②-①,得∠EFD= (∠C-∠B).
13.(1)的度数为;
(2)
(3)
【分析】(1)由题意知,,,由,可得,整理得,,将代入,计算求解即可;
(2)由(1)可知,;
(3)由题意知,,,由,可得,整理即可.
【详解】(1)解:由题意知,,,
∵,
∴,整理得,,
∵,
∴,
∴的度数为;
(2)解:,理由如下:
由(1)可知,;
(3)解:由题意知,,,
∵,
∴,整理得,
故答案为:.
【点睛】本题考查了三角形内角和定理,三角形外角的性质,四边形内角和.解题的关键在于明确角度之间的数量关系.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个三角形中有两条边相等,则这个三角形是( )
A.不等边三角形 B.等边三角形 C.直角三角形 D.等腰三角形
2.将一张正方形的纸片减去一个角后,剩下纸片的角的个数为( )
A.5 B.3或4 C.4或5 D.3或4或5
3.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为( )
A.80° B.82° C.84° D.86°
4.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1、∠2、∠3、∠4对应的邻补角和等于215°,则∠BOD的度数为( )
A.30° B.35° C.40° D.45°
二、填空题
5.如图,正方形的边在正五边形的边上,则 .
6.如图,,,,则 .
7.如图所示,这是一个“星形”图案,则 .
8.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠CPD的度数是 .
三、解答题
9.如图,,,,求的度数.
10.如图所示,有一艘渔船上午九点在A处沿正东方向航行,在A处测得灯塔C在北偏东方向上,行驶到达B处,测得灯塔C在北偏东方向上,求的度数及的度数.
11.如图,若AB∥CD,EF与AB 、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠EFP的度数.
12.(1)如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC,且∠C大于∠B.求证:∠EAD=12(∠C-∠B).
(2)若把问题(1)中的“AD⊥BC于点D”改为“点F为EA上一点且FD⊥BC于点D”,画出新的图形,并说明∠EFD=12(∠C-∠B).
(3)若把问题(2)中的“F为EA上一点”改为“F为AE延长线上的一点”,则问题(2)中的结论成立吗?说明你的理由.
13.中,,点D,E分别是边上的点,点P是一动点.令,,.
(1)若点P在线段上,如图1所示,且,求的度数.
(2)若点P在边上运动,如图2所示,则,,之间有何关系?猜想并说明理由.
(3)若点P运动到边的延长线上,如图3所示,交于点M,,,之间的关系为__________.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查等腰三角形,根据至少有两边相等的三角形叫做等腰三角形,即可判断.
【详解】解:至少有两边相等的三角形叫做等腰三角形.
故选:D.
2.D
【分析】分三种情况,画出图形,即可得出结果.
【详解】解:如图,减去一个角有三种情况,
∴剩下纸片的角的个数为3或4或5;
故选D.
【点睛】本题主要考查了在不同情况下正方形的不同剪法,做此题考虑要全面不要遗漏,解答此题应根据题意,结合图形进行操作,进而得出结论.
3.A
【分析】根据三角形的内角和定理和三角形的外角性质即可解决.
【详解】解:∵∠BAC=105°,
∴∠2+∠3=75°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=75°,
∴∠2=25°.
∴∠DAC=105° 25°=80°.
故选A.
【点睛】此题主要考查了三角形的外角性质以及三角形内角和定理,熟记三角形的内角和定理,三角形的外角性质是解题的关键.
4.B
【分析】在DO延长线上找一点M,根据多边形AOEFG的外角和为360°可得出∠BOM=140°,再根据邻补角互补即可得出结论.
【详解】在DO延长线上找一点M,如图所示.
∵多边形AOEFG的外角和为360°,
∴∠BOM=360°-215°=145°.
∵∠BOD+∠BOM=180°,
∴∠BOD=180°-∠BOM=180°-145°=35°.
故选B.
【点睛】本题考查了多边形的内角与外角以及邻补角,解题的关键是根据多边形的外角和为360°找出∠BOM=145°.
5./18度
【分析】本题考查的知识点是正多边形的内角问题,解题关键是熟练掌握多边形内角和公式.
先根据多边形内角和公式求出五边形内角和和四边形内角和,再根据正多边形性质求出及,最后由即可求解.
【详解】解:根据多边形内角和计算公式可得:五边形内角和为,
四边形内角和为,
五边形是正五边形,
,
又正方形中,,
.
故答案为:.
6./100度
【分析】本题考查了三角形的外角的性质,熟练掌握三角形的外角性质是解题的关键;
根据三角形的外角性质求出,在根据得出、度数,再次利用三角形外角性质得,即可解答
【详解】,
,
,
,
,
,
故答案为:
7.
【分析】如图,连接,由题意知,,,则,同理可得,,由,可得,即.
【详解】解:如图,连接,
由题意知, ,,
∴,
同理可得,,
∵,
∴,
故答案为:.
【点睛】本题考查了三角形内角和定理,四边形内角和.解题的关键在于明确角度之间的数量关系.
8.60
【分析】根据五边形的内角和求出∠BCD和∠CDE的和,再根据角平分线及三角形内角和求出∠CPD.
【详解】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=540°﹣300°=240°,
∵∠BCD、∠CDE的平分线在五边形内相交于点O,
∴∠PDC+∠PCD=(∠BCD+∠CDE)=120°,
∴∠CPD=180°﹣120°=60°.
故答案是:60.
【点睛】本题解题的关键是知道多边形内角和定理以及角平分线的性质.
9.
【分析】本题考查三角形的外角,延长,交于点,先求出,再根据三角形的外角性质即可得出答案.
【详解】解:如图,延长,交于点.
,
.
,.
.
,,
.
10.45°;
【分析】本题考查的是与方位角的有关计算,三角形的内角和定理与三角形的外角的性质的应用,先由,可得,由,可得,再利用三角形的内角和定理与三角形的外角的性质可得答案.
【详解】解:∵在处测得灯塔在北偏东方向上,
∴,
∴.
∵行驶到达处,测得灯塔在北偏东方向上,
∴,
∴,
∴,
∴.
11.25°
【分析】由EP⊥EF,根据垂直的定义可得∠PEF=90°,根据∠BEF=∠BEP+∠PEF求得∠BEF的度数;又因AB∥CD,根据平行线的性质可得∠BEF+∠EFD=180°,从而求得∠EFD的度数,再由角平分线的定义可得∠EFP的度数,最后根据三角形的内角和定理求得∠EPF的度数.
【详解】解:∵EP⊥EF,∴∠PEF=90°.
∵∠BEP=50°,
∴∠BEF=∠BEP+∠PEF=140°.
∵AB∥CD,∴∠BEF+∠EFD=180°.
∴∠EFD=40°.
∵FP平分∠EFD,∴∠EFP=∠EFD=20°.
∵∠PEF+∠EFP+∠EPF=180°,
∴∠EPF=70°
12.(1)证明见解析; (2)理由见解析;(3)成立,理由见解析.
【详解】(1)在Rt△ADE中,
∵∠AED+∠DAE=90°,∴∠DAE=90°-∠AED.
∵∠AED=180°-∠C-∠CAE,且AE平分∠BAC,∴∠CAE= ∠BAC= (180°-∠C-∠B).∴∠EAD=90°-180°-∠C-1/2(180°-∠C-∠B)= (∠C-∠B).
(2)如图D11-2-5(1),由三角形的内角和定理的推论,得∠FED=∠B+ ∠BAC,故∠B+ ∠BAC+∠EFD=90°①.
在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即∠C+ ∠B+ ∠BAC=90°②.
②-①,得∠EFD= (∠C-∠B).
(3)成立.理由:如图D11-2-5(2),由三角形的内角和定理的推论,得∠FED=∠AEC=∠B+ ∠BAC,
故∠B+ ∠BAC+∠EFD=90°①.
在△ABC中,由三角形的内角和定理,得∠B+∠BAC+∠C=180°,即∠C+ ∠B+ ∠BAC=90°②.
②-①,得∠EFD= (∠C-∠B).
13.(1)的度数为;
(2)
(3)
【分析】(1)由题意知,,,由,可得,整理得,,将代入,计算求解即可;
(2)由(1)可知,;
(3)由题意知,,,由,可得,整理即可.
【详解】(1)解:由题意知,,,
∵,
∴,整理得,,
∵,
∴,
∴的度数为;
(2)解:,理由如下:
由(1)可知,;
(3)解:由题意知,,,
∵,
∴,整理得,
故答案为:.
【点睛】本题考查了三角形内角和定理,三角形外角的性质,四边形内角和.解题的关键在于明确角度之间的数量关系.
答案第1页,共2页
答案第1页,共2页
