八年级上册13.3.2等边三角形同步训练(含答案)
文档属性
| 名称 | 八年级上册13.3.2等边三角形同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 813.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 08:54:09 | ||
图片预览



文档简介
八年级上册 13.3.2 等边三角形 同步训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,将一个等边三角形剪去一个角后,等于( )
A.240° B.120° C.170° D.360°
2.下列对的判断,不正确的是( )
A.若,,则是等边三角形
B.若,则是直角三角形
C.若,则是等腰三角形
D.若,则
3.等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
A.90° B.100° C.120° D.无法确定
4.如图,在中,,,,点是边上的中点,点在BC上的一个动点,连接,在的下方作等边三角形,连接,则最小值是( )
A. B. C. D.
5.如图,点是线段上的一点,分别以、为边在直线的同侧作等边与等边,连接、分别交、于点、,与相交于点,连接.则下列结论中成立的有( ).
(1);(2);(3);(4)是等边三角形;(5).
A.2个 B.3个 C.4个 D.5个
二、填空题
6.小明同学将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件是 .
7.如图,是等边三角形,,于点D,则 .
8.如图,在等边中,,且,E是线段上的一个动点,连接,线段与线段关于直线对称,连接,在点E运动的过程中,当的长取得最小值时,的长为 .
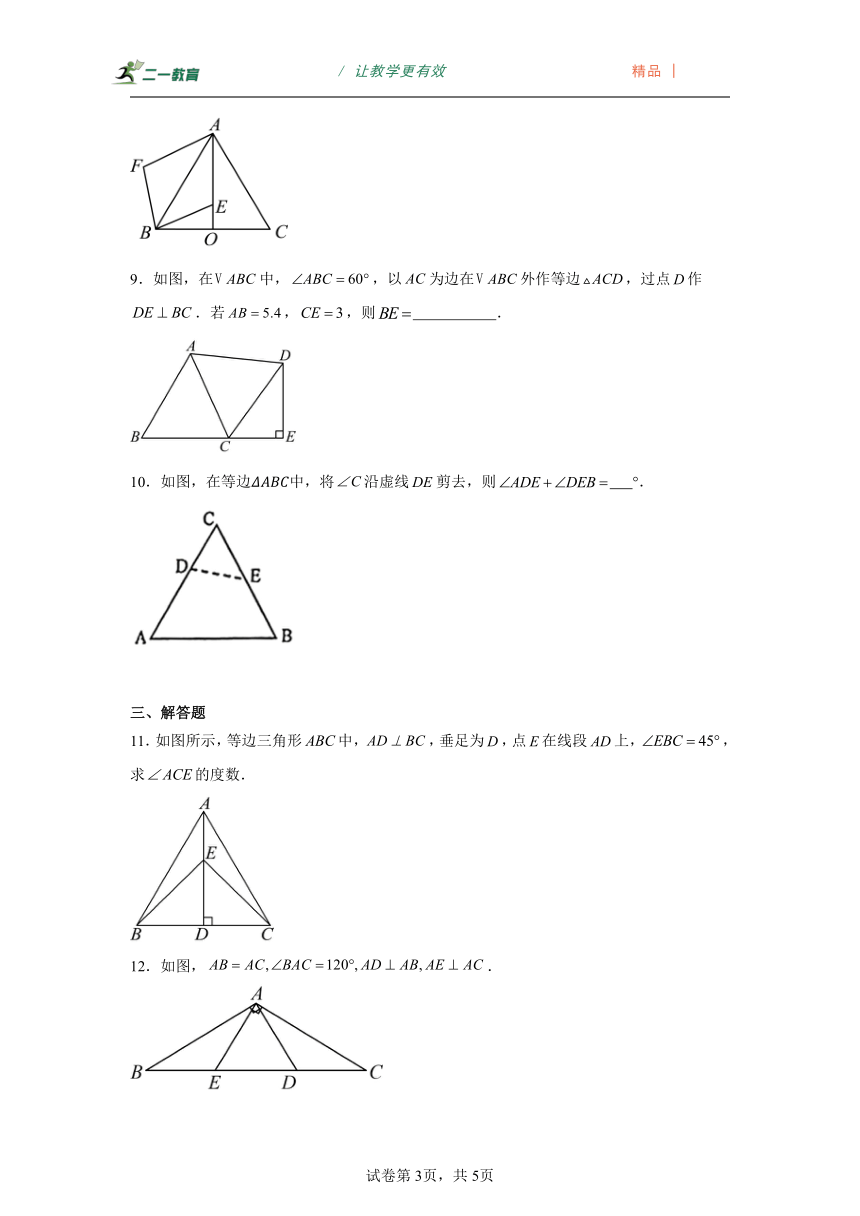
9.如图,在中,,以为边在外作等边,过点作.若,,则 .
10.如图,在等边中,将沿虚线剪去,则 °.
三、解答题
11.如图所示,等边三角形中,,垂足为,点在线段上,,求的度数.
12.如图,.
(1)在中, ______, ______;
(2)求证:是等边三角形.
13.如图,中,D为边上一点,的延长线交的延长线于F,且,.
(1)求证:是等腰三角形;
(2)当等于多少度时,是等边三角形?请证明你的结论.
14.如图,在中,,,点D是的中点,点E为边上一点,连接,,以为边在的左侧作等边三角形,连接.
(1)求证:为等边三角形;
(2)求证:.
15.如图1,在中,为线段上一动点(不与点B、C重合).连接,作,且,连接.
(1)求证:.
(2)当平分时,若,求的度数.
(3)如图2,设,在点D运动过程中,当时,__________°.(用含的式子表示)
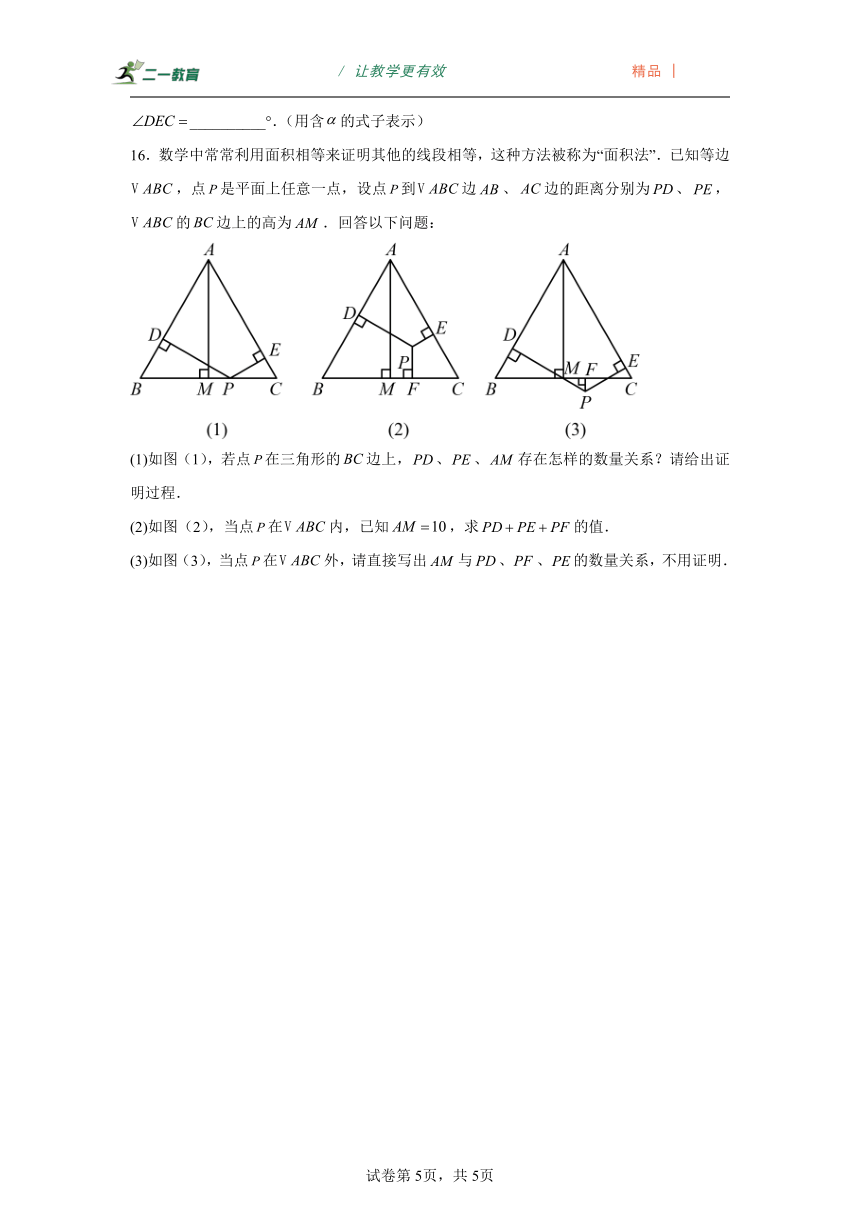
16.数学中常常利用面积相等来证明其他的线段相等,这种方法被称为“面积法”.已知等边,点是平面上任意一点,设点到边、边的距离分别为、,的边上的高为.回答以下问题:
(1)如图(1),若点在三角形的边上,、、存在怎样的数量关系?请给出证明过程.
(2)如图(2),当点在内,已知,求的值.
(3)如图(3),当点在外,请直接写出与、、的数量关系,不用证明.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.D
3.C
4.B
5.B
6.(答案不唯一)
7.2
8.1
9.7.8
10.240
11..
12.(1)解:∵,
∴,
∵,
∴,
∴;
故答案为:,2;
(2)由(1)知:,
∴,
∴是等边三角形.
13.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
∴,
∴是等腰三角形;
(2)解:当时,是等边三角形,证明如下:
∵,,
∴,
∵,
∴是等边三角形.
14.(1)证明:∵在中,,,
∴,,
又∵点D是的中点,
∴,
∴,
∴为等腰三角形,
又∵,
∴为等边三角形;
(2)证明:由(1)可知为等边三角形,
∴,
∵为等边三角形,
∴,
∴,
∴ ,
即,
在和中,
,
∴ ,
∴.
15.(1)证明,
∴
在和中
;
(2)由(1)可知,, ,
∴,
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴是等边三角形,
∴,
∴在中,;
(3),,
,
在和中
,
,
,
,
,
,
故答案为:.
16.(1)解:,
证明如下:连结,如图(1)所示:
设,
是等边三角形,
,
于点,于点,于点,
,,,
,
,
;
(2)解:连结、、,如图(2)所示:
设,
是等边三角形,
,
于点,于点,于点,于点,
,,,,
,
,
,
,
,
的值为;
(3)解:,
理由如下:连结、、,如图(3)所示:
设,
是等边三角形,
,
于点,于点,于点,于点,
,,,,
,
,
.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,将一个等边三角形剪去一个角后,等于( )
A.240° B.120° C.170° D.360°
2.下列对的判断,不正确的是( )
A.若,,则是等边三角形
B.若,则是直角三角形
C.若,则是等腰三角形
D.若,则
3.等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
A.90° B.100° C.120° D.无法确定
4.如图,在中,,,,点是边上的中点,点在BC上的一个动点,连接,在的下方作等边三角形,连接,则最小值是( )
A. B. C. D.
5.如图,点是线段上的一点,分别以、为边在直线的同侧作等边与等边,连接、分别交、于点、,与相交于点,连接.则下列结论中成立的有( ).
(1);(2);(3);(4)是等边三角形;(5).
A.2个 B.3个 C.4个 D.5个
二、填空题
6.小明同学将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件是 .
7.如图,是等边三角形,,于点D,则 .
8.如图,在等边中,,且,E是线段上的一个动点,连接,线段与线段关于直线对称,连接,在点E运动的过程中,当的长取得最小值时,的长为 .
9.如图,在中,,以为边在外作等边,过点作.若,,则 .
10.如图,在等边中,将沿虚线剪去,则 °.
三、解答题
11.如图所示,等边三角形中,,垂足为,点在线段上,,求的度数.
12.如图,.
(1)在中, ______, ______;
(2)求证:是等边三角形.
13.如图,中,D为边上一点,的延长线交的延长线于F,且,.
(1)求证:是等腰三角形;
(2)当等于多少度时,是等边三角形?请证明你的结论.
14.如图,在中,,,点D是的中点,点E为边上一点,连接,,以为边在的左侧作等边三角形,连接.
(1)求证:为等边三角形;
(2)求证:.
15.如图1,在中,为线段上一动点(不与点B、C重合).连接,作,且,连接.
(1)求证:.
(2)当平分时,若,求的度数.
(3)如图2,设,在点D运动过程中,当时,__________°.(用含的式子表示)
16.数学中常常利用面积相等来证明其他的线段相等,这种方法被称为“面积法”.已知等边,点是平面上任意一点,设点到边、边的距离分别为、,的边上的高为.回答以下问题:
(1)如图(1),若点在三角形的边上,、、存在怎样的数量关系?请给出证明过程.
(2)如图(2),当点在内,已知,求的值.
(3)如图(3),当点在外,请直接写出与、、的数量关系,不用证明.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.D
3.C
4.B
5.B
6.(答案不唯一)
7.2
8.1
9.7.8
10.240
11..
12.(1)解:∵,
∴,
∵,
∴,
∴;
故答案为:,2;
(2)由(1)知:,
∴,
∴是等边三角形.
13.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
∴,
∴是等腰三角形;
(2)解:当时,是等边三角形,证明如下:
∵,,
∴,
∵,
∴是等边三角形.
14.(1)证明:∵在中,,,
∴,,
又∵点D是的中点,
∴,
∴,
∴为等腰三角形,
又∵,
∴为等边三角形;
(2)证明:由(1)可知为等边三角形,
∴,
∵为等边三角形,
∴,
∴,
∴ ,
即,
在和中,
,
∴ ,
∴.
15.(1)证明,
∴
在和中
;
(2)由(1)可知,, ,
∴,
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,
∴是等边三角形,
∴,
∴是等边三角形,
∴,
∴在中,;
(3),,
,
在和中
,
,
,
,
,
,
故答案为:.
16.(1)解:,
证明如下:连结,如图(1)所示:
设,
是等边三角形,
,
于点,于点,于点,
,,,
,
,
;
(2)解:连结、、,如图(2)所示:
设,
是等边三角形,
,
于点,于点,于点,于点,
,,,,
,
,
,
,
,
的值为;
(3)解:,
理由如下:连结、、,如图(3)所示:
设,
是等边三角形,
,
于点,于点,于点,于点,
,,,,
,
,
.
答案第1页,共2页
答案第1页,共2页
