优课沪科版(新)初中数学九年级上第22章22.2相似三角形的判定课件(共23张PPT)
文档属性
| 名称 | 优课沪科版(新)初中数学九年级上第22章22.2相似三角形的判定课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 937.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-31 00:00:00 | ||
图片预览






文档简介
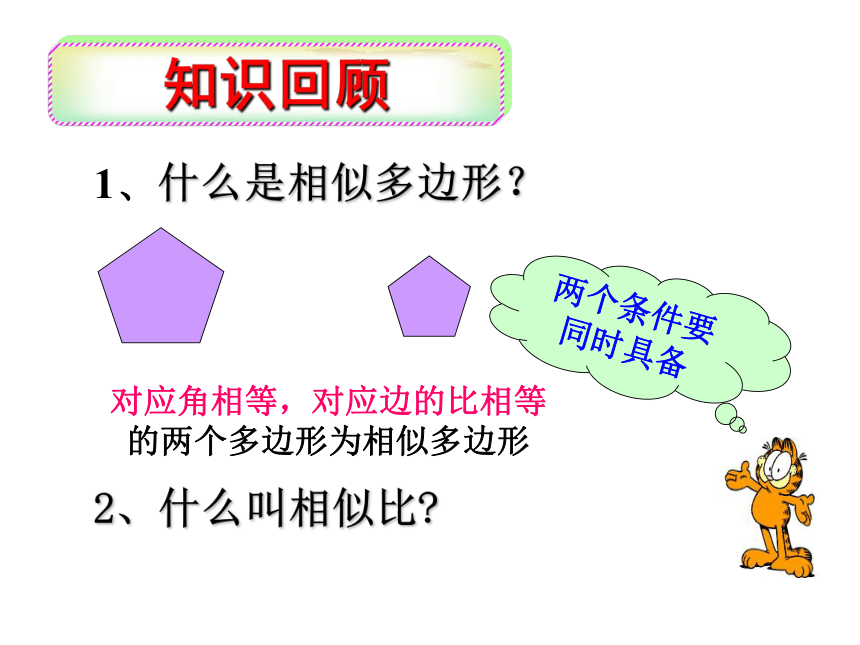
课件23张PPT。相似三角形的判定知识回顾1、什么是相似多边形?2、什么叫相似比?对应角相等,对应边的比相等
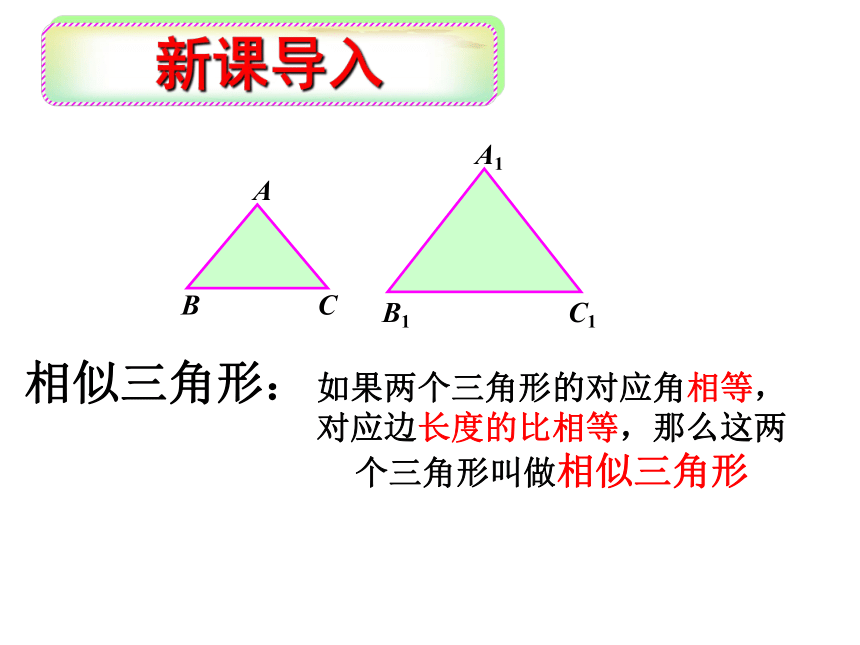
的两个多边形为相似多边形两个条件要同时具备新课导入相似三角形:如果两个三角形的对应角相等,对应边长度的比相等,那么这两个三角形叫做相似三角形
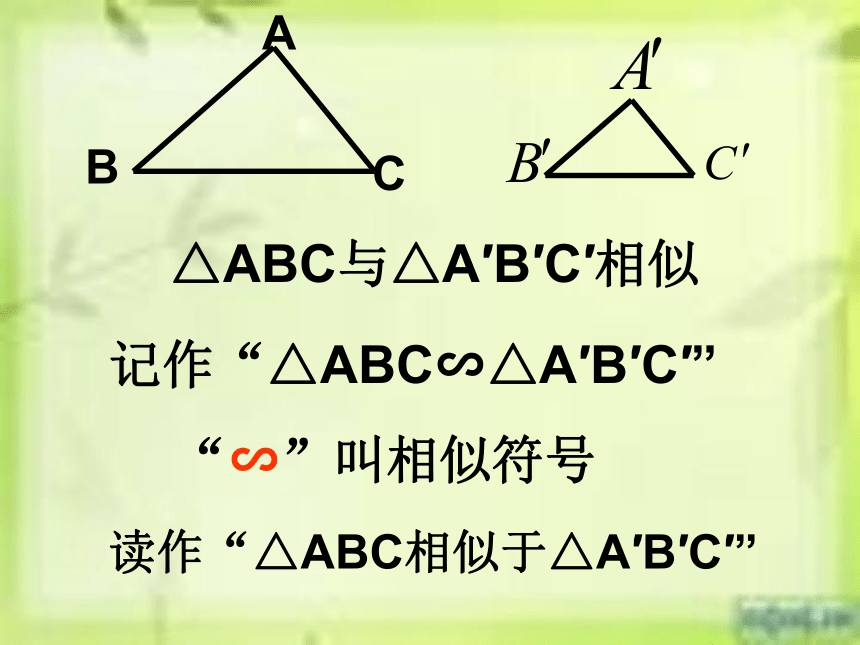
△ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”“∽”叫相似符号读作“△ABC相似于△A′B′C′”小提示:两个三角形相似,用字母表示时与全等一样,应把表示对应顶点的字母写在对应位置上,这样便于找出相似三角形的对应角与对应边对于△ABC∽△A′B′C′
根据相似形的定义,应有
∠A=∠A′,∠B=∠B′,∠C=∠C′
相似三角形的对应关系:相似比思考:当k=1的时候,两个三角形还有怎样的关系?相似比当k=1的时候, 则所以
已知△ABC∽△DEF,请指出所有的对应边和对应角.并分别指出它们的关系.练一练:想一想:它们的对应角,对应边各有什么关系时可以判定这两个三角形相似呢?相似三角形的判定定义判定:对应角相等,对应边成比例的两个三角形相似.符号语言:在△ABC和△A′B′C′中,∵∴△ABC∽△A′B′C′探究论证:在△ABC中,D为AB上任意一点,
如图所示.过点D作BC的平行线交AC于点E,
那么△ADE与△ABC相似吗? 由已知和图2可知△ADE与△ABC相似必须有:∠A=∠A,∠ADE=∠B, ∠ AED=∠C,
分析: 1.根据相似形的定义△ADE与 △ABC相似必须满足哪些条件?图22.已经具备哪些条件?为什么?还需要什么条件?已有条件:∠A=∠A,∠ADE=∠B, ∠AED=∠C ,
还需要条件:
3.解决这个问题的关键在哪里?怎么解决? 转化:将DE平移到BC上(可过D点作DF∥AC交BC于点F,则CF=DE)运用定理:平行于三角形一边的直线截其他两边(或两边延长线),所得对应线段成比例。即可得到
ADEBCF如果这条直线与三角形两边的延长线相交呢? 由以上探究过程你能得出什么结论?归纳: 符号语言
在△ABC中,
若 DE∥BC,(如图3所示)
则 △ADE∽△ABC.
平行于三角形一边的直线与其他两边(或两边的 )相交,定理:截得的三角形与 形相似延长线原三角DE∥BC△ADE∽△ ABC“A”型“x”型思考相似具有传递性△ADE∽△ABCMN 如果再作 MN∥DE ,共有多少对相似三角形?△AMN∽△ADE△AMN∽△ABC共有三对相似三角形。已知DE∥BC
如图4,在 ABCD中,DE交BC于F,交AB的延长线于点E.(1)请写出图中相似的三角形;(2)由其中的一对相似三角形写出相应的比例式;(3)请说明AE·BF与AD·BE小试牛刀:是否相等?丰收园本节课你有什么收获?还有什么疑惑?作业:
课本中本节练习
的两个多边形为相似多边形两个条件要同时具备新课导入相似三角形:如果两个三角形的对应角相等,对应边长度的比相等,那么这两个三角形叫做相似三角形
△ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”“∽”叫相似符号读作“△ABC相似于△A′B′C′”小提示:两个三角形相似,用字母表示时与全等一样,应把表示对应顶点的字母写在对应位置上,这样便于找出相似三角形的对应角与对应边对于△ABC∽△A′B′C′
根据相似形的定义,应有
∠A=∠A′,∠B=∠B′,∠C=∠C′
相似三角形的对应关系:相似比思考:当k=1的时候,两个三角形还有怎样的关系?相似比当k=1的时候, 则所以
已知△ABC∽△DEF,请指出所有的对应边和对应角.并分别指出它们的关系.练一练:想一想:它们的对应角,对应边各有什么关系时可以判定这两个三角形相似呢?相似三角形的判定定义判定:对应角相等,对应边成比例的两个三角形相似.符号语言:在△ABC和△A′B′C′中,∵∴△ABC∽△A′B′C′探究论证:在△ABC中,D为AB上任意一点,
如图所示.过点D作BC的平行线交AC于点E,
那么△ADE与△ABC相似吗? 由已知和图2可知△ADE与△ABC相似必须有:∠A=∠A,∠ADE=∠B, ∠ AED=∠C,
分析: 1.根据相似形的定义△ADE与 △ABC相似必须满足哪些条件?图22.已经具备哪些条件?为什么?还需要什么条件?已有条件:∠A=∠A,∠ADE=∠B, ∠AED=∠C ,
还需要条件:
3.解决这个问题的关键在哪里?怎么解决? 转化:将DE平移到BC上(可过D点作DF∥AC交BC于点F,则CF=DE)运用定理:平行于三角形一边的直线截其他两边(或两边延长线),所得对应线段成比例。即可得到
ADEBCF如果这条直线与三角形两边的延长线相交呢? 由以上探究过程你能得出什么结论?归纳: 符号语言
在△ABC中,
若 DE∥BC,(如图3所示)
则 △ADE∽△ABC.
平行于三角形一边的直线与其他两边(或两边的 )相交,定理:截得的三角形与 形相似延长线原三角DE∥BC△ADE∽△ ABC“A”型“x”型思考相似具有传递性△ADE∽△ABCMN 如果再作 MN∥DE ,共有多少对相似三角形?△AMN∽△ADE△AMN∽△ABC共有三对相似三角形。已知DE∥BC
如图4,在 ABCD中,DE交BC于F,交AB的延长线于点E.(1)请写出图中相似的三角形;(2)由其中的一对相似三角形写出相应的比例式;(3)请说明AE·BF与AD·BE小试牛刀:是否相等?丰收园本节课你有什么收获?还有什么疑惑?作业:
课本中本节练习
