2.2.4均值不等式及其应用--2024-2025学年高一数学人教B版(2019)必修第一册同步课时训练(含解析)
文档属性
| 名称 | 2.2.4均值不等式及其应用--2024-2025学年高一数学人教B版(2019)必修第一册同步课时训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 357.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 12:50:14 | ||
图片预览



文档简介
2.2.4 均值不等式及其应用--2024-2025学年高一数学人教B版(2019)必修第一册同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知,,且,则ab的最小值为( )
A.100 B.81 C.36 D.9
2.当时,的最小值为( )
A. B.1 C.2 D.
3.已知实数x,y满足,且,若不等式恒成立,则实数t的最大值为( )
A.4 B.-4 C. D.
4.已知,,且,则的最小值为( )
A.1 B.2 C.4 D.8
5.已知a,b为正实数,且,则的最小值为( )
A.3 B.4 C.5 D.6
6.若,则的最小值是( )
A. B. C. D.
7.已知a,b为正实数,且满足,则的最小值为( )
A. B. C.8 D.6
8.已知实数x,y,z不全为0,则的最大值为( )
A. B. C. D.
二、多项选择题
9.某公司一年购买某种货物吨,现分次购买,设每次购买x吨,运费为8万元/次.已知一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和y最小,则下列说法正确的是( )
A.当时,y取得最小值
B.当时,y取得最小值
C.
D.
10.下列结论正确的是( )
A.设,则的最小值是 B.当时,的最小值是2
C.当时, D.当时,的最大值是1
三、填空题
11.已知实数x,,且,则的最小值是________.
12.某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是__________.
13.已知,,且,则的最小值是____________.
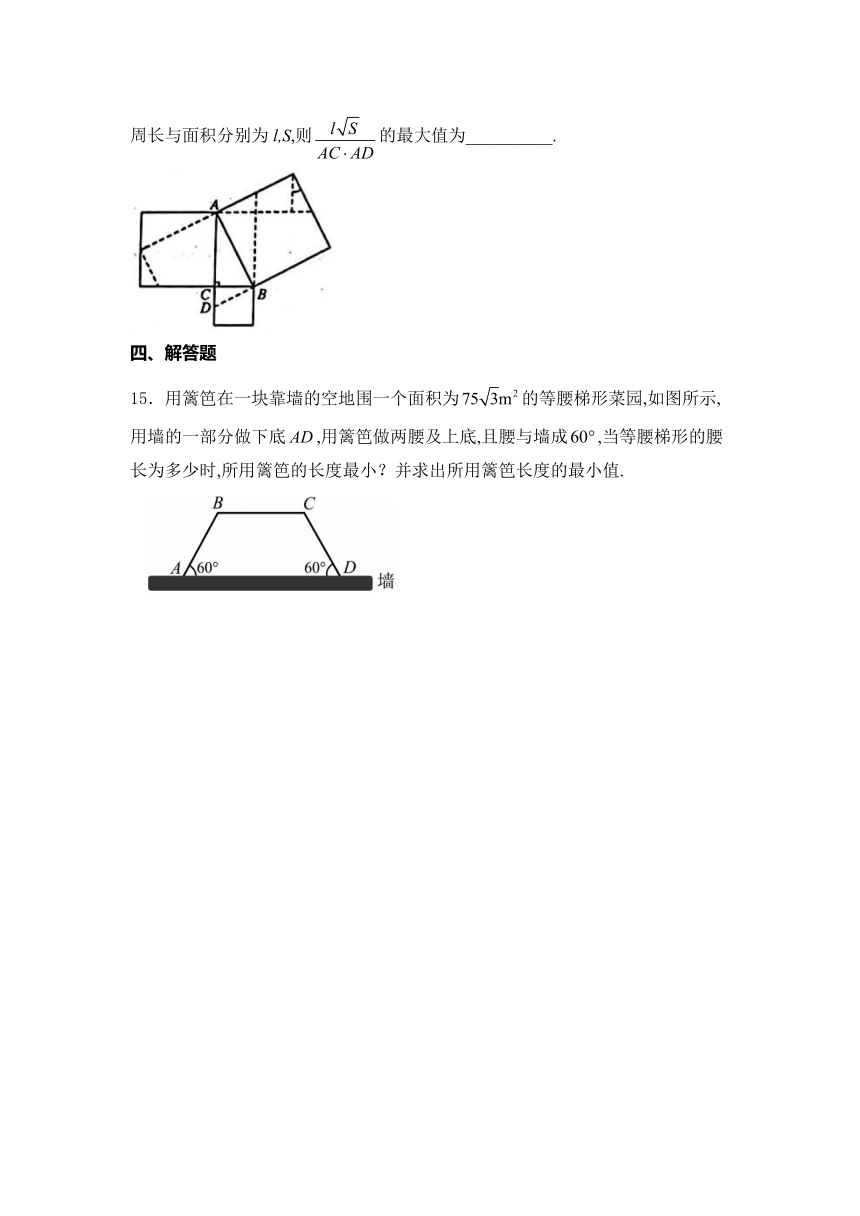
14.我国后汉时期的数学家赵爽通过弦图利用出入相补法证明了勾股定理,在我国历史上还有多人通过出入相补法证明过勾股定理,如下图为我国清末数学家华蘅芳证明勾股定理时构造的图形,在该图中是以AB为斜边的直角三角形,分别以AB,BC,AC为边作3个正方形,点D在直线AC上,,记的周长与面积分别为l,S,则的最大值为__________.
四、解答题
15.用篱笆在一块靠墙的空地围一个面积为的等腰梯形菜园,如图所示,用墙的一部分做下底,用篱笆做两腰及上底,且腰与墙成,当等腰梯形的腰长为多少时,所用篱笆的长度最小?并求出所用篱笆长度的最小值.
参考答案
1.答案:C
解析:因为,,
所以,当且仅当,即,取等号,
所以,所以ab的最小值为36,
故选:C
2.答案:C
解析:,当且仅当时,等号成立,故的最小值为2.故选C.
3.答案:A
解析:因为,
,当且仅当且即时取等号,此时取得最小值,
由恒成立,故即t的最大值4.
故选:A.
4.答案:C
解析:因为,
所以,
所以,所以,
当且仅当时取等号,
所以的最小值为4.
故选:C.
5.答案:B
解析:因为a,b为正实数,且,
所以,
当且仅当等号成立.
故选:B.
6.答案:B
解析:由,可得,
,
当且仅当,即 时取等号,
所以的最小值为.
故选:B.
7.答案:C
解析:根据题意,
当且仅当,即时,等号成立.
故选:C
8.答案:D
解析:由题意实数x,y,z不全为0,
,
当且仅当时,等号成立.
故选:D.
9.答案:AC
解析:一年购买某种货物吨,每次购买x吨,则需要购买次,又运费是8万元/次,一年的总存储费用为4x万元,
所以一年的总运费与总存储费用之和万元.
因为,当且仅当,即时,等号成立,
所以当时,y取得最小值,.
故选:AC.
10.答案:CD
解析:对于选项A:不是定值,不是的最小值,故选项A错误;
对于选项B:当时,由基本不等式可得,当且仅当,即时取等号,但,故取不到等号,故2不是的最小值,故选项B错误;
对于选项C:当时,由基本不等式可得,当且仅当,即时,等号成立,故选项C正确;
对于选项D:当,即时,
,
当且仅当,即时等号成立,故选项D正确.
故选:CD.
11.答案:
解析:,,且,
,
,
当且仅当,即,时取等号,
的最小值是,
故答案为:.
12.答案:30
解析:设总费用为y万元,则,当且仅当,即时,等号成立.
13.答案:
解析:由题意可得,
则.
因为,,所以,
当且仅当时,等号成立,则.
故答案为:.
14.答案:
解析:设,,则,由,,
易得,
所以,当且仅当时取等号,所以的最大值为.
15.答案:等腰梯形的腰长为时,所用篱笆长度最小,其最小值为
解析:设,上底,
分别过点B,C作下底的垂线,垂足分别为E,F,
则,,
则下底,
该等腰梯形的面积,
所以,则,
所用篱笆长为
,
当且仅当,即,时取等号.
所以,当等腰梯形的腰长为时,所用篱笆长度最小,其最小值为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知,,且,则ab的最小值为( )
A.100 B.81 C.36 D.9
2.当时,的最小值为( )
A. B.1 C.2 D.
3.已知实数x,y满足,且,若不等式恒成立,则实数t的最大值为( )
A.4 B.-4 C. D.
4.已知,,且,则的最小值为( )
A.1 B.2 C.4 D.8
5.已知a,b为正实数,且,则的最小值为( )
A.3 B.4 C.5 D.6
6.若,则的最小值是( )
A. B. C. D.
7.已知a,b为正实数,且满足,则的最小值为( )
A. B. C.8 D.6
8.已知实数x,y,z不全为0,则的最大值为( )
A. B. C. D.
二、多项选择题
9.某公司一年购买某种货物吨,现分次购买,设每次购买x吨,运费为8万元/次.已知一年的总存储费用为4x万元,要使一年的总运费与总存储费用之和y最小,则下列说法正确的是( )
A.当时,y取得最小值
B.当时,y取得最小值
C.
D.
10.下列结论正确的是( )
A.设,则的最小值是 B.当时,的最小值是2
C.当时, D.当时,的最大值是1
三、填空题
11.已知实数x,,且,则的最小值是________.
12.某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是__________.
13.已知,,且,则的最小值是____________.
14.我国后汉时期的数学家赵爽通过弦图利用出入相补法证明了勾股定理,在我国历史上还有多人通过出入相补法证明过勾股定理,如下图为我国清末数学家华蘅芳证明勾股定理时构造的图形,在该图中是以AB为斜边的直角三角形,分别以AB,BC,AC为边作3个正方形,点D在直线AC上,,记的周长与面积分别为l,S,则的最大值为__________.
四、解答题
15.用篱笆在一块靠墙的空地围一个面积为的等腰梯形菜园,如图所示,用墙的一部分做下底,用篱笆做两腰及上底,且腰与墙成,当等腰梯形的腰长为多少时,所用篱笆的长度最小?并求出所用篱笆长度的最小值.
参考答案
1.答案:C
解析:因为,,
所以,当且仅当,即,取等号,
所以,所以ab的最小值为36,
故选:C
2.答案:C
解析:,当且仅当时,等号成立,故的最小值为2.故选C.
3.答案:A
解析:因为,
,当且仅当且即时取等号,此时取得最小值,
由恒成立,故即t的最大值4.
故选:A.
4.答案:C
解析:因为,
所以,
所以,所以,
当且仅当时取等号,
所以的最小值为4.
故选:C.
5.答案:B
解析:因为a,b为正实数,且,
所以,
当且仅当等号成立.
故选:B.
6.答案:B
解析:由,可得,
,
当且仅当,即 时取等号,
所以的最小值为.
故选:B.
7.答案:C
解析:根据题意,
当且仅当,即时,等号成立.
故选:C
8.答案:D
解析:由题意实数x,y,z不全为0,
,
当且仅当时,等号成立.
故选:D.
9.答案:AC
解析:一年购买某种货物吨,每次购买x吨,则需要购买次,又运费是8万元/次,一年的总存储费用为4x万元,
所以一年的总运费与总存储费用之和万元.
因为,当且仅当,即时,等号成立,
所以当时,y取得最小值,.
故选:AC.
10.答案:CD
解析:对于选项A:不是定值,不是的最小值,故选项A错误;
对于选项B:当时,由基本不等式可得,当且仅当,即时取等号,但,故取不到等号,故2不是的最小值,故选项B错误;
对于选项C:当时,由基本不等式可得,当且仅当,即时,等号成立,故选项C正确;
对于选项D:当,即时,
,
当且仅当,即时等号成立,故选项D正确.
故选:CD.
11.答案:
解析:,,且,
,
,
当且仅当,即,时取等号,
的最小值是,
故答案为:.
12.答案:30
解析:设总费用为y万元,则,当且仅当,即时,等号成立.
13.答案:
解析:由题意可得,
则.
因为,,所以,
当且仅当时,等号成立,则.
故答案为:.
14.答案:
解析:设,,则,由,,
易得,
所以,当且仅当时取等号,所以的最大值为.
15.答案:等腰梯形的腰长为时,所用篱笆长度最小,其最小值为
解析:设,上底,
分别过点B,C作下底的垂线,垂足分别为E,F,
则,,
则下底,
该等腰梯形的面积,
所以,则,
所用篱笆长为
,
当且仅当,即,时取等号.
所以,当等腰梯形的腰长为时,所用篱笆长度最小,其最小值为.
