优课沪科版(新)初中数学九年级上第23章23.2解直角三角形及其应用课件(共13张PPT)
文档属性
| 名称 | 优课沪科版(新)初中数学九年级上第23章23.2解直角三角形及其应用课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-31 00:00:00 | ||
图片预览




文档简介
课件13张PPT。23.2 解直角三角形及其应用解直角三角形的原则:(1) 有角先求角 无角先求边
(2) 有斜用弦, 无斜用切;
(3) 能乘勿除, 取原避中。知识点 知识点1
解直角三角形的依据(1)三边之间的关系
(2)边角之间的关系
(3)锐角之间的关系
知识点2
仰角:水平线与在它上方的视线所成的角.
俯角:水平线与在它下方的视线所成的角
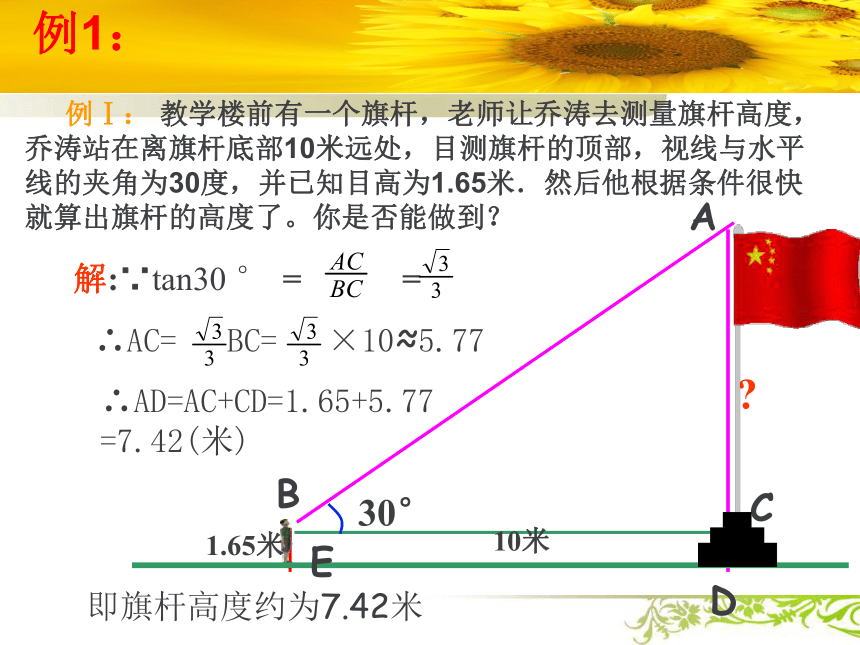
例Ⅰ: 教学楼前有一个旗杆,老师让乔涛去测量旗杆高度,乔涛站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他根据条件很快就算出旗杆的高度了。你是否能做到??CD 解:∵tan30 ° = =∴AC= BC= ×10≈5.77∴AD=AC+CD=1.65+5.77=7.42(米)即旗杆高度约为7.42米例1:练习1:
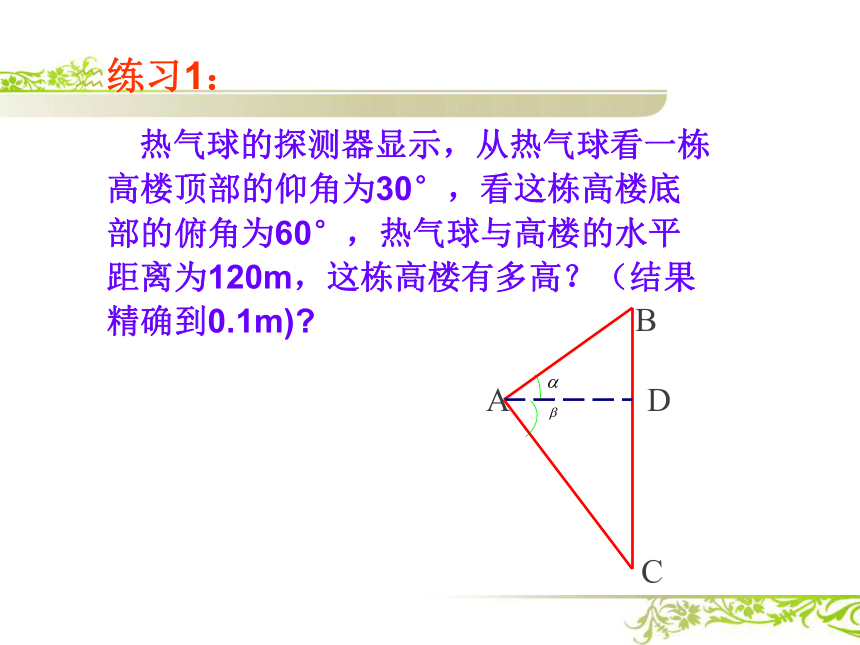
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果精确到0.1m)?
解:在Rt△ADB中,
BD=AD =120× ≈69.3(m)
在Rt △ADC中,tanβ=
DC=ADtan60°=120 ≈207.8(m)
∴BC=BD+DC=69.3+207.8=277.1(m)
答:这栋楼高277.1m。
练习2:
如图,B、C是河对岸的两点,A是岸边边上的一点,测得∠ABC=∠ACB=45°,BC=60米,则点A到BC的距离为 。30米例2:海上有一座灯塔P,在它周围3海里内有暗礁,一艘客轮以每小时9海里的速度由西向东航行,行至A处测得灯塔P在它的北偏东60°,继续行驶20分钟后,到达B处,又测得灯塔P在它的北偏东45°,问客轮不改变方向,继续前进有无触礁的危险?ABP 解:过P点作PD垂直于AB,交AB的延长线于D ∴ ∠PAD=30°,∠PBD=45°在Rt△BDP中,∴ BD = PDAB = 9 ×20÷60 = 3海里设BD=PD= x海里∴ AD =( 3+x)海里tan A=在Rt△ADP中x = AD · tan30° PD = x > 3∴ 无 触 礁 危 险∠PBD=45° 60°45°xxD12 练习3: 某海滨浴场的沿岸可以看成直线,如图,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑了300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是每秒6米,在水中游泳的速度都是每秒2米,∠BAD=45°请你解决下面问题。
(1)请问1号救生员的做法是否合理?
(2)若2号救生员从A跑到C,再跳水入海中游泳到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1)
sin65°≈0.9,cos65°≈0.4,tan65°≈2.0,√2≈1.4
解(1)在Rt△ADB中,∵∠A=45° ∴∠ABD=45 ° ∴BD=AD=300米
∴ 即:
(2)在Rt△BCD中,BC= = ≈333.3m
CD= = =150m
∴AC=AD-CD=300-150=150m
秒
因为 ,所以(1)不合理。小结
解直角三角形在几何中的应用,关键是通过作垂线的方法,合理地构造出将已知元素和未知元素包含在内的直角三角形,分析已知量与未知量在这个三角形中的联系。 2、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离. 作业:
1、某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.
(2) 有斜用弦, 无斜用切;
(3) 能乘勿除, 取原避中。知识点 知识点1
解直角三角形的依据(1)三边之间的关系
(2)边角之间的关系
(3)锐角之间的关系
知识点2
仰角:水平线与在它上方的视线所成的角.
俯角:水平线与在它下方的视线所成的角
例Ⅰ: 教学楼前有一个旗杆,老师让乔涛去测量旗杆高度,乔涛站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他根据条件很快就算出旗杆的高度了。你是否能做到??CD 解:∵tan30 ° = =∴AC= BC= ×10≈5.77∴AD=AC+CD=1.65+5.77=7.42(米)即旗杆高度约为7.42米例1:练习1:
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果精确到0.1m)?
解:在Rt△ADB中,
BD=AD =120× ≈69.3(m)
在Rt △ADC中,tanβ=
DC=ADtan60°=120 ≈207.8(m)
∴BC=BD+DC=69.3+207.8=277.1(m)
答:这栋楼高277.1m。
练习2:
如图,B、C是河对岸的两点,A是岸边边上的一点,测得∠ABC=∠ACB=45°,BC=60米,则点A到BC的距离为 。30米例2:海上有一座灯塔P,在它周围3海里内有暗礁,一艘客轮以每小时9海里的速度由西向东航行,行至A处测得灯塔P在它的北偏东60°,继续行驶20分钟后,到达B处,又测得灯塔P在它的北偏东45°,问客轮不改变方向,继续前进有无触礁的危险?ABP 解:过P点作PD垂直于AB,交AB的延长线于D ∴ ∠PAD=30°,∠PBD=45°在Rt△BDP中,∴ BD = PDAB = 9 ×20÷60 = 3海里设BD=PD= x海里∴ AD =( 3+x)海里tan A=在Rt△ADP中x = AD · tan30° PD = x > 3∴ 无 触 礁 危 险∠PBD=45° 60°45°xxD12 练习3: 某海滨浴场的沿岸可以看成直线,如图,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑了300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是每秒6米,在水中游泳的速度都是每秒2米,∠BAD=45°请你解决下面问题。
(1)请问1号救生员的做法是否合理?
(2)若2号救生员从A跑到C,再跳水入海中游泳到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1)
sin65°≈0.9,cos65°≈0.4,tan65°≈2.0,√2≈1.4
解(1)在Rt△ADB中,∵∠A=45° ∴∠ABD=45 ° ∴BD=AD=300米
∴ 即:
(2)在Rt△BCD中,BC= = ≈333.3m
CD= = =150m
∴AC=AD-CD=300-150=150m
秒
因为 ,所以(1)不合理。小结
解直角三角形在几何中的应用,关键是通过作垂线的方法,合理地构造出将已知元素和未知元素包含在内的直角三角形,分析已知量与未知量在这个三角形中的联系。 2、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离. 作业:
1、某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.
