人教版九年级上册数学第二十一章一元二次方程综单元试题(含解析)
文档属性
| 名称 | 人教版九年级上册数学第二十一章一元二次方程综单元试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 16:08:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十一章一元二次方程综单元试题
一、单选题(每题3分,共30分)
1.下列方程中,是一元二次方程的是( )
A. B.
C. D.
2.若关于x的方程的一个根为3,则m的值为( )
A.3 B. C.4 D.
3.已知,是一元二次方程的两个根,则的值是( )
A.4 B. C. D.2
4.近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为21万元,5月份售价为18万元.设该款汽车这两月售价的月均下降率是x,则所列方程正确的是( )
A. B. C. D.
5.关于方程的根的说法中,正确的是( )
A.没有实数根 B.有两个不相等的实数根
C.两个实数根的和为2 D.两个实数根的积为-3
6.若关于x的一元二次方程两根为、,且,则p的值为( )
A. B. C. D.6
7.若一元二次方程的根判别式的值为,则的值为( )
A.1 B. C.3 D.
8.关于的一元二次方程的两个实数根分别为2和,则分解因式等于( )
A. B. C. D.
9.为推进节能减排,创建低碳绿色城市,学校计划植一批樟树,第一个月植树100棵,第三个月植树400棵,设植树月平均增长率为x,根据题意,请列出方程( )
A. B.
C. D.
10.设,是关于x的一元二次方程的两个实数根,且,则m的值为( )
A.2 B.4 C.2或 D.或4
二、填空题(每题3分,共30分)
11.关于的方程有实数根,则的取值范围为 .
12.已知关于x的一元二次方程有两个相等的实数根,则a的值为 .
13.某乡镇年旅游总收入为万元,到年旅游总收入达万元.若每年的平均增长率相同,则年平均增长率是 .
14.若方程有一个解为,则方程的解为 .
15.若m是方程的一个实数根,则代数式的值为 .
16.方程的一次项系数是,二次项系数是 2,常数项是 .
17.在解方程时,小王看错了m,解得方程的根为6与;小李看错了n,解得方程的根为2与,则原方程的解为 .
18.已知关于x的一元二次方程有两个不相等的实数根,则实数k的取值范围是 .
19.设、是一元二次方程的两个根,且,则 .
20.某超市一月份的营业额为200万元,第一季度总营业额为800万元,设平均每月营业额的增长率为x,则由题意列方程为 .
三、解答题(共60分)
21.解方程:
(1); (2).
22.已知:,是关于的一元二次方程的两个根.
(1)若,求的值;
(2)在(1)的条件下,求的值.
23.已知关于x的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若该方程的两个实数根都是整数,且其中一个根是另一个根的3倍,求a的值.
24.在课外活动中,小华根据学习平行四边形、菱形、正方形的经验对其面积进行了研究.他将一根长为的小棒截成两段,并将之放置在互相垂直平分的位置上,将端点用橡皮筋连接,即构造出了菱形.
(1)若所构菱形面积为,则应如何截取?
(2)所构菱形面积可以为吗?试说明理由.
25.某芯片公司引进了一条内存芯片生产线,开工第一个月生产80万个,第三个月生产96.8万个.
(1)已知每个月生产量的增长率相等,求前三个月生产量的月增长率;
(2)经调查发现,1条生产线最大产能是150万个/月,若每增加1条生产线,每条生产线的最大产能将减少6万个/月,现该公司要保证每月生产内存芯片528万个,在增加产能同时又要节省投入成本的条件下(生产线越多,投入成本越大),应该再增加几条生产线?
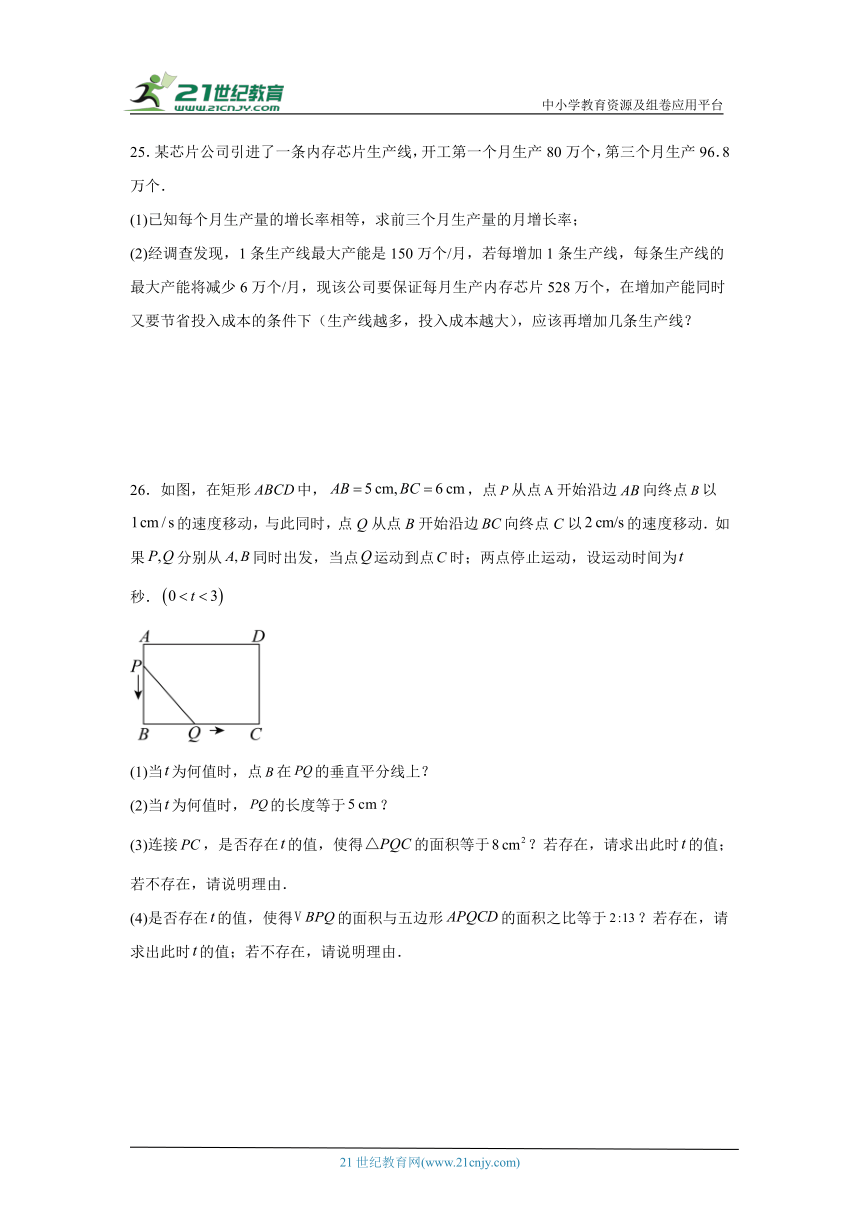
26.如图,在矩形中,,点从点开始沿边向终点以的速度移动,与此同时,点Q从点B开始沿边向终点C以的速度移动.如果分别从同时出发,当点运动到点时;两点停止运动,设运动时间为秒.
(1)当为何值时,点在的垂直平分线上?
(2)当为何值时,的长度等于?
(3)连接,是否存在的值,使得的面积等于?若存在,请求出此时的值;若不存在,请说明理由.
(4)是否存在的值,使得的面积与五边形的面积之比等于?若存在,请求出此时的值;若不存在,请说明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】本题主要考查了一元二次方程的定义,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
根据一元二次方程的定义逐个分析即可解答:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
【详解】解:A、中含有两个未知数,故不是一元二次方程,不合题意;
B、是分式方程,不符合题意;
C、是无理方程,故不是一元二次方程,不合题意;
D、是一元二次方程,符合题意.
故选:B.
2.C
【分析】本题主要考查了一元二次方程的解,将代入,解关于m的方程即可.
【详解】解:将代入,得:,
解得,
故选C.
3.D
【分析】本题考查了一元二次方程的根与系数关系,根据根与系数关系可得,,代入即可解答.
【详解】解:∵是一元二次方程,即的两个实数根,
∴,,
∴.
故选:D
4.D
【分析】此题主要考查了一元二次方程的应用.首先根据3月份售价为21万元,月均下降率是可得出4月份的售价为万元,5月份的售价为万元,据此根据5月份售价为18万元可列出方程,进而可得出答案.
【详解】解:月份售价为21万元,月均下降率是,5月份售价为18万元,
.
故选:D.
5.B
【分析】此题考查了一元二次方程根的判别式,先求出一元二次方程根的判别式的值,再根据判别式的值即可得到答案.
【详解】解:对于方程,
∵,
∴,
∴方程有两个不相等的实数根,
故选:B
6.A
【分析】本题考查了一元二次方程根与系数的关系:若方程的两实数根为,则.
根据一元二次方程根与系数的关系得到,然后通分,,从而得到关于p的方程,解方程即可.
【详解】解:,
,
而,
,
,
故选:A.
7.B
【分析】本题考查了一元二次方程根的判别式;利用一元二次方程根的判别式即可解决问题.
【详解】解:因为一元二次方程的根判别式的值为,
所以,
解得.
故选:B.
8.C
【分析】本题考查了一元二次方程根的性质,由题意得出方程可以化为,即可得出答案.
【详解】解:∵关于的一元二次方程的两个实数根分别为2和,
∴方程可以化为,
∴,
故选:C.
9.B
【分析】利用第三个月该植树棵数第一个月该校植树棵数该校植树棵数的年平均增长率),即可列出关于的一元二次方程,此题得解.本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
【详解】解:∵第一个月植树100棵,第三个月植树400棵,设植树月平均增长率为x,
∴.
故选:B.
10.A
【分析】本题主要考查了一元二次方程根与系数的关系,根的判别式,先由根与系数的关系得到,,再由已知条件得到,解方程得到m的值,再利用判别式求解即可.
【详解】解:∵,是关于x的一元二次方程的两个实数根,
∴,,
∵,
∴,
∴,
解得或,
∵,
∴,
∴,
∴,
故选:A.
11.
【分析】本题考查了一元二次方程的根的判别式与根的关系,熟练掌握根的判别式与根的关系是解答本题的关键.当时,一元二次方程有两个不相等的实数根;当时,一元二次方程有两个相等的实数根;当时,一元二次方程没有实数根.根据根的判别式大于或等于零求解即可.
【详解】解:由题意得,,
.
故答案为:.
12.2
【分析】本题主要考查了一元二次方程根的判别式,对于一元二次方程,若,则方程有两个不相等的实数根,若,则方程有两个相等的实数根,若,则方程没有实数根,利用一元二次方程根的判别式求解即可.
【详解】解:∵一元二次方程有两个相等的实数根,
∴,
解得,
故答案为:2.
13.
【分析】此题考查了一元二次方程的应用,设年平均增长率是,根据题意列出方程即可,根据题意列出方程是解题的关键.
【详解】设年平均增长率是,
根据题意列方程:,
解得:(不合题意,舍去),,
故答案为:.
14.
【分析】本题考查了一元二次方程的解,解一元二次方程,根据题意得出,进而解方程,即可求解.
【详解】解:∵方程有一个解为,
∴
∴
即
∴
解得:
故答案为:.
15.2020
【分析】本题考查了一元二次方程的根,代数式求值,熟练掌握知识点是解题的关键.
由题意得,则,然后整体代入化简求值即可.
【详解】解:由题意得,
则,
∴,
∴
故答案为:2020.
16.
【分析】此题考查了一元二次方程的一般形式.注意一元二次方程的一般形式是:,,是常数且,其中,,分别叫二次项系数,一次项系数,常数项.首先将方程化为一般形式:,然后根据此一般形式,即可求得答案.
【详解】解:,
,
,
.
方程化成一般形式是,
常数项为.
故答案为:.
17.,
【分析】本题考查一元二次方程根与系数关系,能够根据根与系数的关系求得没有看错的未知字母的值是解题的关键.
首先根据根与系数的关系求得m,n的值,再进一步解方程即可.
【详解】解:根据根与系数关系得
,,
解得:,,
∴原方程为,
,
或,
∴,,
故答案为:,.
18.且
【分析】本题考查了根的判别式,一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.利用判别式的意义得到,然后解不等式即可.
【详解】解:∵关于x的一元二次方程有两个不相等的实数根,
∴,
解得:且,
故答案为:且.
19.5
【分析】本题考查了一元二次方程的根与系数的关系,解一元二次方程,由一元二次方程根与系数的关系得出,再利用因式分解法解一元二次方程,最后代入计算即可得出答案,熟练掌握一元二次方程根与系数的关系是解此题的关键.
【详解】解:、是一元二次方程的两个根,且,
,
原方程为,
解得:,,
,
故答案为:.
20.
【分析】本题考查由实际问题抽象出一元二次方程.根据增长率问题,一般增长后的量=增长前的量×(1+增长率),关系式为:一月份月营业额+二月份月营业额+三月份月营业额,把相关数值代入即可求解.
【详解】解:一月份的营业额为200万元,平均每月增长率为,
二月份的营业额为,
三月份的营业额为,
可列方程为,
故答案为:.
21.(1),
(2),
【分析】本题考查了解一元二次方程,选择合适的方法进行计算是解此题的关键.
(1)利用因式分解法解一元二次方程即可;
(2)利用因式分解法解一元二次方程即可.
【详解】(1)解:∵,
∴,
∴或,
解得:,;
(2)解:∵,
∴,
∴或,
解得:,.
22.(1);
(2).
【分析】本题考查了一元二次方程根与系数的关系,若,为方程的两个根,则,与系数的关系式:,.
(1)由根据系数的关系得,,结合求出,进而可求出;
(2)根据求解即可.
【详解】(1)解:由题意得,,.
解,得,
∴
∴.
(2)由(1)得方程为
把代入方程得
.
23.(1)见解析
(2)4
【分析】本题考查根的判别式,因式分解法解方程:
(1)求出判别式的符号,判断即可;
(2)因式分解法解方程,再根据其中一个根是另一个根的3倍,分两种情况进行讨论求解即可.
【详解】(1)解:证明:∵,
∴该方程总有两个实数根;
(2)∵,
∴,
∴或,
∴,
∵方程的根都是整数,且其中一个根是另一个根的3倍,
∴或,
解得或(舍去),
∴a的值为4.
24.(1)截成长度分别为和两段,所构菱形面积为;
(2)不能构成面积为的菱形,理由见解析.
【分析】本题考查了一元二次方程的应用,菱形的面积,根据等量关系列出方程是解题的关键.
(1)设其中一段的长为,则另一段的长为,依题意列出一元二次方程,求解即可;
(2)由(1)可得,,即,因为,方程无解,即可判断.
【详解】(1)解:将一根长为的小棒截成两段,设其中一段的长为,则另一段的长为,依题意得:
,
∴,
解得:,,
当时,,当时,,
∴将一根长为的小棒截成长度分别为和两段,所构菱形面积为;
(2)解:由(1)可得:,
∴,
∵,
∴方程无解,
∴不能构成面积为的菱形.
25.(1)前三个月生产量的平均增长率为
(2)应该再增加3条生产线
【分析】本题考查了一元二次方程的应用;
(1)设前三个月生产量的月增长率为x,根据题意列出一元二次方程,解方程,即可求解;
(2)设应该再增加m条生产线,则每条生产线的最大产能为万个/月,根据题意,列出一元二次方程,解方程,即可求解.
【详解】(1)解:设前三个月生产量的月增长率为x,
依题意得:,
解得:(不符合题意,舍去),
答:前三个月生产量的平均增长率为;
(2)设应该再增加m条生产线,则每条生产线的最大产能为万个/月,
依题意得:,
,
解得:,
又∵在增加产能同时又要节省投入成本,
.
答:应该再增加3条生产线.
26.(1)
(2)2
(3)1
(4)1
【分析】本题考查了一元二次方程的应用,矩形的性质等知识,解题的关键是:
(1)根据线段垂直平分线的性质得出,可列出关于t的方程,然后求解即可;
(2)根据勾股定理列方程求解即可;
(3)根据三角形面积公式列方程求解即可;
(4)根据的面积与五边形的面积之比等于,得出的面积与矩形的面积之比等于,然后根据三角形面积公式列方程求解即可.
【详解】(1)解∶∵点在的垂直平分线上,
∴,
∴,
解得,
∴当时,点在的垂直平分线上;
(2)解:∵的长度等于,,
∴,
∴,
解得,(舍去)
∴当时,的长度等于;
(3)解:∵的面积等于,
∴,
解得,(舍去)
∴当时,的面积等于,
(4)解:∵的面积与五边形的面积之比等于,
∴的面积与矩形的面积之比等于,
∴,
解得,(舍去)
∴当时,的面积与五边形的面积之比等于.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十一章一元二次方程综单元试题
一、单选题(每题3分,共30分)
1.下列方程中,是一元二次方程的是( )
A. B.
C. D.
2.若关于x的方程的一个根为3,则m的值为( )
A.3 B. C.4 D.
3.已知,是一元二次方程的两个根,则的值是( )
A.4 B. C. D.2
4.近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为21万元,5月份售价为18万元.设该款汽车这两月售价的月均下降率是x,则所列方程正确的是( )
A. B. C. D.
5.关于方程的根的说法中,正确的是( )
A.没有实数根 B.有两个不相等的实数根
C.两个实数根的和为2 D.两个实数根的积为-3
6.若关于x的一元二次方程两根为、,且,则p的值为( )
A. B. C. D.6
7.若一元二次方程的根判别式的值为,则的值为( )
A.1 B. C.3 D.
8.关于的一元二次方程的两个实数根分别为2和,则分解因式等于( )
A. B. C. D.
9.为推进节能减排,创建低碳绿色城市,学校计划植一批樟树,第一个月植树100棵,第三个月植树400棵,设植树月平均增长率为x,根据题意,请列出方程( )
A. B.
C. D.
10.设,是关于x的一元二次方程的两个实数根,且,则m的值为( )
A.2 B.4 C.2或 D.或4
二、填空题(每题3分,共30分)
11.关于的方程有实数根,则的取值范围为 .
12.已知关于x的一元二次方程有两个相等的实数根,则a的值为 .
13.某乡镇年旅游总收入为万元,到年旅游总收入达万元.若每年的平均增长率相同,则年平均增长率是 .
14.若方程有一个解为,则方程的解为 .
15.若m是方程的一个实数根,则代数式的值为 .
16.方程的一次项系数是,二次项系数是 2,常数项是 .
17.在解方程时,小王看错了m,解得方程的根为6与;小李看错了n,解得方程的根为2与,则原方程的解为 .
18.已知关于x的一元二次方程有两个不相等的实数根,则实数k的取值范围是 .
19.设、是一元二次方程的两个根,且,则 .
20.某超市一月份的营业额为200万元,第一季度总营业额为800万元,设平均每月营业额的增长率为x,则由题意列方程为 .
三、解答题(共60分)
21.解方程:
(1); (2).
22.已知:,是关于的一元二次方程的两个根.
(1)若,求的值;
(2)在(1)的条件下,求的值.
23.已知关于x的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若该方程的两个实数根都是整数,且其中一个根是另一个根的3倍,求a的值.
24.在课外活动中,小华根据学习平行四边形、菱形、正方形的经验对其面积进行了研究.他将一根长为的小棒截成两段,并将之放置在互相垂直平分的位置上,将端点用橡皮筋连接,即构造出了菱形.
(1)若所构菱形面积为,则应如何截取?
(2)所构菱形面积可以为吗?试说明理由.
25.某芯片公司引进了一条内存芯片生产线,开工第一个月生产80万个,第三个月生产96.8万个.
(1)已知每个月生产量的增长率相等,求前三个月生产量的月增长率;
(2)经调查发现,1条生产线最大产能是150万个/月,若每增加1条生产线,每条生产线的最大产能将减少6万个/月,现该公司要保证每月生产内存芯片528万个,在增加产能同时又要节省投入成本的条件下(生产线越多,投入成本越大),应该再增加几条生产线?
26.如图,在矩形中,,点从点开始沿边向终点以的速度移动,与此同时,点Q从点B开始沿边向终点C以的速度移动.如果分别从同时出发,当点运动到点时;两点停止运动,设运动时间为秒.
(1)当为何值时,点在的垂直平分线上?
(2)当为何值时,的长度等于?
(3)连接,是否存在的值,使得的面积等于?若存在,请求出此时的值;若不存在,请说明理由.
(4)是否存在的值,使得的面积与五边形的面积之比等于?若存在,请求出此时的值;若不存在,请说明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】本题主要考查了一元二次方程的定义,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
根据一元二次方程的定义逐个分析即可解答:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
【详解】解:A、中含有两个未知数,故不是一元二次方程,不合题意;
B、是分式方程,不符合题意;
C、是无理方程,故不是一元二次方程,不合题意;
D、是一元二次方程,符合题意.
故选:B.
2.C
【分析】本题主要考查了一元二次方程的解,将代入,解关于m的方程即可.
【详解】解:将代入,得:,
解得,
故选C.
3.D
【分析】本题考查了一元二次方程的根与系数关系,根据根与系数关系可得,,代入即可解答.
【详解】解:∵是一元二次方程,即的两个实数根,
∴,,
∴.
故选:D
4.D
【分析】此题主要考查了一元二次方程的应用.首先根据3月份售价为21万元,月均下降率是可得出4月份的售价为万元,5月份的售价为万元,据此根据5月份售价为18万元可列出方程,进而可得出答案.
【详解】解:月份售价为21万元,月均下降率是,5月份售价为18万元,
.
故选:D.
5.B
【分析】此题考查了一元二次方程根的判别式,先求出一元二次方程根的判别式的值,再根据判别式的值即可得到答案.
【详解】解:对于方程,
∵,
∴,
∴方程有两个不相等的实数根,
故选:B
6.A
【分析】本题考查了一元二次方程根与系数的关系:若方程的两实数根为,则.
根据一元二次方程根与系数的关系得到,然后通分,,从而得到关于p的方程,解方程即可.
【详解】解:,
,
而,
,
,
故选:A.
7.B
【分析】本题考查了一元二次方程根的判别式;利用一元二次方程根的判别式即可解决问题.
【详解】解:因为一元二次方程的根判别式的值为,
所以,
解得.
故选:B.
8.C
【分析】本题考查了一元二次方程根的性质,由题意得出方程可以化为,即可得出答案.
【详解】解:∵关于的一元二次方程的两个实数根分别为2和,
∴方程可以化为,
∴,
故选:C.
9.B
【分析】利用第三个月该植树棵数第一个月该校植树棵数该校植树棵数的年平均增长率),即可列出关于的一元二次方程,此题得解.本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
【详解】解:∵第一个月植树100棵,第三个月植树400棵,设植树月平均增长率为x,
∴.
故选:B.
10.A
【分析】本题主要考查了一元二次方程根与系数的关系,根的判别式,先由根与系数的关系得到,,再由已知条件得到,解方程得到m的值,再利用判别式求解即可.
【详解】解:∵,是关于x的一元二次方程的两个实数根,
∴,,
∵,
∴,
∴,
解得或,
∵,
∴,
∴,
∴,
故选:A.
11.
【分析】本题考查了一元二次方程的根的判别式与根的关系,熟练掌握根的判别式与根的关系是解答本题的关键.当时,一元二次方程有两个不相等的实数根;当时,一元二次方程有两个相等的实数根;当时,一元二次方程没有实数根.根据根的判别式大于或等于零求解即可.
【详解】解:由题意得,,
.
故答案为:.
12.2
【分析】本题主要考查了一元二次方程根的判别式,对于一元二次方程,若,则方程有两个不相等的实数根,若,则方程有两个相等的实数根,若,则方程没有实数根,利用一元二次方程根的判别式求解即可.
【详解】解:∵一元二次方程有两个相等的实数根,
∴,
解得,
故答案为:2.
13.
【分析】此题考查了一元二次方程的应用,设年平均增长率是,根据题意列出方程即可,根据题意列出方程是解题的关键.
【详解】设年平均增长率是,
根据题意列方程:,
解得:(不合题意,舍去),,
故答案为:.
14.
【分析】本题考查了一元二次方程的解,解一元二次方程,根据题意得出,进而解方程,即可求解.
【详解】解:∵方程有一个解为,
∴
∴
即
∴
解得:
故答案为:.
15.2020
【分析】本题考查了一元二次方程的根,代数式求值,熟练掌握知识点是解题的关键.
由题意得,则,然后整体代入化简求值即可.
【详解】解:由题意得,
则,
∴,
∴
故答案为:2020.
16.
【分析】此题考查了一元二次方程的一般形式.注意一元二次方程的一般形式是:,,是常数且,其中,,分别叫二次项系数,一次项系数,常数项.首先将方程化为一般形式:,然后根据此一般形式,即可求得答案.
【详解】解:,
,
,
.
方程化成一般形式是,
常数项为.
故答案为:.
17.,
【分析】本题考查一元二次方程根与系数关系,能够根据根与系数的关系求得没有看错的未知字母的值是解题的关键.
首先根据根与系数的关系求得m,n的值,再进一步解方程即可.
【详解】解:根据根与系数关系得
,,
解得:,,
∴原方程为,
,
或,
∴,,
故答案为:,.
18.且
【分析】本题考查了根的判别式,一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.利用判别式的意义得到,然后解不等式即可.
【详解】解:∵关于x的一元二次方程有两个不相等的实数根,
∴,
解得:且,
故答案为:且.
19.5
【分析】本题考查了一元二次方程的根与系数的关系,解一元二次方程,由一元二次方程根与系数的关系得出,再利用因式分解法解一元二次方程,最后代入计算即可得出答案,熟练掌握一元二次方程根与系数的关系是解此题的关键.
【详解】解:、是一元二次方程的两个根,且,
,
原方程为,
解得:,,
,
故答案为:.
20.
【分析】本题考查由实际问题抽象出一元二次方程.根据增长率问题,一般增长后的量=增长前的量×(1+增长率),关系式为:一月份月营业额+二月份月营业额+三月份月营业额,把相关数值代入即可求解.
【详解】解:一月份的营业额为200万元,平均每月增长率为,
二月份的营业额为,
三月份的营业额为,
可列方程为,
故答案为:.
21.(1),
(2),
【分析】本题考查了解一元二次方程,选择合适的方法进行计算是解此题的关键.
(1)利用因式分解法解一元二次方程即可;
(2)利用因式分解法解一元二次方程即可.
【详解】(1)解:∵,
∴,
∴或,
解得:,;
(2)解:∵,
∴,
∴或,
解得:,.
22.(1);
(2).
【分析】本题考查了一元二次方程根与系数的关系,若,为方程的两个根,则,与系数的关系式:,.
(1)由根据系数的关系得,,结合求出,进而可求出;
(2)根据求解即可.
【详解】(1)解:由题意得,,.
解,得,
∴
∴.
(2)由(1)得方程为
把代入方程得
.
23.(1)见解析
(2)4
【分析】本题考查根的判别式,因式分解法解方程:
(1)求出判别式的符号,判断即可;
(2)因式分解法解方程,再根据其中一个根是另一个根的3倍,分两种情况进行讨论求解即可.
【详解】(1)解:证明:∵,
∴该方程总有两个实数根;
(2)∵,
∴,
∴或,
∴,
∵方程的根都是整数,且其中一个根是另一个根的3倍,
∴或,
解得或(舍去),
∴a的值为4.
24.(1)截成长度分别为和两段,所构菱形面积为;
(2)不能构成面积为的菱形,理由见解析.
【分析】本题考查了一元二次方程的应用,菱形的面积,根据等量关系列出方程是解题的关键.
(1)设其中一段的长为,则另一段的长为,依题意列出一元二次方程,求解即可;
(2)由(1)可得,,即,因为,方程无解,即可判断.
【详解】(1)解:将一根长为的小棒截成两段,设其中一段的长为,则另一段的长为,依题意得:
,
∴,
解得:,,
当时,,当时,,
∴将一根长为的小棒截成长度分别为和两段,所构菱形面积为;
(2)解:由(1)可得:,
∴,
∵,
∴方程无解,
∴不能构成面积为的菱形.
25.(1)前三个月生产量的平均增长率为
(2)应该再增加3条生产线
【分析】本题考查了一元二次方程的应用;
(1)设前三个月生产量的月增长率为x,根据题意列出一元二次方程,解方程,即可求解;
(2)设应该再增加m条生产线,则每条生产线的最大产能为万个/月,根据题意,列出一元二次方程,解方程,即可求解.
【详解】(1)解:设前三个月生产量的月增长率为x,
依题意得:,
解得:(不符合题意,舍去),
答:前三个月生产量的平均增长率为;
(2)设应该再增加m条生产线,则每条生产线的最大产能为万个/月,
依题意得:,
,
解得:,
又∵在增加产能同时又要节省投入成本,
.
答:应该再增加3条生产线.
26.(1)
(2)2
(3)1
(4)1
【分析】本题考查了一元二次方程的应用,矩形的性质等知识,解题的关键是:
(1)根据线段垂直平分线的性质得出,可列出关于t的方程,然后求解即可;
(2)根据勾股定理列方程求解即可;
(3)根据三角形面积公式列方程求解即可;
(4)根据的面积与五边形的面积之比等于,得出的面积与矩形的面积之比等于,然后根据三角形面积公式列方程求解即可.
【详解】(1)解∶∵点在的垂直平分线上,
∴,
∴,
解得,
∴当时,点在的垂直平分线上;
(2)解:∵的长度等于,,
∴,
∴,
解得,(舍去)
∴当时,的长度等于;
(3)解:∵的面积等于,
∴,
解得,(舍去)
∴当时,的面积等于,
(4)解:∵的面积与五边形的面积之比等于,
∴的面积与矩形的面积之比等于,
∴,
解得,(舍去)
∴当时,的面积与五边形的面积之比等于.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
