第六章 立体几何初步 A卷基础夯实(含解析)——2024-2025学年高一数学北师大2019必修第二册单元达标测试卷
文档属性
| 名称 | 第六章 立体几何初步 A卷基础夯实(含解析)——2024-2025学年高一数学北师大2019必修第二册单元达标测试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 18:08:49 | ||
图片预览




文档简介
第六章 立体几何初步 A卷 基础夯实——2024-2025学年高一数学北师大2019必修第二册单元达标测试卷
一、选择题
1.若棱台的上、下底面面积分别为4,16,高为3,则该棱台的体积为( )
A.26 B.28 C.30 D.32
2.已知三棱锥的所有顶点都在球O的球面上,是边长为1的正三角形,SC为球O的直径,且,则此棱锥的体积为( )
A. B. C. D.
3.已知两条不同的直线m,n和平面,且,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.《九章算术》涉及算术、代数、几何等诸多领域,书中有如下问题:“今有圆亭,下周三丈,上周二丈,高二丈,问积几何?”其意思为:“有一个圆台,下底周长为3丈,上底周长为2丈,高为2丈,那么该圆台的体积是多少?”已知1丈等于10尺,圆周率约为3,估算出这个圆台体积约有( )
A.立方尺 B.立方尺 C.立方尺 D.立方尺
5.如图1,球面被平面截得的一部分叫做球冠,截得的圆面是底,圆的半径记为R,垂直于截面的直径被截得的一段叫做球冠的高,记为H,则球冠的曲面面积.球O是棱长为1的正方体的棱切球,则球O在正方体外面部分曲面的面积为( )
A. B. C. D.
6.已知某圆台的上底面和下底面的面积分别为、,高为6,则该圆台的体积为( )
A. B. C. D.
7.用斜二测画法得到一个水平放置的四边形的直观图为如图所示的直角梯形,已知,,,四边形的面积为,则( )
A.1 B. C. D.
8.已知两条不同的直线a,b及两个不同的平面,,则下列说法正确的是( )
A.若,,,则
B.若,,,则a与b是异面直线
C.若,,,则a与b平行或异面
D.若,,则a与一定相交
二、多项选择题
9.如图,在四棱锥中,底面ABCD为菱形,,侧面PAD为正三角形,且平面平面ABCD,则下列说法正确的有( )
A.在线段AD上存在一点M,使平面PMB
B.异面直线AD与PB所成的角为
C.二面角的大小为
D.平面PAC
10.下列说法中不正确的是( )
A.棱柱的侧面可以是三角形 B.正方体和长方体都是特殊的四棱柱
C.所有几何体的表面都能展开成平面图形 D.棱柱的各条棱都相等
11.在正方体的8个顶点中任意取4个不同的顶点,则这4个顶点可能构成( )
A.矩形
B.每个面都是等边三角形的四面体
C.每个面都是直角三角形的四面体
D.有三个面是直角三角形、一个面是等边三角形的四面体
三、填空题
12.底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为____________.
13.已知水平放置的四边形ABCD的斜二测直观图为矩形,已知,,则四边形ABCD的面积为________.
14.水平放置的的直观图如图所示,已知,,则AB边上的中线的实际长度为________.
四、解答题
15.如图,在三棱锥中,平面平面,,O为BD的中点.
(1)证明:;
(2)若是边长为1的等边三角形,点E在棱AD上,,且二面角的大小为,求三棱锥的体积.
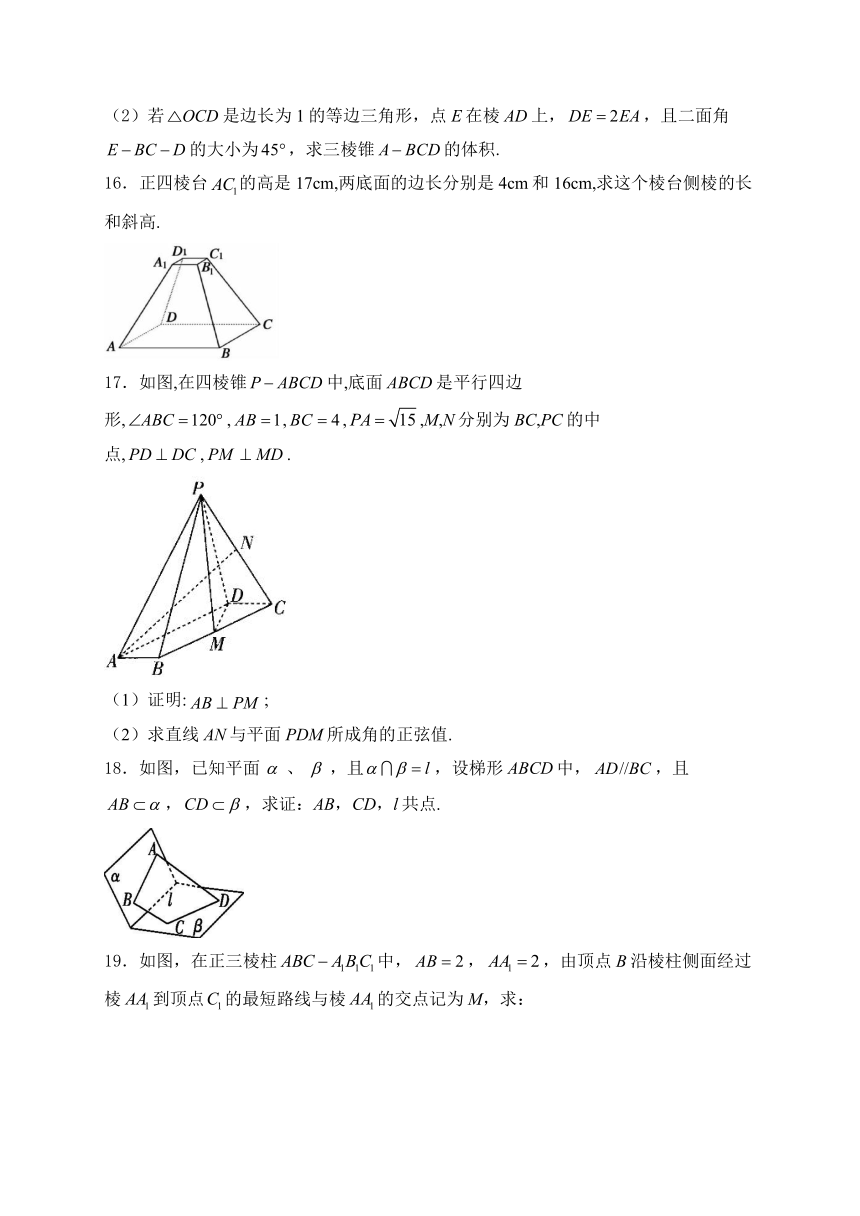
16.正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高.
17.如图,在四棱锥中,底面ABCD是平行四边形,,,,,M,N分别为BC,PC的中点,,.
(1)证明:;
(2)求直线AN与平面PDM所成角的正弦值.
18.如图,已知平面、,且,设梯形ABCD中,,且,,求证:AB,CD,l共点.
19.如图,在正三棱柱中,,,由顶点B沿棱柱侧面经过棱到顶点的最短路线与棱的交点记为M,求:
(1)三棱柱的侧面展开图的对角线长;
(2)该最短路线的长及的值;
(3)平面与平面ABC所成二面角(锐角)的大小.
参考答案
1.答案:B
解析:所求棱台的体积为
故选:B.
2.答案:A
解析:在中,,,,所以;同理,,过A点作SC的垂线交SC于D点,连接DB,因为,故,故平面ABD,且为等腰三角形.因为,故,则的面积为,则三棱锥的体积为.
3.答案:D
解析:如图,取平面为平面,直线为n,
不妨取直线为m,显然有,此时,即推不出,
不妨取直线为直线m,显然有,此时,即推不出,
故选:D.
4.答案:D
解析:如图所示,
设圆台上底半径为,下底半径为,则,,
解得:,,
即:下底半径为5尺,上底半径为尺,
设,分别为上下底面面积,
所以圆台的体积为:立方尺.
故选:D.
5.答案:D
解析:如图1,正方体与正方体的棱切球形成六个球冠,且,,所以所求曲面的面积为:,故选D,
6.答案:C
解析:该圆台的体积为.
7.答案:D
解析:如图所示,根据斜二测画法的规则,得到原四边形
,设,则,则,
,且为原图形中梯形的高,
故,解得,故,
故选:D.
8.答案:C
解析:若,,,则直线a,b没有交点,故a与b平行或异面,故A,B错误,C正确;若,,当时,a与平行,故D错误.故选C.
9.答案:ABC
解析:对于A选项,如图,取AD的中点M,连接PM,BM,
设AC与BD交于点O.侧面PAD为正三角形,.又底面ABCD是菱形,,是等边三角形,.又,平面,平面PMB,故A正确.
对于B选项,平面,平面,,即异面直线AD与PB所成的角为,故B正确.
对于C选项,,平面.平面,,.又平面平面,是二面角的平面角.设,则,.在中,,即,故二面角的大小为,故C正确.
对于D选项,易得,与PA不垂直,与平面PAC不垂直,故D错误.故选ABC.
10.答案:ACD
解析:棱柱的侧面都是四边形,A不正确;正方体和长方体都是特殊的四棱柱,B正确;不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;棱柱的各条棱并不是都相等,应该为棱柱的侧棱都相等,D不正确.故选ACD.
11.答案:ABCD
解析:对于A,如图四边形为矩形,所以A正确,
对于B,四面体的每个面都是等边三角形,所以B正确,
对于C,如图四面体的每个面都是直角三角形,所以C正确,
对于D,如图四面体的三个面是直角三角形、一个面是等边三角形,所以D正确,
故选:ABCD.
12.答案:28
解析:方法一:由于,而截去的正四棱锥的高为3,所以原正四棱锥的高为6,所以原正四棱锥的体积为,截去的正四棱锥的体积为,所以棱台的体积为.
方法二:由方法一可知,棱台的体积为.故答案为28.
13.答案:
解析:
14.答案:
解析:根据斜二测画法的原则,由直观图知,原平面图形为直角三角形,
且,,,
所以,
所以,
故AB边上中线长为.
故答案为:.
15、
(1)答案:证明见解析
解析:因为,O为BD的中点,
所以,
又平面平面BCD,且平面平面,平面ABD,所以平面BCD,
又平面BCD,所以.
(2)答案:
解析:因为是边长为1的正三角形,且O为BD的中点,
所以,
所以是直角三角形,且,,所以.
如图,过点E作,交BD于F,过点F作,垂足为G,连接EG.
因为平面BCD,
所以平面BCD.
又平面BCD,所以.
又,且,平面EFG,
所以平面EFG,
则为二面角的平面角,
所以,则.
因为,所以,,所以.
因为,,所以,
则,所以.
所以,所以,
所以.
16.答案:棱台的侧棱长为19cm,斜高为
解析:如图所示,设棱台的两底面的中心分别是和O,和BC的中点分别是和E,连接,,,OB,,OE,则四边形和都是直角梯形.
,,
,,,.
,
.
,.
即棱台的侧棱长为19cm,斜高为.
17.答案:证明见解析;
(2)
解析:(1)由题意知,,,
易得.
又,且,平面PDM,
所以平面PDM.
因为,所以平面PDM.
又平面PDM,所以.
(2)由(1)知平面PDM,所以为直线AN与平面PDM所成角的余角.
连接AM,因为,,
所以平面ABCD,所以.
因为,,,
所以由余弦定理得,
又,所以,
所以,
连接BN,结合余弦定理得.
连接AC,则由余弦定理得,
在中,结合余弦定理得,所以.
所以在中,.
设直线AN与平面PDM所成的角为,
则.
18.答案:证明见解析
解析:证明如图,在梯形ABCD中,,
与CD所在的直线必交于一点,设两直线交于点M,则直线AB,直线CD.
,,,,
又,,直线AB,CD,l共点.
19.答案:(1)
(2)最短路线的长为,此时
(3)
解析:(1)正三棱柱的侧面展开图是长为6,宽为2的矩形,
其对角线长为.
(2)如图,将侧面绕棱顺时针旋转使其与侧面在同一平面上,点B旋转到点D的位置.
连接交于点M,则是由顶点B沿棱柱侧面经过棱到顶点的最短路线,
.
,,,
,,故.
即最短路线的长为,此时.
(3)如图,连接DB,则DB是平面与平面ABC的交线.
在中,,.
又平面平面ABC,平面平面,平面,平面,
,是平面与平面ABC所成二面角的平面角(锐角).
侧面是正方形,.
故平面与平面ABC所成的二面角(锐角)的大小为.
一、选择题
1.若棱台的上、下底面面积分别为4,16,高为3,则该棱台的体积为( )
A.26 B.28 C.30 D.32
2.已知三棱锥的所有顶点都在球O的球面上,是边长为1的正三角形,SC为球O的直径,且,则此棱锥的体积为( )
A. B. C. D.
3.已知两条不同的直线m,n和平面,且,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.《九章算术》涉及算术、代数、几何等诸多领域,书中有如下问题:“今有圆亭,下周三丈,上周二丈,高二丈,问积几何?”其意思为:“有一个圆台,下底周长为3丈,上底周长为2丈,高为2丈,那么该圆台的体积是多少?”已知1丈等于10尺,圆周率约为3,估算出这个圆台体积约有( )
A.立方尺 B.立方尺 C.立方尺 D.立方尺
5.如图1,球面被平面截得的一部分叫做球冠,截得的圆面是底,圆的半径记为R,垂直于截面的直径被截得的一段叫做球冠的高,记为H,则球冠的曲面面积.球O是棱长为1的正方体的棱切球,则球O在正方体外面部分曲面的面积为( )
A. B. C. D.
6.已知某圆台的上底面和下底面的面积分别为、,高为6,则该圆台的体积为( )
A. B. C. D.
7.用斜二测画法得到一个水平放置的四边形的直观图为如图所示的直角梯形,已知,,,四边形的面积为,则( )
A.1 B. C. D.
8.已知两条不同的直线a,b及两个不同的平面,,则下列说法正确的是( )
A.若,,,则
B.若,,,则a与b是异面直线
C.若,,,则a与b平行或异面
D.若,,则a与一定相交
二、多项选择题
9.如图,在四棱锥中,底面ABCD为菱形,,侧面PAD为正三角形,且平面平面ABCD,则下列说法正确的有( )
A.在线段AD上存在一点M,使平面PMB
B.异面直线AD与PB所成的角为
C.二面角的大小为
D.平面PAC
10.下列说法中不正确的是( )
A.棱柱的侧面可以是三角形 B.正方体和长方体都是特殊的四棱柱
C.所有几何体的表面都能展开成平面图形 D.棱柱的各条棱都相等
11.在正方体的8个顶点中任意取4个不同的顶点,则这4个顶点可能构成( )
A.矩形
B.每个面都是等边三角形的四面体
C.每个面都是直角三角形的四面体
D.有三个面是直角三角形、一个面是等边三角形的四面体
三、填空题
12.底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为____________.
13.已知水平放置的四边形ABCD的斜二测直观图为矩形,已知,,则四边形ABCD的面积为________.
14.水平放置的的直观图如图所示,已知,,则AB边上的中线的实际长度为________.
四、解答题
15.如图,在三棱锥中,平面平面,,O为BD的中点.
(1)证明:;
(2)若是边长为1的等边三角形,点E在棱AD上,,且二面角的大小为,求三棱锥的体积.
16.正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高.
17.如图,在四棱锥中,底面ABCD是平行四边形,,,,,M,N分别为BC,PC的中点,,.
(1)证明:;
(2)求直线AN与平面PDM所成角的正弦值.
18.如图,已知平面、,且,设梯形ABCD中,,且,,求证:AB,CD,l共点.
19.如图,在正三棱柱中,,,由顶点B沿棱柱侧面经过棱到顶点的最短路线与棱的交点记为M,求:
(1)三棱柱的侧面展开图的对角线长;
(2)该最短路线的长及的值;
(3)平面与平面ABC所成二面角(锐角)的大小.
参考答案
1.答案:B
解析:所求棱台的体积为
故选:B.
2.答案:A
解析:在中,,,,所以;同理,,过A点作SC的垂线交SC于D点,连接DB,因为,故,故平面ABD,且为等腰三角形.因为,故,则的面积为,则三棱锥的体积为.
3.答案:D
解析:如图,取平面为平面,直线为n,
不妨取直线为m,显然有,此时,即推不出,
不妨取直线为直线m,显然有,此时,即推不出,
故选:D.
4.答案:D
解析:如图所示,
设圆台上底半径为,下底半径为,则,,
解得:,,
即:下底半径为5尺,上底半径为尺,
设,分别为上下底面面积,
所以圆台的体积为:立方尺.
故选:D.
5.答案:D
解析:如图1,正方体与正方体的棱切球形成六个球冠,且,,所以所求曲面的面积为:,故选D,
6.答案:C
解析:该圆台的体积为.
7.答案:D
解析:如图所示,根据斜二测画法的规则,得到原四边形
,设,则,则,
,且为原图形中梯形的高,
故,解得,故,
故选:D.
8.答案:C
解析:若,,,则直线a,b没有交点,故a与b平行或异面,故A,B错误,C正确;若,,当时,a与平行,故D错误.故选C.
9.答案:ABC
解析:对于A选项,如图,取AD的中点M,连接PM,BM,
设AC与BD交于点O.侧面PAD为正三角形,.又底面ABCD是菱形,,是等边三角形,.又,平面,平面PMB,故A正确.
对于B选项,平面,平面,,即异面直线AD与PB所成的角为,故B正确.
对于C选项,,平面.平面,,.又平面平面,是二面角的平面角.设,则,.在中,,即,故二面角的大小为,故C正确.
对于D选项,易得,与PA不垂直,与平面PAC不垂直,故D错误.故选ABC.
10.答案:ACD
解析:棱柱的侧面都是四边形,A不正确;正方体和长方体都是特殊的四棱柱,B正确;不是所有几何体的表面都能展开成平面图形,球不能展开成平面图形,C不正确;棱柱的各条棱并不是都相等,应该为棱柱的侧棱都相等,D不正确.故选ACD.
11.答案:ABCD
解析:对于A,如图四边形为矩形,所以A正确,
对于B,四面体的每个面都是等边三角形,所以B正确,
对于C,如图四面体的每个面都是直角三角形,所以C正确,
对于D,如图四面体的三个面是直角三角形、一个面是等边三角形,所以D正确,
故选:ABCD.
12.答案:28
解析:方法一:由于,而截去的正四棱锥的高为3,所以原正四棱锥的高为6,所以原正四棱锥的体积为,截去的正四棱锥的体积为,所以棱台的体积为.
方法二:由方法一可知,棱台的体积为.故答案为28.
13.答案:
解析:
14.答案:
解析:根据斜二测画法的原则,由直观图知,原平面图形为直角三角形,
且,,,
所以,
所以,
故AB边上中线长为.
故答案为:.
15、
(1)答案:证明见解析
解析:因为,O为BD的中点,
所以,
又平面平面BCD,且平面平面,平面ABD,所以平面BCD,
又平面BCD,所以.
(2)答案:
解析:因为是边长为1的正三角形,且O为BD的中点,
所以,
所以是直角三角形,且,,所以.
如图,过点E作,交BD于F,过点F作,垂足为G,连接EG.
因为平面BCD,
所以平面BCD.
又平面BCD,所以.
又,且,平面EFG,
所以平面EFG,
则为二面角的平面角,
所以,则.
因为,所以,,所以.
因为,,所以,
则,所以.
所以,所以,
所以.
16.答案:棱台的侧棱长为19cm,斜高为
解析:如图所示,设棱台的两底面的中心分别是和O,和BC的中点分别是和E,连接,,,OB,,OE,则四边形和都是直角梯形.
,,
,,,.
,
.
,.
即棱台的侧棱长为19cm,斜高为.
17.答案:证明见解析;
(2)
解析:(1)由题意知,,,
易得.
又,且,平面PDM,
所以平面PDM.
因为,所以平面PDM.
又平面PDM,所以.
(2)由(1)知平面PDM,所以为直线AN与平面PDM所成角的余角.
连接AM,因为,,
所以平面ABCD,所以.
因为,,,
所以由余弦定理得,
又,所以,
所以,
连接BN,结合余弦定理得.
连接AC,则由余弦定理得,
在中,结合余弦定理得,所以.
所以在中,.
设直线AN与平面PDM所成的角为,
则.
18.答案:证明见解析
解析:证明如图,在梯形ABCD中,,
与CD所在的直线必交于一点,设两直线交于点M,则直线AB,直线CD.
,,,,
又,,直线AB,CD,l共点.
19.答案:(1)
(2)最短路线的长为,此时
(3)
解析:(1)正三棱柱的侧面展开图是长为6,宽为2的矩形,
其对角线长为.
(2)如图,将侧面绕棱顺时针旋转使其与侧面在同一平面上,点B旋转到点D的位置.
连接交于点M,则是由顶点B沿棱柱侧面经过棱到顶点的最短路线,
.
,,,
,,故.
即最短路线的长为,此时.
(3)如图,连接DB,则DB是平面与平面ABC的交线.
在中,,.
又平面平面ABC,平面平面,平面,平面,
,是平面与平面ABC所成二面角的平面角(锐角).
侧面是正方形,.
故平面与平面ABC所成的二面角(锐角)的大小为.
同课章节目录
