六 比例尺 单元检测 (含解析)冀教版六年级上册
文档属性
| 名称 | 六 比例尺 单元检测 (含解析)冀教版六年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 170.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 19:05:55 | ||
图片预览




文档简介
六 比例尺——六年级数学冀教版上册同步单元小练习
一、选择题
1.一个长150米,宽90米的长方形广场,画在比例尺1∶3000的图纸上,长应画( )厘米。
A.3 B.5 C.15
2.一幅图的比例尺是60∶1,它表示图上长度是实际长度的( )。
A.160 B.61倍 C.60倍 D.59倍
3.在一张图纸上,用1厘米的线段表示2毫米的实际距离,这张图纸的比例尺是( )。
A. B. C. D.
4.学校操场的长是40米,按照1∶10000的比例尺把它画在图上应画( )。
A.4分米 B.4厘米 C.4毫米
5.郑开马拉松全程约为42千米,已知地图上量得郑开马拉松全程距离为2.1厘米,这张地图的比例尺为( )
A.1:20000 B.1:200000 C.1:2000000 D.1:20000000
二、填空题
6.2021年是中国共产党成立100周年,小明打算国庆节和父母一起到北京。他在一幅比例尺为1∶20000000的地图上量得成都到北京的距离约为9厘米,成都到北京的实际距离大约是( )千米。
7.比例尺1∶2000表示的含义是图上1( )表示实际距离( )米。
8.如图,书店在学校的( )偏( )方向( ),( )千米处。
9.一幅地图,用图上的4厘米表示实际的120米,这幅地图的比例尺是( )。
10.把改写成数值比例尺是( )。
三、判断题
11.一幅地图的比例尺可以是数值比例尺,也可以是线段比例尺。( )
12.比例尺就是图上距离与实际距离的比值。( )
13.把一个面积为100平方厘米的正方形按1∶10的比例尺画在平面图上,图上的面积是10平方厘米。( )
14.大林画出的示意图比原来图形大,大林使用的比例尺可能是1∶10。( )
15.一幅平面图的比例尺是1∶200,那么图上的正方形的面积与实际正方形面积的比是1∶200。( )
四、计算题
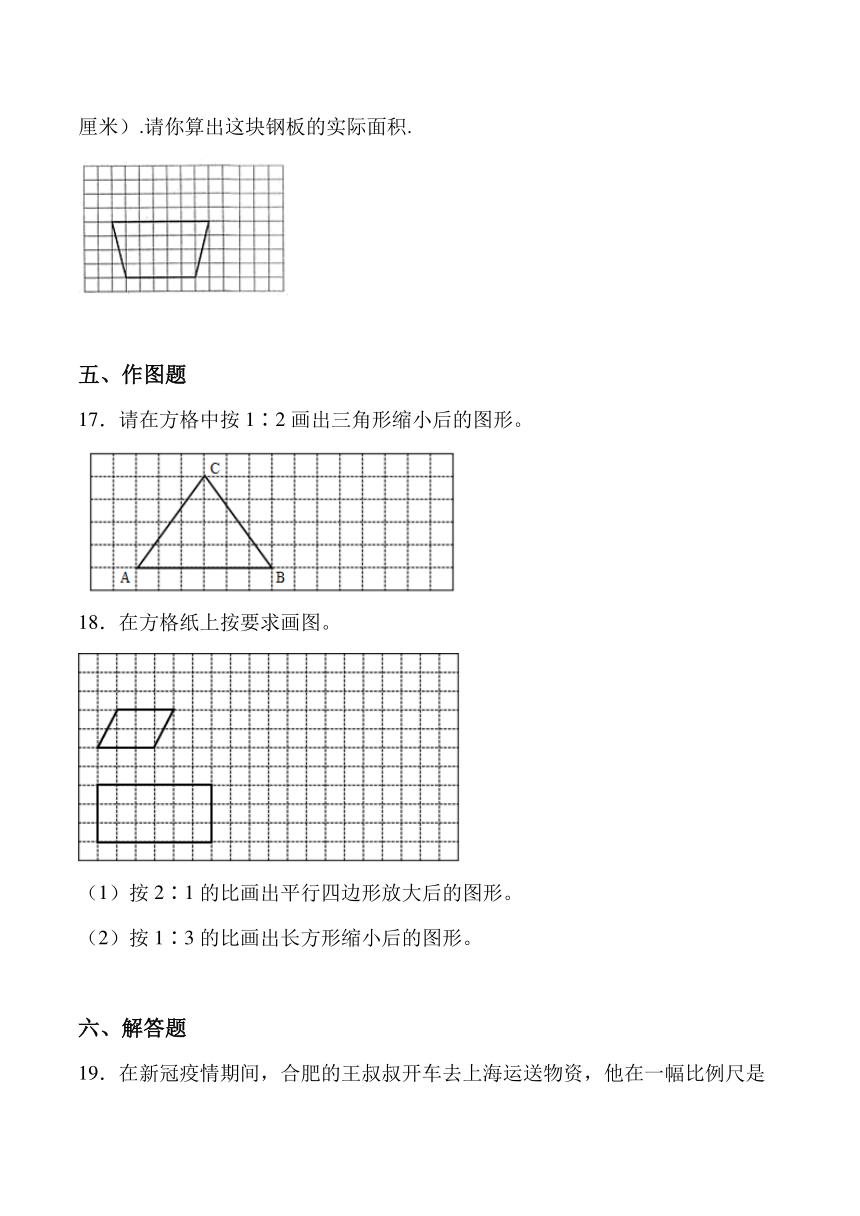
16.如图是一块钢板按1:100缩小后画在方格纸上的图形(每小格的边长是1厘米).请你算出这块钢板的实际面积.
五、作图题
17.请在方格中按1∶2画出三角形缩小后的图形。
18.在方格纸上按要求画图。
(1)按2∶1的比画出平行四边形放大后的图形。
(2)按1∶3的比画出长方形缩小后的图形。
六、解答题
19.在新冠疫情期间,合肥的王叔叔开车去上海运送物资,他在一幅比例尺是1∶4800000的地图上,量得合肥到上海的距离大约是10厘米,王叔叔开车以每小时96千米的速度行驶,几小时到达?
20.在比例尺是1∶2500000的地图上,量得A、B两地相距12厘米。如果李叔叔和王叔叔开车同时从两地相对出发,李叔叔开车每小时行105千米,王叔叔开车每小时行95千米。几小时后两人能相遇?
21.在一幅比例尺是1∶4500000的地图上量得甲地到乙地的距离是4厘米,爸爸开车从甲地出发,沿图上的路线到乙地用了2.5小时,平均每小时行驶多少千米?
答案以及解析
1.B
【解析】由比例尺=图上距离÷实际距离可知,图上距离=实际距离×比例尺,代入数据即可解答。
150米=15000厘米
15000×=5(厘米)
即长应画5厘米。
故答案为:B
明确实际距离、图上距离和比例尺之间的关系是解答本题的关键。
2.C
【解析】因为比例尺是图上距离与实际距离的比,比例尺60∶1是一个扩大的比例尺,即图上的60cm相当于实际的1cm,所以图上距离是实际距离的60倍。
60∶1
=60÷1
=60
它表示图上长度是实际长度的60倍。
故答案为:C
此题主要考查比例尺的意义:比例尺是图上距离与实际距离的比。
3.A
【解析】按照比例尺的定义,化简图上距离1厘米与实际距离2毫米的比即可。
1厘米=10毫米
10毫米∶2毫米
=5∶1
这张图纸的比例尺是5∶1。
故答案为:A。
本题的解题关键是掌握比例尺的定义,注意换算统一单位。
4.C
【解析】根据图上距离=实际距离×比例尺,求出图上的长即可。
40米=4000厘米
4000×=0.4(厘米)=4(毫米)
故答案为:C
此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题。
5.C
【解析】试题分析:根据比例尺=图上距离:实际距离,可直接求得这张地图的比例尺.
解答:解:42千米=4200000厘米,
比例尺=2.1:4200000=1:2000000.
答:这张地图的比例尺为1:2000000.
故选C.
考查了比例尺的意义,表示比例尺的时候,注意统一单位长度.
6.1800
【解析】根据图上距离÷比例尺=实际距离,用9÷即可求出9厘米的实际距离,再把单位换算成千米。
9÷
=9×20000000
=180000000(厘米)
180000000厘米=1800千米
成都到北京的实际距离大约是1800千米。
7. 厘米 20
【解析】根据比例尺的定义,图上距离是实际距离的,据此解答即可。
因为比例尺是1∶2000,所以图上距离1厘米表示实际距离2000厘米,2000厘米=20米。
由此可得:比例尺1∶2000表示的含义是图上1厘米表示实际距离20米。
此题主要考查比例尺的意义,解答时要注意单位的换算。
8. 西 北 30° 1.8
【解析】根据图上确定方向的方法:上北下南、左西右东,以学校为观测点,确定书店的方向,然后根据图上1厘米表示实际900米,求出2厘米的实际距离,据此解答。
2×900=1800(米)
1800米=1.8千米
书店在学校的西偏北方向30°,1.8千米处。
此题主要考查依据方向(角度)和距离确定物体位置的方法。
9.1∶3000
【解析】根据比例尺=图上距离∶实际距离,先统一单位,再代入公式即可求解。
120米=12000厘米
比例尺:4厘米∶12000厘米
=(4÷4)∶(12000÷4)
=1∶3000
所以这幅地图的比例尺是1∶3000。
本题主要考查比例尺的公式,熟练掌握它的公式并灵活运用。
10.1∶3000000
【解析】依据“比例尺=图上距离∶实际距离”即可改写成数值比例尺。
此线段比例尺图上距离1厘米表示实际距离30千米
30千米=3000000厘米
1厘米∶3000000厘米=1∶3000000
此题主要考查比例尺的意义以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
11.√
【解析】比例尺用来表示实际距离比图上距离缩小的程度,即比例尺=图上距离÷实地距离;比例尺在表现形式上一般有数值比例尺和线段比例尺;据此判断。
比例尺是表示图上距离比实地距离缩小的程度.比例尺的可以用以下方式来表示:数字式、文字式、线段式。
如:把数值比例尺1∶:600000改成线段比例尺
因为600000厘米=6千米
则化成线段比例尺为图上距离1厘米表示实际距离是6千米,
所以改写成的线段比例尺为:
一幅地图的比例尺可以是数值比例尺,也可以是线段比例尺。原题说法正确。
故答案为:√
本题主要考查比例尺的表示形式,牢记即可。
12.×
【解析】比例尺是图上距离与实际距离的比,据此判断即可。
比例尺是图上距离与实际距离的比,而不是比值。原说法错误。
故答案为:×
明确比值是一个具体的数值,而比例尺是一个比,是解答本题的关键。
13.×
【解析】面积为100平方厘米的正方形,边长为10厘米,按1∶10的比例尺画在平面图上,图上的边长为10×=1(厘米),进而求出图上的面积即可。
10×=1(厘米);
1×1=1(平方厘米),原题说法错误。
故答案为:×
求出图上的边长是解答本题的关键。
14.×
【解析】根据比例尺的意义可知,比例尺1∶10表示图上1厘米表示实际10厘米,那么用这个比例尺画出的图形比实际要小。
由分析可知:
大林画出的示意图比原来图形大,应使用放大比例尺,所以大林使用的比例尺不可能是1∶10。原说法错误。
故答案为:×
15.×
【解析】比例尺是1∶200,表示图上距离1厘米,代表实际距离200厘米,实际距离是图上距离的200倍;设图上的正方形边长为1厘米,则实际正方形的边长为200厘米;根据正方形的面积=边长×边长,分别计算出图上的正方形面积与实际正方形面积,即可作出判断。
设图上的正方形边长为1厘米,则实际正方形的边长为200厘米。
图上的正方形的面积:1×1=1(平方厘米)
实际的正方形的面积:200×200=40000(平方厘米)
图上的正方形面积与实际正方形面积的比是1∶40000,因此原题干的说法是错误的。
故答案为:×
16.240000平方厘米.
【解析】7×100=700(厘米) 5×100=500(厘米) 高:4×100=400(厘米)
(700+500)×400÷2=1200×400÷2=240000(平方厘米)
答:这块钢板的实际面积是240000平方厘米。
17.见解析
【解析】根据比例尺先求出按1∶2的比例缩小后的图形的底和高;即6÷2=3;4÷2=2;据此画出三角形即可。
本题考查图形的放大与缩小。
18.见解析
【解析】因2∶1=2÷1=2,将平行四边形的底和高扩大到原平行四边形底和高的2倍即可;1∶3=1÷3=,将长方形的长和宽缩小为原边长的。据此解答。
本题考查了图形的放大与缩小。理解比的意义是解答此题的关键。
19.5小时
【解析】已知地图的比例尺以及合肥到上海的图上距离,根据“实际距离=图上距离÷比例尺”,求出合肥到上海的实际距离;又已知王叔叔开车的速度,根据“时间=路程÷速度”,即可求解。注意单位的换算:1千米=100000厘米。
10÷
=10×4800000
=48000000(厘米)
48000000厘米=480千米
480÷96=5(小时)
答:5小时到达。
20.1.5小时
【解析】比例尺是1∶2500000,表示图上1厘米代表实际距离2500000厘米,即25千米。已知A、B两地图上相距12厘米,用25乘12即可求出A、B两地的实际距离。相遇时间=总路程÷速度和,据此用两地的总路程除以李叔叔与王叔叔开车的速度和,即可求出几小时后两人能相遇。
2500000厘米=25千米
25×12=300(千米)
300÷(105+95)
=300÷200
=1.5(小时)
答:1.5小时后两人能相遇。
21.72千米
【解析】根据题意,结合“实际距离=图上距离÷比例尺”这一公式,求出实际距离,再根据“速度=路程÷时间”这一公式,即可求出答案。
实际距离:4÷
=4×4500000
=18000000(厘米)
18000000厘米=180千米
180÷2.5=72(千米)
答:平均每小时行驶72千米。
一、选择题
1.一个长150米,宽90米的长方形广场,画在比例尺1∶3000的图纸上,长应画( )厘米。
A.3 B.5 C.15
2.一幅图的比例尺是60∶1,它表示图上长度是实际长度的( )。
A.160 B.61倍 C.60倍 D.59倍
3.在一张图纸上,用1厘米的线段表示2毫米的实际距离,这张图纸的比例尺是( )。
A. B. C. D.
4.学校操场的长是40米,按照1∶10000的比例尺把它画在图上应画( )。
A.4分米 B.4厘米 C.4毫米
5.郑开马拉松全程约为42千米,已知地图上量得郑开马拉松全程距离为2.1厘米,这张地图的比例尺为( )
A.1:20000 B.1:200000 C.1:2000000 D.1:20000000
二、填空题
6.2021年是中国共产党成立100周年,小明打算国庆节和父母一起到北京。他在一幅比例尺为1∶20000000的地图上量得成都到北京的距离约为9厘米,成都到北京的实际距离大约是( )千米。
7.比例尺1∶2000表示的含义是图上1( )表示实际距离( )米。
8.如图,书店在学校的( )偏( )方向( ),( )千米处。
9.一幅地图,用图上的4厘米表示实际的120米,这幅地图的比例尺是( )。
10.把改写成数值比例尺是( )。
三、判断题
11.一幅地图的比例尺可以是数值比例尺,也可以是线段比例尺。( )
12.比例尺就是图上距离与实际距离的比值。( )
13.把一个面积为100平方厘米的正方形按1∶10的比例尺画在平面图上,图上的面积是10平方厘米。( )
14.大林画出的示意图比原来图形大,大林使用的比例尺可能是1∶10。( )
15.一幅平面图的比例尺是1∶200,那么图上的正方形的面积与实际正方形面积的比是1∶200。( )
四、计算题
16.如图是一块钢板按1:100缩小后画在方格纸上的图形(每小格的边长是1厘米).请你算出这块钢板的实际面积.
五、作图题
17.请在方格中按1∶2画出三角形缩小后的图形。
18.在方格纸上按要求画图。
(1)按2∶1的比画出平行四边形放大后的图形。
(2)按1∶3的比画出长方形缩小后的图形。
六、解答题
19.在新冠疫情期间,合肥的王叔叔开车去上海运送物资,他在一幅比例尺是1∶4800000的地图上,量得合肥到上海的距离大约是10厘米,王叔叔开车以每小时96千米的速度行驶,几小时到达?
20.在比例尺是1∶2500000的地图上,量得A、B两地相距12厘米。如果李叔叔和王叔叔开车同时从两地相对出发,李叔叔开车每小时行105千米,王叔叔开车每小时行95千米。几小时后两人能相遇?
21.在一幅比例尺是1∶4500000的地图上量得甲地到乙地的距离是4厘米,爸爸开车从甲地出发,沿图上的路线到乙地用了2.5小时,平均每小时行驶多少千米?
答案以及解析
1.B
【解析】由比例尺=图上距离÷实际距离可知,图上距离=实际距离×比例尺,代入数据即可解答。
150米=15000厘米
15000×=5(厘米)
即长应画5厘米。
故答案为:B
明确实际距离、图上距离和比例尺之间的关系是解答本题的关键。
2.C
【解析】因为比例尺是图上距离与实际距离的比,比例尺60∶1是一个扩大的比例尺,即图上的60cm相当于实际的1cm,所以图上距离是实际距离的60倍。
60∶1
=60÷1
=60
它表示图上长度是实际长度的60倍。
故答案为:C
此题主要考查比例尺的意义:比例尺是图上距离与实际距离的比。
3.A
【解析】按照比例尺的定义,化简图上距离1厘米与实际距离2毫米的比即可。
1厘米=10毫米
10毫米∶2毫米
=5∶1
这张图纸的比例尺是5∶1。
故答案为:A。
本题的解题关键是掌握比例尺的定义,注意换算统一单位。
4.C
【解析】根据图上距离=实际距离×比例尺,求出图上的长即可。
40米=4000厘米
4000×=0.4(厘米)=4(毫米)
故答案为:C
此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题。
5.C
【解析】试题分析:根据比例尺=图上距离:实际距离,可直接求得这张地图的比例尺.
解答:解:42千米=4200000厘米,
比例尺=2.1:4200000=1:2000000.
答:这张地图的比例尺为1:2000000.
故选C.
考查了比例尺的意义,表示比例尺的时候,注意统一单位长度.
6.1800
【解析】根据图上距离÷比例尺=实际距离,用9÷即可求出9厘米的实际距离,再把单位换算成千米。
9÷
=9×20000000
=180000000(厘米)
180000000厘米=1800千米
成都到北京的实际距离大约是1800千米。
7. 厘米 20
【解析】根据比例尺的定义,图上距离是实际距离的,据此解答即可。
因为比例尺是1∶2000,所以图上距离1厘米表示实际距离2000厘米,2000厘米=20米。
由此可得:比例尺1∶2000表示的含义是图上1厘米表示实际距离20米。
此题主要考查比例尺的意义,解答时要注意单位的换算。
8. 西 北 30° 1.8
【解析】根据图上确定方向的方法:上北下南、左西右东,以学校为观测点,确定书店的方向,然后根据图上1厘米表示实际900米,求出2厘米的实际距离,据此解答。
2×900=1800(米)
1800米=1.8千米
书店在学校的西偏北方向30°,1.8千米处。
此题主要考查依据方向(角度)和距离确定物体位置的方法。
9.1∶3000
【解析】根据比例尺=图上距离∶实际距离,先统一单位,再代入公式即可求解。
120米=12000厘米
比例尺:4厘米∶12000厘米
=(4÷4)∶(12000÷4)
=1∶3000
所以这幅地图的比例尺是1∶3000。
本题主要考查比例尺的公式,熟练掌握它的公式并灵活运用。
10.1∶3000000
【解析】依据“比例尺=图上距离∶实际距离”即可改写成数值比例尺。
此线段比例尺图上距离1厘米表示实际距离30千米
30千米=3000000厘米
1厘米∶3000000厘米=1∶3000000
此题主要考查比例尺的意义以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
11.√
【解析】比例尺用来表示实际距离比图上距离缩小的程度,即比例尺=图上距离÷实地距离;比例尺在表现形式上一般有数值比例尺和线段比例尺;据此判断。
比例尺是表示图上距离比实地距离缩小的程度.比例尺的可以用以下方式来表示:数字式、文字式、线段式。
如:把数值比例尺1∶:600000改成线段比例尺
因为600000厘米=6千米
则化成线段比例尺为图上距离1厘米表示实际距离是6千米,
所以改写成的线段比例尺为:
一幅地图的比例尺可以是数值比例尺,也可以是线段比例尺。原题说法正确。
故答案为:√
本题主要考查比例尺的表示形式,牢记即可。
12.×
【解析】比例尺是图上距离与实际距离的比,据此判断即可。
比例尺是图上距离与实际距离的比,而不是比值。原说法错误。
故答案为:×
明确比值是一个具体的数值,而比例尺是一个比,是解答本题的关键。
13.×
【解析】面积为100平方厘米的正方形,边长为10厘米,按1∶10的比例尺画在平面图上,图上的边长为10×=1(厘米),进而求出图上的面积即可。
10×=1(厘米);
1×1=1(平方厘米),原题说法错误。
故答案为:×
求出图上的边长是解答本题的关键。
14.×
【解析】根据比例尺的意义可知,比例尺1∶10表示图上1厘米表示实际10厘米,那么用这个比例尺画出的图形比实际要小。
由分析可知:
大林画出的示意图比原来图形大,应使用放大比例尺,所以大林使用的比例尺不可能是1∶10。原说法错误。
故答案为:×
15.×
【解析】比例尺是1∶200,表示图上距离1厘米,代表实际距离200厘米,实际距离是图上距离的200倍;设图上的正方形边长为1厘米,则实际正方形的边长为200厘米;根据正方形的面积=边长×边长,分别计算出图上的正方形面积与实际正方形面积,即可作出判断。
设图上的正方形边长为1厘米,则实际正方形的边长为200厘米。
图上的正方形的面积:1×1=1(平方厘米)
实际的正方形的面积:200×200=40000(平方厘米)
图上的正方形面积与实际正方形面积的比是1∶40000,因此原题干的说法是错误的。
故答案为:×
16.240000平方厘米.
【解析】7×100=700(厘米) 5×100=500(厘米) 高:4×100=400(厘米)
(700+500)×400÷2=1200×400÷2=240000(平方厘米)
答:这块钢板的实际面积是240000平方厘米。
17.见解析
【解析】根据比例尺先求出按1∶2的比例缩小后的图形的底和高;即6÷2=3;4÷2=2;据此画出三角形即可。
本题考查图形的放大与缩小。
18.见解析
【解析】因2∶1=2÷1=2,将平行四边形的底和高扩大到原平行四边形底和高的2倍即可;1∶3=1÷3=,将长方形的长和宽缩小为原边长的。据此解答。
本题考查了图形的放大与缩小。理解比的意义是解答此题的关键。
19.5小时
【解析】已知地图的比例尺以及合肥到上海的图上距离,根据“实际距离=图上距离÷比例尺”,求出合肥到上海的实际距离;又已知王叔叔开车的速度,根据“时间=路程÷速度”,即可求解。注意单位的换算:1千米=100000厘米。
10÷
=10×4800000
=48000000(厘米)
48000000厘米=480千米
480÷96=5(小时)
答:5小时到达。
20.1.5小时
【解析】比例尺是1∶2500000,表示图上1厘米代表实际距离2500000厘米,即25千米。已知A、B两地图上相距12厘米,用25乘12即可求出A、B两地的实际距离。相遇时间=总路程÷速度和,据此用两地的总路程除以李叔叔与王叔叔开车的速度和,即可求出几小时后两人能相遇。
2500000厘米=25千米
25×12=300(千米)
300÷(105+95)
=300÷200
=1.5(小时)
答:1.5小时后两人能相遇。
21.72千米
【解析】根据题意,结合“实际距离=图上距离÷比例尺”这一公式,求出实际距离,再根据“速度=路程÷时间”这一公式,即可求出答案。
实际距离:4÷
=4×4500000
=18000000(厘米)
18000000厘米=180千米
180÷2.5=72(千米)
答:平均每小时行驶72千米。
