6.1基本立体图形 高一数学北师大版2019必修第二册同步课时训练(含解析)
文档属性
| 名称 | 6.1基本立体图形 高一数学北师大版2019必修第二册同步课时训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 621.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-22 00:00:00 | ||
图片预览



文档简介
6.1 基本立体图形 高一数学北师大版2019必修第二册同步课时训练
一、选择题
1.下列说法中正确的是( )
A.棱柱的侧面可以是三角形 B.棱柱的各条棱都相等
C.所有几何体的表面都能展成平面图形 D.正方体和长方体都是特殊的四棱柱
2.如图所示的几何体,关于其结构特征,下列说法不正确的是( )
A.该几何体是由两个同底的四棱锥组成的几何体
B.该几何体有12条棱,6个顶点
C.该几何体有8个面,并且各面均为三角形
D.该几何体有9个面,其中一个面是四边形,其余均为三角形
3.下列关于棱锥 棱台的说法正确的是( )
A.有一个面是多边形,其余各面是三角形的几何体是棱锥
B.有两个面平行且相似,其他各面都是梯形的多面体是棱台
C.用一个平面去截棱锥,底面与截面之间那部分所围成的几何体叫做棱台
D.棱台的各侧棱延长后必交于一点
4.下列说法正确的是( )
A.用一平面去截圆台,截面一定是圆面
B.在圆台的上、下底面圆周上各取一点,则两点的连线就是圆台的母线
C.圆台的任意两条母线延长后相交于同一点
D.圆锥的母线可能平行
5.下面的几何体中是棱柱的有( )
A.3个 B.4个 C.5个 D.6个
6.观察下面的几何体,哪些是棱柱?( )
A.(1)(3)(5) B.(1)(2)(3)(5) C.(1)(3)(5)(6) D.(3)(4)(6)(7)
7.有以下四种说法:①棱台的两条不相邻的侧棱延长后相交于一点;②四条侧棱长都相等的棱台,一定是正四棱台;③棱台的高可以和它的某一条侧棱长相等;④有两个面是相互平行的相似多边形,其余各面都是梯形的多面体一定是棱台.其中错误说法的个数为( )
A.1 B.2 C.3 D.4
8.如图,在三棱锥中,,,为锐角,侧棱,一只小虫从A点出发,沿侧面绕棱锥爬行一周后回到A点,则小虫爬行的最短距离为( )
A. B. C. D.
9.如图,一个封闭的长方体,它的六个表面各标出A,B,C,D,E,F这六个字母,现放成下面三种不同的位置,已标明能看见的表面上的字母,则字母A,B,C对面的字母依次分别为( )
A.D,E,F B.F,D,E C.E,D,F D.E,F,D
10.下列说法正确的是( )
A.圆锥的底面是圆面,侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.圆台的任意两条母线的延长线可能相交也可能不相交
11.下面是关于三棱锥的三个说法:
①底面是等边三角形,顶点与底面中心的连线垂直于底面的三棱锥是正三棱锥;
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
其中正确说法的序号是( )
A.③ B.①② C.①③ D.①
12.给出下列说法:
①正四棱柱是正多面体;
②正四棱柱是简单多面体;
③简单多面体是凸多面体;
④以正四面体各面的中心为顶点的四面体仍然是正四面体.
其中正确的说法个数为( )
A.1 B.2 C.3 D.4
二、填空题
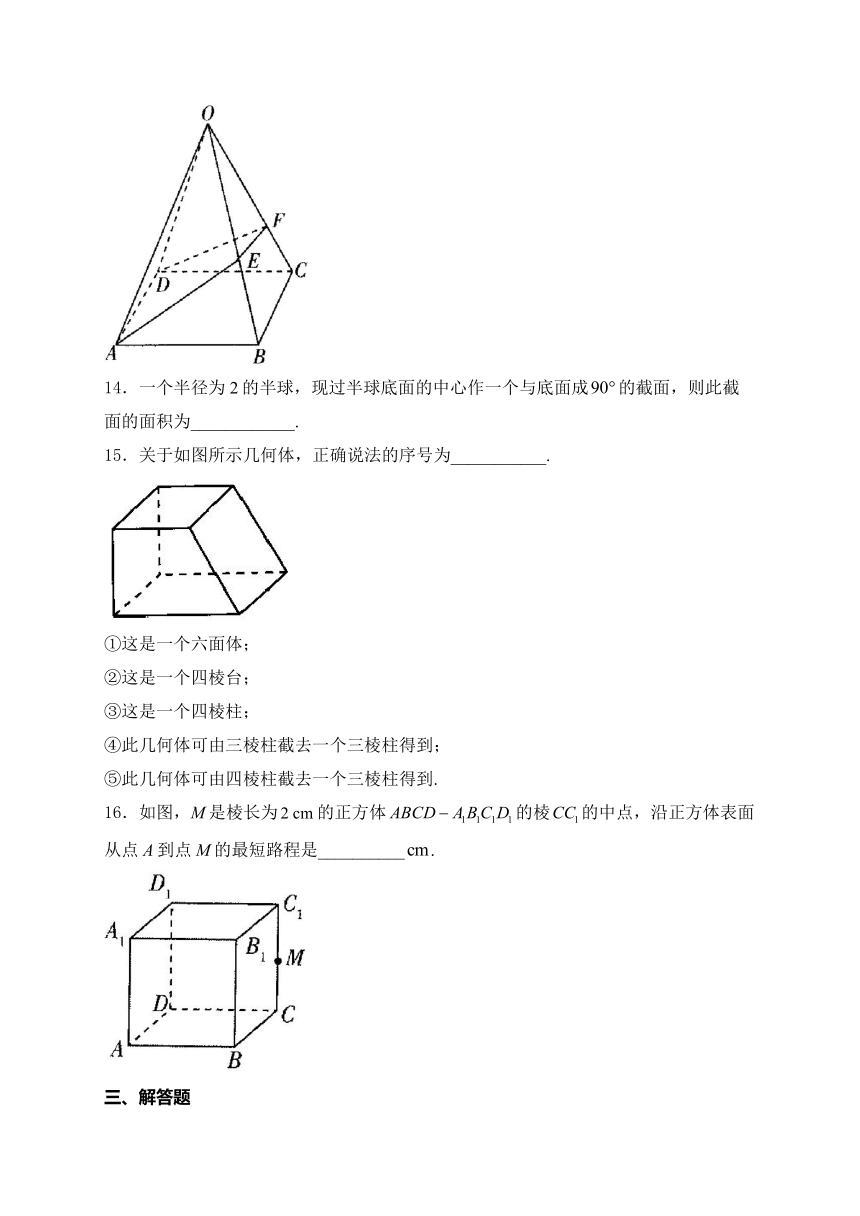
13.如图,在正四棱锥中,侧棱长均为4,且相邻两条侧棱的夹角为,E,F分别是线段OB,OC上的点,则的最小值为___________.
14.一个半径为2的半球,现过半球底面的中心作一个与底面成的截面,则此截面的面积为____________.
15.关于如图所示几何体,正确说法的序号为___________.
①这是一个六面体;
②这是一个四棱台;
③这是一个四棱柱;
④此几何体可由三棱柱截去一个三棱柱得到;
⑤此几何体可由四棱柱截去一个三棱柱得到.
16.如图,M是棱长为的正方体的棱的中点,沿正方体表面从点A到点M的最短路程是__________.
三、解答题
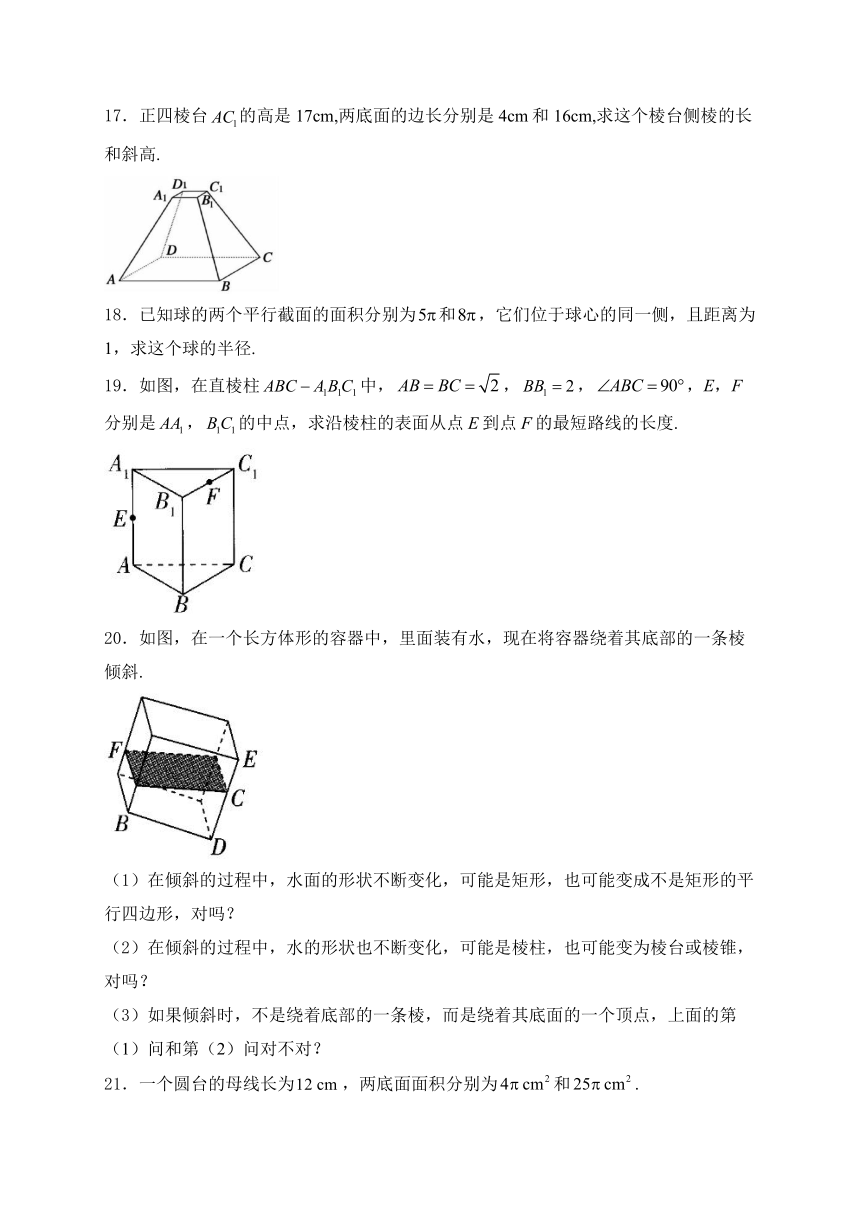
17.正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高.
18.已知球的两个平行截面的面积分别为和,它们位于球心的同一侧,且距离为1,求这个球的半径.
19.如图,在直棱柱中,,,,E,F分别是,的中点,求沿棱柱的表面从点E到点F的最短路线的长度.
20.如图,在一个长方体形的容器中,里面装有水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
21.一个圆台的母线长为,两底面面积分别为和.
(1)求圆台的高;
(2)求截得此圆台的圆锥的母线长.
22.如图,正四棱台的高是,上、下底面边长分别为和.
(1)求该棱台的侧棱长;
(2)求直线与BC的距离.
参考答案
1.答案:D
解析:棱柱的侧面都是四边形,A不正确;
棱柱的各条侧棱相等,所以B不正确;
球不能展开为平面图形,C不正确;
正方体和长方体都是特殊的四棱柱,D正确;
故选:D.
2.答案:D
解析:根据几何体直观图,得
该几何体是由两个同底的四棱锥组成的几何体,
且有棱MA,MB,MC,MD,AB,BC,CD,DA,NA,NB,NC和ND,共12条;
顶点是M,A,B,C,D和N共6个;
且有面MAB,面MBC,面MCD,面MDA,面NAB,面NBC,面NCD和面NDA共个,且每个面都是三角形.
所以选项A,B,C正确,选项D错误.
故选D.
3.答案:D
解析:有一个面是多边形,其余各面是三角形,若其余各面没有一个共同的顶点,则不是棱锥,故A错误;
两个面平行且相似,其他各面都是梯形的多面体不一定是棱台,还要满足各侧棱的延长线交于一点,故B错误,D正确;
用一个平行于底面的平面去截棱锥,底面与截面之间那部分所围成的几何体叫做棱台,故C错误.
故选:D.
4.答案:C
解析:对于A,当平面沿轴截圆台时,截面为等腰梯形,故A错误;
对于B,旋转的直角梯形不垂直于底的腰叫做圆台的母线,故B错误;
对于C,由于圆台可由一个平行于底面的平面截圆锥所得,故C正确;故D错误;
故选:C.
5.答案:C
解析:棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,
观察图形满足棱柱概念的几何体有:①②③④⑤,共五个.
故选:C.
6.答案:A
解析:根据棱柱的结构特征:一对平行的平面且侧棱相互平行的几何体,
所以棱柱有(1)(3)(5).
故选:A.
7.答案:B
解析:棱台的所有侧棱延长后都相交于一点,故①正确;
当棱台的一条侧棱垂直于底面时,其高与该侧棱长相等,故③正确;
②中的棱台尽管侧棱长相等,但缺少底面的形状,不能确定为正四棱台,故错误;如图所示可说明④是错误的.
8.答案:D
解析:根据题意,在三棱锥中,,,则有,可得,又为锐角,所以.
因为,所以,将三棱锥沿侧棱PA展开,如图,根据余弦定理,所求最短距离为,故选D.
9.答案:C
解析:正方体有3对平行的平面,根据3种摆放的形式可知,B与D,A与E,C与F是相对的平面(字母代表其所在平面).故选C.
10.答案:A
解析:A是圆锥的性质,故正确;对于B,动手操作一下,发现一张扇形的纸片只能卷成一个无底面的圆锥,故B错误;对于C,根据圆柱的结构特征可知,若两个相等的圆面不平行,那么这个物体不是圆柱,故C错误;对于D,圆台是由圆锥截得的,故其任意两条母线延长后一定交于一点,故D错误.
11.答案:D
解析:①根据正三棱锥的定义可知,①正确;②显然错误,例如当三条侧棱中仅有一条不与底面边长相等时,该三棱锥侧面都是等腰三角形,但不是正三棱锥;③底面是等边三角形,侧面的面积都相等,说明顶点到底面三边的距离(斜高)相等,根据射影长的关系,可以得到顶点在底面的射影(垂足)到底面三边所在直线的距离也相等,由于在底面所在的平面内,到底面三边所在直线的距离相等的点有4个:内心(本题的中心)1个、旁心3个,因此不能保证三棱锥是正三棱锥.故选D.
12.答案:B
解析:①正四棱柱是正多面体,是错误的,因为正四棱柱的底面是正方形,侧棱长不一定等于正方形的边长;②正四棱柱是简单多面体,是正确的,符合简单多面体的定义;③简单多面体是凸多面体,是错误的,凸多面体是简单多面体,简单多面体并不都是凸多面体;④以正四面体各面的中心为顶点的四面体仍然是正四面体,是正确的.故选B.
13.答案:
解析:如图,将正四棱锥的侧面OAB,侧面OBC,侧面OCD展开,则的最小值为AD.
在中,,,则.
所以的最小值为.
14.答案:
解析:过半球底面的中心作一个与底面成的截面,截面是半圆面,半径为2,所以其面积为.
15.答案:①③④⑤
解析:①正确,因为有六个面,属于六面体的范围;②错误,因为侧棱的延长线不能交于一点,所以不正确;③正确,如果把几何体放倒,会发现是一个四棱柱;④⑤都正确,如图所示.
16.答案:
解析:若以BC为轴展开,如图①,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为,,故A,M两点之间的距离是.
若以为轴展开,如图②,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为,,故A,M两点之间的距离是.故沿正方体表面从点A到点M的最短路程是.
17.答案:棱台的侧棱长为19cm,斜高为
解析:如图所示,设棱台的两底面的中心分别是和O,和BC的中点分别是和E,连接,,,OB,,OE,则四边形和都是直角梯形.
,,
,,,.
,
.
,.
即棱台的侧棱长为19cm,斜高为.
18.答案:3
解析:如图,作出球的轴截面.
两个平行截面的面积分别为,,
两个截面圆的半径分别为,.
又球心到两个截面的距离分别为,,且两截面位于球心的同一侧,
,解得或(舍).
故这个球的半径为3.
19.答案:
解析:因为,,所以.
由题意,知可分为以下几种情况:
(1)将侧面和展开后如图①所示.
连接EF,易知,,
所以.
(2)把上底面与侧面展开后如图②所示.
连接EF,过点E作于点M,
则,,
所以.
(3)把上底面与侧面展开后如图③所示.
连接EF,过点E作于点H,过点F作于点D,则,,
所以.
比较以上三条路线的长度,可知第三条路线的长度最短,
所以沿棱柱的表面从点E到点F的最短路线的长度为.
20、
(1)答案:不对
解析:不对.水面的形状就是用一个与棱(长方体形容器倾斜时固定不动的棱)平行的平面截长方体时截面的形状,该截面的形状一定是矩形.
(2)答案:不对
解析:不对.水的形状就是用与棱(长方体形容器倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余几何体的形状,剩余几何体一定是棱柱,水比较少时,是三棱柱,水比较多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.
(3)答案:(1)对,(2)不对
解析:用任意一个平面去截长方体,其截面形状可以是三角形、四边形、五边形或六边形,因而水面的形状可以是三角形、四边形、五边形或六边形;水的形状可能是棱锥,也可能是棱柱,但不可能是棱台.故(1)对,(2)不对.
21、
(1)答案:
解析:过圆台的轴作截面,则截面为等腰梯形,记为四边形ABCD,如图所示.作于点M.
记圆台的上、下底面的圆心分别为,O,连接.
由已知可得,,且,
所以,即圆台的高为.
(2)答案:
解析:如图,延长,,交于点S,
设截得此圆台的圆锥的母线长为,
则由,可得,得,
即截得此圆台的圆锥的母线长为.
22.答案:(1)
(2)
解析:(1)过点、分别在平面内作,,
垂足分别为点E、F,如下图所示:
根据正四棱台的性质可知四边形为等腰梯形,
因为四边形ABCD为正方形,且,则,同理,
在等腰梯形内,因为,,,
所以,四边形为矩形,所以,,,
,,,所以,,
所以,,
所以,该正四棱台的侧棱长为.
(2)过点、分别在平面内作,,垂足分别为点M、N,
在等腰梯形中,,,,
则四边形为矩形,所以,,,
,,,所以,,
则,所以,.
因此,直线与BC的距离为.
一、选择题
1.下列说法中正确的是( )
A.棱柱的侧面可以是三角形 B.棱柱的各条棱都相等
C.所有几何体的表面都能展成平面图形 D.正方体和长方体都是特殊的四棱柱
2.如图所示的几何体,关于其结构特征,下列说法不正确的是( )
A.该几何体是由两个同底的四棱锥组成的几何体
B.该几何体有12条棱,6个顶点
C.该几何体有8个面,并且各面均为三角形
D.该几何体有9个面,其中一个面是四边形,其余均为三角形
3.下列关于棱锥 棱台的说法正确的是( )
A.有一个面是多边形,其余各面是三角形的几何体是棱锥
B.有两个面平行且相似,其他各面都是梯形的多面体是棱台
C.用一个平面去截棱锥,底面与截面之间那部分所围成的几何体叫做棱台
D.棱台的各侧棱延长后必交于一点
4.下列说法正确的是( )
A.用一平面去截圆台,截面一定是圆面
B.在圆台的上、下底面圆周上各取一点,则两点的连线就是圆台的母线
C.圆台的任意两条母线延长后相交于同一点
D.圆锥的母线可能平行
5.下面的几何体中是棱柱的有( )
A.3个 B.4个 C.5个 D.6个
6.观察下面的几何体,哪些是棱柱?( )
A.(1)(3)(5) B.(1)(2)(3)(5) C.(1)(3)(5)(6) D.(3)(4)(6)(7)
7.有以下四种说法:①棱台的两条不相邻的侧棱延长后相交于一点;②四条侧棱长都相等的棱台,一定是正四棱台;③棱台的高可以和它的某一条侧棱长相等;④有两个面是相互平行的相似多边形,其余各面都是梯形的多面体一定是棱台.其中错误说法的个数为( )
A.1 B.2 C.3 D.4
8.如图,在三棱锥中,,,为锐角,侧棱,一只小虫从A点出发,沿侧面绕棱锥爬行一周后回到A点,则小虫爬行的最短距离为( )
A. B. C. D.
9.如图,一个封闭的长方体,它的六个表面各标出A,B,C,D,E,F这六个字母,现放成下面三种不同的位置,已标明能看见的表面上的字母,则字母A,B,C对面的字母依次分别为( )
A.D,E,F B.F,D,E C.E,D,F D.E,F,D
10.下列说法正确的是( )
A.圆锥的底面是圆面,侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.圆台的任意两条母线的延长线可能相交也可能不相交
11.下面是关于三棱锥的三个说法:
①底面是等边三角形,顶点与底面中心的连线垂直于底面的三棱锥是正三棱锥;
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
其中正确说法的序号是( )
A.③ B.①② C.①③ D.①
12.给出下列说法:
①正四棱柱是正多面体;
②正四棱柱是简单多面体;
③简单多面体是凸多面体;
④以正四面体各面的中心为顶点的四面体仍然是正四面体.
其中正确的说法个数为( )
A.1 B.2 C.3 D.4
二、填空题
13.如图,在正四棱锥中,侧棱长均为4,且相邻两条侧棱的夹角为,E,F分别是线段OB,OC上的点,则的最小值为___________.
14.一个半径为2的半球,现过半球底面的中心作一个与底面成的截面,则此截面的面积为____________.
15.关于如图所示几何体,正确说法的序号为___________.
①这是一个六面体;
②这是一个四棱台;
③这是一个四棱柱;
④此几何体可由三棱柱截去一个三棱柱得到;
⑤此几何体可由四棱柱截去一个三棱柱得到.
16.如图,M是棱长为的正方体的棱的中点,沿正方体表面从点A到点M的最短路程是__________.
三、解答题
17.正四棱台的高是17cm,两底面的边长分别是4cm和16cm,求这个棱台侧棱的长和斜高.
18.已知球的两个平行截面的面积分别为和,它们位于球心的同一侧,且距离为1,求这个球的半径.
19.如图,在直棱柱中,,,,E,F分别是,的中点,求沿棱柱的表面从点E到点F的最短路线的长度.
20.如图,在一个长方体形的容器中,里面装有水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
21.一个圆台的母线长为,两底面面积分别为和.
(1)求圆台的高;
(2)求截得此圆台的圆锥的母线长.
22.如图,正四棱台的高是,上、下底面边长分别为和.
(1)求该棱台的侧棱长;
(2)求直线与BC的距离.
参考答案
1.答案:D
解析:棱柱的侧面都是四边形,A不正确;
棱柱的各条侧棱相等,所以B不正确;
球不能展开为平面图形,C不正确;
正方体和长方体都是特殊的四棱柱,D正确;
故选:D.
2.答案:D
解析:根据几何体直观图,得
该几何体是由两个同底的四棱锥组成的几何体,
且有棱MA,MB,MC,MD,AB,BC,CD,DA,NA,NB,NC和ND,共12条;
顶点是M,A,B,C,D和N共6个;
且有面MAB,面MBC,面MCD,面MDA,面NAB,面NBC,面NCD和面NDA共个,且每个面都是三角形.
所以选项A,B,C正确,选项D错误.
故选D.
3.答案:D
解析:有一个面是多边形,其余各面是三角形,若其余各面没有一个共同的顶点,则不是棱锥,故A错误;
两个面平行且相似,其他各面都是梯形的多面体不一定是棱台,还要满足各侧棱的延长线交于一点,故B错误,D正确;
用一个平行于底面的平面去截棱锥,底面与截面之间那部分所围成的几何体叫做棱台,故C错误.
故选:D.
4.答案:C
解析:对于A,当平面沿轴截圆台时,截面为等腰梯形,故A错误;
对于B,旋转的直角梯形不垂直于底的腰叫做圆台的母线,故B错误;
对于C,由于圆台可由一个平行于底面的平面截圆锥所得,故C正确;故D错误;
故选:C.
5.答案:C
解析:棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,
观察图形满足棱柱概念的几何体有:①②③④⑤,共五个.
故选:C.
6.答案:A
解析:根据棱柱的结构特征:一对平行的平面且侧棱相互平行的几何体,
所以棱柱有(1)(3)(5).
故选:A.
7.答案:B
解析:棱台的所有侧棱延长后都相交于一点,故①正确;
当棱台的一条侧棱垂直于底面时,其高与该侧棱长相等,故③正确;
②中的棱台尽管侧棱长相等,但缺少底面的形状,不能确定为正四棱台,故错误;如图所示可说明④是错误的.
8.答案:D
解析:根据题意,在三棱锥中,,,则有,可得,又为锐角,所以.
因为,所以,将三棱锥沿侧棱PA展开,如图,根据余弦定理,所求最短距离为,故选D.
9.答案:C
解析:正方体有3对平行的平面,根据3种摆放的形式可知,B与D,A与E,C与F是相对的平面(字母代表其所在平面).故选C.
10.答案:A
解析:A是圆锥的性质,故正确;对于B,动手操作一下,发现一张扇形的纸片只能卷成一个无底面的圆锥,故B错误;对于C,根据圆柱的结构特征可知,若两个相等的圆面不平行,那么这个物体不是圆柱,故C错误;对于D,圆台是由圆锥截得的,故其任意两条母线延长后一定交于一点,故D错误.
11.答案:D
解析:①根据正三棱锥的定义可知,①正确;②显然错误,例如当三条侧棱中仅有一条不与底面边长相等时,该三棱锥侧面都是等腰三角形,但不是正三棱锥;③底面是等边三角形,侧面的面积都相等,说明顶点到底面三边的距离(斜高)相等,根据射影长的关系,可以得到顶点在底面的射影(垂足)到底面三边所在直线的距离也相等,由于在底面所在的平面内,到底面三边所在直线的距离相等的点有4个:内心(本题的中心)1个、旁心3个,因此不能保证三棱锥是正三棱锥.故选D.
12.答案:B
解析:①正四棱柱是正多面体,是错误的,因为正四棱柱的底面是正方形,侧棱长不一定等于正方形的边长;②正四棱柱是简单多面体,是正确的,符合简单多面体的定义;③简单多面体是凸多面体,是错误的,凸多面体是简单多面体,简单多面体并不都是凸多面体;④以正四面体各面的中心为顶点的四面体仍然是正四面体,是正确的.故选B.
13.答案:
解析:如图,将正四棱锥的侧面OAB,侧面OBC,侧面OCD展开,则的最小值为AD.
在中,,,则.
所以的最小值为.
14.答案:
解析:过半球底面的中心作一个与底面成的截面,截面是半圆面,半径为2,所以其面积为.
15.答案:①③④⑤
解析:①正确,因为有六个面,属于六面体的范围;②错误,因为侧棱的延长线不能交于一点,所以不正确;③正确,如果把几何体放倒,会发现是一个四棱柱;④⑤都正确,如图所示.
16.答案:
解析:若以BC为轴展开,如图①,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为,,故A,M两点之间的距离是.
若以为轴展开,如图②,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为,,故A,M两点之间的距离是.故沿正方体表面从点A到点M的最短路程是.
17.答案:棱台的侧棱长为19cm,斜高为
解析:如图所示,设棱台的两底面的中心分别是和O,和BC的中点分别是和E,连接,,,OB,,OE,则四边形和都是直角梯形.
,,
,,,.
,
.
,.
即棱台的侧棱长为19cm,斜高为.
18.答案:3
解析:如图,作出球的轴截面.
两个平行截面的面积分别为,,
两个截面圆的半径分别为,.
又球心到两个截面的距离分别为,,且两截面位于球心的同一侧,
,解得或(舍).
故这个球的半径为3.
19.答案:
解析:因为,,所以.
由题意,知可分为以下几种情况:
(1)将侧面和展开后如图①所示.
连接EF,易知,,
所以.
(2)把上底面与侧面展开后如图②所示.
连接EF,过点E作于点M,
则,,
所以.
(3)把上底面与侧面展开后如图③所示.
连接EF,过点E作于点H,过点F作于点D,则,,
所以.
比较以上三条路线的长度,可知第三条路线的长度最短,
所以沿棱柱的表面从点E到点F的最短路线的长度为.
20、
(1)答案:不对
解析:不对.水面的形状就是用一个与棱(长方体形容器倾斜时固定不动的棱)平行的平面截长方体时截面的形状,该截面的形状一定是矩形.
(2)答案:不对
解析:不对.水的形状就是用与棱(长方体形容器倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余几何体的形状,剩余几何体一定是棱柱,水比较少时,是三棱柱,水比较多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.
(3)答案:(1)对,(2)不对
解析:用任意一个平面去截长方体,其截面形状可以是三角形、四边形、五边形或六边形,因而水面的形状可以是三角形、四边形、五边形或六边形;水的形状可能是棱锥,也可能是棱柱,但不可能是棱台.故(1)对,(2)不对.
21、
(1)答案:
解析:过圆台的轴作截面,则截面为等腰梯形,记为四边形ABCD,如图所示.作于点M.
记圆台的上、下底面的圆心分别为,O,连接.
由已知可得,,且,
所以,即圆台的高为.
(2)答案:
解析:如图,延长,,交于点S,
设截得此圆台的圆锥的母线长为,
则由,可得,得,
即截得此圆台的圆锥的母线长为.
22.答案:(1)
(2)
解析:(1)过点、分别在平面内作,,
垂足分别为点E、F,如下图所示:
根据正四棱台的性质可知四边形为等腰梯形,
因为四边形ABCD为正方形,且,则,同理,
在等腰梯形内,因为,,,
所以,四边形为矩形,所以,,,
,,,所以,,
所以,,
所以,该正四棱台的侧棱长为.
(2)过点、分别在平面内作,,垂足分别为点M、N,
在等腰梯形中,,,,
则四边形为矩形,所以,,,
,,,所以,,
则,所以,.
因此,直线与BC的距离为.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
