人教版(2019)选择性必修第一册 1.4 实验:验证动量守恒定律 课件(共67张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修第一册 1.4 实验:验证动量守恒定律 课件(共67张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 08:09:05 | ||
图片预览










文档简介
(共67张PPT)
4.实验:验证动量守恒定律
CONTENTS
目 录
O1
新知预览
·抓必备
O2
题型研析
·破重难
O3
知能演练
·提能力
O4
三维达标
·找不足
NO.1
新知预览·抓必备
一、实验目的
1.验证动量守恒定律。
2.掌握验证动量守恒定律的实验思路和实验方法。
二、实验原理
在一维碰撞中,测出相碰撞两物体的质量m1、m2和碰撞前物体的速度v1、v2及碰撞后物体的速度v1'、v2',求出碰撞前的动量p=m1v1+m2v2及碰撞后的动量p'=m1v1'+m2v2',看碰撞前后动量是否守恒。
三、实验方案设计
方案一:研究气垫导轨上滑块碰撞时的动量守恒
(1)质量的测量:用天平测量。
(2)速度的测量:v=,式中的d为滑块上挡光板的宽度,Δt为数字计时器显示的滑块上的挡光板经过光电门的时间。
(3)碰撞情景的实现:如图所示,利用弹簧片、细绳、
弹性碰撞架、胶布、撞针、橡皮泥设计各种类型的碰撞,利用在滑块上加重物的方法改变碰撞物体的质量。
(4)器材:气垫导轨、数字计时器、滑块(带挡光板)两个、弹簧片、细绳、弹性碰撞架、胶布、撞针、橡皮泥、天平。
(5)验证的表达式:m1v1'+m2v2'=m1v1+m2v2(注意速度的矢量性)。
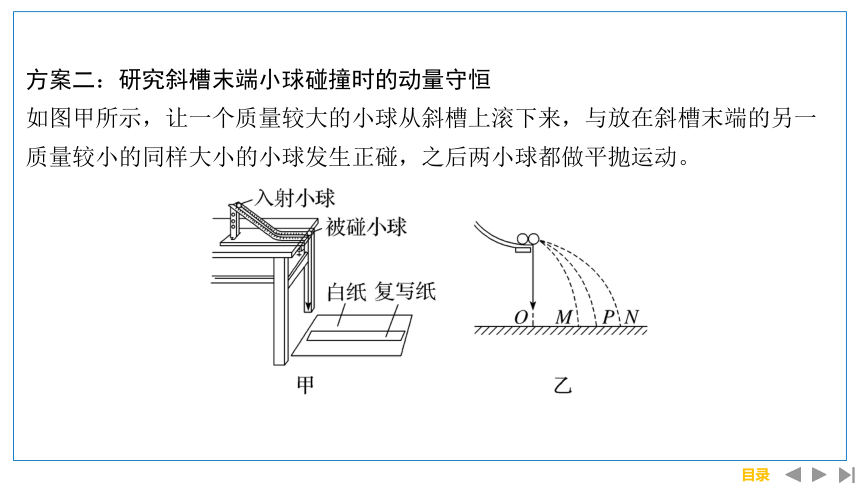
方案二:研究斜槽末端小球碰撞时的动量守恒
如图甲所示,让一个质量较大的小球从斜槽上滚下来,与放在斜槽末端的另一质量较小的同样大小的小球发生正碰,之后两小球都做平抛运动。
(1)质量的测量:用天平测量。
(2)速度的测量:由于两小球下落的高度相同,所以它们的飞行时间相等。如果以小球的飞行时间为单位时间,那么小球飞出的水平距离在数值上就等于它的水平速度。只要测出不放被碰小球时入射小球在空中飞出的水平距离OP,以及碰撞后入射小球与被碰小球在空中飞出的水平距离OM和ON,就可以表示出碰撞前后小球的速度。
(3)碰撞情景的实现(如图乙所示)
①不放被碰小球,让入射小球(测得质量为m1)从斜槽上某一位置由静止滚下,记录平抛的落点P及水平位移OP。
②在斜槽水平末端放上被碰小球(测得质量为m2),让入射
小球从斜槽同一位置由静止滚下,记下两小球离开斜槽做平抛运动的落点M、N及水平位移OM、ON。
(4)器材:斜槽、两个大小相等而质量不等的小球、重垂线、白纸、复写纸、刻度尺、天平、圆规。
(5)验证的表达式:m1·OP=m1·OM+m2·ON。
四、实验步骤
方案一:研究气垫导轨上滑块碰撞时的动量守恒
1.测量质量:用天平测出两个滑块的质量。
2.安装:正确安装好气垫导轨及有关器材。
3.实验:接通电源,进行实验,分别记录两个滑块碰撞前后经过光电门的挡光时间。
4.改变:改变滑块的质量以及改变滑块的初速度大小和方向,重复步骤3的实验。
5.结束:整理好实验器材放回原处。
方案二:研究斜槽末端小球碰撞时的动量守恒
1.测量质量:用天平测出两小球的质量,并选定质量大的小球为入射小球。
2.安装:按照图甲所示安装实验装置。调整固定斜槽使斜槽底端水平。
3.铺纸:白纸在下,复写纸在上且在适当位置铺放好。记下重垂线所指的位置O。
4.找碰前落点:不放被撞小球,每次让入射小球从斜槽上某固定高度处自由滚下,重复10次。用圆规画尽量小的圆把所有的小球落点圈在里面。圆心P就是小球落点的平均位置。
5.找碰后落点:把被撞小球放在斜槽末端,每次让入
射小球都从斜槽上步骤4中的固定高度处自由滚下,
使它们发生碰撞,重复实验10次。用步骤4的方法,
标出碰后入射小球落点的平均位置M和被撞小球落点
的平均位置N,如图丙所示。
6.结束:整理好实验器材放回原处。
五、数据处理
方案一:研究气垫导轨上滑块碰撞时的动量守恒
1.滑块速度的测量:v=,式中d为滑块上挡光片的宽度(仪器说明书上给出,也可直接测量),Δt为数字计时器显示的滑块(挡光片)经过光电门的时间。
2.验证的表达式:m1v1+m2v2=m1v1'+m2v2'。
方案二:研究斜槽末端小球碰撞时的动量守恒
1.测量线段OP、OM、ON的长度。
2.验证的表达式:m1·OP=m1·OM+m2·ON。
六、注意事项
1.碰撞的两物体应保证“水平”和“正碰”。
2.若利用方案一进行验证,调整气垫导轨时,应注意利用水平仪确保导轨水平。
3.若利用方案二进行验证:
(1)斜槽末端的切线必须水平;
(2)选质量较大的小球作为入射小球;
(3)入射小球每次都必须从斜槽同一高度由静止释放;
(4)实验过程中实验桌、斜槽、记录的白纸的位置要始终保持不变。
题型研析·破重难
NO.2
题型一 教材原型实验
【典例1】 某同学利用气垫导轨做“验证动量守恒定律”的实验,气垫导轨装置如图所示,所用的气垫导轨装置由导轨、滑块、弹射架、光电门等组成。
(1)下面是实验的主要步骤:
①安装好气垫导轨,调节气垫导轨的调节旋钮,使导轨水平;
②向气垫导轨通入压缩空气;
③接通数字计时器;
④把滑块2静止放在气垫导轨的中间;
⑤滑块1挤压导轨左端弹射架上的橡皮绳;
⑥释放滑块1,滑块1通过光电门1后与左侧带有固定弹簧(未画出)的滑块2碰撞,碰后滑块2和滑块1依次通过光电门2,两滑块通过光电门2后依次被制动;
⑦读出滑块通过光电门的挡光时间分别为:滑块1通过光电门1的挡光时间Δt1=10.01 ms,通过光电门2的挡光时间Δt2=49.99 ms,滑块2通过光电门2的挡光时间Δt3=8.35 ms;
⑧测出挡光板的宽度d=5 mm,测得滑块1的质量为m1=300 g,滑块2(包括弹簧)的质量为m2=200 g。
②碰撞前滑块1的速度v1为 m/s;碰撞后滑块1的速度v2为 m/s;碰撞后滑块2的速度v3为 m/s。(结果均保留两位有效数字)
③碰撞前系统的总动量为m1v1= 。碰撞后系统的总动量为m1v2+m2v3= 。
由此可得实验结论: 。
(2)数据处理与实验结论:
①实验中气垫导轨的作用是:
A. ;
B. 。
解析 (2)①A.大大减小了因滑块和导轨之间的摩擦而引起的误差。B.保证两个滑块的碰撞是一维的。
②滑块1碰撞之前的速度v1== m/s≈0.50 m/s;
滑块1碰撞之后的速度v2== m/s≈0.10 m/s;
滑块2碰撞之后的速度v3== m/s≈0.60 m/s;
③系统碰撞之前的总动量m1v1=0.15 kg·m/s,系统碰撞之后的总动量m1v2+m2v3=0.15 kg·m/s。
通过实验,可得结论:在实验误差允许的范围内,两滑块相互作用的过程中系统的动量守恒。
答案 见解析
【典例2】 某实验小组的同学进行“验证动量守恒定律”的实验,实验装置如图1所示。入射小球A与被碰小球B半径相同。先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹。再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自落点的痕迹。记录纸上的O点是重垂线所指的位置,M、P、N分别为落点的痕迹。
(1)本实验必须满足的条件是 ;
A.斜槽轨道是光滑的
B.斜槽轨道末端是水平的
C.A球每次从斜槽轨道同一位置由静止释放
D.测出斜槽轨道末端离地面的高度,从而计算出平抛运动时间
解析 (1)只要小球离开轨道做平抛运动就行,所以斜槽轨道是否光滑都可以,故A错误;为保证小球做平抛运动,斜槽轨道末端必须水平,故B正确;要保证碰撞前速度相同,则必须A球每次从斜槽轨道同一位置由静止释放,故C正确;本实验不需要测量平抛运动的时间,故D错误。
答案 (1)BC
(2)在两球碰撞后,为使A球不反弹,所选用的两小球质量关系应为mA mB(选填“小于”“大于”或“等于”);
解析 (2)为防止两球碰撞后入射球反弹,入射球质量应大于被碰球质量,故A球质量大于B球的质量。
答案 (2)大于
(3)实验中用天平测量出入射小球和被碰小球的质量mA、mB,验证动量守恒定律的表达式为(用图1中的字母表示)
;
解析 (3)要验证动量守恒定律,则mAv0=mAv1+mBv2,小球离开轨道后做平抛运动,抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以时间t得mAv0t=mAv1t+mBv2t,即mAOP=mAOM+mBON。
答案 (3)mAOP=mAOM+mBON
(4)某次实验中得出的落点情况如图2所示,假设碰撞过程中动量守恒,则入射小球质量mA和被碰小球质量mB之比为 。
解析 (4)如图2所示,代入上式得mA×22.50=mA×12.50+mB×35.00,解得mA:mB=7:2。
答案 (4)7:2
题型二 拓展与创新实验
【典例3】 某班物理兴趣小组选用如图所示的装置来“验证动量守恒定律”。将一段不可伸长的轻质绳一端与力传感器(可以实时记录绳所受的拉力)相连固定在O点,另一端连接小钢球A,把小钢球拉至M处可使绳水平拉紧。在小钢球最低点N右侧放置有一水平气垫导轨,气垫导轨上放有小滑块B(B上安装宽度较小且质量不计的遮光板)、光电门(已连接数字毫秒计),当地的重力加速度为g。
某同学按图所示安装气垫导轨、滑块B(调整滑块B的位置使小钢球自由下垂静止在N点时与滑块B接触而无压力)和光电门,调整好气垫导轨高度,确保小钢球A通过最低点时恰好与滑块B发生正碰。让小钢球A从某位置释放,摆到最低点N与滑块B碰撞,碰撞后小钢球A并没有反向,碰撞时间极短。
(1)为完成实验,除了毫秒计读数Δt、碰撞前瞬间绳的拉力F1、碰撞结束瞬间绳的拉力F2、滑块B质量mB和遮光板宽度d外,还需要测量的物理量有 。(用题中已给的物理量符号来表示)
A.小钢球A质量mA
B.绳长L
C.小钢球从M到N运动的时间
解析 (1)滑块B通过光电门时的瞬时速度vB=,根据牛顿第二定律得F1-mAg=mA,F2-mAg=mA,根据动量守恒定律得mAv1=mAv2+mBvB,整理得=+mB,所以还需要测量A的质量mA以及绳长L,故选A、B。
答案 (1)AB
(2)滑块B通过光电门时的瞬时速度vB= 。(用题中已给的物理量符号来表示)
解析 (2)滑块B通过光电门时的瞬时速度vB=。
答案 (2)
(3)实验中的动量守恒定律的表达式是 。(用题中已给的物理量符号来表示)
解析 (3)由(1)中分析可知,实验中的动量守恒定律的表达式是=+mB。
答案 (3)=+mB
如图所示,气垫导轨是常用的一种实验仪器。它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦。我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:
a.用天平分别测出滑块A、B的质量mA、mB;
b.调整气垫导轨,使导轨 ;
c.在滑块A、滑块B间放入一个被压缩的轻弹簧,用电动卡销锁定,静止放置在气垫导轨上;
d.用刻度尺测出滑块A的左端至挡板C的距离L1,B的右端至挡板D的距离L2;
e.按下电钮放开卡销,同时使分别记录滑块A、B运动时间的计时器开始工作,当滑块A、B分别碰撞挡板C、D时停止计时,记下滑块A、B分别到达挡板C、D的运动时间t1和t2。
(1)步骤b补充完整。
解析:(1)为保证A、B作用过程中系统动量守恒,应调整气垫导轨,使导轨水平。
答案:(1)水平
(2)利用上述测量的实验数据,验证动量守恒定律的表达式是 。
解析:(2)弹簧恢复原长后,A、B做匀速直线运动,A的速度大小为vA=,B的速度大小为vB=,以向左的方向为正方向,由动量守恒定律得mAvA-mBvB=0,由以上各式得mA-mB=0。
答案:(2)mA-mB=0
(3)利用上述实验数据还能测出被压缩弹簧的弹性势能的大小,其表达式是Ep= 。
解析:(3)由能量守恒定律得,被压缩弹簧的弹性势能Ep=mA+mB=mA+mB。
答案:(3)mA+mB
知能演练·提能力
NO.3
1.在用气垫导轨做“验证动量守恒定律”的实验时,
左侧滑块质量m1=200 g,右侧滑块质量m2=160 g,
挡光片宽度为3.00 cm,两滑块之间有一压缩的弹簧片,并用细线将两滑块连在一起,如图所示。开始时两滑块静止,烧断细线后,两滑块分别向左、右方向运动。挡光片通过光电门的时间分别为Δt1=0.30 s,Δt2=0.24 s。则烧断细线后两滑块的速度大小分别为v1'= m/s,v2'= m/s。烧断细线前两滑块动量之和为 kg·m/s,烧断细线后两滑块动量之和为 kg·m/s。可得到的结论是
。
解析:由平均速度公式可得v1'== m/s=0.1 m/s,v2'== m/s=0.125 m/s;因烧断细线之前,两滑块均静止,故烧断细线前两滑块动量之和为0;设向左为正方向,烧断细线后两滑块动量之和为0.2×0.1 kg·m/s+0.16×(-0.125)kg·m/s≈0;故烧断细线前后两滑块动量之和相等,烧断细线前、后,系统动量守恒。
答案:0.1 0.125 0 0 烧断细线前、后,系统动量守恒
2.“验证动量守恒定律”实验装置如图所示,让质量为m1的小球A从斜槽上的某一位置自由滚下,与静止在支柱上大小相等、质量为m2的小球B发生碰撞。(球A运动到水平槽末端时刚好与B球发生碰撞)
(1)安装轨道时,要求轨道末端 。
解析:(1)为了保证每次小球都做平抛运动,则需要轨道的末端水平。
答案:(1)水平
(2)两小球的质量应满足m1 (选填“>”“<”或“=”)m2。
解析:(2)验证碰撞中的动量守恒定律实验,为防止入射球反弹,入射球的质量应大于被碰球的质量,即m1>m2。
答案:(2)>
(3)用游标卡尺测量小球直径时的读数如图所示,则小球的直径d= cm。
解析:(3)游标卡尺读数为10 mm+4×0.1 mm=10.4 mm=1.04 cm。
答案:(3)1.04
(4)实验中还应测量的物理量是 。
A.两小球的质量m1和m2
B.小球A的初始高度h
C.轨道末端切线离地面的高度H
D.两小球平抛运动的时间t
E.球A单独滚下时的落地点P与O点的距离xOP
F.碰后A、B两小球的落地点M、N与O点的距离xOM和xON
解析:(4)小球离开轨道后做平抛运动,它们抛出点的高度相同,在空中的运动时间t相等,两球碰撞动量守恒,有m1v1=m1v1'+m2v2',
两边同时乘时间t,则m1v1t=m1v1't+m2v2't,
根据落点可化简为m1·xOP=m1·xOM+m2·(xON-d),则实验还需要测出:两小球的质量m1和m2,球A单独滚下时的落地点P点到O点的距离xOP和碰后A、B两小球的落地点M、N与O点的距离xOM和xON,故选A、E、F。
答案:(4)AEF
(5)若碰撞中动量守恒,根据图中各点间的距离,下列式子成立的是 。
A.= B.=
C.= D.=
解析:(5)根据动量守恒定律可得m1·xOP=m1·xOM+m2·,即==,故B正确。
答案:(5)B
3.如图甲所示,在做验证动量守恒定律实验时,在小车A的前端粘有橡皮泥,推动小车A使之做匀速运动,然后与原来静止在前方的小车B相碰并粘合成一体,继续做匀速运动。在小车A后连着纸带,电磁打点计时器的电源频率为50 Hz,长木板右端下面垫放小木片用以补偿阻力。
解析:(1)实验开始前需要补偿阻力,因为只有补偿阻力后,碰撞过程中系统所受的合外力为0,动量才守恒。补偿阻力的方法是长木板右端垫高,轻推小车A,当打出的纸带点迹均匀说明已补偿阻力。
答案:(1)需要 因为只有补偿阻力后,碰撞过程中系统所受的合外力为0,动量才守恒 长木板右端垫高,轻推小车A,当打出的纸带点迹均匀说明已补偿阻力
(1)实验开始前 (选填“需要”或“不需要”)补偿阻力,理由是 ,
方法是 。
(2)若打点纸带如图乙所示,并测得各计数点间距(已标在图上)。A为打下的第一点,则应选 段来计算A的碰前速度,应选 段来计算A和B碰后的共同速度。(以上两空选填“AB”“BC”“CD”或“DE”)
解析:(2)推动小车由静止开始运动,小车有个加速过程,在碰撞前做匀速直线运动,即在相同的时间内通过的位移相同,故BC段为匀速运动的阶段,故选BC段计算碰前的速度。碰撞过程是一个变速运动的过程,而A和B碰后共同运动时做匀速直线运动,故在相同的时间内通过相同的位移,故应选DE段来计算碰后共同的速度。
答案:(2)BC DE
(3)已测得小车A的质量m1=0.40 kg,小车B的质量m2=0.20 kg,由以上测量结果可得碰前总动量为 kg·m/s,碰后总动量为 kg·m/s。实验结论: 。(计算结果保留三位有效数字)
解析:(3)A碰前的速度v1== m/s=3.15 m/s,
碰后共同速度v2== m/s=2.085 m/s,
碰前总动量p1=m1v1=0.40×3.15 kg·m/s=1.26 kg·m/s
碰后的总动量p2=(m1+m2)v2=0.60×2.085 kg·m/s≈1.25 kg·m/s
说明在误差允许的范围内,碰撞前后总动量守恒。
答案:(3)1.26 1.25 在误差允许的范围内,碰撞前后总动量守恒
4.用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,细线与竖直线之间夹角为α;A球由静止释放,摆到最低点时恰与B球发生正碰,碰撞后,A球摆到与竖直方向夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,用来记录球B的落点,B球飞行的水平距离为x。
(1)用图中所示各个物理量的符号表示:碰撞前A球的速度vA= ;碰撞后B球的速度vB= ;
解析:(1)A球从静止释放到与B球碰撞的过程,根据动能定理,有
mAg(L-Lcosα)=mA
解得vA=
碰撞后B球做平抛运动,在竖直方向有H=gt2
在水平方向有x=vBt
联立解得vB=x。
答案:(1) x
(2)探究守恒量的表达式为 。
解析:(2)若A、B碰撞的过程中动量守恒有
mAvA=mAvA'+mBvB
从碰撞结束到A球摆到最高点,根据动能定理,有
-mAg(L-Lcos β)=-mAvA'2
解得vA'=
则探究守恒量的表达式为mA=mA+mBx。
答案:(2)mA=mA+mBx
三维达标·找不足
NO.4
1.(2022·浙江义乌高二期中)某同学用如图所示的装置“验证动量守恒定律”并测量处于压缩状态下的弹簧的弹性势能。实验前,用水平仪先将光滑操作台的台面调为水平。其实验步骤为:
A.用天平测出滑块A、B的质量mA、mB;
B.用细线将滑块A、B连接,使A、B间的弹簧处于压缩状态;
C.剪断细线,滑块A、B离开弹簧后均沿光滑操作台的台面运动,最后都滑离台面,记录A、B滑块的落地点M、N;
D.用刻度尺测出M、N距操作台边缘的水平距离x1、x2;
E.用刻度尺测出操作台面距地面的高度h。
请根据实验步骤完成下面填空:
(1)滑块A、B都离开桌面后,在空中运动的时间tA tB (选填“>”“<”或“=”);
解析:(1)滑块A、B都离开桌面后做平抛运动,竖直方向高度相同,由h=gt2知tA=tB=。
答案:(1)=
(2)如果滑块A、B组成的系统动量守恒,须满足的关系是 (用测量的物理量表示);
解析:(2)根据动量守恒定律有mAvA=mBvB
又tA=tB
可得mAx1=mBx2。
答案:(2)mAx1=mBx2
(3)剪断细线前,弹簧处于压缩状态下的弹性势能是 (用测量的物理量和重力加速度g表示)。
解析:(3)根据能量守恒定律得Ep=mA+mB
又vA=,vB=
联立解得Ep=。
答案:(3)
2.(2022·浙江杭十四中高二期中)用如图甲所示的装置研究碰撞中的动量守恒,小车P的前端、小车Q的后端均粘有橡皮泥,小车P的后端连接通过打点计时器的纸带,在长木板右端垫放木块以平衡摩擦力,推一下小车P,使之运动,与静止的小车Q相碰粘在一起,继续运动。
(1)实验获得的一条纸带如图乙所示,根据点迹的不同特征把纸带上的点进行了区域划分,用刻度尺测得B、C、D、E各点到起点A的距离。根据碰撞前后小车的运动情况,应选纸带上 段来计算小车P的碰撞前的速度。
解析:(1)小车P碰撞前做匀速直线运动,在相等时间内运动位移相等,由图乙所示纸带可知,应选择纸带上的BC段求出小车P碰撞前的速度。
答案:(1)BC
(2)测得小车P(含橡皮泥)的质量为m1,小车Q(含橡皮泥)的质量为m2,如果实验数据满足关系式 ,则说明小车P、Q组成的系统碰撞前后动量守恒。
解析:(2)设打点计时器打点时间间隔为T,由图乙所示的纸带可知,碰撞前小车的速度v=,碰撞后两小车的共同速度v'=,如果碰撞前后系统动量守恒,则m1v=(m1+m2)v',即m1=(m1+m2),整理得=。
答案:(2)=
(3)如果在测量小车P的质量时,忘记粘橡皮泥,则所测系统碰撞前总动量与系统碰撞后总动量相比,将 (选填“偏大”“偏小”或“相等”)。
解析:(3)如果在测量小车P的质量时,忘记粘橡皮泥,则小车P质量的测量值小于真实值,由(2)中表达式可知,所测系统碰撞前总动量小于碰撞后系统的总动量。
答案:(3)偏小
3.(2022·浙江宁波高二期末)某物理兴趣小组利用如图甲所示的装置进行“验证动量守恒定律”的实验。在足够大的水平平台上的A点放置一个光电门,水平平台上A点右侧摩擦很小,可忽略不计,左侧为粗糙水平面。实验步骤如下:
A.在小滑块a上固定一个宽度为d的窄挡光片;
B.用天平分别测出小滑块a(含挡光片)和小球b的质量ma、mb;
C.a和b用细线连接,中间夹一被压缩了的水平轻质短弹簧,静止放置在平台上;
D.烧断细线后,a、b瞬间被弹开,并向相反方向运动;
E.记录滑块a通过光电门时挡光片的遮光时间t;
F.小球b从平台边缘飞出后,落在水平地面的B点,用刻度尺测出平台距水平地面的高度h及平台边缘重垂线与B点之间的水平距离xb;
G.改变弹簧压缩量,进行多次测量。
(1)用螺旋测微器测量挡光片的宽度,如图乙所示,则挡光片的宽度为 mm。
解析:(1)螺旋测微器的固定刻度读数为2.5 mm,可动刻度读数为5.0×0.01 mm=0.050 mm,所以最终读数为2.5 mm+0.050 mm=2.550 mm。
答案:(1)2.550
(2)该实验要验证动量守恒定律,则只需验证两物体a、b弹开后的动量大小相等,即 = 。(用上述实验所涉及物理量的字母表示,当地重力加速度为g)
解析:(2)烧断细线后,a向左运动,经过光电门,根据速度公式可知,a经过光电门的速度为va=,故a的动量大小为pa=ma。b离开平台后做平抛运动,根据平抛运动规律可得h=gt2,xb=vbt,解得vb=xb,b的动量大小为pb=mbxb,若动量守恒,设向右为正,则有0=mbvb-mava,即ma=mbxb。
答案:(2) mbxb
4.在“验证动量守恒定律”实验中,实验装置如图所示,按照以下步骤进行操作:
①在平木板表面钉上白纸和复写纸,并将该木板竖直立于紧靠槽口处,将小球a从斜槽轨道上固定点处由静止释放,撞到木板并在白纸上留下痕迹O;
②将木板水平向右移动一定距离并固定,再将小球a从固定点处由静止释放,撞到木板上得到痕迹B;
③把小球b静止放在斜槽轨道水平段的最右端,让小球a仍从固定点处由静止释放,和小球b相碰后,两球撞在木板上得到痕迹A和C。
(1)下列措施可减小实验误差的是 。
A.斜槽轨道必须是光滑的
B.每次实验均重复几次后,再记录平均落点
C.a球和b球的半径和质量满足ra=rb和ma<mb
解析:(1)本实验是“验证动量守恒定律”的,所以实验误差与斜槽轨道的光滑程度无关,A错误;每次实验均重复几次后,再记录平均落点,这样可减小实验误差,B正确;要产生正碰,a球和b球的半径需满足ra=rb,为防止两球碰撞后a球反弹,质量要满足ma>mb,C错误。
答案:(1)B
(2)为完成本实验,必须测量的物理量有 。
A.a球开始释放的高度h
B.木板水平向右移动的距离L
C.a球和b球的质量ma、mb
D.O点到A、B、C三点的距离y1、y2、y3
解析:(2)每次a球释放的高度h确定不变就可以,不用测量h值,A错误;因为小球每次打在木板上时,水平方向的位移相等,所以不需测量木板水平向右移动的距离L,B错误;要验证动量守恒定律,必须测量a球和b球的质量ma、mb,C正确;需要计算小球运动的时间,则要测量O点到A、B、C三点的距离y1、y2、y3,D正确。
答案:(2)CD
(3)只要验证等式 成立,即表示碰撞中动量守恒。[用(2)中测量的物理量表示]
解析:(3)a、b两球碰撞后做平抛运动,由L=vt和y=gt2,可得v=
则由动量守恒定律可得mav0=mav1+mbv2
即ma=ma+mb
整理得=+
若表达式=+成立,即表示碰撞中动量守恒。
答案:(3)=+
5.如图所示,用“碰撞实验器”可以验证动量守恒定律,实验时先让入射小球从特殊材料制成的光滑轨道上某一固定位置S由静止开始滚下,从轨道末端O点水平抛出,落到与轨道O点连接的斜面上,记下小球与斜面第一次碰撞留下的落点痕迹。再把被碰小球放在斜槽轨道末端,让入射小球仍从位置S由静止滚下,与被碰小球碰撞后都落到斜面上,记下两小球与斜面第一次碰撞留下的落点痕迹。每组实验都是从O点沿斜面向下依次标记M、P、N为三个落点的位置(不考虑小球在斜面上的多次碰撞,小球可视作质点),O点与各落点的距离为LOM、LOP、LON,入射小球A的质量是被碰小球B的质量的4倍。[第(2)(3)问均用LOM、LOP、LON表示]
解析:(1)若动量守恒则满足4mv0=4mv1+mv2,因为小球离开斜槽做平抛运动时,由tan θ=,可得小球在斜面上的位移x==v2∝v2,所以v∝,可得4=4+,若该碰撞是弹性碰撞,还应满足的关系式为×4m=×4m+m,可得4LOP=4LOM+LON。
答案:(1)4=4+ 4LOP=4LOM+LON
(1)第一组同学选择A球为入射球,B为被碰球,若满足关系式 ,则可以认为两球碰撞前后总动量守恒。若该碰撞是弹性碰撞,还应满足的关系式为 。
(2)第二组同学选择B球为入射球,A为被碰球,若该碰撞是弹性碰撞,则能说明两球碰撞前后总动量守恒的关系式为 。
解析:(2)若选择B球为入射球,A为被碰球,若发生弹性碰撞,则mv0=mv1'+4mv2',m=mv1'2+·4mv2'2,解得v1'=-0.6v0,v2'=0.4v0,即入射球B应该反向弹回到斜槽上后向下运动再做平抛落在斜面上,因B做平抛的速度较A大,可知B将落在N点,A将落在M点,此时动量守恒表达式应该为m=-m+4m,即4=+。
答案:(2)4=+
6.某实验小组利用如图所示的实验装置验证动量守恒定律。实验的主要步骤如下:
①用游标卡尺测量小球A、B的直径d,用毫米刻度尺测量细线的长度L,用天平测量小球A、B的质量分别为m1、m2;
②用两条细线分别将球A、B悬挂于同一水平高度,且自然下垂时两球恰好相切,球心位于同一水平线上;
③将球A向左拉起使其细线与竖直方向的夹角为α时由静止释放,与球B碰撞后,测得球A向左摆到最高点时其细线与竖直方向的夹角为θ1,球B向右摆到最高点时其细线与竖直方向的夹角为θ2。
回答下列问题:
(1)在实验步骤中,有多余操作过程的步骤是 ;
解析:(1)小球碰撞后由动能定理得
mg(L-Lcos θ)=mv2
解得v=
由动量守恒定律表达式可知细线的长度可以约掉,所以不必测量,故有多余操作的步骤是①;
答案:(1)①
(2)为保证A碰撞后向左摆动,则A、B两球质量应满足m1 m2(填“>”“<”或“=”);
解析:(2)为使A球碰撞后能反弹,则A、B两球质量应满足m1<m2;
答案:(2)<
(3)若两球碰撞前后动量守恒,则= (用③中测量的量表示);
解析:(3)小球A下摆过程中只有重力做功,机械能守恒,由机械能守恒定律得
m1=m1gL(1-cos α)
碰撞后,对A、B两小球摆动过程中只有重力作用,机械能守恒,对A有m1v1'2=m1gL(1-cos θ1)
对B有m2=m2gL(1-cos θ2)
若两球碰撞过程系统动量守恒,以水平向右为正方向,由动量守恒定律得
m1v1=-m1v1'+m2v2
解得m1=-m1+m2
则=;
答案:(3)
(4)若两球的碰撞为弹性碰撞,并且碰撞之后两个小球摆到最高点时其细线与竖直方向的夹角θ1=θ2,则= ,并且cos θ1=cos θ2= (用α表示)。
解析:(4)若是弹性碰撞,则还满足机械能守恒定律,由动量守恒定律和机械能守恒定律得
m1v1=-m1v1'+m2v2
m1=m1v1'2+m2
又θ1=θ2
联立解得=,cos θ1=cos θ2=。
答案:(4)
感谢您的耐心观看
4.实验:验证动量守恒定律
CONTENTS
目 录
O1
新知预览
·抓必备
O2
题型研析
·破重难
O3
知能演练
·提能力
O4
三维达标
·找不足
NO.1
新知预览·抓必备
一、实验目的
1.验证动量守恒定律。
2.掌握验证动量守恒定律的实验思路和实验方法。
二、实验原理
在一维碰撞中,测出相碰撞两物体的质量m1、m2和碰撞前物体的速度v1、v2及碰撞后物体的速度v1'、v2',求出碰撞前的动量p=m1v1+m2v2及碰撞后的动量p'=m1v1'+m2v2',看碰撞前后动量是否守恒。
三、实验方案设计
方案一:研究气垫导轨上滑块碰撞时的动量守恒
(1)质量的测量:用天平测量。
(2)速度的测量:v=,式中的d为滑块上挡光板的宽度,Δt为数字计时器显示的滑块上的挡光板经过光电门的时间。
(3)碰撞情景的实现:如图所示,利用弹簧片、细绳、
弹性碰撞架、胶布、撞针、橡皮泥设计各种类型的碰撞,利用在滑块上加重物的方法改变碰撞物体的质量。
(4)器材:气垫导轨、数字计时器、滑块(带挡光板)两个、弹簧片、细绳、弹性碰撞架、胶布、撞针、橡皮泥、天平。
(5)验证的表达式:m1v1'+m2v2'=m1v1+m2v2(注意速度的矢量性)。
方案二:研究斜槽末端小球碰撞时的动量守恒
如图甲所示,让一个质量较大的小球从斜槽上滚下来,与放在斜槽末端的另一质量较小的同样大小的小球发生正碰,之后两小球都做平抛运动。
(1)质量的测量:用天平测量。
(2)速度的测量:由于两小球下落的高度相同,所以它们的飞行时间相等。如果以小球的飞行时间为单位时间,那么小球飞出的水平距离在数值上就等于它的水平速度。只要测出不放被碰小球时入射小球在空中飞出的水平距离OP,以及碰撞后入射小球与被碰小球在空中飞出的水平距离OM和ON,就可以表示出碰撞前后小球的速度。
(3)碰撞情景的实现(如图乙所示)
①不放被碰小球,让入射小球(测得质量为m1)从斜槽上某一位置由静止滚下,记录平抛的落点P及水平位移OP。
②在斜槽水平末端放上被碰小球(测得质量为m2),让入射
小球从斜槽同一位置由静止滚下,记下两小球离开斜槽做平抛运动的落点M、N及水平位移OM、ON。
(4)器材:斜槽、两个大小相等而质量不等的小球、重垂线、白纸、复写纸、刻度尺、天平、圆规。
(5)验证的表达式:m1·OP=m1·OM+m2·ON。
四、实验步骤
方案一:研究气垫导轨上滑块碰撞时的动量守恒
1.测量质量:用天平测出两个滑块的质量。
2.安装:正确安装好气垫导轨及有关器材。
3.实验:接通电源,进行实验,分别记录两个滑块碰撞前后经过光电门的挡光时间。
4.改变:改变滑块的质量以及改变滑块的初速度大小和方向,重复步骤3的实验。
5.结束:整理好实验器材放回原处。
方案二:研究斜槽末端小球碰撞时的动量守恒
1.测量质量:用天平测出两小球的质量,并选定质量大的小球为入射小球。
2.安装:按照图甲所示安装实验装置。调整固定斜槽使斜槽底端水平。
3.铺纸:白纸在下,复写纸在上且在适当位置铺放好。记下重垂线所指的位置O。
4.找碰前落点:不放被撞小球,每次让入射小球从斜槽上某固定高度处自由滚下,重复10次。用圆规画尽量小的圆把所有的小球落点圈在里面。圆心P就是小球落点的平均位置。
5.找碰后落点:把被撞小球放在斜槽末端,每次让入
射小球都从斜槽上步骤4中的固定高度处自由滚下,
使它们发生碰撞,重复实验10次。用步骤4的方法,
标出碰后入射小球落点的平均位置M和被撞小球落点
的平均位置N,如图丙所示。
6.结束:整理好实验器材放回原处。
五、数据处理
方案一:研究气垫导轨上滑块碰撞时的动量守恒
1.滑块速度的测量:v=,式中d为滑块上挡光片的宽度(仪器说明书上给出,也可直接测量),Δt为数字计时器显示的滑块(挡光片)经过光电门的时间。
2.验证的表达式:m1v1+m2v2=m1v1'+m2v2'。
方案二:研究斜槽末端小球碰撞时的动量守恒
1.测量线段OP、OM、ON的长度。
2.验证的表达式:m1·OP=m1·OM+m2·ON。
六、注意事项
1.碰撞的两物体应保证“水平”和“正碰”。
2.若利用方案一进行验证,调整气垫导轨时,应注意利用水平仪确保导轨水平。
3.若利用方案二进行验证:
(1)斜槽末端的切线必须水平;
(2)选质量较大的小球作为入射小球;
(3)入射小球每次都必须从斜槽同一高度由静止释放;
(4)实验过程中实验桌、斜槽、记录的白纸的位置要始终保持不变。
题型研析·破重难
NO.2
题型一 教材原型实验
【典例1】 某同学利用气垫导轨做“验证动量守恒定律”的实验,气垫导轨装置如图所示,所用的气垫导轨装置由导轨、滑块、弹射架、光电门等组成。
(1)下面是实验的主要步骤:
①安装好气垫导轨,调节气垫导轨的调节旋钮,使导轨水平;
②向气垫导轨通入压缩空气;
③接通数字计时器;
④把滑块2静止放在气垫导轨的中间;
⑤滑块1挤压导轨左端弹射架上的橡皮绳;
⑥释放滑块1,滑块1通过光电门1后与左侧带有固定弹簧(未画出)的滑块2碰撞,碰后滑块2和滑块1依次通过光电门2,两滑块通过光电门2后依次被制动;
⑦读出滑块通过光电门的挡光时间分别为:滑块1通过光电门1的挡光时间Δt1=10.01 ms,通过光电门2的挡光时间Δt2=49.99 ms,滑块2通过光电门2的挡光时间Δt3=8.35 ms;
⑧测出挡光板的宽度d=5 mm,测得滑块1的质量为m1=300 g,滑块2(包括弹簧)的质量为m2=200 g。
②碰撞前滑块1的速度v1为 m/s;碰撞后滑块1的速度v2为 m/s;碰撞后滑块2的速度v3为 m/s。(结果均保留两位有效数字)
③碰撞前系统的总动量为m1v1= 。碰撞后系统的总动量为m1v2+m2v3= 。
由此可得实验结论: 。
(2)数据处理与实验结论:
①实验中气垫导轨的作用是:
A. ;
B. 。
解析 (2)①A.大大减小了因滑块和导轨之间的摩擦而引起的误差。B.保证两个滑块的碰撞是一维的。
②滑块1碰撞之前的速度v1== m/s≈0.50 m/s;
滑块1碰撞之后的速度v2== m/s≈0.10 m/s;
滑块2碰撞之后的速度v3== m/s≈0.60 m/s;
③系统碰撞之前的总动量m1v1=0.15 kg·m/s,系统碰撞之后的总动量m1v2+m2v3=0.15 kg·m/s。
通过实验,可得结论:在实验误差允许的范围内,两滑块相互作用的过程中系统的动量守恒。
答案 见解析
【典例2】 某实验小组的同学进行“验证动量守恒定律”的实验,实验装置如图1所示。入射小球A与被碰小球B半径相同。先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹。再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自落点的痕迹。记录纸上的O点是重垂线所指的位置,M、P、N分别为落点的痕迹。
(1)本实验必须满足的条件是 ;
A.斜槽轨道是光滑的
B.斜槽轨道末端是水平的
C.A球每次从斜槽轨道同一位置由静止释放
D.测出斜槽轨道末端离地面的高度,从而计算出平抛运动时间
解析 (1)只要小球离开轨道做平抛运动就行,所以斜槽轨道是否光滑都可以,故A错误;为保证小球做平抛运动,斜槽轨道末端必须水平,故B正确;要保证碰撞前速度相同,则必须A球每次从斜槽轨道同一位置由静止释放,故C正确;本实验不需要测量平抛运动的时间,故D错误。
答案 (1)BC
(2)在两球碰撞后,为使A球不反弹,所选用的两小球质量关系应为mA mB(选填“小于”“大于”或“等于”);
解析 (2)为防止两球碰撞后入射球反弹,入射球质量应大于被碰球质量,故A球质量大于B球的质量。
答案 (2)大于
(3)实验中用天平测量出入射小球和被碰小球的质量mA、mB,验证动量守恒定律的表达式为(用图1中的字母表示)
;
解析 (3)要验证动量守恒定律,则mAv0=mAv1+mBv2,小球离开轨道后做平抛运动,抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以时间t得mAv0t=mAv1t+mBv2t,即mAOP=mAOM+mBON。
答案 (3)mAOP=mAOM+mBON
(4)某次实验中得出的落点情况如图2所示,假设碰撞过程中动量守恒,则入射小球质量mA和被碰小球质量mB之比为 。
解析 (4)如图2所示,代入上式得mA×22.50=mA×12.50+mB×35.00,解得mA:mB=7:2。
答案 (4)7:2
题型二 拓展与创新实验
【典例3】 某班物理兴趣小组选用如图所示的装置来“验证动量守恒定律”。将一段不可伸长的轻质绳一端与力传感器(可以实时记录绳所受的拉力)相连固定在O点,另一端连接小钢球A,把小钢球拉至M处可使绳水平拉紧。在小钢球最低点N右侧放置有一水平气垫导轨,气垫导轨上放有小滑块B(B上安装宽度较小且质量不计的遮光板)、光电门(已连接数字毫秒计),当地的重力加速度为g。
某同学按图所示安装气垫导轨、滑块B(调整滑块B的位置使小钢球自由下垂静止在N点时与滑块B接触而无压力)和光电门,调整好气垫导轨高度,确保小钢球A通过最低点时恰好与滑块B发生正碰。让小钢球A从某位置释放,摆到最低点N与滑块B碰撞,碰撞后小钢球A并没有反向,碰撞时间极短。
(1)为完成实验,除了毫秒计读数Δt、碰撞前瞬间绳的拉力F1、碰撞结束瞬间绳的拉力F2、滑块B质量mB和遮光板宽度d外,还需要测量的物理量有 。(用题中已给的物理量符号来表示)
A.小钢球A质量mA
B.绳长L
C.小钢球从M到N运动的时间
解析 (1)滑块B通过光电门时的瞬时速度vB=,根据牛顿第二定律得F1-mAg=mA,F2-mAg=mA,根据动量守恒定律得mAv1=mAv2+mBvB,整理得=+mB,所以还需要测量A的质量mA以及绳长L,故选A、B。
答案 (1)AB
(2)滑块B通过光电门时的瞬时速度vB= 。(用题中已给的物理量符号来表示)
解析 (2)滑块B通过光电门时的瞬时速度vB=。
答案 (2)
(3)实验中的动量守恒定律的表达式是 。(用题中已给的物理量符号来表示)
解析 (3)由(1)中分析可知,实验中的动量守恒定律的表达式是=+mB。
答案 (3)=+mB
如图所示,气垫导轨是常用的一种实验仪器。它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦。我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:
a.用天平分别测出滑块A、B的质量mA、mB;
b.调整气垫导轨,使导轨 ;
c.在滑块A、滑块B间放入一个被压缩的轻弹簧,用电动卡销锁定,静止放置在气垫导轨上;
d.用刻度尺测出滑块A的左端至挡板C的距离L1,B的右端至挡板D的距离L2;
e.按下电钮放开卡销,同时使分别记录滑块A、B运动时间的计时器开始工作,当滑块A、B分别碰撞挡板C、D时停止计时,记下滑块A、B分别到达挡板C、D的运动时间t1和t2。
(1)步骤b补充完整。
解析:(1)为保证A、B作用过程中系统动量守恒,应调整气垫导轨,使导轨水平。
答案:(1)水平
(2)利用上述测量的实验数据,验证动量守恒定律的表达式是 。
解析:(2)弹簧恢复原长后,A、B做匀速直线运动,A的速度大小为vA=,B的速度大小为vB=,以向左的方向为正方向,由动量守恒定律得mAvA-mBvB=0,由以上各式得mA-mB=0。
答案:(2)mA-mB=0
(3)利用上述实验数据还能测出被压缩弹簧的弹性势能的大小,其表达式是Ep= 。
解析:(3)由能量守恒定律得,被压缩弹簧的弹性势能Ep=mA+mB=mA+mB。
答案:(3)mA+mB
知能演练·提能力
NO.3
1.在用气垫导轨做“验证动量守恒定律”的实验时,
左侧滑块质量m1=200 g,右侧滑块质量m2=160 g,
挡光片宽度为3.00 cm,两滑块之间有一压缩的弹簧片,并用细线将两滑块连在一起,如图所示。开始时两滑块静止,烧断细线后,两滑块分别向左、右方向运动。挡光片通过光电门的时间分别为Δt1=0.30 s,Δt2=0.24 s。则烧断细线后两滑块的速度大小分别为v1'= m/s,v2'= m/s。烧断细线前两滑块动量之和为 kg·m/s,烧断细线后两滑块动量之和为 kg·m/s。可得到的结论是
。
解析:由平均速度公式可得v1'== m/s=0.1 m/s,v2'== m/s=0.125 m/s;因烧断细线之前,两滑块均静止,故烧断细线前两滑块动量之和为0;设向左为正方向,烧断细线后两滑块动量之和为0.2×0.1 kg·m/s+0.16×(-0.125)kg·m/s≈0;故烧断细线前后两滑块动量之和相等,烧断细线前、后,系统动量守恒。
答案:0.1 0.125 0 0 烧断细线前、后,系统动量守恒
2.“验证动量守恒定律”实验装置如图所示,让质量为m1的小球A从斜槽上的某一位置自由滚下,与静止在支柱上大小相等、质量为m2的小球B发生碰撞。(球A运动到水平槽末端时刚好与B球发生碰撞)
(1)安装轨道时,要求轨道末端 。
解析:(1)为了保证每次小球都做平抛运动,则需要轨道的末端水平。
答案:(1)水平
(2)两小球的质量应满足m1 (选填“>”“<”或“=”)m2。
解析:(2)验证碰撞中的动量守恒定律实验,为防止入射球反弹,入射球的质量应大于被碰球的质量,即m1>m2。
答案:(2)>
(3)用游标卡尺测量小球直径时的读数如图所示,则小球的直径d= cm。
解析:(3)游标卡尺读数为10 mm+4×0.1 mm=10.4 mm=1.04 cm。
答案:(3)1.04
(4)实验中还应测量的物理量是 。
A.两小球的质量m1和m2
B.小球A的初始高度h
C.轨道末端切线离地面的高度H
D.两小球平抛运动的时间t
E.球A单独滚下时的落地点P与O点的距离xOP
F.碰后A、B两小球的落地点M、N与O点的距离xOM和xON
解析:(4)小球离开轨道后做平抛运动,它们抛出点的高度相同,在空中的运动时间t相等,两球碰撞动量守恒,有m1v1=m1v1'+m2v2',
两边同时乘时间t,则m1v1t=m1v1't+m2v2't,
根据落点可化简为m1·xOP=m1·xOM+m2·(xON-d),则实验还需要测出:两小球的质量m1和m2,球A单独滚下时的落地点P点到O点的距离xOP和碰后A、B两小球的落地点M、N与O点的距离xOM和xON,故选A、E、F。
答案:(4)AEF
(5)若碰撞中动量守恒,根据图中各点间的距离,下列式子成立的是 。
A.= B.=
C.= D.=
解析:(5)根据动量守恒定律可得m1·xOP=m1·xOM+m2·,即==,故B正确。
答案:(5)B
3.如图甲所示,在做验证动量守恒定律实验时,在小车A的前端粘有橡皮泥,推动小车A使之做匀速运动,然后与原来静止在前方的小车B相碰并粘合成一体,继续做匀速运动。在小车A后连着纸带,电磁打点计时器的电源频率为50 Hz,长木板右端下面垫放小木片用以补偿阻力。
解析:(1)实验开始前需要补偿阻力,因为只有补偿阻力后,碰撞过程中系统所受的合外力为0,动量才守恒。补偿阻力的方法是长木板右端垫高,轻推小车A,当打出的纸带点迹均匀说明已补偿阻力。
答案:(1)需要 因为只有补偿阻力后,碰撞过程中系统所受的合外力为0,动量才守恒 长木板右端垫高,轻推小车A,当打出的纸带点迹均匀说明已补偿阻力
(1)实验开始前 (选填“需要”或“不需要”)补偿阻力,理由是 ,
方法是 。
(2)若打点纸带如图乙所示,并测得各计数点间距(已标在图上)。A为打下的第一点,则应选 段来计算A的碰前速度,应选 段来计算A和B碰后的共同速度。(以上两空选填“AB”“BC”“CD”或“DE”)
解析:(2)推动小车由静止开始运动,小车有个加速过程,在碰撞前做匀速直线运动,即在相同的时间内通过的位移相同,故BC段为匀速运动的阶段,故选BC段计算碰前的速度。碰撞过程是一个变速运动的过程,而A和B碰后共同运动时做匀速直线运动,故在相同的时间内通过相同的位移,故应选DE段来计算碰后共同的速度。
答案:(2)BC DE
(3)已测得小车A的质量m1=0.40 kg,小车B的质量m2=0.20 kg,由以上测量结果可得碰前总动量为 kg·m/s,碰后总动量为 kg·m/s。实验结论: 。(计算结果保留三位有效数字)
解析:(3)A碰前的速度v1== m/s=3.15 m/s,
碰后共同速度v2== m/s=2.085 m/s,
碰前总动量p1=m1v1=0.40×3.15 kg·m/s=1.26 kg·m/s
碰后的总动量p2=(m1+m2)v2=0.60×2.085 kg·m/s≈1.25 kg·m/s
说明在误差允许的范围内,碰撞前后总动量守恒。
答案:(3)1.26 1.25 在误差允许的范围内,碰撞前后总动量守恒
4.用如图所示装置来验证动量守恒定律,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,细线与竖直线之间夹角为α;A球由静止释放,摆到最低点时恰与B球发生正碰,碰撞后,A球摆到与竖直方向夹角为β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸,用来记录球B的落点,B球飞行的水平距离为x。
(1)用图中所示各个物理量的符号表示:碰撞前A球的速度vA= ;碰撞后B球的速度vB= ;
解析:(1)A球从静止释放到与B球碰撞的过程,根据动能定理,有
mAg(L-Lcosα)=mA
解得vA=
碰撞后B球做平抛运动,在竖直方向有H=gt2
在水平方向有x=vBt
联立解得vB=x。
答案:(1) x
(2)探究守恒量的表达式为 。
解析:(2)若A、B碰撞的过程中动量守恒有
mAvA=mAvA'+mBvB
从碰撞结束到A球摆到最高点,根据动能定理,有
-mAg(L-Lcos β)=-mAvA'2
解得vA'=
则探究守恒量的表达式为mA=mA+mBx。
答案:(2)mA=mA+mBx
三维达标·找不足
NO.4
1.(2022·浙江义乌高二期中)某同学用如图所示的装置“验证动量守恒定律”并测量处于压缩状态下的弹簧的弹性势能。实验前,用水平仪先将光滑操作台的台面调为水平。其实验步骤为:
A.用天平测出滑块A、B的质量mA、mB;
B.用细线将滑块A、B连接,使A、B间的弹簧处于压缩状态;
C.剪断细线,滑块A、B离开弹簧后均沿光滑操作台的台面运动,最后都滑离台面,记录A、B滑块的落地点M、N;
D.用刻度尺测出M、N距操作台边缘的水平距离x1、x2;
E.用刻度尺测出操作台面距地面的高度h。
请根据实验步骤完成下面填空:
(1)滑块A、B都离开桌面后,在空中运动的时间tA tB (选填“>”“<”或“=”);
解析:(1)滑块A、B都离开桌面后做平抛运动,竖直方向高度相同,由h=gt2知tA=tB=。
答案:(1)=
(2)如果滑块A、B组成的系统动量守恒,须满足的关系是 (用测量的物理量表示);
解析:(2)根据动量守恒定律有mAvA=mBvB
又tA=tB
可得mAx1=mBx2。
答案:(2)mAx1=mBx2
(3)剪断细线前,弹簧处于压缩状态下的弹性势能是 (用测量的物理量和重力加速度g表示)。
解析:(3)根据能量守恒定律得Ep=mA+mB
又vA=,vB=
联立解得Ep=。
答案:(3)
2.(2022·浙江杭十四中高二期中)用如图甲所示的装置研究碰撞中的动量守恒,小车P的前端、小车Q的后端均粘有橡皮泥,小车P的后端连接通过打点计时器的纸带,在长木板右端垫放木块以平衡摩擦力,推一下小车P,使之运动,与静止的小车Q相碰粘在一起,继续运动。
(1)实验获得的一条纸带如图乙所示,根据点迹的不同特征把纸带上的点进行了区域划分,用刻度尺测得B、C、D、E各点到起点A的距离。根据碰撞前后小车的运动情况,应选纸带上 段来计算小车P的碰撞前的速度。
解析:(1)小车P碰撞前做匀速直线运动,在相等时间内运动位移相等,由图乙所示纸带可知,应选择纸带上的BC段求出小车P碰撞前的速度。
答案:(1)BC
(2)测得小车P(含橡皮泥)的质量为m1,小车Q(含橡皮泥)的质量为m2,如果实验数据满足关系式 ,则说明小车P、Q组成的系统碰撞前后动量守恒。
解析:(2)设打点计时器打点时间间隔为T,由图乙所示的纸带可知,碰撞前小车的速度v=,碰撞后两小车的共同速度v'=,如果碰撞前后系统动量守恒,则m1v=(m1+m2)v',即m1=(m1+m2),整理得=。
答案:(2)=
(3)如果在测量小车P的质量时,忘记粘橡皮泥,则所测系统碰撞前总动量与系统碰撞后总动量相比,将 (选填“偏大”“偏小”或“相等”)。
解析:(3)如果在测量小车P的质量时,忘记粘橡皮泥,则小车P质量的测量值小于真实值,由(2)中表达式可知,所测系统碰撞前总动量小于碰撞后系统的总动量。
答案:(3)偏小
3.(2022·浙江宁波高二期末)某物理兴趣小组利用如图甲所示的装置进行“验证动量守恒定律”的实验。在足够大的水平平台上的A点放置一个光电门,水平平台上A点右侧摩擦很小,可忽略不计,左侧为粗糙水平面。实验步骤如下:
A.在小滑块a上固定一个宽度为d的窄挡光片;
B.用天平分别测出小滑块a(含挡光片)和小球b的质量ma、mb;
C.a和b用细线连接,中间夹一被压缩了的水平轻质短弹簧,静止放置在平台上;
D.烧断细线后,a、b瞬间被弹开,并向相反方向运动;
E.记录滑块a通过光电门时挡光片的遮光时间t;
F.小球b从平台边缘飞出后,落在水平地面的B点,用刻度尺测出平台距水平地面的高度h及平台边缘重垂线与B点之间的水平距离xb;
G.改变弹簧压缩量,进行多次测量。
(1)用螺旋测微器测量挡光片的宽度,如图乙所示,则挡光片的宽度为 mm。
解析:(1)螺旋测微器的固定刻度读数为2.5 mm,可动刻度读数为5.0×0.01 mm=0.050 mm,所以最终读数为2.5 mm+0.050 mm=2.550 mm。
答案:(1)2.550
(2)该实验要验证动量守恒定律,则只需验证两物体a、b弹开后的动量大小相等,即 = 。(用上述实验所涉及物理量的字母表示,当地重力加速度为g)
解析:(2)烧断细线后,a向左运动,经过光电门,根据速度公式可知,a经过光电门的速度为va=,故a的动量大小为pa=ma。b离开平台后做平抛运动,根据平抛运动规律可得h=gt2,xb=vbt,解得vb=xb,b的动量大小为pb=mbxb,若动量守恒,设向右为正,则有0=mbvb-mava,即ma=mbxb。
答案:(2) mbxb
4.在“验证动量守恒定律”实验中,实验装置如图所示,按照以下步骤进行操作:
①在平木板表面钉上白纸和复写纸,并将该木板竖直立于紧靠槽口处,将小球a从斜槽轨道上固定点处由静止释放,撞到木板并在白纸上留下痕迹O;
②将木板水平向右移动一定距离并固定,再将小球a从固定点处由静止释放,撞到木板上得到痕迹B;
③把小球b静止放在斜槽轨道水平段的最右端,让小球a仍从固定点处由静止释放,和小球b相碰后,两球撞在木板上得到痕迹A和C。
(1)下列措施可减小实验误差的是 。
A.斜槽轨道必须是光滑的
B.每次实验均重复几次后,再记录平均落点
C.a球和b球的半径和质量满足ra=rb和ma<mb
解析:(1)本实验是“验证动量守恒定律”的,所以实验误差与斜槽轨道的光滑程度无关,A错误;每次实验均重复几次后,再记录平均落点,这样可减小实验误差,B正确;要产生正碰,a球和b球的半径需满足ra=rb,为防止两球碰撞后a球反弹,质量要满足ma>mb,C错误。
答案:(1)B
(2)为完成本实验,必须测量的物理量有 。
A.a球开始释放的高度h
B.木板水平向右移动的距离L
C.a球和b球的质量ma、mb
D.O点到A、B、C三点的距离y1、y2、y3
解析:(2)每次a球释放的高度h确定不变就可以,不用测量h值,A错误;因为小球每次打在木板上时,水平方向的位移相等,所以不需测量木板水平向右移动的距离L,B错误;要验证动量守恒定律,必须测量a球和b球的质量ma、mb,C正确;需要计算小球运动的时间,则要测量O点到A、B、C三点的距离y1、y2、y3,D正确。
答案:(2)CD
(3)只要验证等式 成立,即表示碰撞中动量守恒。[用(2)中测量的物理量表示]
解析:(3)a、b两球碰撞后做平抛运动,由L=vt和y=gt2,可得v=
则由动量守恒定律可得mav0=mav1+mbv2
即ma=ma+mb
整理得=+
若表达式=+成立,即表示碰撞中动量守恒。
答案:(3)=+
5.如图所示,用“碰撞实验器”可以验证动量守恒定律,实验时先让入射小球从特殊材料制成的光滑轨道上某一固定位置S由静止开始滚下,从轨道末端O点水平抛出,落到与轨道O点连接的斜面上,记下小球与斜面第一次碰撞留下的落点痕迹。再把被碰小球放在斜槽轨道末端,让入射小球仍从位置S由静止滚下,与被碰小球碰撞后都落到斜面上,记下两小球与斜面第一次碰撞留下的落点痕迹。每组实验都是从O点沿斜面向下依次标记M、P、N为三个落点的位置(不考虑小球在斜面上的多次碰撞,小球可视作质点),O点与各落点的距离为LOM、LOP、LON,入射小球A的质量是被碰小球B的质量的4倍。[第(2)(3)问均用LOM、LOP、LON表示]
解析:(1)若动量守恒则满足4mv0=4mv1+mv2,因为小球离开斜槽做平抛运动时,由tan θ=,可得小球在斜面上的位移x==v2∝v2,所以v∝,可得4=4+,若该碰撞是弹性碰撞,还应满足的关系式为×4m=×4m+m,可得4LOP=4LOM+LON。
答案:(1)4=4+ 4LOP=4LOM+LON
(1)第一组同学选择A球为入射球,B为被碰球,若满足关系式 ,则可以认为两球碰撞前后总动量守恒。若该碰撞是弹性碰撞,还应满足的关系式为 。
(2)第二组同学选择B球为入射球,A为被碰球,若该碰撞是弹性碰撞,则能说明两球碰撞前后总动量守恒的关系式为 。
解析:(2)若选择B球为入射球,A为被碰球,若发生弹性碰撞,则mv0=mv1'+4mv2',m=mv1'2+·4mv2'2,解得v1'=-0.6v0,v2'=0.4v0,即入射球B应该反向弹回到斜槽上后向下运动再做平抛落在斜面上,因B做平抛的速度较A大,可知B将落在N点,A将落在M点,此时动量守恒表达式应该为m=-m+4m,即4=+。
答案:(2)4=+
6.某实验小组利用如图所示的实验装置验证动量守恒定律。实验的主要步骤如下:
①用游标卡尺测量小球A、B的直径d,用毫米刻度尺测量细线的长度L,用天平测量小球A、B的质量分别为m1、m2;
②用两条细线分别将球A、B悬挂于同一水平高度,且自然下垂时两球恰好相切,球心位于同一水平线上;
③将球A向左拉起使其细线与竖直方向的夹角为α时由静止释放,与球B碰撞后,测得球A向左摆到最高点时其细线与竖直方向的夹角为θ1,球B向右摆到最高点时其细线与竖直方向的夹角为θ2。
回答下列问题:
(1)在实验步骤中,有多余操作过程的步骤是 ;
解析:(1)小球碰撞后由动能定理得
mg(L-Lcos θ)=mv2
解得v=
由动量守恒定律表达式可知细线的长度可以约掉,所以不必测量,故有多余操作的步骤是①;
答案:(1)①
(2)为保证A碰撞后向左摆动,则A、B两球质量应满足m1 m2(填“>”“<”或“=”);
解析:(2)为使A球碰撞后能反弹,则A、B两球质量应满足m1<m2;
答案:(2)<
(3)若两球碰撞前后动量守恒,则= (用③中测量的量表示);
解析:(3)小球A下摆过程中只有重力做功,机械能守恒,由机械能守恒定律得
m1=m1gL(1-cos α)
碰撞后,对A、B两小球摆动过程中只有重力作用,机械能守恒,对A有m1v1'2=m1gL(1-cos θ1)
对B有m2=m2gL(1-cos θ2)
若两球碰撞过程系统动量守恒,以水平向右为正方向,由动量守恒定律得
m1v1=-m1v1'+m2v2
解得m1=-m1+m2
则=;
答案:(3)
(4)若两球的碰撞为弹性碰撞,并且碰撞之后两个小球摆到最高点时其细线与竖直方向的夹角θ1=θ2,则= ,并且cos θ1=cos θ2= (用α表示)。
解析:(4)若是弹性碰撞,则还满足机械能守恒定律,由动量守恒定律和机械能守恒定律得
m1v1=-m1v1'+m2v2
m1=m1v1'2+m2
又θ1=θ2
联立解得=,cos θ1=cos θ2=。
答案:(4)
感谢您的耐心观看
