人教版(2019)选择性必修第一册 1.5 弹性碰撞和非弹性碰撞 课件(共28张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修第一册 1.5 弹性碰撞和非弹性碰撞 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 08:11:18 | ||
图片预览






文档简介
(共28张PPT)
动量守恒定律
第5节 弹性碰撞和非弹性碰撞
CONTENTS
01
碰撞的分类
02
弹性碰撞
03
碰撞三原则
04
典型例题
目录
碰撞模型的建构
陨石撞地球
球拍打网球
汽车的碰撞
微观的原子
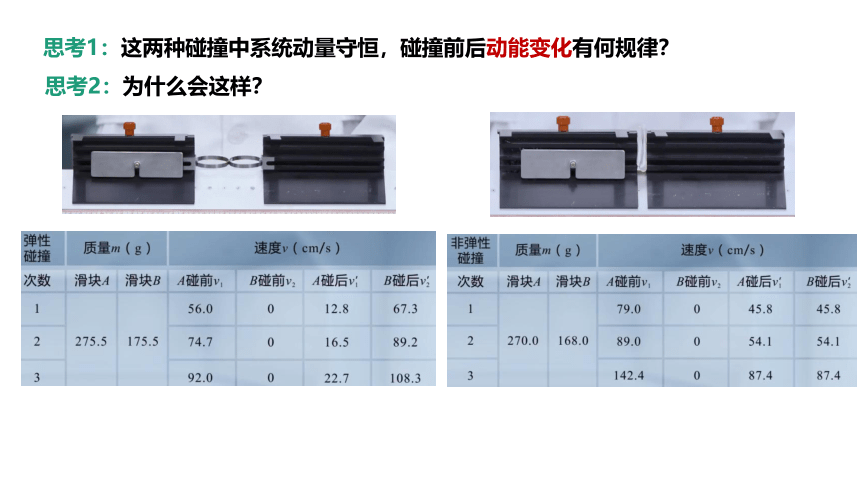
思考1:这两种碰撞中系统动量守恒,碰撞前后动能变化有何规律?
思考2:为什么会这样?
思考2:对比这两种碰撞有何不同
弹性碰撞
非弹性碰撞
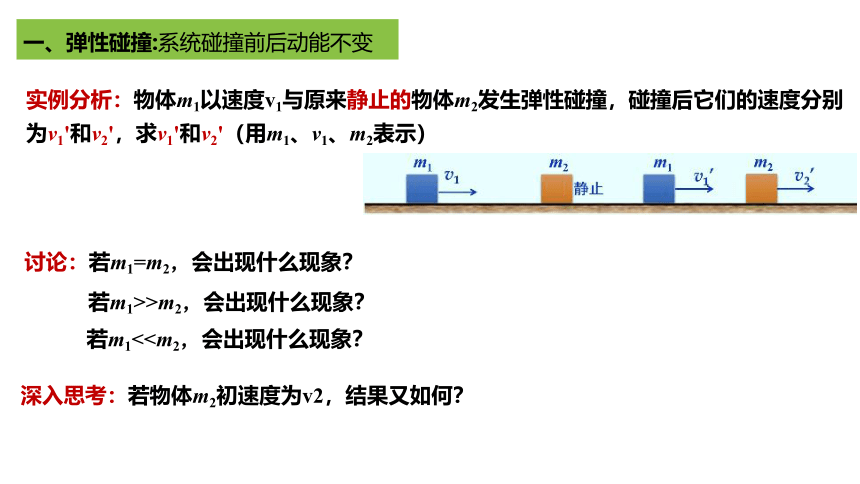
一、弹性碰撞:系统碰撞前后动能不变
实例分析:物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1'和v2',求v1'和v2'(用m1、v1、m2表示)
讨论:若m1=m2,会出现什么现象?
若m1>>m2,会出现什么现象?
若m1<深入思考:若物体m2初速度为v2,结果又如何?
v1
m1
m2
碰前:m1速度v1,m2静止
碰后:m1速度v'1,m2速度v'2
动量守恒:
机械能守恒:
解得:
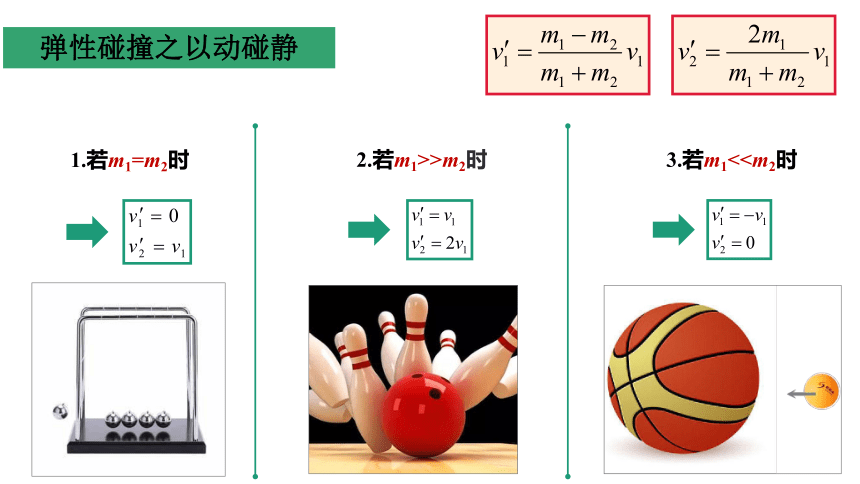
弹性碰撞之以动碰静
规律
1.若m1=m2时
2.若m1>>m2时
3.若m1<弹性碰撞之以动碰静
二、非弹性碰撞:系统碰撞前后动能减小
实例分析:物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们以相同的速度v共运动,求v共,动能有损失吗?若有,损失了多少?(用m1、v1、m2表示)
v共
完全非弹性碰撞
v1
m1
m2
一、按碰撞前后能量变化分类
1.弹性碰撞:
2.非弹性碰撞:
(完全非弹性碰撞:
动量守恒,机械能守恒
动量守恒,机械能不守恒
动量守恒,机械能损失最大)
1.质量为m、速度为v的A球跟质量为3m的静止B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度可能有不同的值.请你论证:碰后B球的速度可能是以下值吗?
(1)0.6v;(2)0.4v;(3)0.2v
若A、B弹性碰撞,根据动量守恒定律和机械能守恒定律得B获得的最大速度为
解:
若A、B完全非弹性碰撞,根据动量守恒定律,B获得的最小速度为
弹 性 碰 撞
完全非弹性碰撞
实验室的碰撞模拟:
应用:动量能量混合专题:子弹大木块类问题
一质量为M的木块放在光滑的水平面上,一质量m的子弹以初速度v0水平飞来打进木块并留在其中,设子弹与木块之间相互作用力为Ff,则
(1)子弹、木块相对静止时的速度是多少?
(2)子弹在木块内运动的时间有多长?
(3)子弹、木块发生的位移s1、s2以及子弹打进木块的深度s
(4)系统损失的机械能、系统增加的内能分别是多少?
专题 以动碰动模型的应用
一、弹性碰撞:系统碰撞前后动能不变
实例分析:物体m1以速度v1与速度为v2的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1'和v2',求v1'和v2'(用m1、v1、m2表示)
v2
已知:篮球的质量为500g,乒乓球的质量为2.5g,篮球刚开始下落时,底部距离地面的高度为0.8m,篮球直径为0.25m。不计碰撞过程中的能量损失,不计空气阻力,估算乒乓球碰后所能到达的最大高度。
专题 碰撞中的实际问题
学以致用之碰撞问题的可能性判断
例题1.两个小球A、B在光滑水平面上相向运动,已知它们的质量分别是m1=4 kg,m2=2 kg,A的速度v1=3 m/s(设为正),B的速度v2=-3 m/s,则它们发生正碰后,其速度可能分别是( )
A.均为+1.5 m/s B.+4 m/s和-5 m/s
C.+2 m/s和-1 m/s D.-1 m/s和+5 m/s
D
动量不守恒
能量不守恒
速度不符合
例题2.质量为M的物块以速度v运动,与质量为m的静止物块发生正碰,碰撞后两者的动量正好相等,两者质量之比M : m不可能为( )
A.2 B.2.5 C.3 D.3.5
学以致用之碰撞问题的可能性判断
解:假设碰后二者的动量都为 p:
① 动量守恒定律:碰撞过程中系统的总动量为2p.
② 机械能不增加:
③ 速度符合实际:
D
学以致用之碰撞问题的可能性判断
例题3.小球1追碰小球2.碰撞前两球的动量分别为p1=5 kg·m/s.
p2=7 kg·m/s.正碰后小球2的动量p2′=10 kg·m/s.则两球的质量关系可能是( )
A.m2=m1 B.m2=2m1
C.m2=4m1 D.m2=6m1
C
动量守恒定律:
机械能不增加:
v2′
碰撞三原则
碰撞三原则
1.碰前同向运动,则v1>v2,
否则无法实现碰撞.
①.碰后同向,则 ,
且
②.碰后反向,则
且
2.碰前相向运动,至少有一个物体速度方向改变
方法提炼:排除法
速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
课堂练习2
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
有些核反应堆里要让中子与原子核正碰,以便把中子的速率降下来.为此应该选用质量较大的还是质量较小的原子核?为什么?
课堂练习3
解:将上述碰撞视为弹性碰撞,设中子:质量m1,碰前v,方向为正,碰后速度v ;原子核:质量m2,碰前静止
中子质量一般小于原子核的质量,因此:
m2越小,v 越小,故选择质量较小的原子核来降低中子的速度。核电站常用石墨或重水作为中子减速剂。
专题 习题中的典型问题:分步法
1.如图所示,将一个质量为1.99kg的砂箱,用长为0.5m的轻绳悬挂在光滑的圆环上,圆环套在一个光滑的固定杆上,圆环质量为1kg,一颗质量为10g的子弹水平射入砂箱,砂箱发生摆动,若子弹射击砂箱时的速度为600m/s,求:
(1)子弹刚打入砂箱时,它们共同速度的大小;
(2)子弹刚打入砂箱时,砂箱对细绳作用力的大小;
(3)子弹与砂箱共同上摆过程中,摆过的最大角度的余弦值。
再见
动量守恒定律
第5节 弹性碰撞和非弹性碰撞
CONTENTS
01
碰撞的分类
02
弹性碰撞
03
碰撞三原则
04
典型例题
目录
碰撞模型的建构
陨石撞地球
球拍打网球
汽车的碰撞
微观的原子
思考1:这两种碰撞中系统动量守恒,碰撞前后动能变化有何规律?
思考2:为什么会这样?
思考2:对比这两种碰撞有何不同
弹性碰撞
非弹性碰撞
一、弹性碰撞:系统碰撞前后动能不变
实例分析:物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1'和v2',求v1'和v2'(用m1、v1、m2表示)
讨论:若m1=m2,会出现什么现象?
若m1>>m2,会出现什么现象?
若m1<
v1
m1
m2
碰前:m1速度v1,m2静止
碰后:m1速度v'1,m2速度v'2
动量守恒:
机械能守恒:
解得:
弹性碰撞之以动碰静
规律
1.若m1=m2时
2.若m1>>m2时
3.若m1<
二、非弹性碰撞:系统碰撞前后动能减小
实例分析:物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们以相同的速度v共运动,求v共,动能有损失吗?若有,损失了多少?(用m1、v1、m2表示)
v共
完全非弹性碰撞
v1
m1
m2
一、按碰撞前后能量变化分类
1.弹性碰撞:
2.非弹性碰撞:
(完全非弹性碰撞:
动量守恒,机械能守恒
动量守恒,机械能不守恒
动量守恒,机械能损失最大)
1.质量为m、速度为v的A球跟质量为3m的静止B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B球的速度可能有不同的值.请你论证:碰后B球的速度可能是以下值吗?
(1)0.6v;(2)0.4v;(3)0.2v
若A、B弹性碰撞,根据动量守恒定律和机械能守恒定律得B获得的最大速度为
解:
若A、B完全非弹性碰撞,根据动量守恒定律,B获得的最小速度为
弹 性 碰 撞
完全非弹性碰撞
实验室的碰撞模拟:
应用:动量能量混合专题:子弹大木块类问题
一质量为M的木块放在光滑的水平面上,一质量m的子弹以初速度v0水平飞来打进木块并留在其中,设子弹与木块之间相互作用力为Ff,则
(1)子弹、木块相对静止时的速度是多少?
(2)子弹在木块内运动的时间有多长?
(3)子弹、木块发生的位移s1、s2以及子弹打进木块的深度s
(4)系统损失的机械能、系统增加的内能分别是多少?
专题 以动碰动模型的应用
一、弹性碰撞:系统碰撞前后动能不变
实例分析:物体m1以速度v1与速度为v2的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1'和v2',求v1'和v2'(用m1、v1、m2表示)
v2
已知:篮球的质量为500g,乒乓球的质量为2.5g,篮球刚开始下落时,底部距离地面的高度为0.8m,篮球直径为0.25m。不计碰撞过程中的能量损失,不计空气阻力,估算乒乓球碰后所能到达的最大高度。
专题 碰撞中的实际问题
学以致用之碰撞问题的可能性判断
例题1.两个小球A、B在光滑水平面上相向运动,已知它们的质量分别是m1=4 kg,m2=2 kg,A的速度v1=3 m/s(设为正),B的速度v2=-3 m/s,则它们发生正碰后,其速度可能分别是( )
A.均为+1.5 m/s B.+4 m/s和-5 m/s
C.+2 m/s和-1 m/s D.-1 m/s和+5 m/s
D
动量不守恒
能量不守恒
速度不符合
例题2.质量为M的物块以速度v运动,与质量为m的静止物块发生正碰,碰撞后两者的动量正好相等,两者质量之比M : m不可能为( )
A.2 B.2.5 C.3 D.3.5
学以致用之碰撞问题的可能性判断
解:假设碰后二者的动量都为 p:
① 动量守恒定律:碰撞过程中系统的总动量为2p.
② 机械能不增加:
③ 速度符合实际:
D
学以致用之碰撞问题的可能性判断
例题3.小球1追碰小球2.碰撞前两球的动量分别为p1=5 kg·m/s.
p2=7 kg·m/s.正碰后小球2的动量p2′=10 kg·m/s.则两球的质量关系可能是( )
A.m2=m1 B.m2=2m1
C.m2=4m1 D.m2=6m1
C
动量守恒定律:
机械能不增加:
v2′
碰撞三原则
碰撞三原则
1.碰前同向运动,则v1>v2,
否则无法实现碰撞.
①.碰后同向,则 ,
且
②.碰后反向,则
且
2.碰前相向运动,至少有一个物体速度方向改变
方法提炼:排除法
速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
课堂练习2
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
有些核反应堆里要让中子与原子核正碰,以便把中子的速率降下来.为此应该选用质量较大的还是质量较小的原子核?为什么?
课堂练习3
解:将上述碰撞视为弹性碰撞,设中子:质量m1,碰前v,方向为正,碰后速度v ;原子核:质量m2,碰前静止
中子质量一般小于原子核的质量,因此:
m2越小,v 越小,故选择质量较小的原子核来降低中子的速度。核电站常用石墨或重水作为中子减速剂。
专题 习题中的典型问题:分步法
1.如图所示,将一个质量为1.99kg的砂箱,用长为0.5m的轻绳悬挂在光滑的圆环上,圆环套在一个光滑的固定杆上,圆环质量为1kg,一颗质量为10g的子弹水平射入砂箱,砂箱发生摆动,若子弹射击砂箱时的速度为600m/s,求:
(1)子弹刚打入砂箱时,它们共同速度的大小;
(2)子弹刚打入砂箱时,砂箱对细绳作用力的大小;
(3)子弹与砂箱共同上摆过程中,摆过的最大角度的余弦值。
再见
