北师大版八年级数学上册试题 第7章 平行线的证明 (单元培优卷)(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 第7章 平行线的证明 (单元培优卷)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 647.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-24 09:12:53 | ||
图片预览



文档简介
第7章《平行线的证明》(单元培优卷)
一、单选题(本大题共10小题,每小题3分,共30分)
1.甲、乙、丙、丁4人进行乒乓球单循环比赛(每两个人都要比赛一场),结果甲胜了丁,并且甲、乙、丙胜的场数相同,则丁胜的场数是( )
A.3 B.2 C.1 D.0
2.过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )
A. B.
C. D.
3.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
A.先向左转130°,再向左转50° B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40° D.先向左转50°,再向左转40°
4.若一个三角形三个内角度数的比为2︰7︰4,那么这个三角形是
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
5.如图,直线,直线,若,则( )
A. B. C. D.
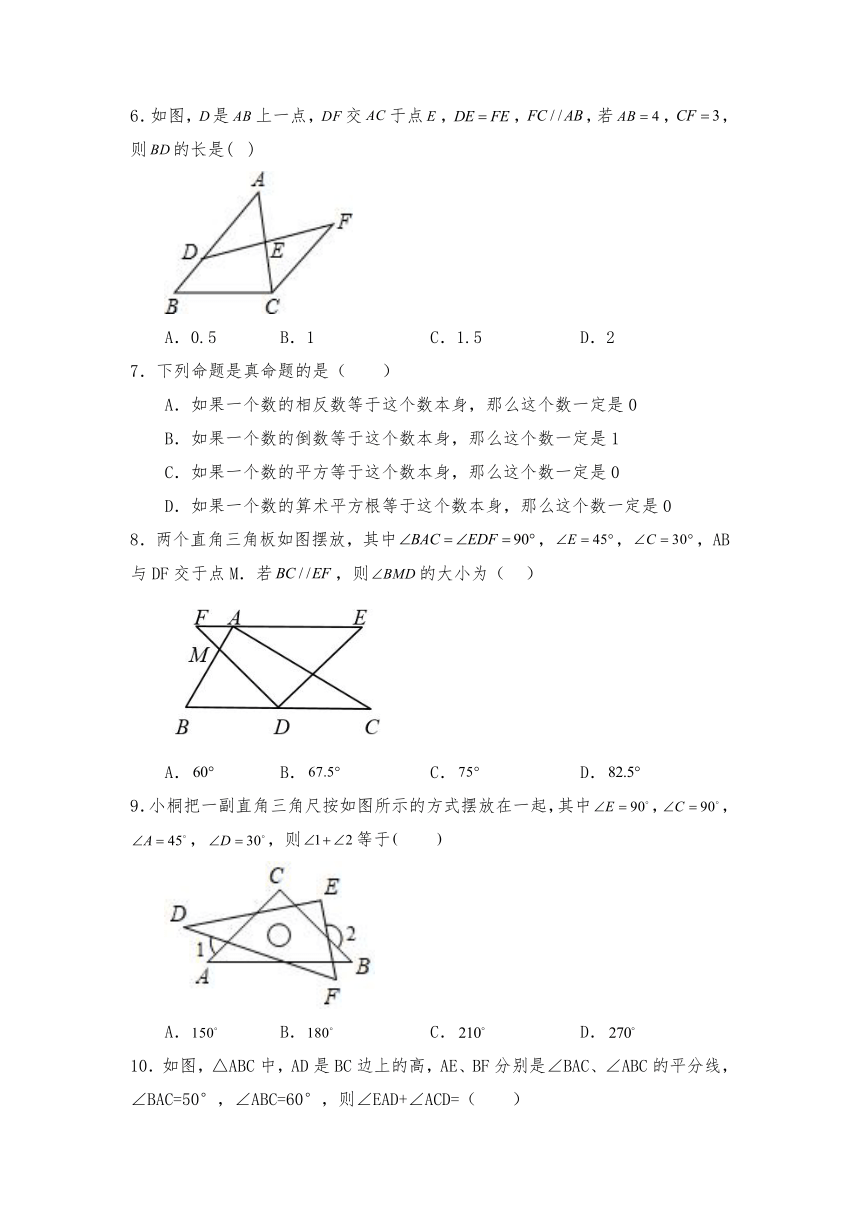
6.如图,是上一点,交于点,,,若,,则的长是( )
A.0.5 B.1 C.1.5 D.2
7.下列命题是真命题的是( )
A.如果一个数的相反数等于这个数本身,那么这个数一定是0
B.如果一个数的倒数等于这个数本身,那么这个数一定是1
C.如果一个数的平方等于这个数本身,那么这个数一定是0
D.如果一个数的算术平方根等于这个数本身,那么这个数一定是0
8.两个直角三角板如图摆放,其中,,,AB与DF交于点M.若,则的大小为( )
A. B. C. D.
9.小桐把一副直角三角尺按如图所示的方式摆放在一起,其中,,,,则等于
A. B. C. D.
10.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
二、填空题(本大题共8小题,每小题4分,共32分)
11.将命题“同角的补角相等”改写成“如果……,那么……”的形式为_________________.
12.为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是_____.
13.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为__________.(任意添加一个符合题意的条件即可)
14.如图,
,DE过点C,且DE//AB,若,
则∠A=_____,∠B=______.
15.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=_________.
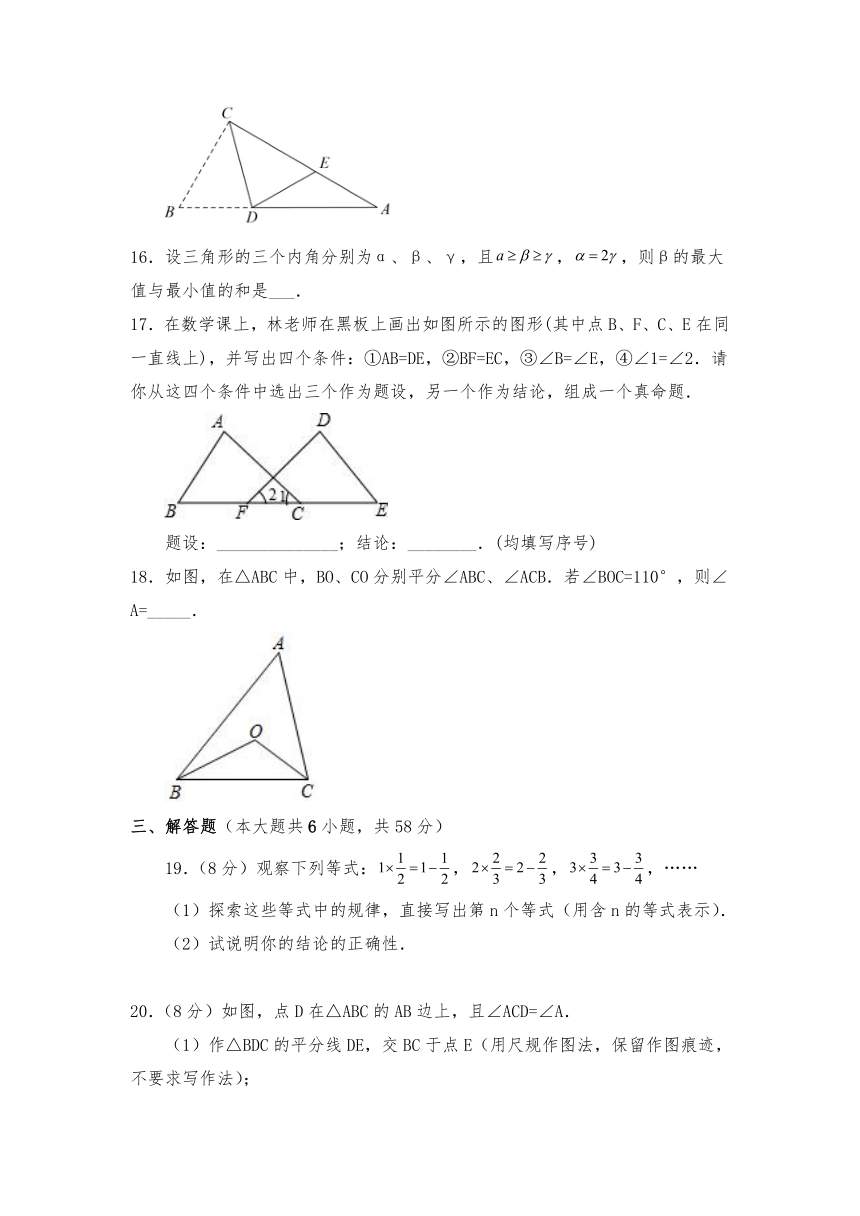
16.设三角形的三个内角分别为α、β、γ,且,,则β的最大值与最小值的和是___.
17.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
题设:______________;结论:________.(均填写序号)
18.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
三、解答题(本大题共6小题,共58分)
19.(8分)观察下列等式:,,,……
(1)探索这些等式中的规律,直接写出第n个等式(用含n的等式表示).
(2)试说明你的结论的正确性.
20.(8分)如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作△BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
21.(10分)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.
22.(10分)如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
23.(10分)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示).
(2)用等式表示线段MB与 PQ之间的数量关系,并证明.
24.(12分)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在中,,,边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图1):
(1)延长到Q使得;(2)再连接,把集中在中;(3)利用三角形的三边关系可得的取值范围,进而求出的取值范围.
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
求出的取值范围.
求如图中与的位置关系并证明;
思考:已知,如图,是的中线,,,,试探究线段与的关系,并证明.
参考答案
一、单选题
1.D
解:四个人共有6场比赛,由于甲、乙、丙三人胜的场数相同,所以只有两种可能性:甲胜1场或甲胜2场;由此进行分析即可.
详解:四个人共有6场比赛,由于甲、乙、丙三人胜的场数相同,
所以只有两种可能性:甲胜1场或甲胜2场;
若甲只胜一场,这时乙、丙各胜一场,说明丁胜三场,这与甲胜丁矛盾,
所以甲只能是胜两场,
即:甲、乙、丙各胜2场,此时丁三场全败,也就是胜0场.
答:甲、乙、丙各胜2场,此时丁三场全败,丁胜0场.
故选D.
2.D
【分析】根据平行线的判定方法一一判断即可.
解:A、由作图可知,内错角相等两直线平行,本选项不符合题意.
B、由作图可知,同位角相等两直线平行,本选项不符合题意.
C、与作图可知,垂直于同一条直线的两条直线平行,本选项不符合题意,
D、无法判断两直线平行,
故选:D.
3.B
解:根据同位角相等,两直线平行,可得B.
4.C
解:设三角形的三个内角分别为:2x,7x,4x.
∵三角形三个内角度数的比为2:7:4,
∴2x+7x+4x=180°,
∴7x≈97°,
∴这个三角形是钝角三角形.故选C
5.C
【分析】根据垂直的定义和余角的定义列式计算得到,根据两直线平行,同位角相等可得.
解:如图,
直线,
.
,
,
直线,
,
故选C.
6.B
【分析】根据平行线的性质,得出,,根据全等三角形的判定,得出,根据全等三角形的性质,得出,根据,,即可求线段的长.
解:∵,
∴,,
在和中,
∴,
∴,
∵,
∴.
故选B.
7.A
【分析】根据相反数是它本身的数为0;倒数等于这个数本身是±1;平方等于它本身的数为1和0;算术平方根等于本身的数为1和0进行分析即可.
解:A、如果一个数的相反数等于这个数本身,那么这个数一定是0,是真命题;
B、如果一个数的倒数等于这个数本身,那么这个数一定是1,是假命题;
C、如果一个数的平方等于这个数本身,那么这个数一定是0,是假命题;
D、如果一个数的算术平方根等于这个数本身,那么这个数一定是0,是假命题;
故选A.
8.C
【分析】根据,可得再根据三角形内角和即可得出答案.
解:由图可得
∵,
∴
∴
故选:C.
9.C
【分析】根据三角形的内角和定理和三角形外角性质进行解答即可.
解:如图:
,,
,,
∴
=
=,
故选C.
10.A
【分析】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,可得∠EAD+∠ACD=75°.
解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°,
故选:A.
二、填空题
11.如果两个角是同一个角的补角,那么这两个角相等.
【分析】每一个命题都是基于条件的一个判断,只要把条件部分和判断部分分开即可.
解:如果两个角是同一个角的补角,那么这两个角相等,
故答案为:如果两个角是同一个角的补角,那么这两个角相等.
12.1024
解:分析:根据题意可得每次挑选都是去掉偶数,进而得出需要挑选的总次数进而得出答案.
详解:∵将这些金蛋按1﹣2018的顺序进行标号,第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,
∴剩余的数字都是偶数,是2的倍数,;
∵他将剩下的金蛋在原来的位置上又按1﹣1009编了号,
又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋,
∴剩余的数字为4的倍数,
以此类推:2018→1009→504→252→126→63→31→15→7→3→1
共经历10次重新编号,故最后剩余的数字为:210=1024.
故答案为1024.
13.∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE
【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断(答案不唯一).
解:若,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
14. 50° 40°
解:∵DE∥AB,∠ACD=50°,
∴∠A=∠ACD=50°,
∵∠ACB=90°,
∴∠B=90°-∠A=90°-50°=40°.
15.71°
解:∵在Rt△ABC中,∠ACB=90°,∠A=26°,
∴∠B=64°,
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠CED=∠B=64°,
∴∠CDE=180°﹣∠ECD﹣∠CED=71°,
故答案为71°.
16.117°
【分析】根据三角形的三个内角和为180°,以及α=2γ,可得出β与γ的关系式,再根据α≥β≥γ,得出α≥180°-3γ≥γ,从而求出γ的取值范围.
解:∵α+β+γ=180°,
∴β=180°-α-γ=180°-3γ,
所以α≥180°-3γ≥γ,
∴5γ≥180°≥4γ,
45°≥γ≥36°,
所以72°≥β≥45°,
∴β的最大值与最小值的和=72°+45°=117°,
故答案为117°.
17. ①②③ ④
解:解题设:①②③;结论:④.
证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF.
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),∴∠1=∠2.
此题可以分成三种情况:
情况一:题设:①②③;结论:④,可以利用SAS定理证明△ABC≌△DEF.
情况二:题设:①③④;结论:②,可以利用AAS证明△ABC≌△DEF:
在△ABC和△DEF中,∵ AB=DE,∠B=∠E,∠1=∠2,∴△ABC≌△DEF(AAS).
∴BC=EF,∴BC-FC=EF-FC,即BF=EC.
情况三:题设:②③④;结论:①,可以利用ASA证明△ABC≌△DEF,再根据全等三角形的
性质可推出结论:
∵BF=EC,∴BF+CF=EC+CF,即BC=EF.
在△ABC和△DEF中,∵∠B=∠E ,BC=EF,∠1=∠2,∴△ABC≌△DEF(ASA).∴AB=DE.
18.40°
【分析】先根据角平分线的定义得到∠OBC=∠ABC,∠OCB=∠ACB,再根据三角形内角和定理得∠BOC+∠OBC+∠OCB=180°,则∠BOC=180°﹣(∠ABC+∠ACB),由于∠ABC+∠ACB=180°﹣∠A,所以∠BOC=90°+∠A,然后把∠BOC=110°代入计算可得到∠A的度数.
解:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣(180°﹣∠A)=90°+∠A,
而∠BOC=110°,
∴90°+∠A=110°
∴∠A=40°.
故答案为40°.
三、解答题
19.
解:(1)猜想:;
(2)证:右边===左边,即
20.
解:(1)如图所示:
(2)DE∥AC
∵DE平分∠BDC,
∴∠BDE=∠BDC,
∵∠ACD=∠A,∠ACD+∠A=∠BDC,
∴∠A=∠BDC,
∴∠A=∠BDE,
∴DE∥AC.
21.
解:证明:∵AF=DC,
∴AC+FC=FC+DF,
∴AC=DF,
又∵AB=DE,∠A=∠D,
∴△ACB≌△DEF(SAS),
∴∠ACB=∠DFE,
∴BC∥EF.
22.
解:(1)证明:∵BF=EC,
∴BF+CF=CF+CE,
∴BC=EF
∵AB=DE,AC=DF
∴△ABC≌△DEF(SSS)
(2)AB∥DE,AC∥DF,理由如下,
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.
23.
解:(1) ∠AMQ=45°+α.理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠PAB=45°-α,∠AHM=90°,
∴∠AMQ=180°-∠AHM-∠PAM=45°+α;
(2)线段MB与PQ之间的数量关系:PQ=MB.
理由如下:
连接AQ,过点M作ME⊥QB,
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=α+45°=∠AMQ,
∴AP=AQ=QM,
在Rt△APC和Rt△QME中,
∴Rt△APC≌Rt△QME,
∴PC=ME,
∴△MEB是等腰直角三角形,
∴,
∴PQ=MB.
24.
(1)解:∵是的中线,
∴,
在和中,
,
∴,
∴,
在中,,
∴,
∴,
故答案为;
(2)解:,理由:由(1)知,,
∴,
∴;
(3)解:,,
理由:如图2,延长到Q使得,连接,
由(1)知,,
∴,
∵,
∴,
在中,,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
延长交于P,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
即:.
一、单选题(本大题共10小题,每小题3分,共30分)
1.甲、乙、丙、丁4人进行乒乓球单循环比赛(每两个人都要比赛一场),结果甲胜了丁,并且甲、乙、丙胜的场数相同,则丁胜的场数是( )
A.3 B.2 C.1 D.0
2.过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )
A. B.
C. D.
3.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向平行行驶,那么这两个拐弯的角度可能是( )
A.先向左转130°,再向左转50° B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40° D.先向左转50°,再向左转40°
4.若一个三角形三个内角度数的比为2︰7︰4,那么这个三角形是
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
5.如图,直线,直线,若,则( )
A. B. C. D.
6.如图,是上一点,交于点,,,若,,则的长是( )
A.0.5 B.1 C.1.5 D.2
7.下列命题是真命题的是( )
A.如果一个数的相反数等于这个数本身,那么这个数一定是0
B.如果一个数的倒数等于这个数本身,那么这个数一定是1
C.如果一个数的平方等于这个数本身,那么这个数一定是0
D.如果一个数的算术平方根等于这个数本身,那么这个数一定是0
8.两个直角三角板如图摆放,其中,,,AB与DF交于点M.若,则的大小为( )
A. B. C. D.
9.小桐把一副直角三角尺按如图所示的方式摆放在一起,其中,,,,则等于
A. B. C. D.
10.如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
二、填空题(本大题共8小题,每小题4分,共32分)
11.将命题“同角的补角相等”改写成“如果……,那么……”的形式为_________________.
12.为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是_____.
13.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为__________.(任意添加一个符合题意的条件即可)
14.如图,
,DE过点C,且DE//AB,若,
则∠A=_____,∠B=______.
15.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=_________.
16.设三角形的三个内角分别为α、β、γ,且,,则β的最大值与最小值的和是___.
17.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
题设:______________;结论:________.(均填写序号)
18.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
三、解答题(本大题共6小题,共58分)
19.(8分)观察下列等式:,,,……
(1)探索这些等式中的规律,直接写出第n个等式(用含n的等式表示).
(2)试说明你的结论的正确性.
20.(8分)如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作△BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).
21.(10分)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.
22.(10分)如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
23.(10分)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示).
(2)用等式表示线段MB与 PQ之间的数量关系,并证明.
24.(12分)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在中,,,边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图1):
(1)延长到Q使得;(2)再连接,把集中在中;(3)利用三角形的三边关系可得的取值范围,进而求出的取值范围.
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
求出的取值范围.
求如图中与的位置关系并证明;
思考:已知,如图,是的中线,,,,试探究线段与的关系,并证明.
参考答案
一、单选题
1.D
解:四个人共有6场比赛,由于甲、乙、丙三人胜的场数相同,所以只有两种可能性:甲胜1场或甲胜2场;由此进行分析即可.
详解:四个人共有6场比赛,由于甲、乙、丙三人胜的场数相同,
所以只有两种可能性:甲胜1场或甲胜2场;
若甲只胜一场,这时乙、丙各胜一场,说明丁胜三场,这与甲胜丁矛盾,
所以甲只能是胜两场,
即:甲、乙、丙各胜2场,此时丁三场全败,也就是胜0场.
答:甲、乙、丙各胜2场,此时丁三场全败,丁胜0场.
故选D.
2.D
【分析】根据平行线的判定方法一一判断即可.
解:A、由作图可知,内错角相等两直线平行,本选项不符合题意.
B、由作图可知,同位角相等两直线平行,本选项不符合题意.
C、与作图可知,垂直于同一条直线的两条直线平行,本选项不符合题意,
D、无法判断两直线平行,
故选:D.
3.B
解:根据同位角相等,两直线平行,可得B.
4.C
解:设三角形的三个内角分别为:2x,7x,4x.
∵三角形三个内角度数的比为2:7:4,
∴2x+7x+4x=180°,
∴7x≈97°,
∴这个三角形是钝角三角形.故选C
5.C
【分析】根据垂直的定义和余角的定义列式计算得到,根据两直线平行,同位角相等可得.
解:如图,
直线,
.
,
,
直线,
,
故选C.
6.B
【分析】根据平行线的性质,得出,,根据全等三角形的判定,得出,根据全等三角形的性质,得出,根据,,即可求线段的长.
解:∵,
∴,,
在和中,
∴,
∴,
∵,
∴.
故选B.
7.A
【分析】根据相反数是它本身的数为0;倒数等于这个数本身是±1;平方等于它本身的数为1和0;算术平方根等于本身的数为1和0进行分析即可.
解:A、如果一个数的相反数等于这个数本身,那么这个数一定是0,是真命题;
B、如果一个数的倒数等于这个数本身,那么这个数一定是1,是假命题;
C、如果一个数的平方等于这个数本身,那么这个数一定是0,是假命题;
D、如果一个数的算术平方根等于这个数本身,那么这个数一定是0,是假命题;
故选A.
8.C
【分析】根据,可得再根据三角形内角和即可得出答案.
解:由图可得
∵,
∴
∴
故选:C.
9.C
【分析】根据三角形的内角和定理和三角形外角性质进行解答即可.
解:如图:
,,
,,
∴
=
=,
故选C.
10.A
【分析】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°,依据∠BAC=50°,AE平分∠BAC,即可得到∠DAE=5°,再根据△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,可得∠EAD+∠ACD=75°.
解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°,
故选:A.
二、填空题
11.如果两个角是同一个角的补角,那么这两个角相等.
【分析】每一个命题都是基于条件的一个判断,只要把条件部分和判断部分分开即可.
解:如果两个角是同一个角的补角,那么这两个角相等,
故答案为:如果两个角是同一个角的补角,那么这两个角相等.
12.1024
解:分析:根据题意可得每次挑选都是去掉偶数,进而得出需要挑选的总次数进而得出答案.
详解:∵将这些金蛋按1﹣2018的顺序进行标号,第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,
∴剩余的数字都是偶数,是2的倍数,;
∵他将剩下的金蛋在原来的位置上又按1﹣1009编了号,
又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋,
∴剩余的数字为4的倍数,
以此类推:2018→1009→504→252→126→63→31→15→7→3→1
共经历10次重新编号,故最后剩余的数字为:210=1024.
故答案为1024.
13.∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE
【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此进行判断(答案不唯一).
解:若,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD;
故答案为∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)
14. 50° 40°
解:∵DE∥AB,∠ACD=50°,
∴∠A=∠ACD=50°,
∵∠ACB=90°,
∴∠B=90°-∠A=90°-50°=40°.
15.71°
解:∵在Rt△ABC中,∠ACB=90°,∠A=26°,
∴∠B=64°,
∵将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,∠ACB=90°,
∴∠BCD=∠ECD=45°,∠CED=∠B=64°,
∴∠CDE=180°﹣∠ECD﹣∠CED=71°,
故答案为71°.
16.117°
【分析】根据三角形的三个内角和为180°,以及α=2γ,可得出β与γ的关系式,再根据α≥β≥γ,得出α≥180°-3γ≥γ,从而求出γ的取值范围.
解:∵α+β+γ=180°,
∴β=180°-α-γ=180°-3γ,
所以α≥180°-3γ≥γ,
∴5γ≥180°≥4γ,
45°≥γ≥36°,
所以72°≥β≥45°,
∴β的最大值与最小值的和=72°+45°=117°,
故答案为117°.
17. ①②③ ④
解:解题设:①②③;结论:④.
证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF.
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),∴∠1=∠2.
此题可以分成三种情况:
情况一:题设:①②③;结论:④,可以利用SAS定理证明△ABC≌△DEF.
情况二:题设:①③④;结论:②,可以利用AAS证明△ABC≌△DEF:
在△ABC和△DEF中,∵ AB=DE,∠B=∠E,∠1=∠2,∴△ABC≌△DEF(AAS).
∴BC=EF,∴BC-FC=EF-FC,即BF=EC.
情况三:题设:②③④;结论:①,可以利用ASA证明△ABC≌△DEF,再根据全等三角形的
性质可推出结论:
∵BF=EC,∴BF+CF=EC+CF,即BC=EF.
在△ABC和△DEF中,∵∠B=∠E ,BC=EF,∠1=∠2,∴△ABC≌△DEF(ASA).∴AB=DE.
18.40°
【分析】先根据角平分线的定义得到∠OBC=∠ABC,∠OCB=∠ACB,再根据三角形内角和定理得∠BOC+∠OBC+∠OCB=180°,则∠BOC=180°﹣(∠ABC+∠ACB),由于∠ABC+∠ACB=180°﹣∠A,所以∠BOC=90°+∠A,然后把∠BOC=110°代入计算可得到∠A的度数.
解:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣(180°﹣∠A)=90°+∠A,
而∠BOC=110°,
∴90°+∠A=110°
∴∠A=40°.
故答案为40°.
三、解答题
19.
解:(1)猜想:;
(2)证:右边===左边,即
20.
解:(1)如图所示:
(2)DE∥AC
∵DE平分∠BDC,
∴∠BDE=∠BDC,
∵∠ACD=∠A,∠ACD+∠A=∠BDC,
∴∠A=∠BDC,
∴∠A=∠BDE,
∴DE∥AC.
21.
解:证明:∵AF=DC,
∴AC+FC=FC+DF,
∴AC=DF,
又∵AB=DE,∠A=∠D,
∴△ACB≌△DEF(SAS),
∴∠ACB=∠DFE,
∴BC∥EF.
22.
解:(1)证明:∵BF=EC,
∴BF+CF=CF+CE,
∴BC=EF
∵AB=DE,AC=DF
∴△ABC≌△DEF(SSS)
(2)AB∥DE,AC∥DF,理由如下,
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.
23.
解:(1) ∠AMQ=45°+α.理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠PAB=45°-α,∠AHM=90°,
∴∠AMQ=180°-∠AHM-∠PAM=45°+α;
(2)线段MB与PQ之间的数量关系:PQ=MB.
理由如下:
连接AQ,过点M作ME⊥QB,
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=α+45°=∠AMQ,
∴AP=AQ=QM,
在Rt△APC和Rt△QME中,
∴Rt△APC≌Rt△QME,
∴PC=ME,
∴△MEB是等腰直角三角形,
∴,
∴PQ=MB.
24.
(1)解:∵是的中线,
∴,
在和中,
,
∴,
∴,
在中,,
∴,
∴,
故答案为;
(2)解:,理由:由(1)知,,
∴,
∴;
(3)解:,,
理由:如图2,延长到Q使得,连接,
由(1)知,,
∴,
∵,
∴,
在中,,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
延长交于P,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
即:.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
