人教版六年级下册数学总复习图形的认识课件(共16张PPT)
文档属性
| 名称 | 人教版六年级下册数学总复习图形的认识课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 863.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 06:39:54 | ||
图片预览




文档简介
(共16张PPT)
第六单元 整理和复习
图形的认识与测量
第一课时
复习导入
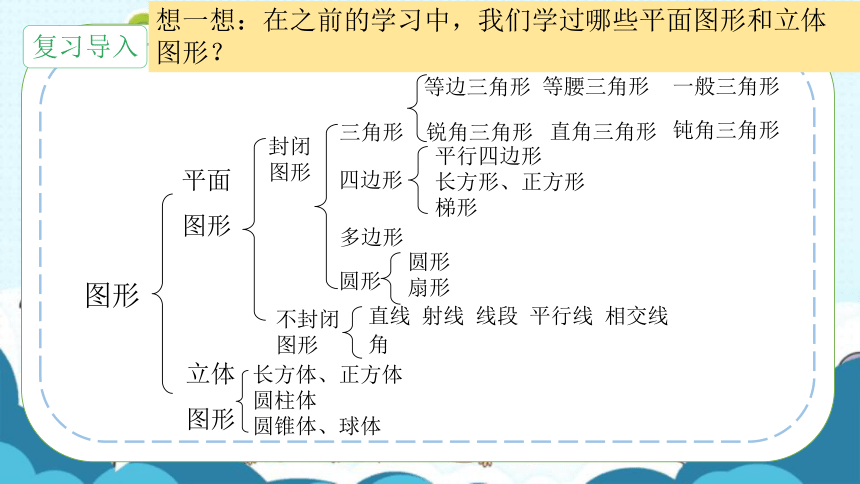
图形
平面
图形
长方体、正方体
圆柱体
圆锥体、球体
封闭图形
不封闭
图形
立体
图形
三角形
平行四边形
长方形、正方形
梯形
锐角三角形
钝角三角形
直角三角形
四边形
多边形
圆形
圆形
扇形
直线 射线 线段 平行线 相交线
角
等边三角形
等腰三角形
一般三角形
想一想:在之前的学习中,我们学过哪些平面图形和立体图形?
独立思考,小组讨论
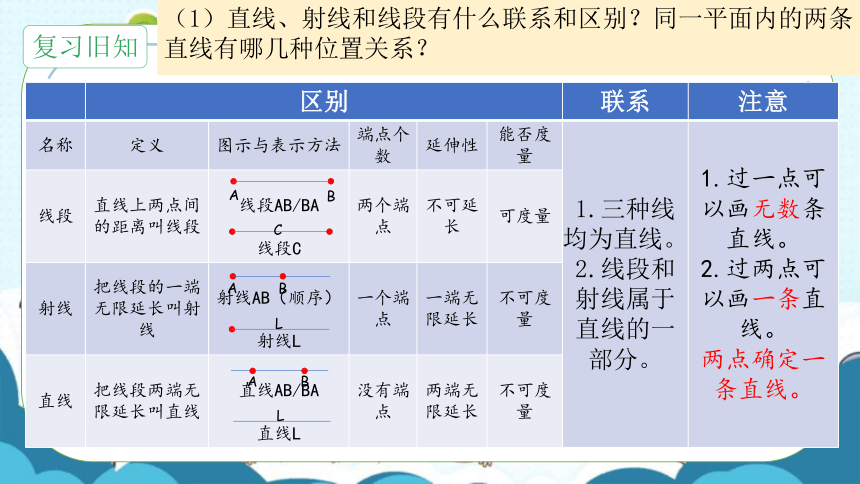
(1)直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
(2)我们学过哪些角?在放大镜下看角,它的大小会变化吗?
(3)关于三角形,你知道些什么?
(4)关于平行四边形,你知道些什么?
(5)圆与上面的平面图形有什么不同?圆有哪些特点?
复习旧知
(1)直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
区别 联系 注意
名称 定义 图示与表示方法 端点个数 延伸性 能否度量 1.三种线均为直线。 2.线段和射线属于直线的一部分。 1.过一点可以画无数条直线。
2.过两点可以画一条直线。
两点确定一条直线。
线段 直线上两点间的距离叫线段 线段AB/BA 线段C 两个端点 不可延长 可度量 射线 把线段的一端无限延长叫射线 射线AB(顺序) 射线L 一个端点 一端无限延长 不可度量 直线 把线段两端无限延长叫直线 直线AB/BA 直线L 没有端点 两端无限延长 不可度量
A
B
C
A
B
L
L
A
B
复习旧知
(1)直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
区别 联系 注意
名称 定义 图示与表示方法 端点个数 延伸性 能否度量 1.三种线均为直线。 2.线段和射线属于直线的一部分。 1.过一点可以画无数条直线。
2.过两点可以画一条直线。
两点确定一条直线。
线段 直线上两点间的距离叫线段 线段AB/BA 线段C 两个端点 不可延长 可度量 射线 把线段的一端无限延长叫射线 射线AB(顺序) 射线L 一个端点 一端无限延长 不可度量 直线 把线段两端无限延长叫直线 直线AB/BA 直线L 没有端点 两端无限延长 不可度量
A
B
C
A
B
L
L
A
B
同一平面内两条直线的位置关系
两条直线
平行
平行线:同一平面内不相交的两条直线。
相交
垂直:
不垂直
两条直线相交,如果有一个角是直角,那么这两条直线互相垂直。
点到直线间的距离
1.从直线外的一点P,到这条直线可以画无数条线段。其中,垂直线段最短。
2.从直线外一点到这条直线作一条垂线,这点和垂足间的长度,叫做点到直线的距离。
3.过直线外或直线上一点,有且只有1条直线和已知直线垂直。
P
巩固练习
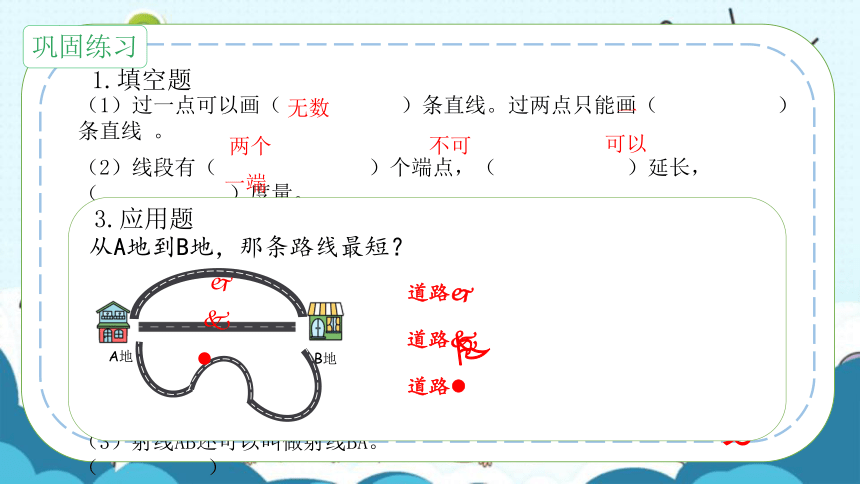
(1)过一点可以画( )条直线。过两点只能画( )条直线 。
(2)线段有( )个端点,( )延长,( )度量。
(3)把线段( )无限延长叫射线。
(4)( )确定一条直线。
(5)平行线是同一平面内( )的两条直线。
无数
一
1.填空题
2.判断题
不可
两个
可以
一端
两点
(1)线段和直线都属于射线的一部分。 ( )
(2)把线段两端无限延长叫直线。 ( )
(3)射线AB还可以叫做射线BA。 ( )
(4)相交的两条线是垂直的两条线。 ( )
A
B
不相交
从A地到B地,那条路线最短?
3.应用题
A地
B地
道路
道路
道路
复习旧知
(2)我们学过哪些角?在放大镜下看角,它的大小会变化吗?
1.角的定义:
从一点引出两条射线所组成的图形叫做角。
2.角的特点:
有一个顶点,两条边。
顶点
边
3.角的分类:
类型 锐角 直角 钝角 平角 周角
图形
大小 小于90° 等于90° 大于90°小于180° 等于180° 等于360°
4.角的度量:
5.角的画法:
(1)角的大小与两条边张开的大小有关,与边的长短无关。
(2)角的大小可以用量角器进行测量。
(3)把量角器的中心和角的顶点重合,把量角器的0°刻度线与角的另一边重合,角的另一边所对的量角器的刻度,就是这个角的度数。
(1)画一条射线。
(2)把量角器的中心和射线的端点重合。0°刻度线与射线重合。
(3)在量角器所画角的刻度线出点一个点。
(4)以原射线的端点为端点,经过刚才的点画射线。
60°
不会,放大镜只会放大边长,不会放大两条边张开的大小。
巩固练习
(1)角有( )个顶点,( )条边。
(2)角有五种,分别是( )、( )、( )、( )、( )。
(3)4:00时,时针和分针的夹角是( )角;9:00时,时针和分针的夹角是( )°;时针从1走到2,分针走了( )°;6:00时,时针和分针的夹角是( )°。
1.填空题
2.判断题
一
锐角
直角
(1)从一个点引出两条直线做组成的图形叫角。 ( )
(2)两条边越长,角的度数越大。 ( )
(3)2:00时,时针和分针的夹角是60°。 ( )
(4)度量锐角时,0°刻度线要与底边的射线对齐。 ( )
钝
90
30
180
钝角
右图中有( )个直角,( )个锐角,
( )个钝角,( )个平角 。
3.提升题
3
4
2
2
两
平角
周角
复习旧知
(3)关于三角形,你知道些什么?
1.三角形的定义:
由三条线段首尾顺次相连围场的封闭图形叫三角形。
边
边
边
三角形
内角和180°
2.三角形的特点:
(1)三角形有三个顶点、三条边、三个内角。三个内角的和为180°。
(3)三角形三条边的关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
(4)从顶点向对边的垂线段是三角形的高,三角形有三条高。
(2)三角形具有稳定性,不易变形。
3.三角形的分类:
(1)按角分。
(2)按边分。
锐角三角形
直角
三角形
钝角
三角形
一般三角形
等腰三角形
等边三角形
直角三角形的两个锐角的和是90°
等边三角形的每个锐角都是60°,有3条对称轴;等腰三角形有1条对称轴。
巩固练习
在第一个三角形上,标上三角形各部分的名称,并把作出下面所有三角形底边对应的高。
1.画图题
2.判断题
下面哪组小棒可以拼成三角形?在能拼成三角形的括号里话“ ”。
1㎝
7㎝
9㎝
( )
5㎝
10㎝
13㎝
( )
复习旧知
(4)关于平行四边形,你知道些什么?
四边形
平行四边形
梯形
定义:在同一平面内,两组对边分别平行的四边形叫做平行四边形。
特点:1.具有不稳定性
2.长方形、正方形是特殊的平行四边形。
长方形
正方形
定义:由四条线段围成的,且四个角都是直角的平行四边形叫长方形。
定义:由四条线段围成的,四个角都是直角,四条边相等的平行四边形叫正方形。
特点:长方形有两条对称轴。
特点:正方形有4条对称轴,且对边相等。
定义:只有一组对边平行的四边形叫梯形。
分类:等腰梯形、直角梯形。
特点:等腰梯形有一条对称轴。
四条线段围成的图形
巩固练习
(1)长方形有( )条对称轴,正方形有( )条对称轴。
(2)学校的伸缩门用到了平行四边形的( )性,起重机吊臂上的三角形结构用到了三角形的( )性。
(3)把一个长方形按照一定的比例放大或缩小后,( )发生了变化,( )没有变化。
1.填空题
两
(1)两个梯形一定能拼成一个平行四边形。 ( )
(2)有一组对边平行的四边形是梯形。 ( )
(3)四条边相等的四边形一定是正方形。 ( )
(4)梯形有一条对称轴。 ( )
四
不稳定
稳定
大小
形状
2.判断题
复习旧知
(5)圆与上面的平面图形有什么不同?圆有哪些特点?
1.圆形的定义:
圆是平面上的封闭曲线图形。
半径r
圆心O
直径d
2.圆形的各部分名称:
(1)圆心:圆中心的一点叫做圆心,点O是圆心。
(2)半径:连接圆心和圆上任意一点的线段叫做半径,用字母r表示半径。
(3)直径:通过圆心且两端都在圆上的线段叫做直径,用字母d表示直径。
3.圆的特点:
(1)圆心确定圆的位置,半径决定圆的大小。
(2)同圆或等圆中,半径是直径的一半,直径是半径的两倍。
(3)圆是轴对称图形,圆的直径所在的直线是它的对称轴,它有无数条对称轴。
扇形的定义
由圆心角的两条半径和圆心角所对的弧围成的图形叫扇形。
半径r
A
弧
B
巩固练习
(1)用圆规画出半径为5厘米的圆,并标上各部分的名称。
1.画图题
(1)画一个半径是4cm的圆时,圆规两脚间的距离是2厘米。 ( )
(2)一个圆至少对折2次才能找到圆心。 ( )
(3)圆的半径是直径的两倍,圆的直径是半径的一半。 ( )
(4)扇形有一条弧,两条边。 ( )
2.判断题
做一做
做两个同样的平行四边形纸片。把它们上下重合放置,将上方的平行四边形绕它的一个顶点旋转180°,再通过平移使它与另一个平行四边形上下重合。观察两个平行四边形的各条边与各个角,你有什么发现?
A
B
A
B
A
B
B
B
A
答:1.平行四边形的对边相等,对角也相等。
2.旋转、平移前后的图形形状和大小不变。
课后作业
必做题
1.完成图形的认识的试卷。
2.整理思维导图。
选做题
制作手抄报。
第六单元 整理和复习
图形的认识与测量
第一课时
复习导入
图形
平面
图形
长方体、正方体
圆柱体
圆锥体、球体
封闭图形
不封闭
图形
立体
图形
三角形
平行四边形
长方形、正方形
梯形
锐角三角形
钝角三角形
直角三角形
四边形
多边形
圆形
圆形
扇形
直线 射线 线段 平行线 相交线
角
等边三角形
等腰三角形
一般三角形
想一想:在之前的学习中,我们学过哪些平面图形和立体图形?
独立思考,小组讨论
(1)直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
(2)我们学过哪些角?在放大镜下看角,它的大小会变化吗?
(3)关于三角形,你知道些什么?
(4)关于平行四边形,你知道些什么?
(5)圆与上面的平面图形有什么不同?圆有哪些特点?
复习旧知
(1)直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
区别 联系 注意
名称 定义 图示与表示方法 端点个数 延伸性 能否度量 1.三种线均为直线。 2.线段和射线属于直线的一部分。 1.过一点可以画无数条直线。
2.过两点可以画一条直线。
两点确定一条直线。
线段 直线上两点间的距离叫线段 线段AB/BA 线段C 两个端点 不可延长 可度量 射线 把线段的一端无限延长叫射线 射线AB(顺序) 射线L 一个端点 一端无限延长 不可度量 直线 把线段两端无限延长叫直线 直线AB/BA 直线L 没有端点 两端无限延长 不可度量
A
B
C
A
B
L
L
A
B
复习旧知
(1)直线、射线和线段有什么联系和区别?同一平面内的两条直线有哪几种位置关系?
区别 联系 注意
名称 定义 图示与表示方法 端点个数 延伸性 能否度量 1.三种线均为直线。 2.线段和射线属于直线的一部分。 1.过一点可以画无数条直线。
2.过两点可以画一条直线。
两点确定一条直线。
线段 直线上两点间的距离叫线段 线段AB/BA 线段C 两个端点 不可延长 可度量 射线 把线段的一端无限延长叫射线 射线AB(顺序) 射线L 一个端点 一端无限延长 不可度量 直线 把线段两端无限延长叫直线 直线AB/BA 直线L 没有端点 两端无限延长 不可度量
A
B
C
A
B
L
L
A
B
同一平面内两条直线的位置关系
两条直线
平行
平行线:同一平面内不相交的两条直线。
相交
垂直:
不垂直
两条直线相交,如果有一个角是直角,那么这两条直线互相垂直。
点到直线间的距离
1.从直线外的一点P,到这条直线可以画无数条线段。其中,垂直线段最短。
2.从直线外一点到这条直线作一条垂线,这点和垂足间的长度,叫做点到直线的距离。
3.过直线外或直线上一点,有且只有1条直线和已知直线垂直。
P
巩固练习
(1)过一点可以画( )条直线。过两点只能画( )条直线 。
(2)线段有( )个端点,( )延长,( )度量。
(3)把线段( )无限延长叫射线。
(4)( )确定一条直线。
(5)平行线是同一平面内( )的两条直线。
无数
一
1.填空题
2.判断题
不可
两个
可以
一端
两点
(1)线段和直线都属于射线的一部分。 ( )
(2)把线段两端无限延长叫直线。 ( )
(3)射线AB还可以叫做射线BA。 ( )
(4)相交的两条线是垂直的两条线。 ( )
A
B
不相交
从A地到B地,那条路线最短?
3.应用题
A地
B地
道路
道路
道路
复习旧知
(2)我们学过哪些角?在放大镜下看角,它的大小会变化吗?
1.角的定义:
从一点引出两条射线所组成的图形叫做角。
2.角的特点:
有一个顶点,两条边。
顶点
边
3.角的分类:
类型 锐角 直角 钝角 平角 周角
图形
大小 小于90° 等于90° 大于90°小于180° 等于180° 等于360°
4.角的度量:
5.角的画法:
(1)角的大小与两条边张开的大小有关,与边的长短无关。
(2)角的大小可以用量角器进行测量。
(3)把量角器的中心和角的顶点重合,把量角器的0°刻度线与角的另一边重合,角的另一边所对的量角器的刻度,就是这个角的度数。
(1)画一条射线。
(2)把量角器的中心和射线的端点重合。0°刻度线与射线重合。
(3)在量角器所画角的刻度线出点一个点。
(4)以原射线的端点为端点,经过刚才的点画射线。
60°
不会,放大镜只会放大边长,不会放大两条边张开的大小。
巩固练习
(1)角有( )个顶点,( )条边。
(2)角有五种,分别是( )、( )、( )、( )、( )。
(3)4:00时,时针和分针的夹角是( )角;9:00时,时针和分针的夹角是( )°;时针从1走到2,分针走了( )°;6:00时,时针和分针的夹角是( )°。
1.填空题
2.判断题
一
锐角
直角
(1)从一个点引出两条直线做组成的图形叫角。 ( )
(2)两条边越长,角的度数越大。 ( )
(3)2:00时,时针和分针的夹角是60°。 ( )
(4)度量锐角时,0°刻度线要与底边的射线对齐。 ( )
钝
90
30
180
钝角
右图中有( )个直角,( )个锐角,
( )个钝角,( )个平角 。
3.提升题
3
4
2
2
两
平角
周角
复习旧知
(3)关于三角形,你知道些什么?
1.三角形的定义:
由三条线段首尾顺次相连围场的封闭图形叫三角形。
边
边
边
三角形
内角和180°
2.三角形的特点:
(1)三角形有三个顶点、三条边、三个内角。三个内角的和为180°。
(3)三角形三条边的关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
(4)从顶点向对边的垂线段是三角形的高,三角形有三条高。
(2)三角形具有稳定性,不易变形。
3.三角形的分类:
(1)按角分。
(2)按边分。
锐角三角形
直角
三角形
钝角
三角形
一般三角形
等腰三角形
等边三角形
直角三角形的两个锐角的和是90°
等边三角形的每个锐角都是60°,有3条对称轴;等腰三角形有1条对称轴。
巩固练习
在第一个三角形上,标上三角形各部分的名称,并把作出下面所有三角形底边对应的高。
1.画图题
2.判断题
下面哪组小棒可以拼成三角形?在能拼成三角形的括号里话“ ”。
1㎝
7㎝
9㎝
( )
5㎝
10㎝
13㎝
( )
复习旧知
(4)关于平行四边形,你知道些什么?
四边形
平行四边形
梯形
定义:在同一平面内,两组对边分别平行的四边形叫做平行四边形。
特点:1.具有不稳定性
2.长方形、正方形是特殊的平行四边形。
长方形
正方形
定义:由四条线段围成的,且四个角都是直角的平行四边形叫长方形。
定义:由四条线段围成的,四个角都是直角,四条边相等的平行四边形叫正方形。
特点:长方形有两条对称轴。
特点:正方形有4条对称轴,且对边相等。
定义:只有一组对边平行的四边形叫梯形。
分类:等腰梯形、直角梯形。
特点:等腰梯形有一条对称轴。
四条线段围成的图形
巩固练习
(1)长方形有( )条对称轴,正方形有( )条对称轴。
(2)学校的伸缩门用到了平行四边形的( )性,起重机吊臂上的三角形结构用到了三角形的( )性。
(3)把一个长方形按照一定的比例放大或缩小后,( )发生了变化,( )没有变化。
1.填空题
两
(1)两个梯形一定能拼成一个平行四边形。 ( )
(2)有一组对边平行的四边形是梯形。 ( )
(3)四条边相等的四边形一定是正方形。 ( )
(4)梯形有一条对称轴。 ( )
四
不稳定
稳定
大小
形状
2.判断题
复习旧知
(5)圆与上面的平面图形有什么不同?圆有哪些特点?
1.圆形的定义:
圆是平面上的封闭曲线图形。
半径r
圆心O
直径d
2.圆形的各部分名称:
(1)圆心:圆中心的一点叫做圆心,点O是圆心。
(2)半径:连接圆心和圆上任意一点的线段叫做半径,用字母r表示半径。
(3)直径:通过圆心且两端都在圆上的线段叫做直径,用字母d表示直径。
3.圆的特点:
(1)圆心确定圆的位置,半径决定圆的大小。
(2)同圆或等圆中,半径是直径的一半,直径是半径的两倍。
(3)圆是轴对称图形,圆的直径所在的直线是它的对称轴,它有无数条对称轴。
扇形的定义
由圆心角的两条半径和圆心角所对的弧围成的图形叫扇形。
半径r
A
弧
B
巩固练习
(1)用圆规画出半径为5厘米的圆,并标上各部分的名称。
1.画图题
(1)画一个半径是4cm的圆时,圆规两脚间的距离是2厘米。 ( )
(2)一个圆至少对折2次才能找到圆心。 ( )
(3)圆的半径是直径的两倍,圆的直径是半径的一半。 ( )
(4)扇形有一条弧,两条边。 ( )
2.判断题
做一做
做两个同样的平行四边形纸片。把它们上下重合放置,将上方的平行四边形绕它的一个顶点旋转180°,再通过平移使它与另一个平行四边形上下重合。观察两个平行四边形的各条边与各个角,你有什么发现?
A
B
A
B
A
B
B
B
A
答:1.平行四边形的对边相等,对角也相等。
2.旋转、平移前后的图形形状和大小不变。
课后作业
必做题
1.完成图形的认识的试卷。
2.整理思维导图。
选做题
制作手抄报。
