北京市朝阳区2015-2016学年高一上学期期末考试数学试卷
文档属性
| 名称 | 北京市朝阳区2015-2016学年高一上学期期末考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 386.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-02 18:40:10 | ||
图片预览



文档简介
北京市朝阳区2015-2016学年度第一学期期末高一年级统一考试
数学试卷 2016.1
(考试时间100分钟 满分120分)
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)下列各组中的两个集合和,表示同一集合的是
(A),
(B),
(C),
(D),
(2)若,,则下列不等式中成立的是
(A) (B) (C) (D)
(3)函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确度)为
(A) (B) (C) (D)
(4)某程序框图如图所示,若输出的,则判断框内为
(A)? (B)?
(C) (D)
(5)给定函数①,②,③,④,其中在区间上单调递减的函数序号是
(A)①④ (B)②④ (C)②③ (D)①③
(6)已知,,,则,,三者的大小关系是
(A) (B)
(C) (D)
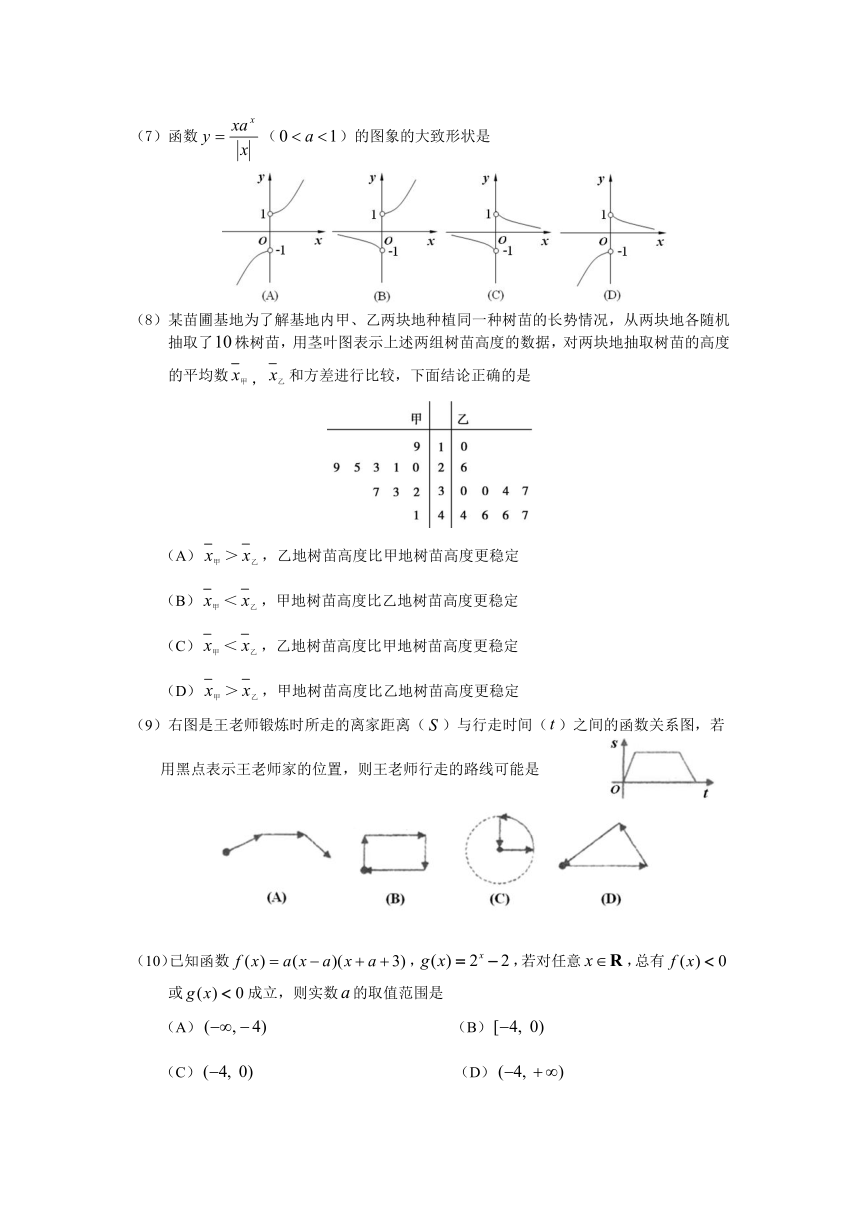
(7)函数()的图象的大致形状是
( http: / / www.21cnjy.com )
(8)某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数,和方差进行比较,下面结论正确的是
( http: / / www.21cnjy.com )
(A)>,乙地树苗高度比甲地树苗高度更稳定
(B)<,甲地树苗高度比乙地树苗高度更稳定
(C)<,乙地树苗高度比甲地树苗高度更稳定
(D)>,甲地树苗高度比乙地树苗高度更稳定
(9)右图是王老师锻炼时所走的离家距离()与行走时间()之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是
( http: / / www.21cnjy.com )
(10)已知函数,,若对任意,总有 或成立,则实数的取值范围是
(A) (B)
(C) (D)
第二部分(非选择题 共70分)
二、填空题:本大题共6小题,每小题5分,共30分.
(11)已知函数 则的值是________.
(12)从某小学随机抽取100名同学,将他们的身高(单
位:厘米)数据绘制成频率分布直方图(如图).
由图中数据可知 .若要从身高在
,,三组内的学
生中,用分层抽样的方法选取人参加一项活动,
则从身高在内的学生中选取的人数应为 .
(13)设,则函数的最大值为 .
(14)如图,一不规则区域内,有一边长为米的正方形,向区域内随机地撒颗黄豆,数得落在正方形区域内(含边界)的黄豆数为颗,以此实验数据为依据可以估计出该不规则图形的面积为 平方米.(用分数作答)
(15)若函数的图象关于轴对称,则 .
(16)关于函数 有以下四个命题:
①对于任意的,都有;
②函数是偶函数;
③若为一个非零有理数,则对任意恒成立;
④在图象上存在三个点,,,使得为等边三角形.
其中正确命题的序号是 .
三、解答题:本大题共4小题,共40分.
(17)(本题满分9分)
已知函数的定义域为集合,函数的定义域为集合.
(Ⅰ)当时,求;
(Ⅱ)若,求实数的值.
(18)(本题满分9分)
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,表示空气污染越严重:
PM2.5日均浓度 0~35 35~75 75~115 115~150 150~250 >250
空气质量级别 一级 二级 三级 四级 五级 六级
空气质量类别 优 良 轻度污染 中度污染 重度污染 严重污染
某市2013年3月8日—4月7日(30天)对空气质量
指数PM2.5进行检测,获得数据后整理得到如下条形图:
(Ⅰ)估计该城市一个月内空气质量类别为良的概率;
(Ⅱ)从空气质量级别为三级和四级的数据中任取2个,求
至少有一天空气质量类别为中度污染的概率.
(19)(本题满分10分)
已知定义域为的单调减函数是奇函数,当时,.
(Ⅰ)求的值;
(Ⅱ)求的解析式;
(Ⅲ)若对任意的,不等式恒成立,求实数的取值范围.
(20)(本题满分12分)
定义在上的函数,如果对任意,都有()成立,则称为阶伸缩函数.
(Ⅰ)若函数为二阶伸缩函数,且当时,,求 的值;
(Ⅱ)若函数为三阶伸缩函数,且当时,,求证:函数在上无零点;
(Ⅲ)若函数为阶伸缩函数,且当时,的取值范围是,求在()上的取值范围.
北京市朝阳区2015-2016学年度第一学期期末高一年级统一考试
数学试题答案及评分标准 2016.1
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C A B A D B C C
二、填空题:本大题共6小题,每小题5分,共30分.
题号 11 12 13 14 15 16
答案 ①②③④
注:(12)题第一空3分,第二空2分.
三、解答题:本大题共4小题,共40分.
(17)解:(Ⅰ)由的定义域得.
当时,,
则.
所以. ……………………………… 6分
(Ⅱ)因为,,
所以有.
解得.
此时,符合题意.
所以. ……………………………… 9分
(18)解:(Ⅰ)由条形监测图可知,空气质量级别为良的天数为16天,
所以此次监测结果中空气质量为良的概率为; ………3分
(Ⅱ)样本中空气质量级别为三级的有4天,设其编号为,,,;
样本中空气质量级别为四级的有2天,设其编号为,,
则基本事件有:
,,,,,,,,,,,,,,共15个.
其中至少有一天空气质量类别为中度污染的情况有:
,,,,,,,,
共9个.
所以至少有一天空气质量类别为中度污染的概率为. ……………9分
(19)解:(Ⅰ)因为定义域为的函数是奇函数,
所以. ……………………………………2分
(Ⅱ)因为当时,,
所以.
又因为函数是奇函数,所以.
所以.
综上, ……………………………………6分
(Ⅲ)由得.
因为是奇函数, 所以.又在上是减函数,所以.
即对任意恒成立.
【方法一】令,则.由,解得.
【方法二】即对任意恒成立. 令,
则
故实数的取值范围为. ……………………………………10分
(20)解:(Ⅰ)由题设,当时,,
所以.
因为函数为二阶伸缩函数,
所以对任意,都有.
所以. ……………………………4分
(Ⅱ)当()时,.
由为三阶伸缩函数,有.
注意到时,.
所以.
令,解得或,它们均不在内. ……7分
所以函数在上无零点. ……………………………8分
(Ⅲ) 由题设,若函数为阶伸缩函数,有,
且当时, 的取值范围是.
所以当时,.
因为, 所以.
所以当时,.
当时,即,
则使,
,即,
.
又,
,即.
因为,
所以在()上的取值范围是.……………12分
数学试卷 2016.1
(考试时间100分钟 满分120分)
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)下列各组中的两个集合和,表示同一集合的是
(A),
(B),
(C),
(D),
(2)若,,则下列不等式中成立的是
(A) (B) (C) (D)
(3)函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确度)为
(A) (B) (C) (D)
(4)某程序框图如图所示,若输出的,则判断框内为
(A)? (B)?
(C) (D)
(5)给定函数①,②,③,④,其中在区间上单调递减的函数序号是
(A)①④ (B)②④ (C)②③ (D)①③
(6)已知,,,则,,三者的大小关系是
(A) (B)
(C) (D)
(7)函数()的图象的大致形状是
( http: / / www.21cnjy.com )
(8)某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数,和方差进行比较,下面结论正确的是
( http: / / www.21cnjy.com )
(A)>,乙地树苗高度比甲地树苗高度更稳定
(B)<,甲地树苗高度比乙地树苗高度更稳定
(C)<,乙地树苗高度比甲地树苗高度更稳定
(D)>,甲地树苗高度比乙地树苗高度更稳定
(9)右图是王老师锻炼时所走的离家距离()与行走时间()之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是
( http: / / www.21cnjy.com )
(10)已知函数,,若对任意,总有 或成立,则实数的取值范围是
(A) (B)
(C) (D)
第二部分(非选择题 共70分)
二、填空题:本大题共6小题,每小题5分,共30分.
(11)已知函数 则的值是________.
(12)从某小学随机抽取100名同学,将他们的身高(单
位:厘米)数据绘制成频率分布直方图(如图).
由图中数据可知 .若要从身高在
,,三组内的学
生中,用分层抽样的方法选取人参加一项活动,
则从身高在内的学生中选取的人数应为 .
(13)设,则函数的最大值为 .
(14)如图,一不规则区域内,有一边长为米的正方形,向区域内随机地撒颗黄豆,数得落在正方形区域内(含边界)的黄豆数为颗,以此实验数据为依据可以估计出该不规则图形的面积为 平方米.(用分数作答)
(15)若函数的图象关于轴对称,则 .
(16)关于函数 有以下四个命题:
①对于任意的,都有;
②函数是偶函数;
③若为一个非零有理数,则对任意恒成立;
④在图象上存在三个点,,,使得为等边三角形.
其中正确命题的序号是 .
三、解答题:本大题共4小题,共40分.
(17)(本题满分9分)
已知函数的定义域为集合,函数的定义域为集合.
(Ⅰ)当时,求;
(Ⅱ)若,求实数的值.
(18)(本题满分9分)
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,表示空气污染越严重:
PM2.5日均浓度 0~35 35~75 75~115 115~150 150~250 >250
空气质量级别 一级 二级 三级 四级 五级 六级
空气质量类别 优 良 轻度污染 中度污染 重度污染 严重污染
某市2013年3月8日—4月7日(30天)对空气质量
指数PM2.5进行检测,获得数据后整理得到如下条形图:
(Ⅰ)估计该城市一个月内空气质量类别为良的概率;
(Ⅱ)从空气质量级别为三级和四级的数据中任取2个,求
至少有一天空气质量类别为中度污染的概率.
(19)(本题满分10分)
已知定义域为的单调减函数是奇函数,当时,.
(Ⅰ)求的值;
(Ⅱ)求的解析式;
(Ⅲ)若对任意的,不等式恒成立,求实数的取值范围.
(20)(本题满分12分)
定义在上的函数,如果对任意,都有()成立,则称为阶伸缩函数.
(Ⅰ)若函数为二阶伸缩函数,且当时,,求 的值;
(Ⅱ)若函数为三阶伸缩函数,且当时,,求证:函数在上无零点;
(Ⅲ)若函数为阶伸缩函数,且当时,的取值范围是,求在()上的取值范围.
北京市朝阳区2015-2016学年度第一学期期末高一年级统一考试
数学试题答案及评分标准 2016.1
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C A B A D B C C
二、填空题:本大题共6小题,每小题5分,共30分.
题号 11 12 13 14 15 16
答案 ①②③④
注:(12)题第一空3分,第二空2分.
三、解答题:本大题共4小题,共40分.
(17)解:(Ⅰ)由的定义域得.
当时,,
则.
所以. ……………………………… 6分
(Ⅱ)因为,,
所以有.
解得.
此时,符合题意.
所以. ……………………………… 9分
(18)解:(Ⅰ)由条形监测图可知,空气质量级别为良的天数为16天,
所以此次监测结果中空气质量为良的概率为; ………3分
(Ⅱ)样本中空气质量级别为三级的有4天,设其编号为,,,;
样本中空气质量级别为四级的有2天,设其编号为,,
则基本事件有:
,,,,,,,,,,,,,,共15个.
其中至少有一天空气质量类别为中度污染的情况有:
,,,,,,,,
共9个.
所以至少有一天空气质量类别为中度污染的概率为. ……………9分
(19)解:(Ⅰ)因为定义域为的函数是奇函数,
所以. ……………………………………2分
(Ⅱ)因为当时,,
所以.
又因为函数是奇函数,所以.
所以.
综上, ……………………………………6分
(Ⅲ)由得.
因为是奇函数, 所以.又在上是减函数,所以.
即对任意恒成立.
【方法一】令,则.由,解得.
【方法二】即对任意恒成立. 令,
则
故实数的取值范围为. ……………………………………10分
(20)解:(Ⅰ)由题设,当时,,
所以.
因为函数为二阶伸缩函数,
所以对任意,都有.
所以. ……………………………4分
(Ⅱ)当()时,.
由为三阶伸缩函数,有.
注意到时,.
所以.
令,解得或,它们均不在内. ……7分
所以函数在上无零点. ……………………………8分
(Ⅲ) 由题设,若函数为阶伸缩函数,有,
且当时, 的取值范围是.
所以当时,.
因为, 所以.
所以当时,.
当时,即,
则使,
,即,
.
又,
,即.
因为,
所以在()上的取值范围是.……………12分
同课章节目录
