2025届高考数学复习专题 ★★泰勒公式在高中数学中的应用 课件(共17张PPT)
文档属性
| 名称 | 2025届高考数学复习专题 ★★泰勒公式在高中数学中的应用 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 08:44:43 | ||
图片预览





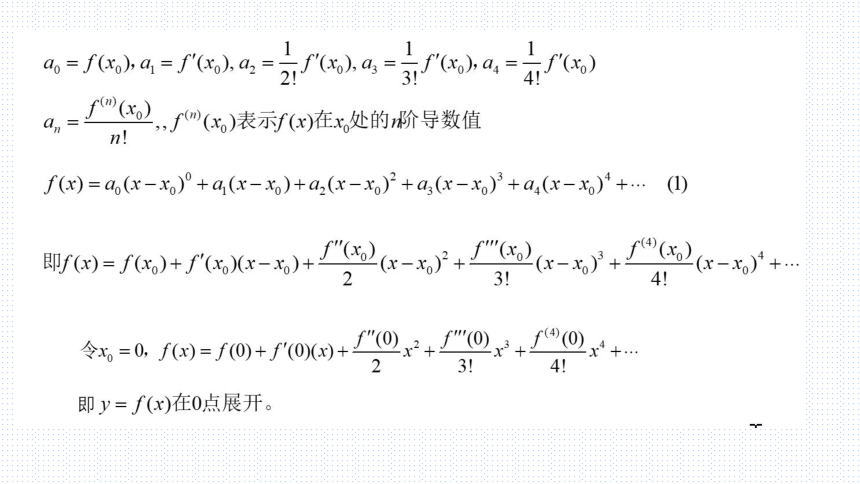
文档简介
(共17张PPT)
泰勒公式
2025届高考数学复习专题 ★★
泰勒公式
什么是泰勒公式
泰勒公式的应用:
@证明不等式
@求参数范围
@比较大小
什么是泰勒公式
泰勒公式,是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件,泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。
泰勒公式得名于英国数学家布鲁克·泰勒,他在1712年的一封信里首次叙述了这个公式。泰勒公式是为了研究复杂函数性质时经常使用的近似方法之一,也是函数微分学的一项重要应用内容。
泰勒公式
泰勒公式产生背景:
常见函数的泰勒展开式
泰勒展开式 记忆方法
切线放缩
特别地,有
泰勒公式的应用:
@证明不等式
泰勒公式的应用:
@求参数范围
泰勒公式的应用:
@求参数范围
泰勒公式的应用:
@求参数范围
站得更高,高山也矮小!
ciK
+
妆《
E
sinx
X
5
X
∑》
(2n+1)
n=
-10
5
5
10
a=7.426
×
口
0
●
10
-5
技术支持
世
desmos
pa-1
a
P=20+2W
axp
-b±V丽
.--20
a=1
N
1
15
⊙
a-=1
8
g(x)=In(x+1)
6
4
f(x)=泰勒公式(In(x+1),0a)
2
→
X
-8-6-4-2
246
输入
2
一、泰勒公式(泰勒中值定理)
1、设函数fx)在包含x的某区间(a,)内有n+1阶导数,则对任一x∈(@,),
有)=0+/6Xx-+2(x-2++626x-产+R⊙,其
21
中R份=包x-6)州,5是位于%与x之间的某个值。
(2+1)1
上面的表达式称为拉格朗日型余项。
2如果c=加,则R(训=a年k-m0x→,这时
织云0,即R)=o-八,这个表达式称为佩亚诺(Ren)型余项
3、若取0=0,则j)=f0+/0x+02++2+(,称
21
21
为麦克劳林公式。
最简单的函数,是多式项式函数
a(x-xo)'+a,(x-x)+a2(x-x)2+a3(x-xo)3+a4(x-xo)4+…
如果一个函数y=∫(x),可用上面的多项式函数来模拟,那就化复杂为简单,想想有多
美。其实,我们学过,y=f(x)在其上点(x,y)处的切线方程为
y=(x)+'(xo)(x-x),这就说明y=f(x)在x附近的曲线状态可以由其切线
y=∫(xo)+∫'(x(x-)来近似模拟(以直代曲)。
泰勒公式
2025届高考数学复习专题 ★★
泰勒公式
什么是泰勒公式
泰勒公式的应用:
@证明不等式
@求参数范围
@比较大小
什么是泰勒公式
泰勒公式,是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件,泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。
泰勒公式得名于英国数学家布鲁克·泰勒,他在1712年的一封信里首次叙述了这个公式。泰勒公式是为了研究复杂函数性质时经常使用的近似方法之一,也是函数微分学的一项重要应用内容。
泰勒公式
泰勒公式产生背景:
常见函数的泰勒展开式
泰勒展开式 记忆方法
切线放缩
特别地,有
泰勒公式的应用:
@证明不等式
泰勒公式的应用:
@求参数范围
泰勒公式的应用:
@求参数范围
泰勒公式的应用:
@求参数范围
站得更高,高山也矮小!
ciK
+
妆《
E
sinx
X
5
X
∑》
(2n+1)
n=
-10
5
5
10
a=7.426
×
口
0
●
10
-5
技术支持
世
desmos
pa-1
a
P=20+2W
axp
-b±V丽
.--20
a=1
N
1
15
⊙
a-=1
8
g(x)=In(x+1)
6
4
f(x)=泰勒公式(In(x+1),0a)
2
→
X
-8-6-4-2
246
输入
2
一、泰勒公式(泰勒中值定理)
1、设函数fx)在包含x的某区间(a,)内有n+1阶导数,则对任一x∈(@,),
有)=0+/6Xx-+2(x-2++626x-产+R⊙,其
21
中R份=包x-6)州,5是位于%与x之间的某个值。
(2+1)1
上面的表达式称为拉格朗日型余项。
2如果c=加,则R(训=a年k-m0x→,这时
织云0,即R)=o-八,这个表达式称为佩亚诺(Ren)型余项
3、若取0=0,则j)=f0+/0x+02++2+(,称
21
21
为麦克劳林公式。
最简单的函数,是多式项式函数
a(x-xo)'+a,(x-x)+a2(x-x)2+a3(x-xo)3+a4(x-xo)4+…
如果一个函数y=∫(x),可用上面的多项式函数来模拟,那就化复杂为简单,想想有多
美。其实,我们学过,y=f(x)在其上点(x,y)处的切线方程为
y=(x)+'(xo)(x-x),这就说明y=f(x)在x附近的曲线状态可以由其切线
y=∫(xo)+∫'(x(x-)来近似模拟(以直代曲)。
同课章节目录
