第十九章 一次函数(11类题型突破)(含解析)
文档属性
| 名称 | 第十九章 一次函数(11类题型突破)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览




文档简介
第十九章 一次函数(11类题型突破)
题型一 对函数概念的理解
例题:(2023上·浙江·八年级专题练习)下列图象中,y不是x的函数图象的是( )
A. B.
C. D.
变式训练
1.(2022下·广东广州·八年级广州市第七十五中学校考期中)下列各曲线中,表示y是x的函数的是( )
A. B.
C. D.
2.(2023上·安徽蚌埠·八年级统考阶段练习)下列图象中,表示y是x的函数的是( )
A. B.
C. D.
题型二 用表格/表达式/图象表示变量之间的关系
例题:(2023上·江苏盐城·八年级校联考阶段练习)某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟元)和B套餐(月租费0元,通话费每分钟元)两种,设A套餐每月话费为(元),B套餐每月话费(元),月通话时间为x分钟.
(1)直接写出与x,与x的函数关系式;
(2)如果某用户使用A套餐本月缴费50元,求他本月的通话时间?
(3)如果某用户这个月的通话时间为280分钟时,选择哪种套餐更划算?
变式训练
1.(2023上·广东佛山·八年级校考阶段练习)在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)当所挂重物为时,弹簧有多长?不挂重物呢?
(2)请写出弹簧长度y与所挂物体质量x之间的函数关系式;当重物为时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
2.(2022下·福建漳州·七年级福建省诏安县第二实验中学校考期中)如图,是骆驼的体温随时间变化而变化的的关系图,据图回答下列问题:
(1)一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
(3)在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?
(4)A点表示的是什么?
3.(2023上·河南焦作·八年级统考期中)新学期,两摞规格相同准备发放的课本整齐地叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(1)若(本)表示课本数,表示整齐叠放在桌面上的课本距离地面的高度,则是的一次函数,请求出关于的函数表达式;
(2)桌面上有55本与题(1)中相同的课本,整齐叠放成一摞,求这些数学课本距离地面的高度;
(3)小马说:如果把我班60名学生的这种课本整齐叠成一摞放在地面上,则它离地面有高.你认为小马的说法正确吗?请说明理由.
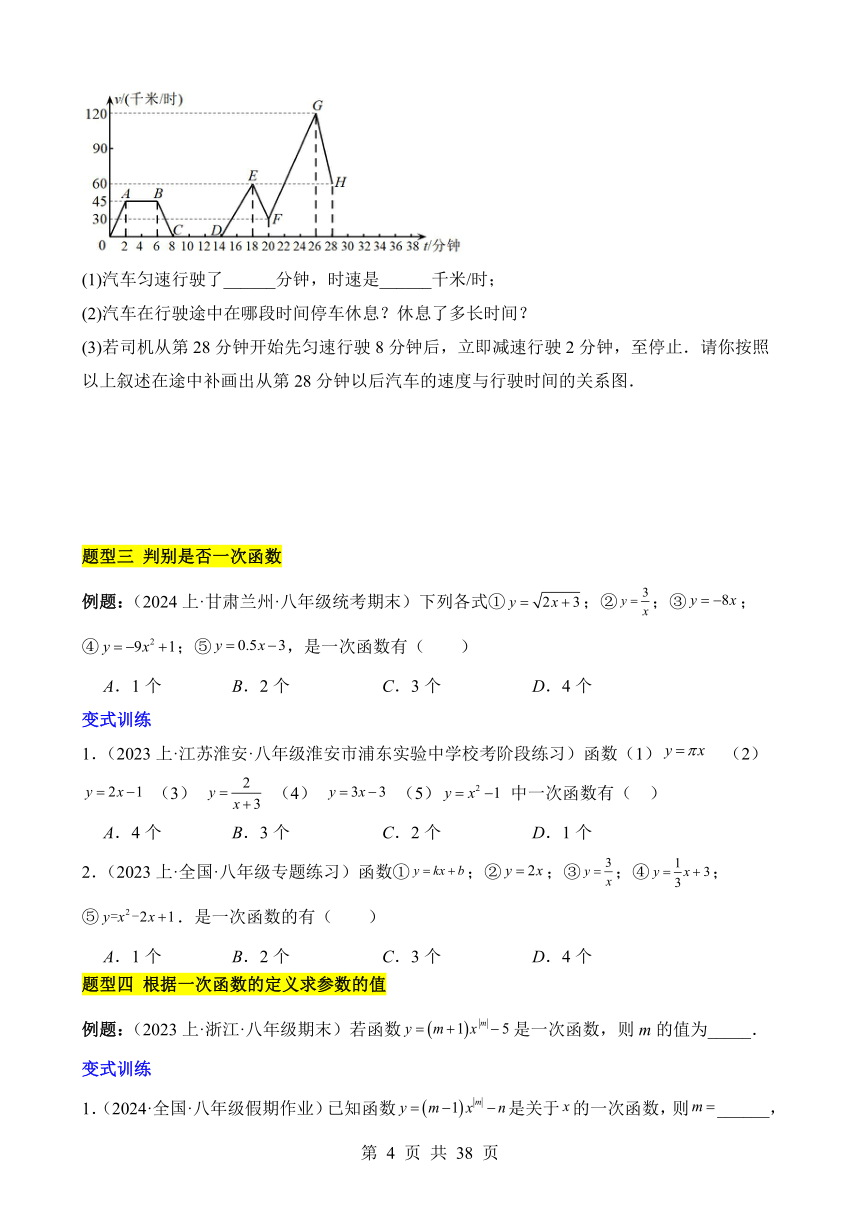
4.(2023下·陕西西安·七年级西安市第二十六中学校考阶段练习)如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车匀速行驶了______分钟,时速是______千米/时;
(2)汽车在行驶途中在哪段时间停车休息?休息了多长时间?
(3)若司机从第28分钟开始先匀速行驶8分钟后,立即减速行驶2分钟,至停止.请你按照以上叙述在途中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
题型三 判别是否一次函数
例题:(2024上·甘肃兰州·八年级统考期末)下列各式①;②;③;④;⑤,是一次函数有( )
A.1个 B.2个 C.3个 D.4个
变式训练
1.(2023上·江苏淮安·八年级淮安市浦东实验中学校考阶段练习)函数(1) (2) (3) (4) (5) 中一次函数有( )
A.4个 B.3个 C.2个 D.1个
2.(2023上·全国·八年级专题练习)函数①;②;③;④;⑤.是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
题型四 根据一次函数的定义求参数的值
例题:(2023上·浙江·八年级期末)若函数是一次函数,则m的值为_____.
变式训练
1.(2024·全国·八年级假期作业)已知函数是关于的一次函数,则______,若该函数是正比例函数,则______,______.
2.(2022上·四川成都·八年级成都嘉祥外国语学校校考期末)已知函数是关于x的一次函数,则_____.
题型五 画一次函数的图象
例题:(2023上·安徽滁州·八年级校考阶段练习)已知函数.
(1)请在所给的平面直角坐标系中画出该函数的图象.
(2)结合所画图象,分别求出在函数图象上满足下列条件的点的坐标:
①横坐标是;
②和轴的距离是2个单位长度.
变式训练
1.(2023上·福建漳州·八年级福建省漳州第一中学校考阶段练习)已知,一次函数的图像分别与轴,轴交于点A,B.
(1)请直接写出两点坐标:A:__________,B:__________;
(2)在直角坐标系中画出函数图象(不用列表,直接描点、连线);
(3)点是一次函数上一动点,则的最小值为___________.
2.(2023上·宁夏银川·八年级银川唐徕回民中学校考期中)已知函数回答下列问题:
(1)画出函数的图象;当_________时,.
(2)设直线与轴交于点,与轴交于点,求出的面积.
(3)直线上是否存在一点(与不重合),使的面积等于8?若存在,求出点的坐标;若不存在,请说明理由.
题型六 一次函数的图象和性质
例题:(2023上·广东深圳·八年级校考期中)下列关于函数的结论中,错误的是( )
A.图象经过点
B.点,在该函数图象上,若,则
C.将函数图象向下平移2个单位长度后,经过点
D.图象不经过第四象限
变式训练
1.(2023下·广西南宁·八年级校考阶段练习)对于一次函数,下列说法正确的是( )
A.图象不经过第三象限
B.当时,
C.图象由直线向上平移2个单位长度得到
D.图象与x轴交于点
2.(2023上·安徽六安·八年级校考阶段练习)一次函数,下列结论错误的是( )
A.若两点A(),B()在该函数图象上,且,则
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到的图象
D.函数的图象与轴的交点坐标是
题型七 根据一次函数经过的象限求参数问题
例题:(2023上·山东青岛·八年级统考期中)一次函数的图象不经过第________象限.
变式训练
1.(2023上·内蒙古包头·八年级校考期中)一次函数的图象不经过第三象限,则m的取值范围是____.
2.(2024上·陕西西安·八年级西安市第二十六中学校联考期末)已知直线经过第二、四象限,则直线不经过第______象限.
题型八 根据一次函数的增减性求参数问题
例题:(2024上·陕西西安·八年级统考期末)在一次函数中,随的增大而减小,则m的值可以是______.(写出一个即可)
变式训练
1.(2023上·江苏徐州·八年级校考阶段练习)一次函数中,若y随x的增大而增大,则m的取值范围是___.
2.(2024上·江苏·八年级泰州市姜堰区第四中学校考周测)若一次函数 的函数值随x的增大而增大,且函数的图像不经过第二象限,则k的取值范围是 _________
题型九 一次函数的图象与坐标轴的交点问题
例题:(2023上·陕西咸阳·八年级校考阶段练习)函数的图象与轴的交点是________.
变式训练
1.(2023上·海南海口·九年级海南中学校考阶段练习)一次函数与轴交点的坐标为________,与轴交点的坐标为________.
2.(2023上·福建福州·八年级福建省福州格致中学校考期中)直线与x轴的交点坐标是_____;与y轴的交点坐标是_____;与坐标轴围成的三角形面积为_____.
题型十 用待定系数法求一次函数的表达式
例题:(2023上·江苏扬州·八年级扬州教育学院附中校考阶段练习)已知一次函数.当时,;当时.
(1)求该一次函数的表达式;
(2)当时,求x的值.
变式训练
1.(2024上·安徽合肥·八年级统考期末)已知一次函数的图象与直线平行,且与轴交于点,求该一次函数的表达式.
2.(2024上·陕西榆林·八年级校考期末)如图,一次函数的图象与轴,轴分别交于点,且经过点.
(1)求一次函数的表达式.
(2)求的长.
3.(2024上·安徽合肥·八年级统考期末)已知与成正比例,当时,.
(1)求y与x之间的关系式;
(2)求(1)中的函数图象与坐标轴围成的三角形的面积.
题型十一 一次函数与三角形的面积问题
例题:(2023春·河南郑州·八年级郑州外国语中学校考期末)如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点、,且点的横坐标为1.
(1)点的坐标是______直线的解析式是_______
(2)连接,求的面积.
(3)点是直线上一点(不与点重合),设点的横坐标为,的面积为,请直接写出与之间的关系式.
变式训练
1.(2023秋·陕西西安·八年级校考期末)已知一次函数与的图像都过点,且与y轴分别交于点B,C.
(1)求m,n的值;
(2)求的面积.
2.(2023·江苏·八年级泰州市姜堰区第四中学校考期末)已知,一次函数的图像与x轴、y轴分别相交于A、B两点,点P的坐标为.
(1)若一次函数的图像经过点P,求m的值;
(2)若点P在x轴上,求的面积.
3.(2022秋·山东东营·七年级统考期末)已知某一次函数的图象经过点,且与正比例函数的图象相交于点,求:
(1)的值;
(2)一次函数y与x的函数解析式;
(3)这两个函数图象与轴所围成的三角形的面积.
第十九章 一次函数(11类题型突破)
答案全解全析
题型一 对函数概念的理解
例题:(2023上·浙江·八年级专题练习)下列图象中,y不是x的函数图象的是( )
A. B.
C. D.
【答案】C
【分析】本题考查了函数的概念,根据函数的概念:对于自变量x的每一个值,因变量y都有唯一的值与它对应,即可解答.
【详解】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故B不符合题意;
C、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故C符合题意;
D、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故D不符合题意.
故选:C.
变式训练
1.(2022下·广东广州·八年级广州市第七十五中学校考期中)下列各曲线中,表示y是x的函数的是( )
A. B.
C. D.
【答案】D
【分析】主要考查了函数的定义.对于自变量的任何值,都有唯一的值与之相对应,据此逐一判断即可求出答案.注意函数的意义反映在图象上简单的判断方法是:作垂直轴的直线在左右平移的过程中与函数图象只会有一个交点,正确理解定义是解题关键.
【详解】解:A.对于自变量的任何值,有时有两个值与之相对应,故不是的函数,不符合题意,
B.对于自变量的任何值,有时有两个值与之相对应,故不是的函数,不符合题意,
C.对于自变量的任何值,有时有两个值与之相对应,故不是的函数,不符合题意,
D.对于自变量的任何值,都有唯一的值与之相对应,故是的函数,符合题意,
故选:D.
2.(2023上·安徽蚌埠·八年级统考阶段练习)下列图象中,表示y是x的函数的是( )
A. B.
C. D.
【答案】B
【分析】在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,由此即可判断.
【详解】解:A、 表示y不是x的函数,该选项不符合题意的;
B、 表示y是x的函数,该选项是符合题意的;
C、 表示 y不是x的函数,该选项不符合题意的;
D、 表示 y不是x的函数,该选项不符合题意的;
故选:B.
【点睛】本题考查函数的概念,关键是掌握函数的定义.
题型二 用表格/表达式/图象表示变量之间的关系
例题:(2023上·江苏盐城·八年级校联考阶段练习)某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟元)和B套餐(月租费0元,通话费每分钟元)两种,设A套餐每月话费为(元),B套餐每月话费(元),月通话时间为x分钟.
(1)直接写出与x,与x的函数关系式;
(2)如果某用户使用A套餐本月缴费50元,求他本月的通话时间?
(3)如果某用户这个月的通话时间为280分钟时,选择哪种套餐更划算?
【答案】(1),
(2)他本月的通话时间为分钟
(3)通话时间为280分钟时,选择套餐更划算
【分析】本题主要考查了列函数关系和求函数值和自变量的值,根据题意正确列出关系式是解题关键.
(1)根据题意列函数关系式即可;
(2)根据题意可知,,求出的值即可;
(3)分别求出时,和的值,比较大小即可.
【详解】(1)解:A套餐:月租费15元,通话费每分钟元,
,
B套餐:月租费0元,通话费每分钟元,
;
(2)解:该手机用户使用A套餐且本月缴费50元,
,
解得:,
他本月的通话时间为分钟;
(3)解:当时,,,
,
∴通话时间为280分钟时,选择套餐更划算.
变式训练
1.(2023上·广东佛山·八年级校考阶段练习)在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)当所挂重物为时,弹簧有多长?不挂重物呢?
(2)请写出弹簧长度y与所挂物体质量x之间的函数关系式;当重物为时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
【答案】(1)当所挂重物为时,弹簧有,不挂重物时,弹簧有
(2),当重物为时,弹簧有
【分析】本题考查考查了函数的表示方法,明确变量及变量之间的关系是解好本题的关键.
(1)由表格数据直接求解即可;
(2)根据表格数据,所挂物体质量每增加,弹簧长度增加,据此得到函数关系式即可.
【详解】(1)解:由表格知,当时,,当时,,
答:当所挂重物为时,弹簧有,不挂重物时,弹簧有;
(2)解:∵所挂物体质量每增加,弹簧长度增加,
∴弹簧长度y与所挂物体质量x之间的函数关系式,
当时,,即当重物为时,弹簧有.
2.(2022下·福建漳州·七年级福建省诏安县第二实验中学校考期中)如图,是骆驼的体温随时间变化而变化的的关系图,据图回答下列问题:
(1)一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
(3)在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?
(4)A点表示的是什么?
【答案】(1)35℃~40℃;12小时
(2)3℃
(3)4时到16时体温上升;0时到4时,16时到24时体温下降
(4)12时,骆驼的体温为39℃
【分析】观察0时到24时,骆驼的体温变化,进行解答即可.
【详解】(1)解:由图可知,最低体温为,最高体温为,
∴骆驼体温的变化范围为;
∵,
∴从最低体温上升到最高体温需要12小时.
(2)解:由图可知16时体温为,24时体温为
∵
∴骆驼体温下降了.
(3)解:由图可知,在4时到16时,骆驼体温上升;在0时到4时,16时到24时,骆驼体温下降.
(4)解:点表示,在12时,骆驼的体温为.
【点睛】本题考查了图象表示变量间的关系.解题的关键在于从图中获取正确的信息.
3.(2023上·河南焦作·八年级统考期中)新学期,两摞规格相同准备发放的课本整齐地叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(1)若(本)表示课本数,表示整齐叠放在桌面上的课本距离地面的高度,则是的一次函数,请求出关于的函数表达式;
(2)桌面上有55本与题(1)中相同的课本,整齐叠放成一摞,求这些数学课本距离地面的高度;
(3)小马说:如果把我班60名学生的这种课本整齐叠成一摞放在地面上,则它离地面有高.你认为小马的说法正确吗?请说明理由.
【答案】(1)
(2)这些课本距离地面的高度为
(3)小马的说法错误,理由见解析
【分析】本题主要考查了列代数式,求函数值:
(1)求出一本课本的高度,讲台高度,即可;
(2)将代入(1)中的解析式,求函数值即可;
(3)求出60本课本整齐叠成一摞放在地面上离地面的高度,即可求解.
【详解】(1)解:一本课本的高度,
讲台高度,
关于的函数表达式为:;
(2)解:当时,;
故这些课本距离地面的高度为;
(3)解:如果把这种课本整齐叠成一摞放在地面上,则它离地面的高度为,
,
小马的说法错误.
4.(2023下·陕西西安·七年级西安市第二十六中学校考阶段练习)如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车匀速行驶了______分钟,时速是______千米/时;
(2)汽车在行驶途中在哪段时间停车休息?休息了多长时间?
(3)若司机从第28分钟开始先匀速行驶8分钟后,立即减速行驶2分钟,至停止.请你按照以上叙述在途中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
【答案】(1)4,45
(2)汽车在行驶途中,在分钟这个时间段停车休息,休息了6分钟
(3)见解析
【分析】(1)直接由图象知汽车在段匀速行驶,进而可得结论;
(2)直接由图知,汽车在段的速度为0,进而可求解;
(3)根据题中描述补画图象即可.
【详解】(1)解:由图知,汽车匀速行驶了(分钟),时速是45千米/时,
故答案为:4,45;
(2)解:由图可知,汽车在段的速度为0,所以汽车在行驶途中,在分钟这个时间段停车休息,休息了(分钟).
(3)解:如图所示:
【点睛】本题考查用图象表示变量间的关系,理解题意,从图象上获取所需信息是解答的关键.
题型三 判别是否一次函数
例题:(2024上·甘肃兰州·八年级统考期末)下列各式①;②;③;④;⑤,是一次函数有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查了一次函数的定义,一般地,形如,(k为常数,)的函数叫做一次函数.根据定义分析即可.
【详解】解:①的右边不是整式,不是一次函数;
②的右边不是整式,不是一次函数;;
③是一次函数;
④的自变量的次数是2,不是一次函数;
⑤是一次函数.
故选B.
变式训练
1.(2023上·江苏淮安·八年级淮安市浦东实验中学校考阶段练习)函数(1) (2) (3) (4) (5) 中一次函数有 ( )
A.4个 B.3个 C.2个 D.1个
【答案】B
【分析】本题考查的是一次函数的定义,解决本题的关键是明确一次函数的定义,一般地,形如 (,k,b是常数)的函数,叫做一次函数.
利用一次函数的定义分析得出即可.
【详解】解:(1)是一次函数,符合题意;
(2)是一次函数,符合题意;
(3)中不是整式,不是一次函数,不符合题意;
(4)是一次函数,符合题意;
(5)的自变量的次数是2,不是一次函数,不符合题意;
故是一次函数的有3个.
故选:B.
2.(2023上·全国·八年级专题练习)函数①;②;③;④;⑤.是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查了一次函数的定义,形如的函数,熟练掌握定义是解题的关键.
【详解】解:①,当时,不是一次函数;
②是一次函数;
③不是一次函数;
④是一次函数;
⑤不是一次函数;
所以是一次函数的有2个.
故选:B.
题型四 根据一次函数的定义求参数的值
例题:(2023上·浙江·八年级期末)若函数是一次函数,则m的值为_____.
【答案】1
【分析】本题考查了一次函数的定义,一般地,形如,(k为常数,)的函数叫做一次函数.由一次函数的定义可知且,从而可求得m的值.
【详解】解:∵是一次函数,
∴且,
解得且,
所以,
故答案为:1.
变式训练
1.(2024·全国·八年级假期作业)已知函数是关于的一次函数,则______,若该函数是正比例函数,则______,______.
【答案】 0
【分析】本题考查了正比例函数的定义:一般地,形如(k是常数,)的函数叫做正比例函数,其中k叫做比例系数.一次函数的定义:一般地,形如(,k、b是常数)的函数,叫做一次函数.根据一次函数的定义,正比例函数的定义求解即可.
【详解】解:当函数是关于x的一次函数时,,且,解得;
当函数是关于x的正比例函数时,,,且,解得,.
故答案为:,,0.
2.(2022上·四川成都·八年级成都嘉祥外国语学校校考期末)已知函数是关于x的一次函数,则_____.
【答案】
【分析】该题主要考查了一次函数的定义,解答的关键是熟悉一次函数的定义;
根据函数是一次函数,得出,进行解答即可;
【详解】解:根据题意得:,
解得:.
故答案为:.
题型五 画一次函数的图象
例题:(2023上·安徽滁州·八年级校考阶段练习)已知函数.
(1)请在所给的平面直角坐标系中画出该函数的图象.
(2)结合所画图象,分别求出在函数图象上满足下列条件的点的坐标:
①横坐标是;
②和轴的距离是2个单位长度.
【答案】(1)见解析
(2)①横坐标是的点是;②和轴的距离是2个单位长度的点的坐标为或
【分析】本题考查了画一次函数的图象,一次函数的性质,采用数形结合的思想是解此题的关键.
(1)根据解析式先求出函数与轴、轴的交点,即可画出图象;
(2)①将代入解析式进行计算求出的值即可;②由和轴的距离是2个单位长度得出或,分别代入计算,求出的值即可.
【详解】(1)解:在函数中,
当时,,则过,
当时,,解得:,则过,
画出该函数图象如图所示:
;
(2)解:①当时,,
横坐标是的点是;
②和轴的距离是2个单位长度,
或,
当时,,解得:,此时点的坐标为,
当时,,解得:,此时点的坐标为,
综上所述,和轴的距离是2个单位长度的点的坐标为或.
变式训练
1.(2023上·福建漳州·八年级福建省漳州第一中学校考阶段练习)已知,一次函数的图像分别与轴,轴交于点A,B.
(1)请直接写出两点坐标:A:__________,B:__________;
(2)在直角坐标系中画出函数图象(不用列表,直接描点、连线);
(3)点是一次函数上一动点,则的最小值为___________.
【答案】(1)
(2)见解析
(3)
【分析】本题考查了一次函数的图象,一次函数与坐标轴交点问题,勾股定理.
(1)根据题目即可求出A、B两点的坐标;
(2)根据(1)中A、B两点的坐标即可画出函数图象;
(3)先利用勾股定理求出,当与一次函数垂直时,有最小值,再根据等面积法,即可求出的最短距离.
【详解】(1)解:∵一次函数的图象分别与x轴、y轴交于点A、B,
∴当时,,
当时,,
∴A、B两点的坐标为,
故答案为:;
(2)解:由(1)得:A、B两点的坐标为,
∴函数图象如图所示:
(3)解:如图所示,当与一次函数垂直时,有最小值,
此时,,
,
,
,
,
故答案为:.
2.(2023上·宁夏银川·八年级银川唐徕回民中学校考期中)已知函数回答下列问题:
(1)画出函数的图象;当_________时,.
(2)设直线与轴交于点,与轴交于点,求出的面积.
(3)直线上是否存在一点(与不重合),使的面积等于8?若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1)图象见解析,
(2)4
(3)存在,点C的坐标为或
【分析】本题考查了一次函数图象上点的坐标特征、一次函数的图象以及一次函数的性质,利用一次函数图象上点的坐标特征,求出点A,B的坐标并画出函数图象是解题的关键.
(1)利用一次函数图象上点的坐标特征,描点、连线,即可画出一次函数的图象,观察函数图象,即可得出当时,;
(2)由点A,B的坐标可得出,的长,再利用三角形的面积计算公式,即可求出的面积;
(3)设点的纵坐标为a,根据题意可得:,得出,再分别求出C点的坐标即可.
【详解】(1)解:当时,,
当时,,
解得:,
描点、连线,画出函数图象,如图所示.
由图象可知:当时,.
故答案为:;
(2)解:∵点A的坐标为,点B的坐标为,
∴,,
的面积为;
(3)存在点,使的面积等于8,理由如下:
设点的纵坐标为a,
根据题意可得:,
解得:,
当时,,解得:,
当时,,解得:,
所以点C的坐标为:或.
题型六 一次函数的图象和性质
例题:(2023上·广东深圳·八年级校考期中)下列关于函数的结论中,错误的是( )
A.图象经过点
B.点,在该函数图象上,若,则
C.将函数图象向下平移2个单位长度后,经过点
D.图象不经过第四象限
【答案】C
【分析】本题考查的是一次函数的性质,一次函数图象的平移,根据一次函数图象上点的坐标特点可判断A,根据一次函数的增减性可判断B,根据一次函数图象的平移可判断C,根据一次函数系数与经过的象限的关系可判断D,熟记一次函数的性质是解本题的关键.
【详解】解:A、当时,,故图象经过点,故本选项正确,不合题意;
B、函数中,,
随的增大而增大,
∵,
,故本选项正确,不合题意;
C、根据平移的规律,函数的图象向下平移2个单位长度得解析式为,所以当时,,则图象经过点,故本选项错误,符合题意;
D、,,,函数经过第一,二,三象限,不经过第四象限,故本选项正确,不符合题意.
故选:C.
变式训练
1.(2023下·广西南宁·八年级校考阶段练习)对于一次函数,下列说法正确的是( )
A.图象不经过第三象限
B.当时,
C.图象由直线向上平移2个单位长度得到
D.图象与x轴交于点
【答案】C
【分析】根据一次函数的图象与性质即可解答.
【详解】解:∵一次函数解析式为,
∴图象经过第一、二、三象限,故A不符合题意;
当时,,故B不符合题意;
直线向上平移2个单位得到的新解析式为,故C符合题意;
对于,令,则,
∴图象与x轴交于点,故D不符合题意.
故选C.
【点睛】本题考查一次函数的图象与性质.熟练掌握一次函数的图象与性质是解题关键.
2.(2023上·安徽六安·八年级校考阶段练习)一次函数,下列结论错误的是( )
A.若两点A(),B()在该函数图象上,且,则
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到的图象
D.函数的图象与轴的交点坐标是
【答案】D
【分析】分别根据一次函数的性质及函数图象平移的法则进行解答即可.
【详解】A、因为一次函数中,因此函数值随x的增大而减小,故A选项正确;
B、因为一次函数中,,因此此函数的图象经过一、二、四象限,不经过第三象限,故B选项正确;
C、由“上加下减”的原则可知,函数的图象向下平移4个单位长度得的图象,故C选项正确;
D、令,则,因此函数的图象与x轴的交点坐标是,故D选项错误.
故选:D.
【点睛】本题考查的是一次函数的性质及一次函数的图象与几何变换,熟知一次函数的性质及函数图象平移的法则是解答此题的关键.
题型七 根据一次函数经过的象限求参数问题
例题:(2023上·山东青岛·八年级统考期中)一次函数的图象不经过第________象限.
【答案】四/4
【分析】本题考查一次函数解析式及其性质,根据一次函数的解析式和一次函数的性质,可以得到即可得出该函数的图象经过哪几个象限,不经过哪个象限.
【详解】解:∵一次函数,,
∴一次函数经过一、二、三象限,不经过第四象限,
故答案为:四.
变式训练
1.(2023上·内蒙古包头·八年级校考期中)一次函数的图象不经过第三象限,则m的取值范围是____.
【答案】/
【分析】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线所在的位置与k、b的符号有直接的关系. 时,直线必经过一、三象限.时,直线必经过二、四象限.时,直线与y轴正半轴相交.时,直线过原点;时,直线与y轴负半轴相交.
【详解】解:∵一次函数的图象不经过第三象限,
∴,
解得:,
故答案为:.
2.(2024上·陕西西安·八年级西安市第二十六中学校联考期末)已知直线经过第二、四象限,则直线不经过第______象限.
【答案】三
【分析】本题考查正比例函数的性质和一次函数的性质,先利用正比例函数的性质得到,然后根据一次函数的性质求解即可.熟练掌握相关函数的性质是解题的关键.
【详解】解:∵直线经过第二、四象限,
∴,
∴,
又∵,
∴直线经过第一、二、四象限,
即直线不经过第三象限.
故答案为:三.
题型八 根据一次函数的增减性求参数问题
例题:(2024上·陕西西安·八年级统考期末)在一次函数中,随的增大而减小,则m的值可以是______.(写出一个即可)
【答案】(答案不唯一)
【分析】本题考查一次函数的性质,根据随的增大而减小,则,据此写出的值即可,答案不唯一.解题的关键是掌握:一次函数中,若,则随的增大而增大;若,则随的增大而减小,反过来也成立.
【详解】解:∵在一次函数中,随的增大而减小,
∴,
不妨设,
∴的值可以是.
故答案为:.
变式训练
1.(2023上·江苏徐州·八年级校考阶段练习)一次函数中,若y随x的增大而增大,则m的取值范围是___.
【答案】/
【分析】本题考查了一次函数图象与系数的关系.在一次函数中,函数值y随x的增大而减小;函数值y随x的增大而增大.当时,直线中y的值随x的增大而增大.通过解不等式来求m的取值范围.
【详解】解:∵直线中y的值随x的增大而减小,
,
解得,.
故答案为:.
2.(2024上·江苏·八年级泰州市姜堰区第四中学校考周测)若一次函数 的函数值随x的增大而增大,且函数的图像不经过第二象限,则k的取值范围是 _________
【答案】
【分析】本题考查了一次函数的性质,熟练掌握当k大于零时,函数值随x的增大而增大;图像与y轴的交点不高于原点,列式计算即可.
【详解】∵一次函数 的函数值随x的增大而增大,且函数的图像不经过第二象限,
∴,
解得,
故答案为:.
题型九 一次函数的图象与坐标轴的交点问题
例题:(2023上·陕西咸阳·八年级校考阶段练习)函数的图象与轴的交点是________.
【答案】
【分析】本题考查了一次函数的图像及性质,熟记“一次函数与轴有交点时函数值y为0”
【详解】解:当与轴有交点时,,
有,
解得:.
故答案为:.
变式训练
1.(2023上·海南海口·九年级海南中学校考阶段练习)一次函数与轴交点的坐标为________,与轴交点的坐标为________.
【答案】
【分析】根据一次函数解析式为,求出当时,的值,得出与轴交点的坐标;求出当时,的值,得出与轴交点的坐标即可.
【详解】解:∵一次函数解析式为,
∴当时,则,
解得:,
当时,则,
∴一次函数与轴交点的坐标为,与轴交点的坐标为.
故答案为:;.
【点睛】本题考查了一次函数图象与坐标轴的交点问题,明白坐标轴上点的坐标特点是解题的关键.
2.(2023上·福建福州·八年级福建省福州格致中学校考期中)直线与x轴的交点坐标是_____;与y轴的交点坐标是_____;与坐标轴围成的三角形面积为_____.
【答案】
【分析】分别令,,求出直线与x轴的交点坐标是;与y轴的交点坐标是,即可求解.
【详解】解:令,,
令,,
解得:,
∴直线与x轴的交点坐标是;与y轴的交点坐标是,
∴与坐标轴围成的三角形面积为.
故答案为:;;
【点睛】本题考查的是一次函数图象上点的坐标特点,熟知一次函数函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.另外要记住一次函数图象与坐标轴所围成的三角形的面积计算公式.
题型十 用待定系数法求一次函数的表达式
例题:(2023上·江苏扬州·八年级扬州教育学院附中校考阶段练习)已知一次函数.当时,;当时.
(1)求该一次函数的表达式;
(2)当时,求x的值.
【答案】(1)
(2)
【分析】本题考查了待定系数法求一次函数解析式,已知函数值求自变量的取值等知识.
(1)利用待定系数法即可求解;
(2)把代入一次函数解析式得到,解方程即可求解.
【详解】(1)解:∵一次函数,当时,;当时,
∴,
∴,
∴一次函数的表达式为;
(2)解:当时,,
解得.
变式训练
1.(2024上·安徽合肥·八年级统考期末)已知一次函数的图象与直线平行,且与轴交于点,求该一次函数的表达式.
【答案】
【分析】本题考查了平面直角坐标系内两条平行直线的函数解析式的性质,平面直角坐标系内直线与轴的交点问题,熟知两直线平行则k相等是解题的关键.根据直线与直线平行得到k的值;再根据直线交轴于点得到b的值,进而得出函数的表达式.
【详解】解:一次函数的图象与直线平行,
,
将点代入中,可得
,
一次函数的表达式为:.
2.(2024上·陕西榆林·八年级校考期末)如图,一次函数的图象与轴,轴分别交于点,且经过点.
(1)求一次函数的表达式.
(2)求的长.
【答案】(1)
(2)10
【分析】本题考查了待定系数法求一次函数解析式,勾股定理;
(1)待定系数法求解析式即可求解;
(2)先求得点的坐标为,然后根据勾股定理,即可求解.
【详解】(1)解:由题意可得,解得.
一次函数的表达式为.
(2)令,则,
解得,
点的坐标为,
.
令,则,
点的坐标为,
.
.
3.(2024上·安徽合肥·八年级统考期末)已知与成正比例,当时,.
(1)求y与x之间的关系式;
(2)求(1)中的函数图象与坐标轴围成的三角形的面积.
【答案】(1)
(2)
【分析】本题考查待定系数法求一次函数解析式,一次函数与坐标轴交点问题;
(1)设,当时,,求出,即可求出与之间的函数表达式;
(2)求出直线与、轴交点的坐标,即可得到,的长,根据三角形的面积公式,即可求解.
【详解】(1)解:与成正比例
设,
当时,,
,
,
,
即
与之间的函数表达式是,
(2)设直线与、轴分别交于、两点,
当时,,当时,,
的坐标是,的坐标是,
,,
函数图象与坐标轴围成的三角形面积是.
题型十一 一次函数与三角形的面积问题
例题:(2023春·河南郑州·八年级郑州外国语中学校考期末)如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点、,且点的横坐标为1.
(1)点的坐标是______直线的解析式是_______
(2)连接,求的面积.
(3)点是直线上一点(不与点重合),设点的横坐标为,的面积为,请直接写出与之间的关系式.
【答案】(1);
(2)
(3)
【分析】(1)根据D点横坐标及得出纵坐标进而得出D点坐标;最后通过两点坐标得出一次函数解析式;
(2)根据各点坐标即三角形面积公式即可求出;
(3)分情况讨论,利用图形面积的和差以及三角形的面积公式列式求解即可;
【详解】(1)将代入函数得D点纵坐标为2,将点,代入得:,解得,
故解析式为:
故答案为: ;;
(2)
如图:点A的坐标为,,点C的坐标为,
∴
;
(3)①如图,点P在之间:
;
②点P在B点下方,如图:
;
③点P在D点的上面
;
综上所述:
【点睛】本题考查待定系数法求一次函数解析式,一次函数与坐标轴围成的图形的面积的求解,会分割图形面积是关键.
变式训练
1.(2023秋·陕西西安·八年级校考期末)已知一次函数与的图像都过点,且与y轴分别交于点B,C.
(1)求m,n的值;
(2)求的面积.
【答案】(1),;
(2)4
【分析】(1)直接把点代入解析式,即可求出答案;
(2)分别求出B,C两点的坐标,然后利用面积公式,即可求出答案.
【详解】(1)解:∵一次函数与的图像都过点,
∴把点分别代入,得
,,
∴,;
(2)解:由(1)可知,,,
∴,,
分别令,则
,,
∴点B的坐标为,点C的坐标为;
∴,
∴的面积为:;
【点睛】本题考查了一次函数的图像和性质,一次函数与坐标轴的交点坐标,解题的关键是熟练掌握一次函数的性质进行解题.
2.(2023·江苏·八年级泰州市姜堰区第四中学校考期末)已知,一次函数的图像与x轴、y轴分别相交于A、B两点,点P的坐标为.
(1)若一次函数的图像经过点P,求m的值;
(2)若点P在x轴上,求的面积.
【答案】(1)0
(2)9
【分析】(1)将点P坐标代入一次函数表达式中,即可求出m值;
(2)首先根据一次函数表达式求出点A和点B坐标,再根据点P在x轴,可得纵坐标为0,可求出m值,从而得到点P坐标,结合坐标可得的面积.
【详解】(1)解:将点P代入中,
得,
解得:;
(2)在中,令,则,令,则,
∴,,
∵点P在x轴上,
∴,
∴,即,
∴.
【点睛】本题考查了一次函数图像上的点,一次函数与坐标轴的交点问题,解题的关键是求出相应点的坐标.
3.(2022秋·山东东营·七年级统考期末)已知某一次函数的图象经过点,且与正比例函数的图象相交于点,求:
(1)的值;
(2)一次函数y与x的函数解析式;
(3)这两个函数图象与轴所围成的三角形的面积.
【答案】(1)
(2)
(3)
【分析】(1)把交点坐标代入正比例函数解析式中求出a的值;
(2)将两点的坐标代入中,利用待定系数法求出一次函数解析式;
(3)先求得与x轴的交点A的坐标,再根据三角形面积公式进行计算.
【详解】(1)解:∵点在正比例函数的图象上,
∴;
(2)解:设一次函数的解析式为,
∵经过点,点,
∴,
解得,
∴一次函数的解析式为;
(3)解:∵时,,
∴,
∴与x轴的交点A为,
∵,
∴.
【点睛】本题主要是考查了待定系数法求解一次函数表达式以及求解与坐标轴的面积,正确利用待定系数法求出一次函数表达式,合理确定坐标轴围成的三角形的底和高,这是解决本题的关键.
第 页 共 页
题型一 对函数概念的理解
例题:(2023上·浙江·八年级专题练习)下列图象中,y不是x的函数图象的是( )
A. B.
C. D.
变式训练
1.(2022下·广东广州·八年级广州市第七十五中学校考期中)下列各曲线中,表示y是x的函数的是( )
A. B.
C. D.
2.(2023上·安徽蚌埠·八年级统考阶段练习)下列图象中,表示y是x的函数的是( )
A. B.
C. D.
题型二 用表格/表达式/图象表示变量之间的关系
例题:(2023上·江苏盐城·八年级校联考阶段练习)某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟元)和B套餐(月租费0元,通话费每分钟元)两种,设A套餐每月话费为(元),B套餐每月话费(元),月通话时间为x分钟.
(1)直接写出与x,与x的函数关系式;
(2)如果某用户使用A套餐本月缴费50元,求他本月的通话时间?
(3)如果某用户这个月的通话时间为280分钟时,选择哪种套餐更划算?
变式训练
1.(2023上·广东佛山·八年级校考阶段练习)在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)当所挂重物为时,弹簧有多长?不挂重物呢?
(2)请写出弹簧长度y与所挂物体质量x之间的函数关系式;当重物为时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
2.(2022下·福建漳州·七年级福建省诏安县第二实验中学校考期中)如图,是骆驼的体温随时间变化而变化的的关系图,据图回答下列问题:
(1)一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
(3)在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?
(4)A点表示的是什么?
3.(2023上·河南焦作·八年级统考期中)新学期,两摞规格相同准备发放的课本整齐地叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(1)若(本)表示课本数,表示整齐叠放在桌面上的课本距离地面的高度,则是的一次函数,请求出关于的函数表达式;
(2)桌面上有55本与题(1)中相同的课本,整齐叠放成一摞,求这些数学课本距离地面的高度;
(3)小马说:如果把我班60名学生的这种课本整齐叠成一摞放在地面上,则它离地面有高.你认为小马的说法正确吗?请说明理由.
4.(2023下·陕西西安·七年级西安市第二十六中学校考阶段练习)如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车匀速行驶了______分钟,时速是______千米/时;
(2)汽车在行驶途中在哪段时间停车休息?休息了多长时间?
(3)若司机从第28分钟开始先匀速行驶8分钟后,立即减速行驶2分钟,至停止.请你按照以上叙述在途中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
题型三 判别是否一次函数
例题:(2024上·甘肃兰州·八年级统考期末)下列各式①;②;③;④;⑤,是一次函数有( )
A.1个 B.2个 C.3个 D.4个
变式训练
1.(2023上·江苏淮安·八年级淮安市浦东实验中学校考阶段练习)函数(1) (2) (3) (4) (5) 中一次函数有( )
A.4个 B.3个 C.2个 D.1个
2.(2023上·全国·八年级专题练习)函数①;②;③;④;⑤.是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
题型四 根据一次函数的定义求参数的值
例题:(2023上·浙江·八年级期末)若函数是一次函数,则m的值为_____.
变式训练
1.(2024·全国·八年级假期作业)已知函数是关于的一次函数,则______,若该函数是正比例函数,则______,______.
2.(2022上·四川成都·八年级成都嘉祥外国语学校校考期末)已知函数是关于x的一次函数,则_____.
题型五 画一次函数的图象
例题:(2023上·安徽滁州·八年级校考阶段练习)已知函数.
(1)请在所给的平面直角坐标系中画出该函数的图象.
(2)结合所画图象,分别求出在函数图象上满足下列条件的点的坐标:
①横坐标是;
②和轴的距离是2个单位长度.
变式训练
1.(2023上·福建漳州·八年级福建省漳州第一中学校考阶段练习)已知,一次函数的图像分别与轴,轴交于点A,B.
(1)请直接写出两点坐标:A:__________,B:__________;
(2)在直角坐标系中画出函数图象(不用列表,直接描点、连线);
(3)点是一次函数上一动点,则的最小值为___________.
2.(2023上·宁夏银川·八年级银川唐徕回民中学校考期中)已知函数回答下列问题:
(1)画出函数的图象;当_________时,.
(2)设直线与轴交于点,与轴交于点,求出的面积.
(3)直线上是否存在一点(与不重合),使的面积等于8?若存在,求出点的坐标;若不存在,请说明理由.
题型六 一次函数的图象和性质
例题:(2023上·广东深圳·八年级校考期中)下列关于函数的结论中,错误的是( )
A.图象经过点
B.点,在该函数图象上,若,则
C.将函数图象向下平移2个单位长度后,经过点
D.图象不经过第四象限
变式训练
1.(2023下·广西南宁·八年级校考阶段练习)对于一次函数,下列说法正确的是( )
A.图象不经过第三象限
B.当时,
C.图象由直线向上平移2个单位长度得到
D.图象与x轴交于点
2.(2023上·安徽六安·八年级校考阶段练习)一次函数,下列结论错误的是( )
A.若两点A(),B()在该函数图象上,且,则
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到的图象
D.函数的图象与轴的交点坐标是
题型七 根据一次函数经过的象限求参数问题
例题:(2023上·山东青岛·八年级统考期中)一次函数的图象不经过第________象限.
变式训练
1.(2023上·内蒙古包头·八年级校考期中)一次函数的图象不经过第三象限,则m的取值范围是____.
2.(2024上·陕西西安·八年级西安市第二十六中学校联考期末)已知直线经过第二、四象限,则直线不经过第______象限.
题型八 根据一次函数的增减性求参数问题
例题:(2024上·陕西西安·八年级统考期末)在一次函数中,随的增大而减小,则m的值可以是______.(写出一个即可)
变式训练
1.(2023上·江苏徐州·八年级校考阶段练习)一次函数中,若y随x的增大而增大,则m的取值范围是___.
2.(2024上·江苏·八年级泰州市姜堰区第四中学校考周测)若一次函数 的函数值随x的增大而增大,且函数的图像不经过第二象限,则k的取值范围是 _________
题型九 一次函数的图象与坐标轴的交点问题
例题:(2023上·陕西咸阳·八年级校考阶段练习)函数的图象与轴的交点是________.
变式训练
1.(2023上·海南海口·九年级海南中学校考阶段练习)一次函数与轴交点的坐标为________,与轴交点的坐标为________.
2.(2023上·福建福州·八年级福建省福州格致中学校考期中)直线与x轴的交点坐标是_____;与y轴的交点坐标是_____;与坐标轴围成的三角形面积为_____.
题型十 用待定系数法求一次函数的表达式
例题:(2023上·江苏扬州·八年级扬州教育学院附中校考阶段练习)已知一次函数.当时,;当时.
(1)求该一次函数的表达式;
(2)当时,求x的值.
变式训练
1.(2024上·安徽合肥·八年级统考期末)已知一次函数的图象与直线平行,且与轴交于点,求该一次函数的表达式.
2.(2024上·陕西榆林·八年级校考期末)如图,一次函数的图象与轴,轴分别交于点,且经过点.
(1)求一次函数的表达式.
(2)求的长.
3.(2024上·安徽合肥·八年级统考期末)已知与成正比例,当时,.
(1)求y与x之间的关系式;
(2)求(1)中的函数图象与坐标轴围成的三角形的面积.
题型十一 一次函数与三角形的面积问题
例题:(2023春·河南郑州·八年级郑州外国语中学校考期末)如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点、,且点的横坐标为1.
(1)点的坐标是______直线的解析式是_______
(2)连接,求的面积.
(3)点是直线上一点(不与点重合),设点的横坐标为,的面积为,请直接写出与之间的关系式.
变式训练
1.(2023秋·陕西西安·八年级校考期末)已知一次函数与的图像都过点,且与y轴分别交于点B,C.
(1)求m,n的值;
(2)求的面积.
2.(2023·江苏·八年级泰州市姜堰区第四中学校考期末)已知,一次函数的图像与x轴、y轴分别相交于A、B两点,点P的坐标为.
(1)若一次函数的图像经过点P,求m的值;
(2)若点P在x轴上,求的面积.
3.(2022秋·山东东营·七年级统考期末)已知某一次函数的图象经过点,且与正比例函数的图象相交于点,求:
(1)的值;
(2)一次函数y与x的函数解析式;
(3)这两个函数图象与轴所围成的三角形的面积.
第十九章 一次函数(11类题型突破)
答案全解全析
题型一 对函数概念的理解
例题:(2023上·浙江·八年级专题练习)下列图象中,y不是x的函数图象的是( )
A. B.
C. D.
【答案】C
【分析】本题考查了函数的概念,根据函数的概念:对于自变量x的每一个值,因变量y都有唯一的值与它对应,即可解答.
【详解】解:A、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A不符合题意;
B、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故B不符合题意;
C、对于自变量x的每一个值,因变量y不是都有唯一的值与它对应,所以y不是x的函数,故C符合题意;
D、对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故D不符合题意.
故选:C.
变式训练
1.(2022下·广东广州·八年级广州市第七十五中学校考期中)下列各曲线中,表示y是x的函数的是( )
A. B.
C. D.
【答案】D
【分析】主要考查了函数的定义.对于自变量的任何值,都有唯一的值与之相对应,据此逐一判断即可求出答案.注意函数的意义反映在图象上简单的判断方法是:作垂直轴的直线在左右平移的过程中与函数图象只会有一个交点,正确理解定义是解题关键.
【详解】解:A.对于自变量的任何值,有时有两个值与之相对应,故不是的函数,不符合题意,
B.对于自变量的任何值,有时有两个值与之相对应,故不是的函数,不符合题意,
C.对于自变量的任何值,有时有两个值与之相对应,故不是的函数,不符合题意,
D.对于自变量的任何值,都有唯一的值与之相对应,故是的函数,符合题意,
故选:D.
2.(2023上·安徽蚌埠·八年级统考阶段练习)下列图象中,表示y是x的函数的是( )
A. B.
C. D.
【答案】B
【分析】在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,由此即可判断.
【详解】解:A、 表示y不是x的函数,该选项不符合题意的;
B、 表示y是x的函数,该选项是符合题意的;
C、 表示 y不是x的函数,该选项不符合题意的;
D、 表示 y不是x的函数,该选项不符合题意的;
故选:B.
【点睛】本题考查函数的概念,关键是掌握函数的定义.
题型二 用表格/表达式/图象表示变量之间的关系
例题:(2023上·江苏盐城·八年级校联考阶段练习)某通讯公司手机话费收费有A套餐(月租费15元,通话费每分钟元)和B套餐(月租费0元,通话费每分钟元)两种,设A套餐每月话费为(元),B套餐每月话费(元),月通话时间为x分钟.
(1)直接写出与x,与x的函数关系式;
(2)如果某用户使用A套餐本月缴费50元,求他本月的通话时间?
(3)如果某用户这个月的通话时间为280分钟时,选择哪种套餐更划算?
【答案】(1),
(2)他本月的通话时间为分钟
(3)通话时间为280分钟时,选择套餐更划算
【分析】本题主要考查了列函数关系和求函数值和自变量的值,根据题意正确列出关系式是解题关键.
(1)根据题意列函数关系式即可;
(2)根据题意可知,,求出的值即可;
(3)分别求出时,和的值,比较大小即可.
【详解】(1)解:A套餐:月租费15元,通话费每分钟元,
,
B套餐:月租费0元,通话费每分钟元,
;
(2)解:该手机用户使用A套餐且本月缴费50元,
,
解得:,
他本月的通话时间为分钟;
(3)解:当时,,,
,
∴通话时间为280分钟时,选择套餐更划算.
变式训练
1.(2023上·广东佛山·八年级校考阶段练习)在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体质量x/kg 0 1 2 3 4 5
弹簧长度y/cm 18 20 22 24 26 28
(1)当所挂重物为时,弹簧有多长?不挂重物呢?
(2)请写出弹簧长度y与所挂物体质量x之间的函数关系式;当重物为时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
【答案】(1)当所挂重物为时,弹簧有,不挂重物时,弹簧有
(2),当重物为时,弹簧有
【分析】本题考查考查了函数的表示方法,明确变量及变量之间的关系是解好本题的关键.
(1)由表格数据直接求解即可;
(2)根据表格数据,所挂物体质量每增加,弹簧长度增加,据此得到函数关系式即可.
【详解】(1)解:由表格知,当时,,当时,,
答:当所挂重物为时,弹簧有,不挂重物时,弹簧有;
(2)解:∵所挂物体质量每增加,弹簧长度增加,
∴弹簧长度y与所挂物体质量x之间的函数关系式,
当时,,即当重物为时,弹簧有.
2.(2022下·福建漳州·七年级福建省诏安县第二实验中学校考期中)如图,是骆驼的体温随时间变化而变化的的关系图,据图回答下列问题:
(1)一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?
(2)从16时到24时,骆驼的体温下降了多少?
(3)在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?
(4)A点表示的是什么?
【答案】(1)35℃~40℃;12小时
(2)3℃
(3)4时到16时体温上升;0时到4时,16时到24时体温下降
(4)12时,骆驼的体温为39℃
【分析】观察0时到24时,骆驼的体温变化,进行解答即可.
【详解】(1)解:由图可知,最低体温为,最高体温为,
∴骆驼体温的变化范围为;
∵,
∴从最低体温上升到最高体温需要12小时.
(2)解:由图可知16时体温为,24时体温为
∵
∴骆驼体温下降了.
(3)解:由图可知,在4时到16时,骆驼体温上升;在0时到4时,16时到24时,骆驼体温下降.
(4)解:点表示,在12时,骆驼的体温为.
【点睛】本题考查了图象表示变量间的关系.解题的关键在于从图中获取正确的信息.
3.(2023上·河南焦作·八年级统考期中)新学期,两摞规格相同准备发放的课本整齐地叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(1)若(本)表示课本数,表示整齐叠放在桌面上的课本距离地面的高度,则是的一次函数,请求出关于的函数表达式;
(2)桌面上有55本与题(1)中相同的课本,整齐叠放成一摞,求这些数学课本距离地面的高度;
(3)小马说:如果把我班60名学生的这种课本整齐叠成一摞放在地面上,则它离地面有高.你认为小马的说法正确吗?请说明理由.
【答案】(1)
(2)这些课本距离地面的高度为
(3)小马的说法错误,理由见解析
【分析】本题主要考查了列代数式,求函数值:
(1)求出一本课本的高度,讲台高度,即可;
(2)将代入(1)中的解析式,求函数值即可;
(3)求出60本课本整齐叠成一摞放在地面上离地面的高度,即可求解.
【详解】(1)解:一本课本的高度,
讲台高度,
关于的函数表达式为:;
(2)解:当时,;
故这些课本距离地面的高度为;
(3)解:如果把这种课本整齐叠成一摞放在地面上,则它离地面的高度为,
,
小马的说法错误.
4.(2023下·陕西西安·七年级西安市第二十六中学校考阶段练习)如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分钟)的变化示意图,请根据图象回答下列问题:
(1)汽车匀速行驶了______分钟,时速是______千米/时;
(2)汽车在行驶途中在哪段时间停车休息?休息了多长时间?
(3)若司机从第28分钟开始先匀速行驶8分钟后,立即减速行驶2分钟,至停止.请你按照以上叙述在途中补画出从第28分钟以后汽车的速度与行驶时间的关系图.
【答案】(1)4,45
(2)汽车在行驶途中,在分钟这个时间段停车休息,休息了6分钟
(3)见解析
【分析】(1)直接由图象知汽车在段匀速行驶,进而可得结论;
(2)直接由图知,汽车在段的速度为0,进而可求解;
(3)根据题中描述补画图象即可.
【详解】(1)解:由图知,汽车匀速行驶了(分钟),时速是45千米/时,
故答案为:4,45;
(2)解:由图可知,汽车在段的速度为0,所以汽车在行驶途中,在分钟这个时间段停车休息,休息了(分钟).
(3)解:如图所示:
【点睛】本题考查用图象表示变量间的关系,理解题意,从图象上获取所需信息是解答的关键.
题型三 判别是否一次函数
例题:(2024上·甘肃兰州·八年级统考期末)下列各式①;②;③;④;⑤,是一次函数有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查了一次函数的定义,一般地,形如,(k为常数,)的函数叫做一次函数.根据定义分析即可.
【详解】解:①的右边不是整式,不是一次函数;
②的右边不是整式,不是一次函数;;
③是一次函数;
④的自变量的次数是2,不是一次函数;
⑤是一次函数.
故选B.
变式训练
1.(2023上·江苏淮安·八年级淮安市浦东实验中学校考阶段练习)函数(1) (2) (3) (4) (5) 中一次函数有 ( )
A.4个 B.3个 C.2个 D.1个
【答案】B
【分析】本题考查的是一次函数的定义,解决本题的关键是明确一次函数的定义,一般地,形如 (,k,b是常数)的函数,叫做一次函数.
利用一次函数的定义分析得出即可.
【详解】解:(1)是一次函数,符合题意;
(2)是一次函数,符合题意;
(3)中不是整式,不是一次函数,不符合题意;
(4)是一次函数,符合题意;
(5)的自变量的次数是2,不是一次函数,不符合题意;
故是一次函数的有3个.
故选:B.
2.(2023上·全国·八年级专题练习)函数①;②;③;④;⑤.是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【分析】本题考查了一次函数的定义,形如的函数,熟练掌握定义是解题的关键.
【详解】解:①,当时,不是一次函数;
②是一次函数;
③不是一次函数;
④是一次函数;
⑤不是一次函数;
所以是一次函数的有2个.
故选:B.
题型四 根据一次函数的定义求参数的值
例题:(2023上·浙江·八年级期末)若函数是一次函数,则m的值为_____.
【答案】1
【分析】本题考查了一次函数的定义,一般地,形如,(k为常数,)的函数叫做一次函数.由一次函数的定义可知且,从而可求得m的值.
【详解】解:∵是一次函数,
∴且,
解得且,
所以,
故答案为:1.
变式训练
1.(2024·全国·八年级假期作业)已知函数是关于的一次函数,则______,若该函数是正比例函数,则______,______.
【答案】 0
【分析】本题考查了正比例函数的定义:一般地,形如(k是常数,)的函数叫做正比例函数,其中k叫做比例系数.一次函数的定义:一般地,形如(,k、b是常数)的函数,叫做一次函数.根据一次函数的定义,正比例函数的定义求解即可.
【详解】解:当函数是关于x的一次函数时,,且,解得;
当函数是关于x的正比例函数时,,,且,解得,.
故答案为:,,0.
2.(2022上·四川成都·八年级成都嘉祥外国语学校校考期末)已知函数是关于x的一次函数,则_____.
【答案】
【分析】该题主要考查了一次函数的定义,解答的关键是熟悉一次函数的定义;
根据函数是一次函数,得出,进行解答即可;
【详解】解:根据题意得:,
解得:.
故答案为:.
题型五 画一次函数的图象
例题:(2023上·安徽滁州·八年级校考阶段练习)已知函数.
(1)请在所给的平面直角坐标系中画出该函数的图象.
(2)结合所画图象,分别求出在函数图象上满足下列条件的点的坐标:
①横坐标是;
②和轴的距离是2个单位长度.
【答案】(1)见解析
(2)①横坐标是的点是;②和轴的距离是2个单位长度的点的坐标为或
【分析】本题考查了画一次函数的图象,一次函数的性质,采用数形结合的思想是解此题的关键.
(1)根据解析式先求出函数与轴、轴的交点,即可画出图象;
(2)①将代入解析式进行计算求出的值即可;②由和轴的距离是2个单位长度得出或,分别代入计算,求出的值即可.
【详解】(1)解:在函数中,
当时,,则过,
当时,,解得:,则过,
画出该函数图象如图所示:
;
(2)解:①当时,,
横坐标是的点是;
②和轴的距离是2个单位长度,
或,
当时,,解得:,此时点的坐标为,
当时,,解得:,此时点的坐标为,
综上所述,和轴的距离是2个单位长度的点的坐标为或.
变式训练
1.(2023上·福建漳州·八年级福建省漳州第一中学校考阶段练习)已知,一次函数的图像分别与轴,轴交于点A,B.
(1)请直接写出两点坐标:A:__________,B:__________;
(2)在直角坐标系中画出函数图象(不用列表,直接描点、连线);
(3)点是一次函数上一动点,则的最小值为___________.
【答案】(1)
(2)见解析
(3)
【分析】本题考查了一次函数的图象,一次函数与坐标轴交点问题,勾股定理.
(1)根据题目即可求出A、B两点的坐标;
(2)根据(1)中A、B两点的坐标即可画出函数图象;
(3)先利用勾股定理求出,当与一次函数垂直时,有最小值,再根据等面积法,即可求出的最短距离.
【详解】(1)解:∵一次函数的图象分别与x轴、y轴交于点A、B,
∴当时,,
当时,,
∴A、B两点的坐标为,
故答案为:;
(2)解:由(1)得:A、B两点的坐标为,
∴函数图象如图所示:
(3)解:如图所示,当与一次函数垂直时,有最小值,
此时,,
,
,
,
,
故答案为:.
2.(2023上·宁夏银川·八年级银川唐徕回民中学校考期中)已知函数回答下列问题:
(1)画出函数的图象;当_________时,.
(2)设直线与轴交于点,与轴交于点,求出的面积.
(3)直线上是否存在一点(与不重合),使的面积等于8?若存在,求出点的坐标;若不存在,请说明理由.
【答案】(1)图象见解析,
(2)4
(3)存在,点C的坐标为或
【分析】本题考查了一次函数图象上点的坐标特征、一次函数的图象以及一次函数的性质,利用一次函数图象上点的坐标特征,求出点A,B的坐标并画出函数图象是解题的关键.
(1)利用一次函数图象上点的坐标特征,描点、连线,即可画出一次函数的图象,观察函数图象,即可得出当时,;
(2)由点A,B的坐标可得出,的长,再利用三角形的面积计算公式,即可求出的面积;
(3)设点的纵坐标为a,根据题意可得:,得出,再分别求出C点的坐标即可.
【详解】(1)解:当时,,
当时,,
解得:,
描点、连线,画出函数图象,如图所示.
由图象可知:当时,.
故答案为:;
(2)解:∵点A的坐标为,点B的坐标为,
∴,,
的面积为;
(3)存在点,使的面积等于8,理由如下:
设点的纵坐标为a,
根据题意可得:,
解得:,
当时,,解得:,
当时,,解得:,
所以点C的坐标为:或.
题型六 一次函数的图象和性质
例题:(2023上·广东深圳·八年级校考期中)下列关于函数的结论中,错误的是( )
A.图象经过点
B.点,在该函数图象上,若,则
C.将函数图象向下平移2个单位长度后,经过点
D.图象不经过第四象限
【答案】C
【分析】本题考查的是一次函数的性质,一次函数图象的平移,根据一次函数图象上点的坐标特点可判断A,根据一次函数的增减性可判断B,根据一次函数图象的平移可判断C,根据一次函数系数与经过的象限的关系可判断D,熟记一次函数的性质是解本题的关键.
【详解】解:A、当时,,故图象经过点,故本选项正确,不合题意;
B、函数中,,
随的增大而增大,
∵,
,故本选项正确,不合题意;
C、根据平移的规律,函数的图象向下平移2个单位长度得解析式为,所以当时,,则图象经过点,故本选项错误,符合题意;
D、,,,函数经过第一,二,三象限,不经过第四象限,故本选项正确,不符合题意.
故选:C.
变式训练
1.(2023下·广西南宁·八年级校考阶段练习)对于一次函数,下列说法正确的是( )
A.图象不经过第三象限
B.当时,
C.图象由直线向上平移2个单位长度得到
D.图象与x轴交于点
【答案】C
【分析】根据一次函数的图象与性质即可解答.
【详解】解:∵一次函数解析式为,
∴图象经过第一、二、三象限,故A不符合题意;
当时,,故B不符合题意;
直线向上平移2个单位得到的新解析式为,故C符合题意;
对于,令,则,
∴图象与x轴交于点,故D不符合题意.
故选C.
【点睛】本题考查一次函数的图象与性质.熟练掌握一次函数的图象与性质是解题关键.
2.(2023上·安徽六安·八年级校考阶段练习)一次函数,下列结论错误的是( )
A.若两点A(),B()在该函数图象上,且,则
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到的图象
D.函数的图象与轴的交点坐标是
【答案】D
【分析】分别根据一次函数的性质及函数图象平移的法则进行解答即可.
【详解】A、因为一次函数中,因此函数值随x的增大而减小,故A选项正确;
B、因为一次函数中,,因此此函数的图象经过一、二、四象限,不经过第三象限,故B选项正确;
C、由“上加下减”的原则可知,函数的图象向下平移4个单位长度得的图象,故C选项正确;
D、令,则,因此函数的图象与x轴的交点坐标是,故D选项错误.
故选:D.
【点睛】本题考查的是一次函数的性质及一次函数的图象与几何变换,熟知一次函数的性质及函数图象平移的法则是解答此题的关键.
题型七 根据一次函数经过的象限求参数问题
例题:(2023上·山东青岛·八年级统考期中)一次函数的图象不经过第________象限.
【答案】四/4
【分析】本题考查一次函数解析式及其性质,根据一次函数的解析式和一次函数的性质,可以得到即可得出该函数的图象经过哪几个象限,不经过哪个象限.
【详解】解:∵一次函数,,
∴一次函数经过一、二、三象限,不经过第四象限,
故答案为:四.
变式训练
1.(2023上·内蒙古包头·八年级校考期中)一次函数的图象不经过第三象限,则m的取值范围是____.
【答案】/
【分析】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线所在的位置与k、b的符号有直接的关系. 时,直线必经过一、三象限.时,直线必经过二、四象限.时,直线与y轴正半轴相交.时,直线过原点;时,直线与y轴负半轴相交.
【详解】解:∵一次函数的图象不经过第三象限,
∴,
解得:,
故答案为:.
2.(2024上·陕西西安·八年级西安市第二十六中学校联考期末)已知直线经过第二、四象限,则直线不经过第______象限.
【答案】三
【分析】本题考查正比例函数的性质和一次函数的性质,先利用正比例函数的性质得到,然后根据一次函数的性质求解即可.熟练掌握相关函数的性质是解题的关键.
【详解】解:∵直线经过第二、四象限,
∴,
∴,
又∵,
∴直线经过第一、二、四象限,
即直线不经过第三象限.
故答案为:三.
题型八 根据一次函数的增减性求参数问题
例题:(2024上·陕西西安·八年级统考期末)在一次函数中,随的增大而减小,则m的值可以是______.(写出一个即可)
【答案】(答案不唯一)
【分析】本题考查一次函数的性质,根据随的增大而减小,则,据此写出的值即可,答案不唯一.解题的关键是掌握:一次函数中,若,则随的增大而增大;若,则随的增大而减小,反过来也成立.
【详解】解:∵在一次函数中,随的增大而减小,
∴,
不妨设,
∴的值可以是.
故答案为:.
变式训练
1.(2023上·江苏徐州·八年级校考阶段练习)一次函数中,若y随x的增大而增大,则m的取值范围是___.
【答案】/
【分析】本题考查了一次函数图象与系数的关系.在一次函数中,函数值y随x的增大而减小;函数值y随x的增大而增大.当时,直线中y的值随x的增大而增大.通过解不等式来求m的取值范围.
【详解】解:∵直线中y的值随x的增大而减小,
,
解得,.
故答案为:.
2.(2024上·江苏·八年级泰州市姜堰区第四中学校考周测)若一次函数 的函数值随x的增大而增大,且函数的图像不经过第二象限,则k的取值范围是 _________
【答案】
【分析】本题考查了一次函数的性质,熟练掌握当k大于零时,函数值随x的增大而增大;图像与y轴的交点不高于原点,列式计算即可.
【详解】∵一次函数 的函数值随x的增大而增大,且函数的图像不经过第二象限,
∴,
解得,
故答案为:.
题型九 一次函数的图象与坐标轴的交点问题
例题:(2023上·陕西咸阳·八年级校考阶段练习)函数的图象与轴的交点是________.
【答案】
【分析】本题考查了一次函数的图像及性质,熟记“一次函数与轴有交点时函数值y为0”
【详解】解:当与轴有交点时,,
有,
解得:.
故答案为:.
变式训练
1.(2023上·海南海口·九年级海南中学校考阶段练习)一次函数与轴交点的坐标为________,与轴交点的坐标为________.
【答案】
【分析】根据一次函数解析式为,求出当时,的值,得出与轴交点的坐标;求出当时,的值,得出与轴交点的坐标即可.
【详解】解:∵一次函数解析式为,
∴当时,则,
解得:,
当时,则,
∴一次函数与轴交点的坐标为,与轴交点的坐标为.
故答案为:;.
【点睛】本题考查了一次函数图象与坐标轴的交点问题,明白坐标轴上点的坐标特点是解题的关键.
2.(2023上·福建福州·八年级福建省福州格致中学校考期中)直线与x轴的交点坐标是_____;与y轴的交点坐标是_____;与坐标轴围成的三角形面积为_____.
【答案】
【分析】分别令,,求出直线与x轴的交点坐标是;与y轴的交点坐标是,即可求解.
【详解】解:令,,
令,,
解得:,
∴直线与x轴的交点坐标是;与y轴的交点坐标是,
∴与坐标轴围成的三角形面积为.
故答案为:;;
【点睛】本题考查的是一次函数图象上点的坐标特点,熟知一次函数函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.另外要记住一次函数图象与坐标轴所围成的三角形的面积计算公式.
题型十 用待定系数法求一次函数的表达式
例题:(2023上·江苏扬州·八年级扬州教育学院附中校考阶段练习)已知一次函数.当时,;当时.
(1)求该一次函数的表达式;
(2)当时,求x的值.
【答案】(1)
(2)
【分析】本题考查了待定系数法求一次函数解析式,已知函数值求自变量的取值等知识.
(1)利用待定系数法即可求解;
(2)把代入一次函数解析式得到,解方程即可求解.
【详解】(1)解:∵一次函数,当时,;当时,
∴,
∴,
∴一次函数的表达式为;
(2)解:当时,,
解得.
变式训练
1.(2024上·安徽合肥·八年级统考期末)已知一次函数的图象与直线平行,且与轴交于点,求该一次函数的表达式.
【答案】
【分析】本题考查了平面直角坐标系内两条平行直线的函数解析式的性质,平面直角坐标系内直线与轴的交点问题,熟知两直线平行则k相等是解题的关键.根据直线与直线平行得到k的值;再根据直线交轴于点得到b的值,进而得出函数的表达式.
【详解】解:一次函数的图象与直线平行,
,
将点代入中,可得
,
一次函数的表达式为:.
2.(2024上·陕西榆林·八年级校考期末)如图,一次函数的图象与轴,轴分别交于点,且经过点.
(1)求一次函数的表达式.
(2)求的长.
【答案】(1)
(2)10
【分析】本题考查了待定系数法求一次函数解析式,勾股定理;
(1)待定系数法求解析式即可求解;
(2)先求得点的坐标为,然后根据勾股定理,即可求解.
【详解】(1)解:由题意可得,解得.
一次函数的表达式为.
(2)令,则,
解得,
点的坐标为,
.
令,则,
点的坐标为,
.
.
3.(2024上·安徽合肥·八年级统考期末)已知与成正比例,当时,.
(1)求y与x之间的关系式;
(2)求(1)中的函数图象与坐标轴围成的三角形的面积.
【答案】(1)
(2)
【分析】本题考查待定系数法求一次函数解析式,一次函数与坐标轴交点问题;
(1)设,当时,,求出,即可求出与之间的函数表达式;
(2)求出直线与、轴交点的坐标,即可得到,的长,根据三角形的面积公式,即可求解.
【详解】(1)解:与成正比例
设,
当时,,
,
,
,
即
与之间的函数表达式是,
(2)设直线与、轴分别交于、两点,
当时,,当时,,
的坐标是,的坐标是,
,,
函数图象与坐标轴围成的三角形面积是.
题型十一 一次函数与三角形的面积问题
例题:(2023春·河南郑州·八年级郑州外国语中学校考期末)如图,已知函数的图象与轴交于点,一次函数的图象经过点,与轴以及的图象分别交于点、,且点的横坐标为1.
(1)点的坐标是______直线的解析式是_______
(2)连接,求的面积.
(3)点是直线上一点(不与点重合),设点的横坐标为,的面积为,请直接写出与之间的关系式.
【答案】(1);
(2)
(3)
【分析】(1)根据D点横坐标及得出纵坐标进而得出D点坐标;最后通过两点坐标得出一次函数解析式;
(2)根据各点坐标即三角形面积公式即可求出;
(3)分情况讨论,利用图形面积的和差以及三角形的面积公式列式求解即可;
【详解】(1)将代入函数得D点纵坐标为2,将点,代入得:,解得,
故解析式为:
故答案为: ;;
(2)
如图:点A的坐标为,,点C的坐标为,
∴
;
(3)①如图,点P在之间:
;
②点P在B点下方,如图:
;
③点P在D点的上面
;
综上所述:
【点睛】本题考查待定系数法求一次函数解析式,一次函数与坐标轴围成的图形的面积的求解,会分割图形面积是关键.
变式训练
1.(2023秋·陕西西安·八年级校考期末)已知一次函数与的图像都过点,且与y轴分别交于点B,C.
(1)求m,n的值;
(2)求的面积.
【答案】(1),;
(2)4
【分析】(1)直接把点代入解析式,即可求出答案;
(2)分别求出B,C两点的坐标,然后利用面积公式,即可求出答案.
【详解】(1)解:∵一次函数与的图像都过点,
∴把点分别代入,得
,,
∴,;
(2)解:由(1)可知,,,
∴,,
分别令,则
,,
∴点B的坐标为,点C的坐标为;
∴,
∴的面积为:;
【点睛】本题考查了一次函数的图像和性质,一次函数与坐标轴的交点坐标,解题的关键是熟练掌握一次函数的性质进行解题.
2.(2023·江苏·八年级泰州市姜堰区第四中学校考期末)已知,一次函数的图像与x轴、y轴分别相交于A、B两点,点P的坐标为.
(1)若一次函数的图像经过点P,求m的值;
(2)若点P在x轴上,求的面积.
【答案】(1)0
(2)9
【分析】(1)将点P坐标代入一次函数表达式中,即可求出m值;
(2)首先根据一次函数表达式求出点A和点B坐标,再根据点P在x轴,可得纵坐标为0,可求出m值,从而得到点P坐标,结合坐标可得的面积.
【详解】(1)解:将点P代入中,
得,
解得:;
(2)在中,令,则,令,则,
∴,,
∵点P在x轴上,
∴,
∴,即,
∴.
【点睛】本题考查了一次函数图像上的点,一次函数与坐标轴的交点问题,解题的关键是求出相应点的坐标.
3.(2022秋·山东东营·七年级统考期末)已知某一次函数的图象经过点,且与正比例函数的图象相交于点,求:
(1)的值;
(2)一次函数y与x的函数解析式;
(3)这两个函数图象与轴所围成的三角形的面积.
【答案】(1)
(2)
(3)
【分析】(1)把交点坐标代入正比例函数解析式中求出a的值;
(2)将两点的坐标代入中,利用待定系数法求出一次函数解析式;
(3)先求得与x轴的交点A的坐标,再根据三角形面积公式进行计算.
【详解】(1)解:∵点在正比例函数的图象上,
∴;
(2)解:设一次函数的解析式为,
∵经过点,点,
∴,
解得,
∴一次函数的解析式为;
(3)解:∵时,,
∴,
∴与x轴的交点A为,
∵,
∴.
【点睛】本题主要是考查了待定系数法求解一次函数表达式以及求解与坐标轴的面积,正确利用待定系数法求出一次函数表达式,合理确定坐标轴围成的三角形的底和高,这是解决本题的关键.
第 页 共 页
