鲁教五四学制:2024-2025年九年级第一学期上册数学2.4解直角三角形 (3)学案
文档属性
| 名称 | 鲁教五四学制:2024-2025年九年级第一学期上册数学2.4解直角三角形 (3)学案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 16:59:17 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024--2025学年度九年级数学上册学案
2.4 解直角三角形(3)
【学习目标】
通过添加辅助线(作三角形一边的高),把解非直角三角形问题转化为解直角三角形问题.
【知识梳理】
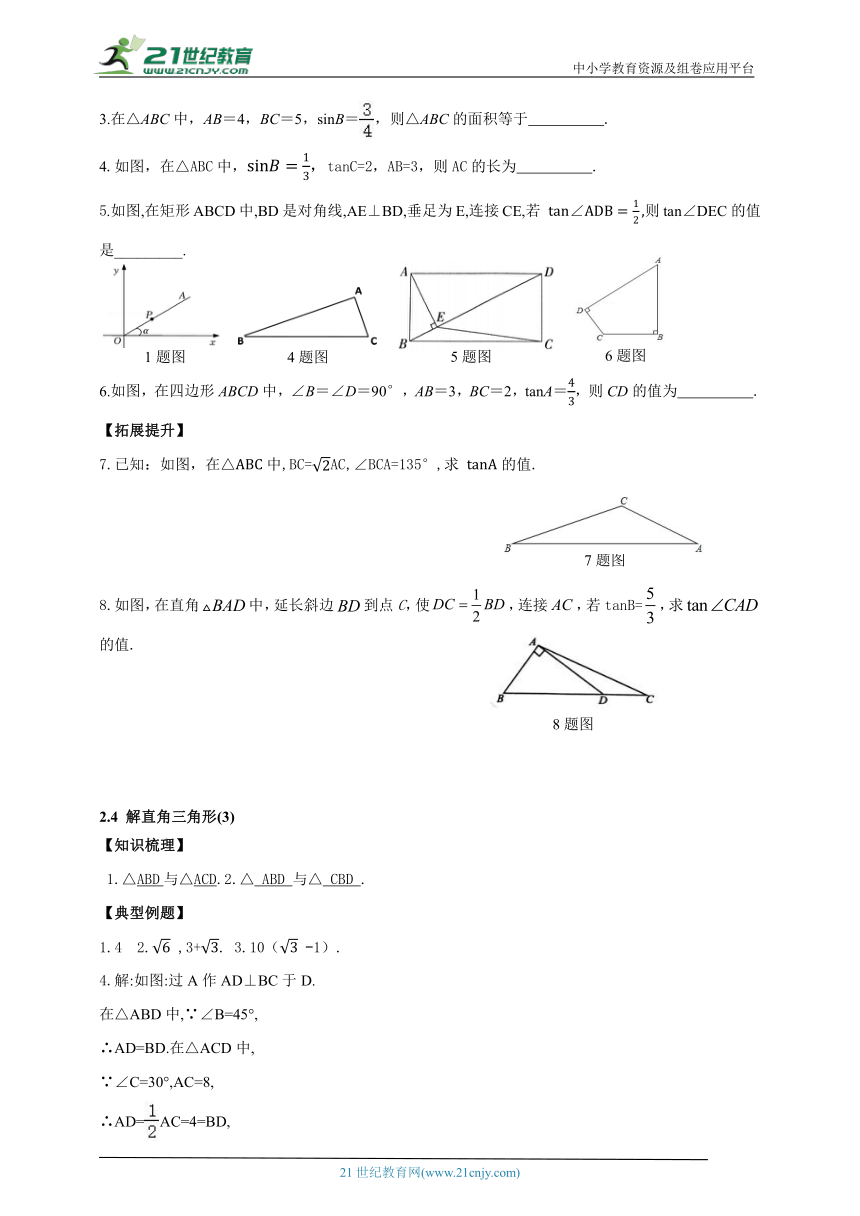
1.如图①所示在锐角△ABC中,过点A作AD⊥BC于点D,则△ 与△ 为直角三形.
2.如图②所示,在钝角△ABC中,过点B作BD⊥AC交AC延长线于点D,则△ 与
△ 为直角三形.
【典型例题】
知识点一 在锐角三角形中构造直角三角形
1.如图,△ABC中,∠ABC=60°,∠ACB=45°,AC=2,则AB=____________.
知识点二 在钝角三角形中构造直角三角形
2.如图所示,已知∠C=300,∠A=1050 ,AC=2,则AB= ,BC = .
3.如图所示,如图,在△ABC中,∠B=30°,∠C=135°,AC=10,则BC= .
4.如图,某中学有一块三角形状的花圃ABC,现可直接测量到∠B=45°,∠C=30°,AC=8米.请你求出BC的长.(结果可保留根号)
【巩固训练】
1.如图,在平面直角坐标系中,一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,若cosα=,则点P的坐标可能是( )
A.(3,5) B.(5,3) C.(3,4) D.(4,3)
2.在△ABC中,∠BAC=120°,AB=3,AC=2,则BC的长是 .
3.在△ABC中,AB=4,BC=5,sinB=,则△ABC的面积等于 .
4.如图,在△ABC中,,tanC=2,AB=3,则AC的长为 .
5.如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 则tan∠DEC的值是_________.
6.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为 .
【拓展提升】
7.已知:如图,在△中,BC=AC,∠BCA=135°,求 的值.
8.如图,在直角中,延长斜边到点C,使,连接,若tanB=,求的值.
2.4 解直角三角形(3)
【知识梳理】
1.△ABD与△ACD.2.△ ABD 与△ CBD .
【典型例题】
1.4 2. ,3+. 3.10( -1).
4.解:如图:过A作AD⊥BC于D.
在△ABD中,∵∠B=45°,
∴AD=BD.在△ACD中,
∵∠C=30°,AC=8,
∴AD=AC=4=BD,
∴CD==4,
∴BC=BD+CD=4+4,
答:BC的长为:(4+4)m.
【巩固训练】
1.D; 2.;3.;
4.; 5. 6.
7.解:过B点作BD⊥AC交AC的延长线于D点,则∠BCD=45°.
设AC=k,则有BD=CD=k,AD=2k,tanA=BD:AD=1:2 = 0.5.
8.解:如图,作CE⊥AD,
∴∠CED=90°
又∵∠BAD=90°,∠ADB=∠CDE
∴△CDE∽△BDA,
∵DC=BD
∴===,
∵tan B=,
∴设AD=5x,则AB=3x,
∴CE=x,DE=x,
∴tan∠CAD==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年度九年级数学上册学案
2.4 解直角三角形(3)
【学习目标】
通过添加辅助线(作三角形一边的高),把解非直角三角形问题转化为解直角三角形问题.
【知识梳理】
1.如图①所示在锐角△ABC中,过点A作AD⊥BC于点D,则△ 与△ 为直角三形.
2.如图②所示,在钝角△ABC中,过点B作BD⊥AC交AC延长线于点D,则△ 与
△ 为直角三形.
【典型例题】
知识点一 在锐角三角形中构造直角三角形
1.如图,△ABC中,∠ABC=60°,∠ACB=45°,AC=2,则AB=____________.
知识点二 在钝角三角形中构造直角三角形
2.如图所示,已知∠C=300,∠A=1050 ,AC=2,则AB= ,BC = .
3.如图所示,如图,在△ABC中,∠B=30°,∠C=135°,AC=10,则BC= .
4.如图,某中学有一块三角形状的花圃ABC,现可直接测量到∠B=45°,∠C=30°,AC=8米.请你求出BC的长.(结果可保留根号)
【巩固训练】
1.如图,在平面直角坐标系中,一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,若cosα=,则点P的坐标可能是( )
A.(3,5) B.(5,3) C.(3,4) D.(4,3)
2.在△ABC中,∠BAC=120°,AB=3,AC=2,则BC的长是 .
3.在△ABC中,AB=4,BC=5,sinB=,则△ABC的面积等于 .
4.如图,在△ABC中,,tanC=2,AB=3,则AC的长为 .
5.如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 则tan∠DEC的值是_________.
6.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为 .
【拓展提升】
7.已知:如图,在△中,BC=AC,∠BCA=135°,求 的值.
8.如图,在直角中,延长斜边到点C,使,连接,若tanB=,求的值.
2.4 解直角三角形(3)
【知识梳理】
1.△ABD与△ACD.2.△ ABD 与△ CBD .
【典型例题】
1.4 2. ,3+. 3.10( -1).
4.解:如图:过A作AD⊥BC于D.
在△ABD中,∵∠B=45°,
∴AD=BD.在△ACD中,
∵∠C=30°,AC=8,
∴AD=AC=4=BD,
∴CD==4,
∴BC=BD+CD=4+4,
答:BC的长为:(4+4)m.
【巩固训练】
1.D; 2.;3.;
4.; 5. 6.
7.解:过B点作BD⊥AC交AC的延长线于D点,则∠BCD=45°.
设AC=k,则有BD=CD=k,AD=2k,tanA=BD:AD=1:2 = 0.5.
8.解:如图,作CE⊥AD,
∴∠CED=90°
又∵∠BAD=90°,∠ADB=∠CDE
∴△CDE∽△BDA,
∵DC=BD
∴===,
∵tan B=,
∴设AD=5x,则AB=3x,
∴CE=x,DE=x,
∴tan∠CAD==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
