鲁教五四学制:2024-2025年九年级第一学期上册数学2.5三角函数的应用(2)学案
文档属性
| 名称 | 鲁教五四学制:2024-2025年九年级第一学期上册数学2.5三角函数的应用(2)学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024--2025学年度九年级数学上册学案
2.5 三角函数的应用(2)
【学习目标】
能熟练地应用解直角三角形解有关方位角、坡角(坡度)问题.
【知识梳理】
1.方向角通常以 为主,分南偏东(西)和北偏东(西),如北偏东300方向、南偏西450方向,且各个观测点 是互相平行的.
2.特殊的方向角,如东南方向、东北方向、西南方向、西北方向,夹角都为450
3.解决坡度问题时,可适当添加辅助线,将梯形分解为直角三角形和矩形来解决.
4.坡面的 和 的比叫做坡度.记作:i=; 与 的夹角叫做坡角 ,记为:α.即:i==tanα,坡度等于锐角α的 .
【典型例题】
知识点一 用解直角三角形解方向角问题
1.如图1,一艘轮船从位于灯塔的北偏东方向,距离灯塔60海里的小岛出发,沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,这时轮船与小岛的距离是( )
A.海里 B.海里 C.海里 D.海里
知识点二 用解直角三角形解坡角(坡度)问题
2.如图2所示,某拦水坝的横截面为梯形, 迎水坡的坡角为,且, 背水坡的坡度为是指坡面的铅直高度与水平宽度的比,坝面宽,坝高则坝底宽__________.
【巩固训练】
1.如图3,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为_____km.
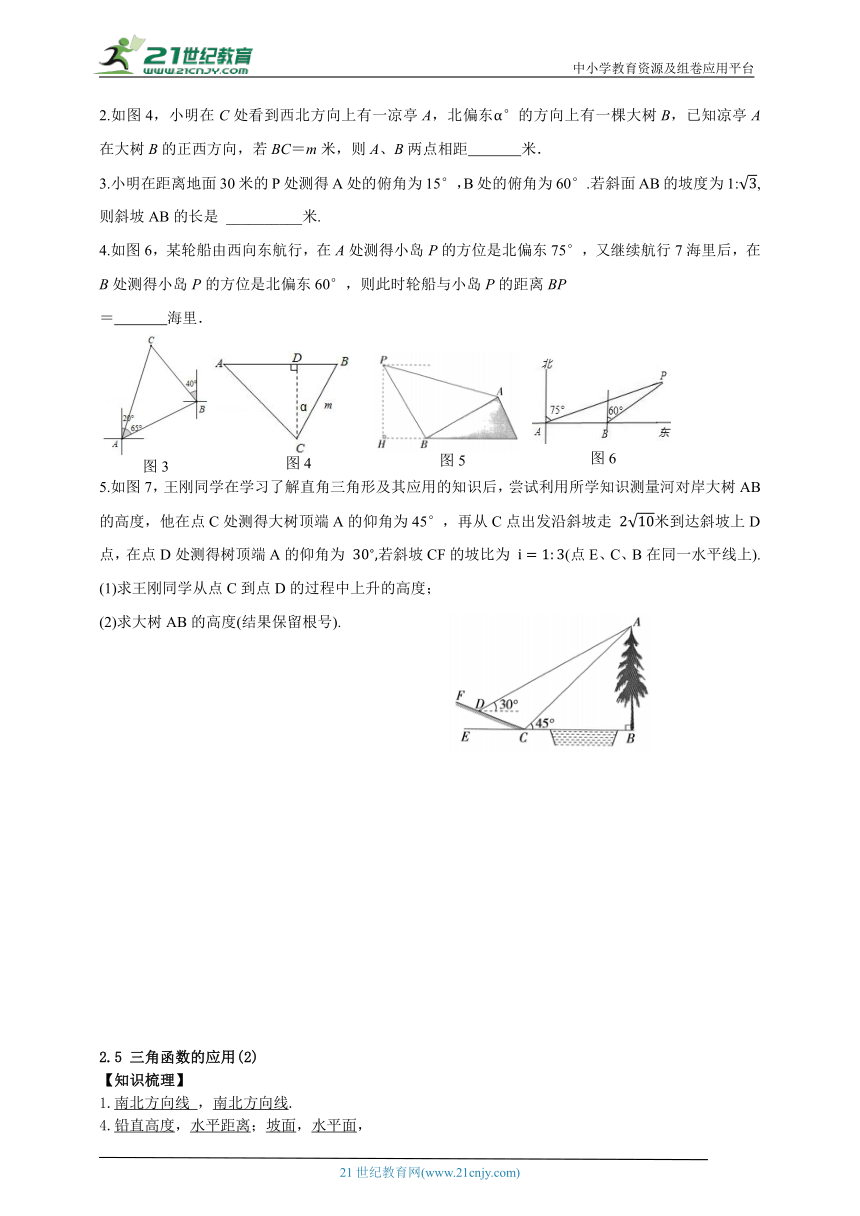
2.如图4,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距 米.
3.小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面AB的坡度为1:,则斜坡AB的长是 __________米.
4.如图6,某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP
= 海里.
5.如图7,王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走 米到达斜坡上D点,在点D处测得树顶端A的仰角为 若斜坡CF的坡比为 (点E、C、B在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).
2.5 三角函数的应用(2)
【知识梳理】
1.南北方向线 ,南北方向线.
4.铅直高度,水平距离;坡面,水平面,
正切值 .
【典型例题】
1. D.2. 49米 .
【巩固训练】
1.(30+10);2. m(cosα+sinα);
3. 20; 4. 7;
5. 解: (1)如图,过点D作DH⊥CE于点H.
∵斜坡CF的坡比为
设DH=x米,x>0,则CH=3x米,由勾股定理,得
即 ∴DH=2米.
答:王刚同学从点C到点D的过程中上升的高度为2米
(2)如图,过点D作DG⊥AB于点G,设BC=a米.
∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形.∴DH=BG=2米,DG=BH=(a+6)米.
米.∴AG=(a-2)米.
∵∠ADG=30°,∴tan∠ADC=tan30°,即 .
米.
答:大树AB的高度是()米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年度九年级数学上册学案
2.5 三角函数的应用(2)
【学习目标】
能熟练地应用解直角三角形解有关方位角、坡角(坡度)问题.
【知识梳理】
1.方向角通常以 为主,分南偏东(西)和北偏东(西),如北偏东300方向、南偏西450方向,且各个观测点 是互相平行的.
2.特殊的方向角,如东南方向、东北方向、西南方向、西北方向,夹角都为450
3.解决坡度问题时,可适当添加辅助线,将梯形分解为直角三角形和矩形来解决.
4.坡面的 和 的比叫做坡度.记作:i=; 与 的夹角叫做坡角 ,记为:α.即:i==tanα,坡度等于锐角α的 .
【典型例题】
知识点一 用解直角三角形解方向角问题
1.如图1,一艘轮船从位于灯塔的北偏东方向,距离灯塔60海里的小岛出发,沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,这时轮船与小岛的距离是( )
A.海里 B.海里 C.海里 D.海里
知识点二 用解直角三角形解坡角(坡度)问题
2.如图2所示,某拦水坝的横截面为梯形, 迎水坡的坡角为,且, 背水坡的坡度为是指坡面的铅直高度与水平宽度的比,坝面宽,坝高则坝底宽__________.
【巩固训练】
1.如图3,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为_____km.
2.如图4,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距 米.
3.小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面AB的坡度为1:,则斜坡AB的长是 __________米.
4.如图6,某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP
= 海里.
5.如图7,王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走 米到达斜坡上D点,在点D处测得树顶端A的仰角为 若斜坡CF的坡比为 (点E、C、B在同一水平线上).
(1)求王刚同学从点C到点D的过程中上升的高度;
(2)求大树AB的高度(结果保留根号).
2.5 三角函数的应用(2)
【知识梳理】
1.南北方向线 ,南北方向线.
4.铅直高度,水平距离;坡面,水平面,
正切值 .
【典型例题】
1. D.2. 49米 .
【巩固训练】
1.(30+10);2. m(cosα+sinα);
3. 20; 4. 7;
5. 解: (1)如图,过点D作DH⊥CE于点H.
∵斜坡CF的坡比为
设DH=x米,x>0,则CH=3x米,由勾股定理,得
即 ∴DH=2米.
答:王刚同学从点C到点D的过程中上升的高度为2米
(2)如图,过点D作DG⊥AB于点G,设BC=a米.
∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形.∴DH=BG=2米,DG=BH=(a+6)米.
米.∴AG=(a-2)米.
∵∠ADG=30°,∴tan∠ADC=tan30°,即 .
米.
答:大树AB的高度是()米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
