1.2 动量定理 (共23张PPT) 课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册
文档属性
| 名称 | 1.2 动量定理 (共23张PPT) 课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 14:16:19 | ||
图片预览








文档简介
(共23张PPT)
第一章 动量和动量守恒定律
第2节 动量定理
船靠岸时边缘上的废旧轮胎
摩托车头盔里的衬垫
跳高用的海绵垫
物体碰撞会受到力的作用,物体动量变化和力有什么关系?
01 动量定理的推导
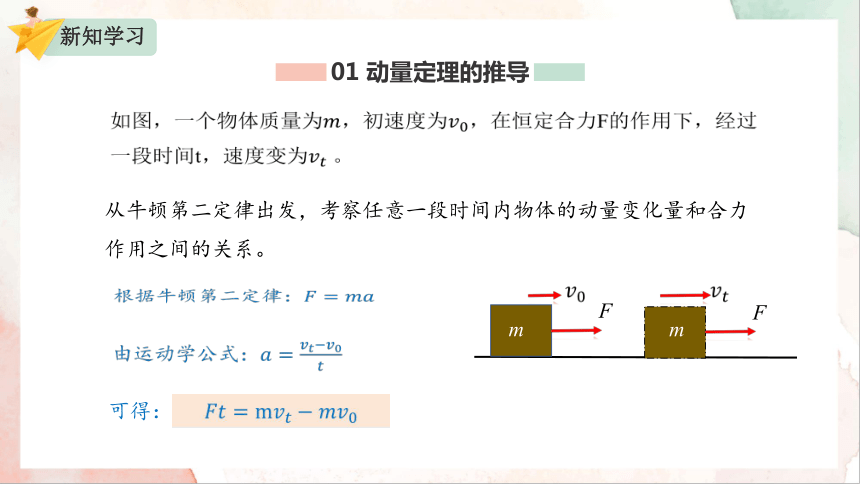
根据牛顿第二定律:
由运动学公式:
可得:
如图,一个物体质量为,初速度为,在恒定合力F的作用下,经过一段时间t,速度变为。
从牛顿第二定律出发,考察任意一段时间内物体的动量变化量和合力作用之间的关系。
F
F
m
m
1. 内容:物体在一个过程中所受力的冲量等于它始末的动量变化量。
2. 表达式:
(1)“力的冲量”是指合力的冲量
(2)表明合外力的冲量是动量变化的原因;
(3)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同。
3. 理解:
4.注意事项:动量定理可以适用于恒力,也可以用于变力。若是变力,动量定理中的力F通常取力在作用时间内的平均值。
(1)动量定理不但适用于恒力,也适用于随时间变化的变力,对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
(2)动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
(3)动量定理不仅适用于宏观低速物体,也适用于微观现象和高速运动问题。
动量定理的优点:不考虑中间过程,只考虑初末状态。
5. 动量定理的适用范围
(1)牛顿第二定律反映了力与加速度之间的瞬时对应关系,而动量定理反映了力作用一段时间的过程中,合力的冲量与物体初、末状态的动量变化间的关系;
6.动量定理与牛顿第二定律的区别
(2)牛顿第二定律只适用于宏观物体的低速运动,对高速运动的微观粒子不适用;而动量定理具有普适性。
02 动量定理的应用
应用1:解释生活现象
玻璃杯掉在坚硬的地面上很容易摔碎,掉在地毯上就不容易摔碎。
篮球运动员接球时,两手顺势后引,收缩至胸前
一定,延长作用时间,减小作用力。
应用2:快抽不倒,为什么
快抽时,摩擦力作用时间短,根据动量定理, 很小,末动量接近零。
例题:一辆质量为2200kg的汽车正在以90km/h的速度匀速行驶,突然前方出现复杂路段,如果驾驶员轻踩刹车制动,汽车在21s内停下;如果驾驶员急踩刹车制动,可在3.8s内使车停下。求这两种情况下使汽车停下的平均作用力。
应用3:汽车刹车时间短,冲击力大
变式:若例题中时间换成下表中的刹车时间,请根据不同的刹车时间分别计算要多大的平均作用力才能使汽车停下来,并计算从开始刹车到停下来所滑行到距离。
汽车刹车时间t/s 20 10 5 2.5 1
使汽车停下的 平均作用力F/N
汽车刹车过程 滑行的距离s/m
根据动量定理得: ;
-2750
-5500
-11000
-22000
-55000
根据动能定理得: 得: ,
代入每一次对应的平均力,求刹车过程滑行的距离,结果如下表:
汽车刹车时间 20 10 5 2.5 1
使汽车停下的 平均作用力 -2750 -5500 -11000 -22000 -55000
汽车刹车过程 滑行的距离 250 125 62.5 31.25 12.5
从表格中可以看出:
1.行驶中的汽车要想在紧急刹车时受到较小冲击力,必须有较长的刹车时间。
2.行车时要预判哪些情况下可能需要紧急刹车。如在三岔路口和靠近人群的地方,应提前减速,以减小紧急刹车时的冲击力和刹车过程滑行的距离,保证行车安全。
汽车安装安全气囊
乘车时佩戴安全带
思考:安全气囊、安全带为什么可以起到保护作用?
在剧烈碰撞时,安全带、安全气囊可以延长作用时间。依据动量定理可知一定时,增大作用时间,减小作用力,起到保护
例题:(1)如图所示,用质量为0.2kg的锤子水平敲击竖直墙壁上的一颗钉子。锤子接触钉子瞬间,速度的大小为5m/s,锤头反弹起来时,速度的大小为2m/s,锤子与钉子接触时间为0.1s,则锤子对钉子平均打击力?
v1
F
v2
解:取水平向右为正方向,
则:
设钉子对锤子的平均打击力大小为F:
由动量定理得:
解得:
由牛顿第三定律可知:
铁锤对钉子的平均打击力F,=F=14N,方向水平向右。
(2)改用一个质量为0.4kg的锤子捶打,若锤子捶打和反弹的速度不变,接触时间也不变,则锤子对钉子平均打击力大小是多少?
v1
F
v2
解:取水平向右为正方向,
则:
设钉子对锤子的平均打击力大小为F1:
由动量定理得:
解得:
由牛顿第三定律可知:
铁锤对钉子的平均打击力
(3)若锤子捶打速度的大小变为10m/s,反弹的速度大小不变,接触时间也不变,锤子质量为0.2kg,则锤子对钉子平均打击力大小是多少?
v1
F
v2
解:取水平向右为正方向,
则:
设钉子对锤子的平均打击力大小为F2:
由动量定理得:
解得:
由牛顿第三定律可知:
铁锤对钉子的平均打击力
思考:为什么我们通常用铁锤钉钉子?
缩短作用时间,增大作用力。
应用4:认识高空抛物的危险性
假设从20层高楼的楼顶(每层楼高约3米)落下一个质量0.1kg的苹果,苹果落地时与地面相撞,撞击时间为0.1s,请计算苹果落地时对地面的撞击力有多大。
解:以向下方向为正,
苹果做自由落体运动,
落地前瞬间速度为v:
解得:
解得:
根据动量定理:
鸡蛋从某一高度下落,分别与水泥地面和厚垫子接触前后的速度是相同的,因而在相互作用过程中鸡蛋的动量变化量相同。而两种情况下的相互作用时间不同,与水泥地面碰时作用时间短,与厚垫子相碰时作用时间较长,由 Ft =Δp 知,△p一定,t短则F大,t长则F小。所以鸡蛋落在水泥地面上会被摔碎而落到厚垫子上完好无损。
1.为什么鸡蛋落在水泥地面上会被摔碎而落到厚垫子上完好无损呢?
2.图片所示内容为汽车碰撞试验,一款轿车以p=20000 kg·m/s的动量撞击试验台,经t=0.1 s的时间停止运动。
(1)求撞击过程中的汽车受到的平均力大小。
(2)若汽车质量是1000 kg,求撞击前瞬间汽车的速度大小。
解析 (1)由动量定理得Ft=Δp,
代入数据解得F=2×105 N。
(2)由动量表达式知p=mv,代入数据得v=20 m/s。
3.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间 为0.002s。球棒对垒球的平均作用力是多大?
解:沿垒球飞向球棒时的方向建立坐标轴,垒球的初动量为
垒球的末动量为
由动量定理知垒球所受的平均作用力为
垒球所受的平均作用力的大小为6300 N,负号表示力的方向与坐标轴的方向相反,即力的方向与垒球飞来的方向相反。
p = mv = 0.18×25 kg·m/s = 4.5 kg·m/s
p' = mv' = (-0.18)×45 kg·m/s = - 8.1 kg·m/s
第一章 动量和动量守恒定律
第2节 动量定理
船靠岸时边缘上的废旧轮胎
摩托车头盔里的衬垫
跳高用的海绵垫
物体碰撞会受到力的作用,物体动量变化和力有什么关系?
01 动量定理的推导
根据牛顿第二定律:
由运动学公式:
可得:
如图,一个物体质量为,初速度为,在恒定合力F的作用下,经过一段时间t,速度变为。
从牛顿第二定律出发,考察任意一段时间内物体的动量变化量和合力作用之间的关系。
F
F
m
m
1. 内容:物体在一个过程中所受力的冲量等于它始末的动量变化量。
2. 表达式:
(1)“力的冲量”是指合力的冲量
(2)表明合外力的冲量是动量变化的原因;
(3)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同。
3. 理解:
4.注意事项:动量定理可以适用于恒力,也可以用于变力。若是变力,动量定理中的力F通常取力在作用时间内的平均值。
(1)动量定理不但适用于恒力,也适用于随时间变化的变力,对于变力,动量定理中的F应理解为变力在作用时间内的平均值;
(2)动量定理不仅可以解决匀变速直线运动的问题,还可以解决曲线运动中的有关问题,将较难的计算问题转化为较易的计算问题;
(3)动量定理不仅适用于宏观低速物体,也适用于微观现象和高速运动问题。
动量定理的优点:不考虑中间过程,只考虑初末状态。
5. 动量定理的适用范围
(1)牛顿第二定律反映了力与加速度之间的瞬时对应关系,而动量定理反映了力作用一段时间的过程中,合力的冲量与物体初、末状态的动量变化间的关系;
6.动量定理与牛顿第二定律的区别
(2)牛顿第二定律只适用于宏观物体的低速运动,对高速运动的微观粒子不适用;而动量定理具有普适性。
02 动量定理的应用
应用1:解释生活现象
玻璃杯掉在坚硬的地面上很容易摔碎,掉在地毯上就不容易摔碎。
篮球运动员接球时,两手顺势后引,收缩至胸前
一定,延长作用时间,减小作用力。
应用2:快抽不倒,为什么
快抽时,摩擦力作用时间短,根据动量定理, 很小,末动量接近零。
例题:一辆质量为2200kg的汽车正在以90km/h的速度匀速行驶,突然前方出现复杂路段,如果驾驶员轻踩刹车制动,汽车在21s内停下;如果驾驶员急踩刹车制动,可在3.8s内使车停下。求这两种情况下使汽车停下的平均作用力。
应用3:汽车刹车时间短,冲击力大
变式:若例题中时间换成下表中的刹车时间,请根据不同的刹车时间分别计算要多大的平均作用力才能使汽车停下来,并计算从开始刹车到停下来所滑行到距离。
汽车刹车时间t/s 20 10 5 2.5 1
使汽车停下的 平均作用力F/N
汽车刹车过程 滑行的距离s/m
根据动量定理得: ;
-2750
-5500
-11000
-22000
-55000
根据动能定理得: 得: ,
代入每一次对应的平均力,求刹车过程滑行的距离,结果如下表:
汽车刹车时间 20 10 5 2.5 1
使汽车停下的 平均作用力 -2750 -5500 -11000 -22000 -55000
汽车刹车过程 滑行的距离 250 125 62.5 31.25 12.5
从表格中可以看出:
1.行驶中的汽车要想在紧急刹车时受到较小冲击力,必须有较长的刹车时间。
2.行车时要预判哪些情况下可能需要紧急刹车。如在三岔路口和靠近人群的地方,应提前减速,以减小紧急刹车时的冲击力和刹车过程滑行的距离,保证行车安全。
汽车安装安全气囊
乘车时佩戴安全带
思考:安全气囊、安全带为什么可以起到保护作用?
在剧烈碰撞时,安全带、安全气囊可以延长作用时间。依据动量定理可知一定时,增大作用时间,减小作用力,起到保护
例题:(1)如图所示,用质量为0.2kg的锤子水平敲击竖直墙壁上的一颗钉子。锤子接触钉子瞬间,速度的大小为5m/s,锤头反弹起来时,速度的大小为2m/s,锤子与钉子接触时间为0.1s,则锤子对钉子平均打击力?
v1
F
v2
解:取水平向右为正方向,
则:
设钉子对锤子的平均打击力大小为F:
由动量定理得:
解得:
由牛顿第三定律可知:
铁锤对钉子的平均打击力F,=F=14N,方向水平向右。
(2)改用一个质量为0.4kg的锤子捶打,若锤子捶打和反弹的速度不变,接触时间也不变,则锤子对钉子平均打击力大小是多少?
v1
F
v2
解:取水平向右为正方向,
则:
设钉子对锤子的平均打击力大小为F1:
由动量定理得:
解得:
由牛顿第三定律可知:
铁锤对钉子的平均打击力
(3)若锤子捶打速度的大小变为10m/s,反弹的速度大小不变,接触时间也不变,锤子质量为0.2kg,则锤子对钉子平均打击力大小是多少?
v1
F
v2
解:取水平向右为正方向,
则:
设钉子对锤子的平均打击力大小为F2:
由动量定理得:
解得:
由牛顿第三定律可知:
铁锤对钉子的平均打击力
思考:为什么我们通常用铁锤钉钉子?
缩短作用时间,增大作用力。
应用4:认识高空抛物的危险性
假设从20层高楼的楼顶(每层楼高约3米)落下一个质量0.1kg的苹果,苹果落地时与地面相撞,撞击时间为0.1s,请计算苹果落地时对地面的撞击力有多大。
解:以向下方向为正,
苹果做自由落体运动,
落地前瞬间速度为v:
解得:
解得:
根据动量定理:
鸡蛋从某一高度下落,分别与水泥地面和厚垫子接触前后的速度是相同的,因而在相互作用过程中鸡蛋的动量变化量相同。而两种情况下的相互作用时间不同,与水泥地面碰时作用时间短,与厚垫子相碰时作用时间较长,由 Ft =Δp 知,△p一定,t短则F大,t长则F小。所以鸡蛋落在水泥地面上会被摔碎而落到厚垫子上完好无损。
1.为什么鸡蛋落在水泥地面上会被摔碎而落到厚垫子上完好无损呢?
2.图片所示内容为汽车碰撞试验,一款轿车以p=20000 kg·m/s的动量撞击试验台,经t=0.1 s的时间停止运动。
(1)求撞击过程中的汽车受到的平均力大小。
(2)若汽车质量是1000 kg,求撞击前瞬间汽车的速度大小。
解析 (1)由动量定理得Ft=Δp,
代入数据解得F=2×105 N。
(2)由动量表达式知p=mv,代入数据得v=20 m/s。
3.一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间 为0.002s。球棒对垒球的平均作用力是多大?
解:沿垒球飞向球棒时的方向建立坐标轴,垒球的初动量为
垒球的末动量为
由动量定理知垒球所受的平均作用力为
垒球所受的平均作用力的大小为6300 N,负号表示力的方向与坐标轴的方向相反,即力的方向与垒球飞来的方向相反。
p = mv = 0.18×25 kg·m/s = 4.5 kg·m/s
p' = mv' = (-0.18)×45 kg·m/s = - 8.1 kg·m/s
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
