1.5 弹性碰撞与非弹性碰撞 (共21张PPT) 课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册
文档属性
| 名称 | 1.5 弹性碰撞与非弹性碰撞 (共21张PPT) 课件 2024-2025学年高二物理粤教版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 14:20:05 | ||
图片预览








文档简介
(共21张PPT)
第一章 动量和动量守恒定律
第5节 弹性碰撞与非弹性碰撞
碰撞是自然界中常见的现象,你能列举出一些碰撞现象吗?
汽车之间的碰撞
网球和球拍的碰撞
肢体之间的碰撞
思考:那么如果从能量的角度去研究碰撞前后物体动能的变化,该如何对碰撞进行分类呢?
物体碰撞时,通常作用时间很短,相互作用的内力很大,因此,外力往往可以忽略不计,满足动量守恒条件。下面我们从能量的角度研究碰撞前后物体动能的变化情况,进而对碰撞进行分类。
知识点一:碰撞
1.概念:两个或两个以上的物体在相遇的极短时间内产生非常大的相互作用。
2.特点:
(1)作用时间极短;
(2)系统所受外力远小于内力,可认为系统的总动量守恒;
(3)可忽略物体的位移,认为物体在碰撞前后仍在同一位置;
(4)碰撞前的总动能总是大于或等于碰撞后的总动能。
【观察与思考】用如图所示的实验装置做如下实验:
(1)两个相同的刚性球悬挂于同一水平面,两悬点的距离等于刚性球的直径大小,线长相等,将其中一球拉开至一定角度,松手后使之与另一球发生正碰。
(2)在两个球分别套上尼龙搭扣做的套圈,做同样的碰撞。
记下碰撞后两球达到的最大高度,并思考下列问题。
(1)在以上两种情况下,两个球碰撞前后的总机械能是否相等?可能的原因是什么?
(2)如果碰撞前后总机械能不相等,是否违反了机械能守恒定律?
(3)总结以上两种碰撞情况的区别。
【观察与思考】用如图所示的实验装置做如下实验:
(1)两个相同的刚性球悬挂于同一水平面,两悬点的距离等于刚性球的直径大小,线长相等,将其中一球拉开至一定角度,松手后使之与另一球发生正碰。
(2)在两个球分别套上尼龙搭扣做的套圈,做同样的碰撞。
结论:
在(1)情况下,两球碰撞前后的总机械能相等;
在(2)情况下,两球碰撞前后的总机械能不相等,但并不违反能量守恒定律。
(1)定义:如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
(2)特点:碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
即:EK1=EK2
3. 弹性碰撞
弹性形变
钢球、玻璃球碰撞时,机械能损失很小,它们的碰撞可以看作弹性碰撞。
(1)定义:如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
(2)特点:碰撞后不能完全恢复形变,碰撞过程中系统机械能减少。
即:EK1>EK2
4. 非弹性碰撞
非弹性形变
橡皮泥球碰撞时,它们的碰撞是非弹性碰撞。
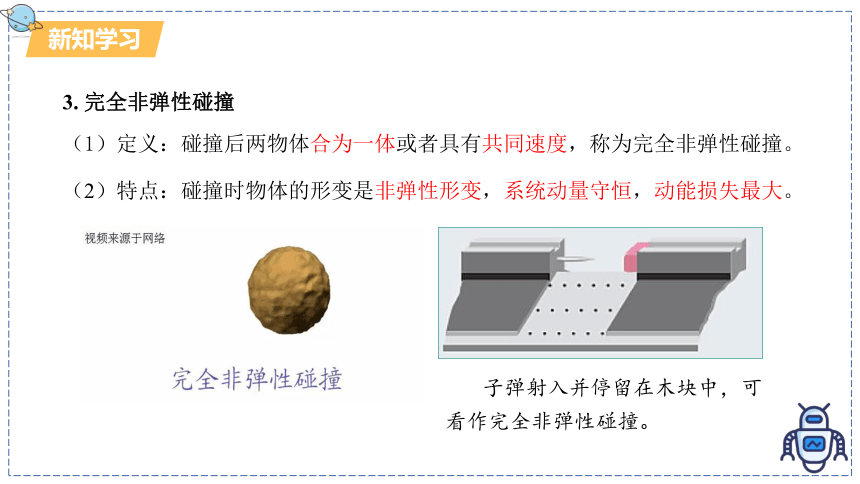
3. 完全非弹性碰撞
(1)定义:碰撞后两物体合为一体或者具有共同速度,称为完全非弹性碰撞。
(2)特点:碰撞时物体的形变是非弹性形变,系统动量守恒,动能损失最大。
子弹射入并停留在木块中,可看作完全非弹性碰撞。
知识点二:直线上的弹性碰撞和非弹性碰撞的规律分析
如图所示,质量为m2的物体B静止在光滑水平面上,物体B的左端连有轻弹簧,质量为m1的物体A以速度v1向B运动.在Ⅰ位置,物体A与物体B的轻弹簧刚好接触,弹簧开始被压缩,物体A开始减速,物体B开始加速;到Ⅱ位置,物体A,B的速度刚好相等(设为v),弹簧被压缩到最短;到Ⅲ位置,物体A,B的速度分别为v1′和v2′ .分以下三种情况讨论全过程系统动量和能量变化情况.
(1)在Ⅲ位置,弹簧可以恢复到原长.
(2)在Ⅲ位置,弹簧只能部分恢复,不能回到原长.
(3)在Ⅱ位置,弹簧弹性失效.
(1)在Ⅲ位置,弹簧可以恢复到原长,弹簧发生弹性形变。
【解析】
Ⅰ→Ⅱ,系统减少的动能全部转化为弹性势能;
在Ⅱ位置,系统动能最小而弹性势能最大;
Ⅱ→Ⅲ,系统减少的弹性势能全部转化为动能;
因此在Ⅰ、Ⅲ位置,系统动能相等.这种碰撞是弹性碰撞.
由动量守恒定律和机械能守恒定律,有
①
②
联立①②解得物体A,B的最终速度分别为
③
④
(2)在Ⅲ位置,弹簧只能部分恢复,不能回到原长,弹簧发生塑性形变。
Ⅰ→Ⅱ,系统减少的动能部分转化为弹性势能,部分转化为内能;
在Ⅱ位置,系统动能仍和(1)相同,弹性势能仍最大,但比(1)小;
Ⅱ→Ⅲ,系统减少的弹性势能部分转化为动能,部分转化为内能;
因此全过程系统的动能有损失(部分动能转化为内能).
这种碰撞是非弹性碰撞.
(3)在Ⅱ位置,两物体速度相等时弹簧完全失效,不再恢复。
Ⅰ→Ⅱ,系统减少的动能全部转化为内能;
在Ⅱ位置,系统动能仍和(1)相同,但没有弹性势能;
由于没有弹性,物体A,B不再分开,而是以速度v ′共同运动;
由动量守恒定律,有
解得
这种碰撞是完全非弹性碰撞.系统动能损失最大,设为
解得
1 0,= 等质量物体弹性碰撞速度交换(如打台球)
2 大撞小,同向跑
3 ,= 碰后速度几乎没变,仍按原速度运动,
以的速度的两倍向前运动。
4 , 小撞大,被弹回
5 ,=0 碰后被按原来速率弹回,几乎末动。
在(1)弹性碰撞中
C
1. 在光滑水平面上相向运动的两小球发生正碰后一起沿原来的速度方向运动,这说明原来( )
A.球的质量一定大于球的质量
B.球的速度一定大于球的速度
C.球的动量一定大于球的动量
D.球的动能一定大于球的动能
2. 甲、乙两球在光滑水平轨道上运动,它们的动量分别是5和7,甲追上乙并发生碰撞,碰撞后乙球的动量变为10,则两球质量与的关系可能是( )
A.
B.
C.
D.
C
3.如图所示,用轻弹簧相连的质量均为2 kg的A、B两物块静止于光滑的水平地面上,弹簧处于原长;质量为4 kg的物块C以v=6 m/s的初速度在光滑水平地面上向右运动,与前方的物块A发生碰撞(碰撞时间极短),并且C与A碰撞后二者粘在一起运动。在以后的运动中:
(1)当弹簧的弹性势能最大时,物体B的速度多大 弹簧弹性势能的最大值是多大
(2)弹簧第一次恢复原长时,B的速度多大
(1)物体B的速度为4m/s,弹簧弹性势能的最大值是12J
(2)弹簧第一次恢复原长时,B的速度为6m/s
弹性碰撞和非弹性碰撞
按照能量变化分类
弹性碰撞
非弹性碰撞
完全非弹性碰撞
特例
直线上的弹性碰撞和非弹性碰撞的规律分析
第一章 动量和动量守恒定律
第5节 弹性碰撞与非弹性碰撞
碰撞是自然界中常见的现象,你能列举出一些碰撞现象吗?
汽车之间的碰撞
网球和球拍的碰撞
肢体之间的碰撞
思考:那么如果从能量的角度去研究碰撞前后物体动能的变化,该如何对碰撞进行分类呢?
物体碰撞时,通常作用时间很短,相互作用的内力很大,因此,外力往往可以忽略不计,满足动量守恒条件。下面我们从能量的角度研究碰撞前后物体动能的变化情况,进而对碰撞进行分类。
知识点一:碰撞
1.概念:两个或两个以上的物体在相遇的极短时间内产生非常大的相互作用。
2.特点:
(1)作用时间极短;
(2)系统所受外力远小于内力,可认为系统的总动量守恒;
(3)可忽略物体的位移,认为物体在碰撞前后仍在同一位置;
(4)碰撞前的总动能总是大于或等于碰撞后的总动能。
【观察与思考】用如图所示的实验装置做如下实验:
(1)两个相同的刚性球悬挂于同一水平面,两悬点的距离等于刚性球的直径大小,线长相等,将其中一球拉开至一定角度,松手后使之与另一球发生正碰。
(2)在两个球分别套上尼龙搭扣做的套圈,做同样的碰撞。
记下碰撞后两球达到的最大高度,并思考下列问题。
(1)在以上两种情况下,两个球碰撞前后的总机械能是否相等?可能的原因是什么?
(2)如果碰撞前后总机械能不相等,是否违反了机械能守恒定律?
(3)总结以上两种碰撞情况的区别。
【观察与思考】用如图所示的实验装置做如下实验:
(1)两个相同的刚性球悬挂于同一水平面,两悬点的距离等于刚性球的直径大小,线长相等,将其中一球拉开至一定角度,松手后使之与另一球发生正碰。
(2)在两个球分别套上尼龙搭扣做的套圈,做同样的碰撞。
结论:
在(1)情况下,两球碰撞前后的总机械能相等;
在(2)情况下,两球碰撞前后的总机械能不相等,但并不违反能量守恒定律。
(1)定义:如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
(2)特点:碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
即:EK1=EK2
3. 弹性碰撞
弹性形变
钢球、玻璃球碰撞时,机械能损失很小,它们的碰撞可以看作弹性碰撞。
(1)定义:如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
(2)特点:碰撞后不能完全恢复形变,碰撞过程中系统机械能减少。
即:EK1>EK2
4. 非弹性碰撞
非弹性形变
橡皮泥球碰撞时,它们的碰撞是非弹性碰撞。
3. 完全非弹性碰撞
(1)定义:碰撞后两物体合为一体或者具有共同速度,称为完全非弹性碰撞。
(2)特点:碰撞时物体的形变是非弹性形变,系统动量守恒,动能损失最大。
子弹射入并停留在木块中,可看作完全非弹性碰撞。
知识点二:直线上的弹性碰撞和非弹性碰撞的规律分析
如图所示,质量为m2的物体B静止在光滑水平面上,物体B的左端连有轻弹簧,质量为m1的物体A以速度v1向B运动.在Ⅰ位置,物体A与物体B的轻弹簧刚好接触,弹簧开始被压缩,物体A开始减速,物体B开始加速;到Ⅱ位置,物体A,B的速度刚好相等(设为v),弹簧被压缩到最短;到Ⅲ位置,物体A,B的速度分别为v1′和v2′ .分以下三种情况讨论全过程系统动量和能量变化情况.
(1)在Ⅲ位置,弹簧可以恢复到原长.
(2)在Ⅲ位置,弹簧只能部分恢复,不能回到原长.
(3)在Ⅱ位置,弹簧弹性失效.
(1)在Ⅲ位置,弹簧可以恢复到原长,弹簧发生弹性形变。
【解析】
Ⅰ→Ⅱ,系统减少的动能全部转化为弹性势能;
在Ⅱ位置,系统动能最小而弹性势能最大;
Ⅱ→Ⅲ,系统减少的弹性势能全部转化为动能;
因此在Ⅰ、Ⅲ位置,系统动能相等.这种碰撞是弹性碰撞.
由动量守恒定律和机械能守恒定律,有
①
②
联立①②解得物体A,B的最终速度分别为
③
④
(2)在Ⅲ位置,弹簧只能部分恢复,不能回到原长,弹簧发生塑性形变。
Ⅰ→Ⅱ,系统减少的动能部分转化为弹性势能,部分转化为内能;
在Ⅱ位置,系统动能仍和(1)相同,弹性势能仍最大,但比(1)小;
Ⅱ→Ⅲ,系统减少的弹性势能部分转化为动能,部分转化为内能;
因此全过程系统的动能有损失(部分动能转化为内能).
这种碰撞是非弹性碰撞.
(3)在Ⅱ位置,两物体速度相等时弹簧完全失效,不再恢复。
Ⅰ→Ⅱ,系统减少的动能全部转化为内能;
在Ⅱ位置,系统动能仍和(1)相同,但没有弹性势能;
由于没有弹性,物体A,B不再分开,而是以速度v ′共同运动;
由动量守恒定律,有
解得
这种碰撞是完全非弹性碰撞.系统动能损失最大,设为
解得
1 0,= 等质量物体弹性碰撞速度交换(如打台球)
2 大撞小,同向跑
3 ,= 碰后速度几乎没变,仍按原速度运动,
以的速度的两倍向前运动。
4 , 小撞大,被弹回
5 ,=0 碰后被按原来速率弹回,几乎末动。
在(1)弹性碰撞中
C
1. 在光滑水平面上相向运动的两小球发生正碰后一起沿原来的速度方向运动,这说明原来( )
A.球的质量一定大于球的质量
B.球的速度一定大于球的速度
C.球的动量一定大于球的动量
D.球的动能一定大于球的动能
2. 甲、乙两球在光滑水平轨道上运动,它们的动量分别是5和7,甲追上乙并发生碰撞,碰撞后乙球的动量变为10,则两球质量与的关系可能是( )
A.
B.
C.
D.
C
3.如图所示,用轻弹簧相连的质量均为2 kg的A、B两物块静止于光滑的水平地面上,弹簧处于原长;质量为4 kg的物块C以v=6 m/s的初速度在光滑水平地面上向右运动,与前方的物块A发生碰撞(碰撞时间极短),并且C与A碰撞后二者粘在一起运动。在以后的运动中:
(1)当弹簧的弹性势能最大时,物体B的速度多大 弹簧弹性势能的最大值是多大
(2)弹簧第一次恢复原长时,B的速度多大
(1)物体B的速度为4m/s,弹簧弹性势能的最大值是12J
(2)弹簧第一次恢复原长时,B的速度为6m/s
弹性碰撞和非弹性碰撞
按照能量变化分类
弹性碰撞
非弹性碰撞
完全非弹性碰撞
特例
直线上的弹性碰撞和非弹性碰撞的规律分析
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
