1.3 动量守恒定律 (共22张PPT) 课件 2024-2025学年高二物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 1.3 动量守恒定律 (共22张PPT) 课件 2024-2025学年高二物理人教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第一章 动量守恒定律
第3节 动量守恒定律
1.能运用动量定理分析碰撞现象中的动量变化。
2.在了解系统、内力和外力的基础上,理解动量守恒定律。
3.了解动量守恒定律的普遍适用性和牛顿运动定律适用范围的局限性。
对于冰壶等物体的碰撞也是这样么?怎样证明这一结论?这是一个普遍的规律么?
第一节中我们通过分析一辆小车碰撞一辆静止小车,得出碰撞前后两辆小车的动量之和不变的结论。
F
F·Δt= mv' – mv0=Δp
v0
接下来我们用动量定理分别研究两个相互作用的物体,看看是否会有新收获?
F
m1
m2
动量定理给出了单个物体受力与动量变化量之间的关系
01 相互作用的两个物体的动量改变
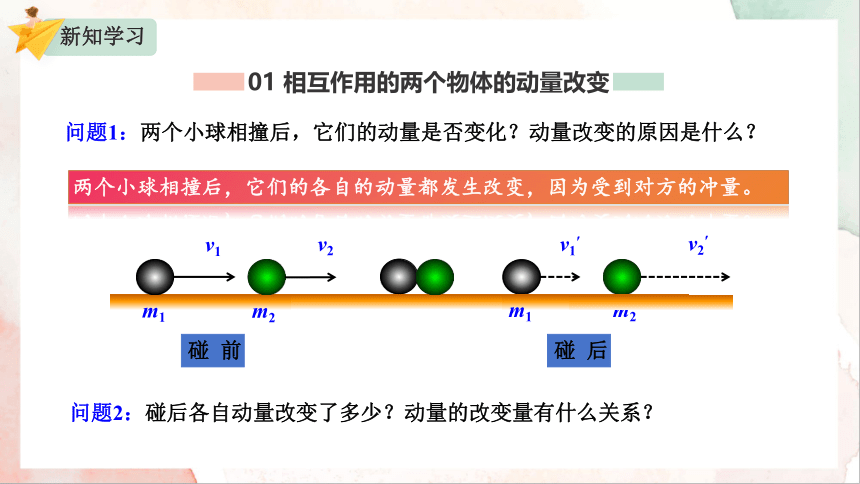
问题1:两个小球相撞后,它们的动量是否变化?动量改变的原因是什么?
两个小球相撞后,它们的各自的动量都发生改变,因为受到对方的冲量。
问题2:碰后各自动量改变了多少?动量的改变量有什么关系?
v1
v2
v1′
v2′
m1
m1
m2
m2
碰 前
碰 后
A
B
m2
m1
m2
m1
m2
m1
A
B
光滑
F2
F1
取向右为正方向
对A:
对B:
根据牛顿第三定律:
两个物体碰撞后的动量之和等于碰撞前的动量之和
v> v
p′1+ p′2= p1+ p2
v
A
B
m2
m1
m2
m1
N1
G1
N2
G2
F1
F2
系统
内力
外力
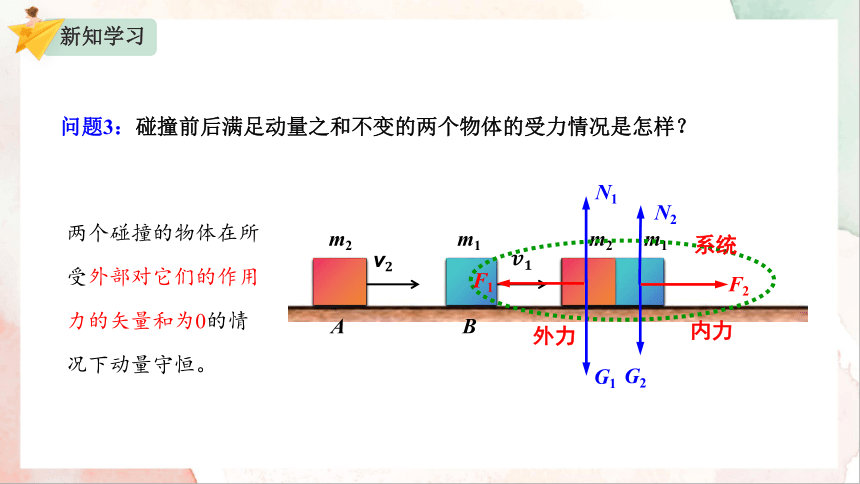
问题3:碰撞前后满足动量之和不变的两个物体的受力情况是怎样?
两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
系统:我们把两个(或多个)相互作用的物体构成的整体叫做系统。
内力:系统内物体间的相互作用力叫做内力。
外力:系统以外的物体施加给系统内物体的力,叫做外力。
m2
m1
N1
G1
N2
G2
F1
F2
系统
内力
外力
如果一个系统不受外力,或者所受合外力为0,无论这一系统的内部发生了何种形式的相互作用,这个系统的总动量保持不变。
1.内容:
2.公式:
(1)m1v1+m2v2=m1v1'+m2v2'
3.条件:
(1)系统不受外力;
(2)系统受到外力,但外力的合力为零。
(2)m1 v1= -m2 v2
02 动量守恒定律
(3)系统所受外力合力不为零,但系统内力远大于外力(如碰撞、爆炸等),外力相对来说可以忽略不计,因而系统动量近似守恒;(近似条件)
(4)系统总的来看虽不符合以上三条中的任何一条,但在某一方向上符合以上三条中的某一条,则系统在这一方向上动量守恒.(单向条件)
m
v1
v2
mv1+(-Mv2)=0
4.动量守恒定律的几个特性:
系统性 研究对象是相互作用的两个或多个物体组成的系统
相对性 应用时,系统中各物体在相互作用前后的速度必须相对于同一惯性系,通常均为对地的速度
瞬时性 初动量必须是系统中各物体在相互作用前同一时刻的动量,末动量必须是系统中各物体在相互作用后同一时刻的动量,不同时刻的动量一般不能相加
矢量性 对于作用前后物体的运动方向都在同一直线上的问题,应先选取正方向,与选取的正方向一致的动量为正值,相反的为负值
思考与讨论:如图所示,静止的两辆小车用细线相连,中间有一个压缩了的轻质弹簧。烧断细线后,由于弹力的作用,两辆小车分别向左、右运动,它们都获得了动量,它们的总动量是否增加了?
弹簧对两辆小车的作用力大小相等,方向相反,两辆小车受到的外力的矢量和为0,系统总动量守恒。
烧断细线后,两辆小车动量大小相等,方向相反,总动量仍为0。
烧断细线前,系统静止,总动量为0;
例题:如图,在列车编组站里,一辆质量为1.8×104 kg的货车在平直轨道上以v1=2 m/s 的速度运动,碰上一辆质量为2.2×104 kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
③本题中研究的是哪一个过程?该过程的初状态和末状态分别是什么?
①本题中相互作用的系统是什么?
②分析系统受到哪几个外力的作用?是否符合动量守恒的条件?
m1
m2
系统
N1
N2
F2
内力
外力
F1
G1
G2
分析:
解: 已知 m1=1.8×104 kg ,m2=2.2×104 kg 。沿碰撞前货车运动的方向建立坐标轴,有 v1=2 m/s 。设两车结合后的速度为 v 。
两车碰撞前的总动量为: p=m1v1
碰撞后的总动量为: p′=(m1+m2)v
根据动量守恒定律可得: (m1+m2)v=m1v1
解出 v== m/s=0.9 m/s
两车结合后速度的大小为 0.9 m/s;v是正值,表示两车结合后仍沿坐标轴方向运动,即仍然向右运动。
o
x
应用动量守恒定律解题的基本步骤
(1)找:找研究对象(系统包括那几个物体)和研究过程;
(2)析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
(3)定:规定正方向,确定初末状态动量正负号;
(4)列:由动量守恒定律列方程;
(5)解:解方程,得出最后的结果,并对结果进行分析。
(1)牛顿运动定律和动量守恒定律不是等价的,动量守恒定律是一个独立的实验定律,它适用于目前为止物理学研究的一切领域,而牛顿运动定律只适用于宏观、低速的情形。
思考:既然许多问题可以通过牛顿运动定律解决,为什么还要研究动量守恒定律?
03 动量守恒定律的普适性
(2)应用动量守恒定律解决碰撞等问题时不涉及过程中的复杂受力情况,只涉及过程始末两个状态,与过程中力的细节无关。这样,问题往往能大大简化。
(3)动量守恒定律适用于任何形式的相互作用过程——碰撞、黏合、断裂、爆炸等。我们无法了解这些过程的细节,重要考察系统所受到合外力是否为零,以及系统中各部分的初末动量。这是应用动量守恒定律解题的优点。
1.(多选)关于动量守恒的条件,下列说法正确的是 ( )
A.只要系统内有摩擦力,动量就不可能守恒
B.只要系统所受合外力为零,系统动量就守恒
C.系统加速度为零,系统动量一定守恒
D.只要系统所受合外力不为零,则系统在任何方向上动量都不可能守恒
BC
2.如图所示,两木块A、B用轻质弹簧连在一起,置于光滑的水平面上。一颗子弹水平射入木块A,并留在其中。在子弹打中木块A及弹簧被压缩的整个过程中,对子弹、两木块和弹簧组成的系统,下列说法中正确的是( )
A.动量守恒、机械能守恒
B.动量守恒、机械能不守恒
C.动量不守恒、机械能守恒
D.动量、机械能都不守恒
B
3.如图所示,质量为m的光滑弧形槽静止在光滑水平面上,槽底部与水平面平滑连接,一个质量也为m的小球从槽上高h处由静止开始下滑,则小球下滑过程中( )
A.小球和槽组成的系统动量守恒
B.槽对小球的支持力不做功
C.重力对小球做功的瞬时功率一直增大
D.地球、小球和槽组成的系统机械能守恒
D
4.质量M=2 kg的小平板车静止在光滑水平面上,车的一端静止着质量mA=2 kg的木块A(可视为质点),如图所示。一颗质量mB=20 g的子弹以600 m/s的水平速度射穿A后,速度变为100 m/s,最后木块A未从车上掉下,求平板车最后的速度。
答案 2.5 m/s
第一章 动量守恒定律
第3节 动量守恒定律
1.能运用动量定理分析碰撞现象中的动量变化。
2.在了解系统、内力和外力的基础上,理解动量守恒定律。
3.了解动量守恒定律的普遍适用性和牛顿运动定律适用范围的局限性。
对于冰壶等物体的碰撞也是这样么?怎样证明这一结论?这是一个普遍的规律么?
第一节中我们通过分析一辆小车碰撞一辆静止小车,得出碰撞前后两辆小车的动量之和不变的结论。
F
F·Δt= mv' – mv0=Δp
v0
接下来我们用动量定理分别研究两个相互作用的物体,看看是否会有新收获?
F
m1
m2
动量定理给出了单个物体受力与动量变化量之间的关系
01 相互作用的两个物体的动量改变
问题1:两个小球相撞后,它们的动量是否变化?动量改变的原因是什么?
两个小球相撞后,它们的各自的动量都发生改变,因为受到对方的冲量。
问题2:碰后各自动量改变了多少?动量的改变量有什么关系?
v1
v2
v1′
v2′
m1
m1
m2
m2
碰 前
碰 后
A
B
m2
m1
m2
m1
m2
m1
A
B
光滑
F2
F1
取向右为正方向
对A:
对B:
根据牛顿第三定律:
两个物体碰撞后的动量之和等于碰撞前的动量之和
v> v
p′1+ p′2= p1+ p2
v
A
B
m2
m1
m2
m1
N1
G1
N2
G2
F1
F2
系统
内力
外力
问题3:碰撞前后满足动量之和不变的两个物体的受力情况是怎样?
两个碰撞的物体在所受外部对它们的作用力的矢量和为0的情况下动量守恒。
系统:我们把两个(或多个)相互作用的物体构成的整体叫做系统。
内力:系统内物体间的相互作用力叫做内力。
外力:系统以外的物体施加给系统内物体的力,叫做外力。
m2
m1
N1
G1
N2
G2
F1
F2
系统
内力
外力
如果一个系统不受外力,或者所受合外力为0,无论这一系统的内部发生了何种形式的相互作用,这个系统的总动量保持不变。
1.内容:
2.公式:
(1)m1v1+m2v2=m1v1'+m2v2'
3.条件:
(1)系统不受外力;
(2)系统受到外力,但外力的合力为零。
(2)m1 v1= -m2 v2
02 动量守恒定律
(3)系统所受外力合力不为零,但系统内力远大于外力(如碰撞、爆炸等),外力相对来说可以忽略不计,因而系统动量近似守恒;(近似条件)
(4)系统总的来看虽不符合以上三条中的任何一条,但在某一方向上符合以上三条中的某一条,则系统在这一方向上动量守恒.(单向条件)
m
v1
v2
mv1+(-Mv2)=0
4.动量守恒定律的几个特性:
系统性 研究对象是相互作用的两个或多个物体组成的系统
相对性 应用时,系统中各物体在相互作用前后的速度必须相对于同一惯性系,通常均为对地的速度
瞬时性 初动量必须是系统中各物体在相互作用前同一时刻的动量,末动量必须是系统中各物体在相互作用后同一时刻的动量,不同时刻的动量一般不能相加
矢量性 对于作用前后物体的运动方向都在同一直线上的问题,应先选取正方向,与选取的正方向一致的动量为正值,相反的为负值
思考与讨论:如图所示,静止的两辆小车用细线相连,中间有一个压缩了的轻质弹簧。烧断细线后,由于弹力的作用,两辆小车分别向左、右运动,它们都获得了动量,它们的总动量是否增加了?
弹簧对两辆小车的作用力大小相等,方向相反,两辆小车受到的外力的矢量和为0,系统总动量守恒。
烧断细线后,两辆小车动量大小相等,方向相反,总动量仍为0。
烧断细线前,系统静止,总动量为0;
例题:如图,在列车编组站里,一辆质量为1.8×104 kg的货车在平直轨道上以v1=2 m/s 的速度运动,碰上一辆质量为2.2×104 kg的静止的货车,它们碰撞后结合在一起继续运动。求货车碰撞后运动的速度。
③本题中研究的是哪一个过程?该过程的初状态和末状态分别是什么?
①本题中相互作用的系统是什么?
②分析系统受到哪几个外力的作用?是否符合动量守恒的条件?
m1
m2
系统
N1
N2
F2
内力
外力
F1
G1
G2
分析:
解: 已知 m1=1.8×104 kg ,m2=2.2×104 kg 。沿碰撞前货车运动的方向建立坐标轴,有 v1=2 m/s 。设两车结合后的速度为 v 。
两车碰撞前的总动量为: p=m1v1
碰撞后的总动量为: p′=(m1+m2)v
根据动量守恒定律可得: (m1+m2)v=m1v1
解出 v== m/s=0.9 m/s
两车结合后速度的大小为 0.9 m/s;v是正值,表示两车结合后仍沿坐标轴方向运动,即仍然向右运动。
o
x
应用动量守恒定律解题的基本步骤
(1)找:找研究对象(系统包括那几个物体)和研究过程;
(2)析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
(3)定:规定正方向,确定初末状态动量正负号;
(4)列:由动量守恒定律列方程;
(5)解:解方程,得出最后的结果,并对结果进行分析。
(1)牛顿运动定律和动量守恒定律不是等价的,动量守恒定律是一个独立的实验定律,它适用于目前为止物理学研究的一切领域,而牛顿运动定律只适用于宏观、低速的情形。
思考:既然许多问题可以通过牛顿运动定律解决,为什么还要研究动量守恒定律?
03 动量守恒定律的普适性
(2)应用动量守恒定律解决碰撞等问题时不涉及过程中的复杂受力情况,只涉及过程始末两个状态,与过程中力的细节无关。这样,问题往往能大大简化。
(3)动量守恒定律适用于任何形式的相互作用过程——碰撞、黏合、断裂、爆炸等。我们无法了解这些过程的细节,重要考察系统所受到合外力是否为零,以及系统中各部分的初末动量。这是应用动量守恒定律解题的优点。
1.(多选)关于动量守恒的条件,下列说法正确的是 ( )
A.只要系统内有摩擦力,动量就不可能守恒
B.只要系统所受合外力为零,系统动量就守恒
C.系统加速度为零,系统动量一定守恒
D.只要系统所受合外力不为零,则系统在任何方向上动量都不可能守恒
BC
2.如图所示,两木块A、B用轻质弹簧连在一起,置于光滑的水平面上。一颗子弹水平射入木块A,并留在其中。在子弹打中木块A及弹簧被压缩的整个过程中,对子弹、两木块和弹簧组成的系统,下列说法中正确的是( )
A.动量守恒、机械能守恒
B.动量守恒、机械能不守恒
C.动量不守恒、机械能守恒
D.动量、机械能都不守恒
B
3.如图所示,质量为m的光滑弧形槽静止在光滑水平面上,槽底部与水平面平滑连接,一个质量也为m的小球从槽上高h处由静止开始下滑,则小球下滑过程中( )
A.小球和槽组成的系统动量守恒
B.槽对小球的支持力不做功
C.重力对小球做功的瞬时功率一直增大
D.地球、小球和槽组成的系统机械能守恒
D
4.质量M=2 kg的小平板车静止在光滑水平面上,车的一端静止着质量mA=2 kg的木块A(可视为质点),如图所示。一颗质量mB=20 g的子弹以600 m/s的水平速度射穿A后,速度变为100 m/s,最后木块A未从车上掉下,求平板车最后的速度。
答案 2.5 m/s
