2.4 单摆 (共25张PPT) 课件 2024-2025学年高二物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 2.4 单摆 (共25张PPT) 课件 2024-2025学年高二物理人教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第二章 机械振动
第4节 单摆
1.知道单摆的概念,了解单摆运动的特点;
2.知道单摆的受力特点以及实际摆看成单摆的条件;
3.知道单摆周期与摆长、重力加速度的定量关系,并能进行有关计算。
秋千的摆动
钟摆的摆动
游乐大摆锤的摆动
1.以上生活中的摆动有什么共同的特点?
2.结合你已经学习过的理想化模型和摆动物体的特点,你是否可以简化出一种新的理想化的物理模型呢?
1.定义:如果细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
2.单摆的结构:
(1)固定悬点O'
(2)摆长:悬点到重心的距离
L
(3)θ :最大摆角
θ
理想化模型
知识点一:单 摆
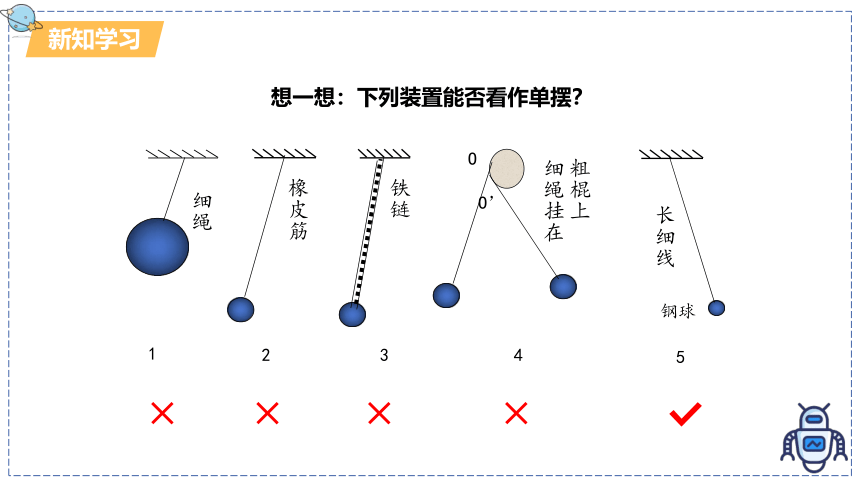
想一想:下列装置能否看作单摆?
铁链
粗棍上
细绳挂在
细绳
橡皮筋
2
3
4
1
O
O’
长细线
5
钢球
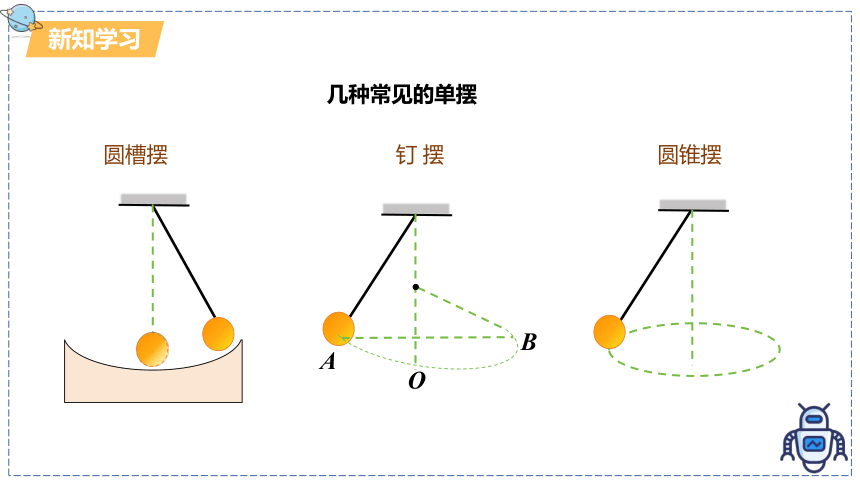
几种常见的单摆
圆槽摆
圆锥摆
钉 摆
A
B
O
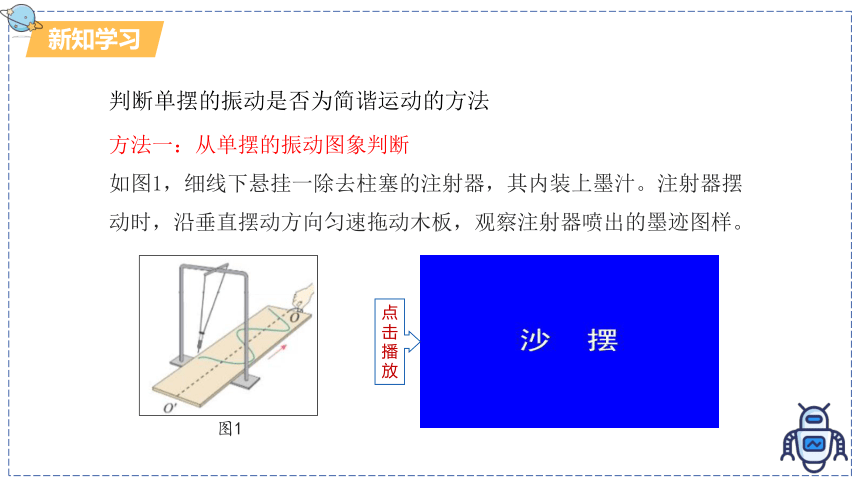
判断单摆的振动是否为简谐运动的方法
方法一:从单摆的振动图象判断
如图1,细线下悬挂一除去柱塞的注射器,其内装上墨汁。注射器摆动时,沿垂直摆动方向匀速拖动木板,观察注射器喷出的墨迹图样。
图1
点击播放
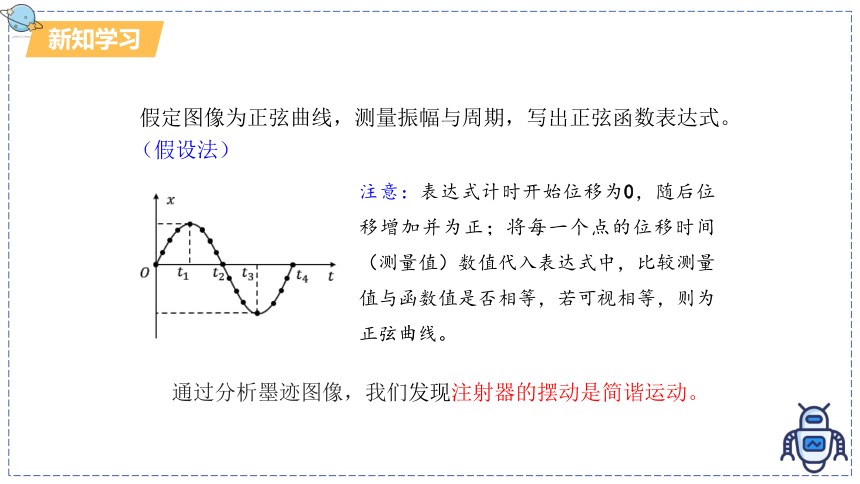
注意:表达式计时开始位移为0,随后位移增加并为正;将每一个点的位移时间(测量值)数值代入表达式中,比较测量值与函数值是否相等,若可视相等,则为正弦曲线。
通过分析墨迹图像,我们发现注射器的摆动是简谐运动。
(假设法)
假定图像为正弦曲线,测量振幅与周期,写出正弦函数表达式。
方法二:从单摆的受力特征判断
分析单摆受到的回复力是否满足
摆球的受力分析:
(1)任意位置
如图所示,G2=Gcos θ,F-G2的作用就是提供摆球绕O′做变速圆周运动的向心力; G1 =Gsin θ的作用是提供摆球以O为中心做往复运动的回复力。
(2)平衡位置
摆球经过平衡位置时,G2=G,G1=0,此时F应大于G,F-G提供向心力,因此,在平衡位置,回复力F回=0,与G1=0相符。
(3)单摆的简谐运动
在θ很小时(理论值为<5°),
G1方向与摆球位移方向相反,所以有回复力
因此,在摆角θ很小时,单摆做简谐运动。
① 弧长 ≈ x
(弧度值)
②
所以
(令)
知识点二:单摆的回复力
1.回复力的来源
摆球的重力沿圆弧切线方向的分力。
2.回复力的特点
在偏角很小时,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总指向平衡位置,即 。
注:回复力不是摆球所受的合外力。在平衡位置处,回复力为0,但小球受到的合力并不为0(指向悬点,提供小球做圆周运动的向心力)。
单摆的运动特点:
(1)摆线以悬点为圆心做变速圆周运动,因此在运动过程中只要速度v≠0,半径方向都受向心力。
(2)摆线同时以平衡位置为中心做往复运动,因此在运动过程中只要不在平衡位置,轨迹的切线方向都受回复力。
知识点三:单摆的周期
思考:一根短绳系一个小球,它的振动周期较短。悬绳较长的秋千,周期较长。单摆的周期与哪些因素有关?
1.探究单摆周期与摆长之间的关系
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定角度后同时释放,观察两摆的振动周期。
探究方法:控制变量法
研究单摆的振幅、质量、摆长对周期的影响。
实验一:将摆长相同、质量相同摆球拉到不同高度(即:振幅不同都在小偏角下)自由释放,观察两摆的摆动情况。
实验二:将摆长相同、质量不同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
实验三:将摆长不同、质量相同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
在同一个地方,单摆周期T与摆球质量和振幅无关,仅与摆长有关系,且摆长越长,周期越大。
2. 探究单摆周期与摆长之间的定量关系
改变摆长 l,测出对应的单摆周期 T(在小偏角下)。根据你的实验数据,尝试在坐标纸上画出 T-l 图像。看看是什么曲线?你能根据 T-l 图像判断单摆周期与摆长的关系吗?
周期T/s 1.48 1.55 1.79 2.19
摆长l/m 0.5 0.6 0.8 1.1
不能
再根据你的实验数据,在坐标纸上画出T-l2 图像。它是什么曲线?你能根据T-l2图像判断单摆周期与摆长的关系吗?
周期T/s 1.48 1.55 1.79 2.19
摆长l2 /m2 0.25 0.36 0.64 1.21
在误差允许的范围内单摆周期与摆长的平方成正比。
3. 单摆的周期公式
(2)国际单位:秒(s)
惠更斯
T = 2π
(1)周期公式:
荷兰物理学家惠更斯进行了详尽的研究,发现单摆做简谐运动的周期 T 与摆长 l 的二次方根成正比,与重力加速度 g 的二次方根成反比,而与振幅、摆球质量无关。
(3)单摆周期公式的应用和理解
周期公式的应用:由单摆周期公式可得g= ,只要测出单摆的摆长 l 和周期T就可算出当地的重力加速度。
由公式可知,某单摆做简谐运动(摆角小于5°)的周期只与其摆长 l 和当地的重力加速度 g 有关,而与振幅或摆球质量无关。摆长、重力加速度都一定时,周期和频率也一定,通常称为单摆的固有周期和固有频率。
实际的单摆摆球不可能是质点,所以摆长应是从悬点到摆球球心的长度,即 ,l1为摆线长,d为摆球直径。
思考:如果将单摆从赤道移到北京,周期会怎么变化?如果将单摆从海面移到高山,周期又会怎么变化?
如果将单摆从赤道移到北京,周期将变小
如果将单摆从海面移到高山,周期将变大
重力加速度g:由单摆所在的空间位置决定。
纬度越低,高度越高,g值就越小。
不同星球上g值也不同。
T =2
1.(多选)关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的拉力作用
B.摆球受重力、摆线的拉力、回复力作用
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的拉力大小比摆球的重力大
AC
2.图中O点为单摆的固定悬点,现将摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程( )
A.摆球在A点和C点处,速度为零,合力也为零
B.摆球在A点和C点处,速度为零,回复力也为零
C.摆球在B点处,速度最大,回复力也最大
D.摆球在B点处,速度最大,向心力也最大
D
3.一个单摆的摆长为,在其悬点O的正下方0.19处有一钉子P(如图所示),现将摆球向左拉开到A,使摆线偏角<5°,放手后使其摆动,摆动到B的过程中摆角也小于5°,求出单摆的振动周期。
解:释放后摆球到达右边最高点B处,由机械能守恒可知B和A等高,则摆球始终做简谐运动。
小球在左边的周期为T1=2π
小球在右边的周期为T2=2π
则整个单摆的周期为T=+=π+π=1.9π
单摆
单摆:
单摆的回复力:摆球重力沿切线方向的分力
单摆的周期:
理想化模型
第二章 机械振动
第4节 单摆
1.知道单摆的概念,了解单摆运动的特点;
2.知道单摆的受力特点以及实际摆看成单摆的条件;
3.知道单摆周期与摆长、重力加速度的定量关系,并能进行有关计算。
秋千的摆动
钟摆的摆动
游乐大摆锤的摆动
1.以上生活中的摆动有什么共同的特点?
2.结合你已经学习过的理想化模型和摆动物体的特点,你是否可以简化出一种新的理想化的物理模型呢?
1.定义:如果细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
2.单摆的结构:
(1)固定悬点O'
(2)摆长:悬点到重心的距离
L
(3)θ :最大摆角
θ
理想化模型
知识点一:单 摆
想一想:下列装置能否看作单摆?
铁链
粗棍上
细绳挂在
细绳
橡皮筋
2
3
4
1
O
O’
长细线
5
钢球
几种常见的单摆
圆槽摆
圆锥摆
钉 摆
A
B
O
判断单摆的振动是否为简谐运动的方法
方法一:从单摆的振动图象判断
如图1,细线下悬挂一除去柱塞的注射器,其内装上墨汁。注射器摆动时,沿垂直摆动方向匀速拖动木板,观察注射器喷出的墨迹图样。
图1
点击播放
注意:表达式计时开始位移为0,随后位移增加并为正;将每一个点的位移时间(测量值)数值代入表达式中,比较测量值与函数值是否相等,若可视相等,则为正弦曲线。
通过分析墨迹图像,我们发现注射器的摆动是简谐运动。
(假设法)
假定图像为正弦曲线,测量振幅与周期,写出正弦函数表达式。
方法二:从单摆的受力特征判断
分析单摆受到的回复力是否满足
摆球的受力分析:
(1)任意位置
如图所示,G2=Gcos θ,F-G2的作用就是提供摆球绕O′做变速圆周运动的向心力; G1 =Gsin θ的作用是提供摆球以O为中心做往复运动的回复力。
(2)平衡位置
摆球经过平衡位置时,G2=G,G1=0,此时F应大于G,F-G提供向心力,因此,在平衡位置,回复力F回=0,与G1=0相符。
(3)单摆的简谐运动
在θ很小时(理论值为<5°),
G1方向与摆球位移方向相反,所以有回复力
因此,在摆角θ很小时,单摆做简谐运动。
① 弧长 ≈ x
(弧度值)
②
所以
(令)
知识点二:单摆的回复力
1.回复力的来源
摆球的重力沿圆弧切线方向的分力。
2.回复力的特点
在偏角很小时,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总指向平衡位置,即 。
注:回复力不是摆球所受的合外力。在平衡位置处,回复力为0,但小球受到的合力并不为0(指向悬点,提供小球做圆周运动的向心力)。
单摆的运动特点:
(1)摆线以悬点为圆心做变速圆周运动,因此在运动过程中只要速度v≠0,半径方向都受向心力。
(2)摆线同时以平衡位置为中心做往复运动,因此在运动过程中只要不在平衡位置,轨迹的切线方向都受回复力。
知识点三:单摆的周期
思考:一根短绳系一个小球,它的振动周期较短。悬绳较长的秋千,周期较长。单摆的周期与哪些因素有关?
1.探究单摆周期与摆长之间的关系
在铁架台的横梁上固定两个单摆,按照以下几种情况,把它们拉起一定角度后同时释放,观察两摆的振动周期。
探究方法:控制变量法
研究单摆的振幅、质量、摆长对周期的影响。
实验一:将摆长相同、质量相同摆球拉到不同高度(即:振幅不同都在小偏角下)自由释放,观察两摆的摆动情况。
实验二:将摆长相同、质量不同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
实验三:将摆长不同、质量相同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
在同一个地方,单摆周期T与摆球质量和振幅无关,仅与摆长有关系,且摆长越长,周期越大。
2. 探究单摆周期与摆长之间的定量关系
改变摆长 l,测出对应的单摆周期 T(在小偏角下)。根据你的实验数据,尝试在坐标纸上画出 T-l 图像。看看是什么曲线?你能根据 T-l 图像判断单摆周期与摆长的关系吗?
周期T/s 1.48 1.55 1.79 2.19
摆长l/m 0.5 0.6 0.8 1.1
不能
再根据你的实验数据,在坐标纸上画出T-l2 图像。它是什么曲线?你能根据T-l2图像判断单摆周期与摆长的关系吗?
周期T/s 1.48 1.55 1.79 2.19
摆长l2 /m2 0.25 0.36 0.64 1.21
在误差允许的范围内单摆周期与摆长的平方成正比。
3. 单摆的周期公式
(2)国际单位:秒(s)
惠更斯
T = 2π
(1)周期公式:
荷兰物理学家惠更斯进行了详尽的研究,发现单摆做简谐运动的周期 T 与摆长 l 的二次方根成正比,与重力加速度 g 的二次方根成反比,而与振幅、摆球质量无关。
(3)单摆周期公式的应用和理解
周期公式的应用:由单摆周期公式可得g= ,只要测出单摆的摆长 l 和周期T就可算出当地的重力加速度。
由公式可知,某单摆做简谐运动(摆角小于5°)的周期只与其摆长 l 和当地的重力加速度 g 有关,而与振幅或摆球质量无关。摆长、重力加速度都一定时,周期和频率也一定,通常称为单摆的固有周期和固有频率。
实际的单摆摆球不可能是质点,所以摆长应是从悬点到摆球球心的长度,即 ,l1为摆线长,d为摆球直径。
思考:如果将单摆从赤道移到北京,周期会怎么变化?如果将单摆从海面移到高山,周期又会怎么变化?
如果将单摆从赤道移到北京,周期将变小
如果将单摆从海面移到高山,周期将变大
重力加速度g:由单摆所在的空间位置决定。
纬度越低,高度越高,g值就越小。
不同星球上g值也不同。
T =2
1.(多选)关于单摆摆球在运动过程中的受力,下列结论正确的是( )
A.摆球受重力、摆线的拉力作用
B.摆球受重力、摆线的拉力、回复力作用
C.摆球的回复力为零时,向心力最大
D.摆球的回复力最大时,摆线中的拉力大小比摆球的重力大
AC
2.图中O点为单摆的固定悬点,现将摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程( )
A.摆球在A点和C点处,速度为零,合力也为零
B.摆球在A点和C点处,速度为零,回复力也为零
C.摆球在B点处,速度最大,回复力也最大
D.摆球在B点处,速度最大,向心力也最大
D
3.一个单摆的摆长为,在其悬点O的正下方0.19处有一钉子P(如图所示),现将摆球向左拉开到A,使摆线偏角<5°,放手后使其摆动,摆动到B的过程中摆角也小于5°,求出单摆的振动周期。
解:释放后摆球到达右边最高点B处,由机械能守恒可知B和A等高,则摆球始终做简谐运动。
小球在左边的周期为T1=2π
小球在右边的周期为T2=2π
则整个单摆的周期为T=+=π+π=1.9π
单摆
单摆:
单摆的回复力:摆球重力沿切线方向的分力
单摆的周期:
理想化模型
