人教版(2019)选择性必修第三册 2.2 气体的等温变化 课件(共23张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修第三册 2.2 气体的等温变化 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
2.2 气体的等温变化
一定质量的气体,在温度不变的条件下,其压强与体积变化时的关系。我们把这种变化叫作气体的等温变化。
英国科学家玻意耳和法国科学家马略特各自通过实验发现,一定质量的某种气体,在温度不变的情况下,压强p与体积V 成反比,即
写成公式就是
C是常量
或者
反映了一定质量的某种气体的等温变化规律,我们把它叫作玻意耳定律
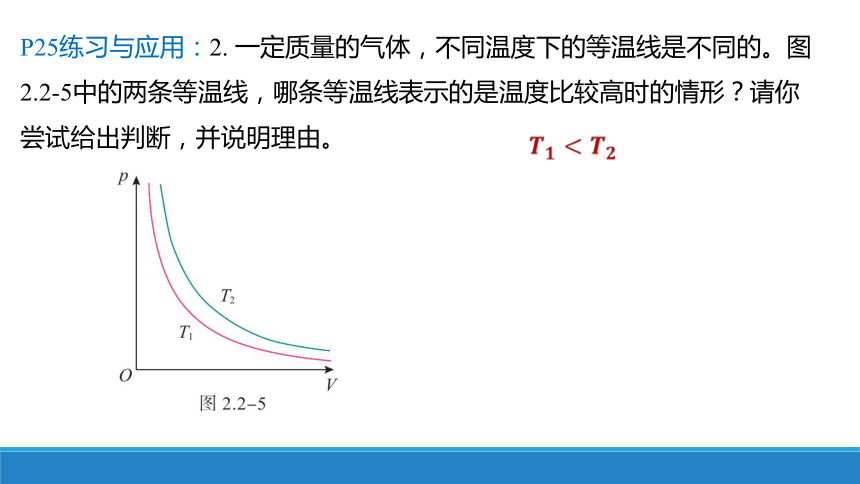
P25练习与应用:2. 一定质量的气体,不同温度下的等温线是不同的。图2.2-5中的两条等温线,哪条等温线表示的是温度比较高时的情形?请你尝试给出判断,并说明理由。
P25练习与应用: 3. 一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
温度不变
用气体定律解题的步骤
1.确定研究对象.被封闭的气体(满足质量不变的条件);
2.用一定的数字或表达式写出气体状态的初始条件(p1,V1,T1,p2,V2,T2);
3.根据气体状态变化过程的特点,列出相应的气体公式(本节课中就是玻意耳定律公式);
4.将各初始条件代入气体公式中,求解未知量;
5.对结果的物理意义进行讨论.
【随堂挑战1】容积为20L的钢瓶充满氧气后,压强为150atm,打开钢瓶的阀门让氧气同时分装到容积为1L的小瓶中,若小瓶原来是真空的,小瓶中充气后压强为10atm,分装过程中无漏气,且温度不变,那么最多能分装( )
A.15瓶 B.20瓶
C.280瓶 D.300瓶
C
考点一 封闭气体压强的计算
1.如图甲所示,C、D液面水平且等高,液体密度为ρ,重力加速度为g,大气压强为p0,其他条件已标于图上,试求封闭气体A的压强.
同一水平液面C、D处压强相同,可得pA=p0+ρgh.
思维点拨:液体中相同高度的位置压强相同;气体中各处压强相同
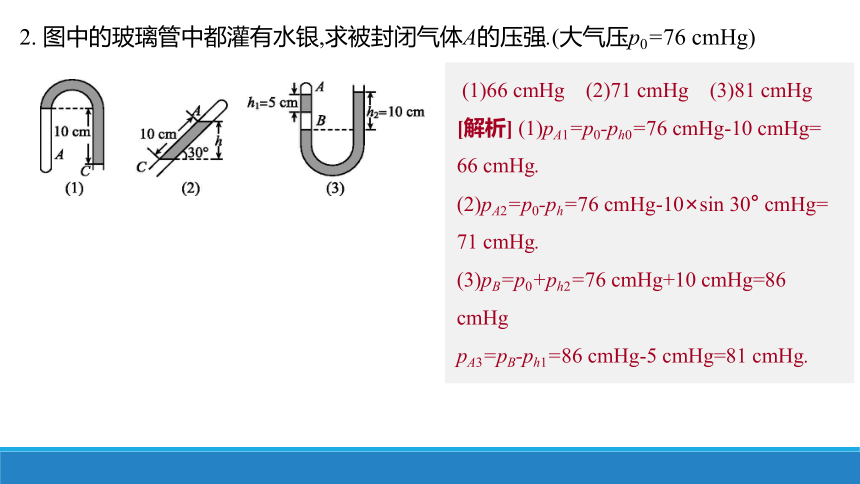
2. 图中的玻璃管中都灌有水银,求被封闭气体A的压强.(大气压p0=76 cmHg)
(1)66 cmHg (2)71 cmHg (3)81 cmHg
[解析] (1)pA1=p0-ph0=76 cmHg-10 cmHg=
66 cmHg.
(2)pA2=p0-ph=76 cmHg-10×sin 30° cmHg=
71 cmHg.
(3)pB=p0+ph2=76 cmHg+10 cmHg=86 cmHg
pA3=pB-ph1=86 cmHg-5 cmHg=81 cmHg.
3.在图乙中,汽缸置于水平地面上,汽缸横截面积为S,活塞质量为m,汽缸与活塞之间无摩擦,设大气压强为p0,重力加速度为g,试求封闭气体的压强.
以活塞为研究对象,受力分析如图所示,由平衡条件得
mg+p0S=pS,则
p=p0+.
考点二:玻意耳定律的应用
P25练习与应用: 4.水银气压计中混入了一个气泡,上升到水银柱的上方,使水银柱上方不再是真空。当实际大气压相当于768 mm高的水银柱产生的压强时,这个水银气压计的读数只有750 mm,此时管中的水银面到管顶的距离为80 mm。当这个气压计的读数为740 mm水银柱时,实际的大气压相当于多高水银柱产生的压强?设温度保持不变。
p1V1 = p2V2
P42复习与提高A组:2. 如图 2-1,某自动洗衣机洗衣缸的下部与一控水装置的竖直均匀细管相通,细管的上部封闭,并和一压力传感器相接。洗衣缸进水时,细管中的空气被水封闭,随着洗衣缸中水面的升高,细管中的空气被压缩,当细管中空气压强达到一定数值时,压力传感器使进水阀门关闭,达到自动控水的目的。假设刚进水时细管被封闭的空气柱长度为 50 cm,当空气柱被压缩到 48 cm 时压力传感器使洗衣机停止进水,此时洗衣缸内水位有多高?大气压取 105Pa,g取 10m/s2 。
0.44m
P42复习与提高A组: 3. 今有一质量为 m 的汽缸,用活塞封着一定质量的理想气体,当汽缸水平横放时,汽缸内空气柱长为 l0 (如图 2-2 甲所示),现把活塞按如图乙那样悬挂,汽缸悬在空中保持静止。求此时汽缸内空气柱长度为多少?已知大气压强为 p0 ,活塞的横截面积为 S,它与汽缸之间无摩擦且不漏气,气体温度保持不变。
用气体定律解题的步骤
1.确定研究对象.被封闭的气体(满足质量不变的条件);
2.用一定的数字或表达式写出气体状态的初始条件(p1,V1,T1,p2,V2,T2);
3.根据气体状态变化过程的特点,列出相应的气体公式(本节课中就是玻意耳定律公式);
4.将各初始条件代入气体公式中,求解未知量;
5.对结果的物理意义进行讨论.
【拓展提升1】如图所示是一定质量的某种气体状态变化的p-V图像,气体由状态A变化到状态B的过程中,气体分子平均速率的变化情况是( )
A.一直保持不变 B.一直增大
C.先减小后增大 D.先增大后减小
D
某个容器的容积是10L,所装气体的压强是20×105Pa。如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1.0×105Pa。
解 设容器原装气体为研究对象。
初态 p1=20×105Pa V1=10L T1=T
末态 p2=1.0×105Pa V2=?L T2=T
由玻意耳定律 p1V1=p2V2得
即剩下的气体为原来的5%。
就容器而言,里面气体质量变了,似乎是变质量问题了,但若视容器中气体出而不走,就又是质量不变了。
变质量问题
【拓展提升2】
如图所示,下端用橡皮管连接的两根粗细相同的玻璃管均竖直放置,右管上端开口,水银面到管口距离较长,左管内封闭一段气体,水银面比右管稍低.现保持左管不动,为了使两管内水银面最终一样高,下面采取的措施可行的是(以下各种措施中,右管始终没有水银溢出)( )
A.仅减小外界气压 B.仅把U形管的右管向下移动
C.仅把U形管的右管向上移动 D.仅向U形管的右管内加水银
B
考点二:玻意耳定律的应用
一个U形玻璃管竖直放置,左端开口,右端封闭,玻璃管导热性能良好.在右管中用水银封闭一段空气柱,初始时,管内水银柱及空气柱长度如图甲所示.将玻璃管在竖直平面内旋转90°,如图乙所示.求此时右管中水银面移动的距离.(已知玻璃管的横截面积处处相同,大气压强p0=76.0 cmHg,环境温度不变,管的直径忽略不计)
考点二:玻意耳定律的应用
[答案] 0.5 cm
[解析] 以右管空气为研究对象,则初态:
p1=p0-ph1=(76-4) cmHg=72 cmHg,V1=SL1=S·5 cm
末态:p2=p0+ph2=(76+4) cmHg=80 cmHg,
V2=SL2
由玻意耳定律得p1V1=p2V2
解得L2=4.5 cm
故右管中水银面移动的距离x=L1-L2=0.5 cm
将一端封闭的均匀直玻璃管开口向下,竖直插入水银中,当管顶距槽中水银面8cm时,管内水银面比管外水银面低2cm.要使管内水银面比管外水银面高2cm,应将玻璃管竖直向上提起多少厘米?已知大气压强p0支持76cmHg,设温度不变.
解:根据题意,由图知
p1=p0+2cmHg=78cmHg,V1=(8+2)S=10S,
p2=p0-2cmHg=74cmHg,
V2=[(8+x)-2]·S=(6+x)S.
根据玻意耳定律:
78×10=74×(6+x)
得到玻璃管提升高的高度:
X≈4.54cm
P44复习与提高B组:6. 细长玻璃管用长 l0 为 6.8cm 的水银柱封闭一定质量的空气。当玻璃管开口向下竖直放置时,空气柱长度 l1 为 33 cm ;当玻璃管水平放置时,空气柱长度 l2 为 30cm。求玻璃管开口向上竖直放置时空气柱的长度。
27.5cm
以玻璃管中封闭的空气为研究对象,它经历等温变化
设水银的密度为,玻璃管的横截面积为,大气压强为(相当于76cm水银产生的压强)
开口向下时:
水平放置时:
开口向上时:
由玻意耳定律,有
代入数据,解得
2.2 气体的等温变化
一定质量的气体,在温度不变的条件下,其压强与体积变化时的关系。我们把这种变化叫作气体的等温变化。
英国科学家玻意耳和法国科学家马略特各自通过实验发现,一定质量的某种气体,在温度不变的情况下,压强p与体积V 成反比,即
写成公式就是
C是常量
或者
反映了一定质量的某种气体的等温变化规律,我们把它叫作玻意耳定律
P25练习与应用:2. 一定质量的气体,不同温度下的等温线是不同的。图2.2-5中的两条等温线,哪条等温线表示的是温度比较高时的情形?请你尝试给出判断,并说明理由。
P25练习与应用: 3. 一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
温度不变
用气体定律解题的步骤
1.确定研究对象.被封闭的气体(满足质量不变的条件);
2.用一定的数字或表达式写出气体状态的初始条件(p1,V1,T1,p2,V2,T2);
3.根据气体状态变化过程的特点,列出相应的气体公式(本节课中就是玻意耳定律公式);
4.将各初始条件代入气体公式中,求解未知量;
5.对结果的物理意义进行讨论.
【随堂挑战1】容积为20L的钢瓶充满氧气后,压强为150atm,打开钢瓶的阀门让氧气同时分装到容积为1L的小瓶中,若小瓶原来是真空的,小瓶中充气后压强为10atm,分装过程中无漏气,且温度不变,那么最多能分装( )
A.15瓶 B.20瓶
C.280瓶 D.300瓶
C
考点一 封闭气体压强的计算
1.如图甲所示,C、D液面水平且等高,液体密度为ρ,重力加速度为g,大气压强为p0,其他条件已标于图上,试求封闭气体A的压强.
同一水平液面C、D处压强相同,可得pA=p0+ρgh.
思维点拨:液体中相同高度的位置压强相同;气体中各处压强相同
2. 图中的玻璃管中都灌有水银,求被封闭气体A的压强.(大气压p0=76 cmHg)
(1)66 cmHg (2)71 cmHg (3)81 cmHg
[解析] (1)pA1=p0-ph0=76 cmHg-10 cmHg=
66 cmHg.
(2)pA2=p0-ph=76 cmHg-10×sin 30° cmHg=
71 cmHg.
(3)pB=p0+ph2=76 cmHg+10 cmHg=86 cmHg
pA3=pB-ph1=86 cmHg-5 cmHg=81 cmHg.
3.在图乙中,汽缸置于水平地面上,汽缸横截面积为S,活塞质量为m,汽缸与活塞之间无摩擦,设大气压强为p0,重力加速度为g,试求封闭气体的压强.
以活塞为研究对象,受力分析如图所示,由平衡条件得
mg+p0S=pS,则
p=p0+.
考点二:玻意耳定律的应用
P25练习与应用: 4.水银气压计中混入了一个气泡,上升到水银柱的上方,使水银柱上方不再是真空。当实际大气压相当于768 mm高的水银柱产生的压强时,这个水银气压计的读数只有750 mm,此时管中的水银面到管顶的距离为80 mm。当这个气压计的读数为740 mm水银柱时,实际的大气压相当于多高水银柱产生的压强?设温度保持不变。
p1V1 = p2V2
P42复习与提高A组:2. 如图 2-1,某自动洗衣机洗衣缸的下部与一控水装置的竖直均匀细管相通,细管的上部封闭,并和一压力传感器相接。洗衣缸进水时,细管中的空气被水封闭,随着洗衣缸中水面的升高,细管中的空气被压缩,当细管中空气压强达到一定数值时,压力传感器使进水阀门关闭,达到自动控水的目的。假设刚进水时细管被封闭的空气柱长度为 50 cm,当空气柱被压缩到 48 cm 时压力传感器使洗衣机停止进水,此时洗衣缸内水位有多高?大气压取 105Pa,g取 10m/s2 。
0.44m
P42复习与提高A组: 3. 今有一质量为 m 的汽缸,用活塞封着一定质量的理想气体,当汽缸水平横放时,汽缸内空气柱长为 l0 (如图 2-2 甲所示),现把活塞按如图乙那样悬挂,汽缸悬在空中保持静止。求此时汽缸内空气柱长度为多少?已知大气压强为 p0 ,活塞的横截面积为 S,它与汽缸之间无摩擦且不漏气,气体温度保持不变。
用气体定律解题的步骤
1.确定研究对象.被封闭的气体(满足质量不变的条件);
2.用一定的数字或表达式写出气体状态的初始条件(p1,V1,T1,p2,V2,T2);
3.根据气体状态变化过程的特点,列出相应的气体公式(本节课中就是玻意耳定律公式);
4.将各初始条件代入气体公式中,求解未知量;
5.对结果的物理意义进行讨论.
【拓展提升1】如图所示是一定质量的某种气体状态变化的p-V图像,气体由状态A变化到状态B的过程中,气体分子平均速率的变化情况是( )
A.一直保持不变 B.一直增大
C.先减小后增大 D.先增大后减小
D
某个容器的容积是10L,所装气体的压强是20×105Pa。如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1.0×105Pa。
解 设容器原装气体为研究对象。
初态 p1=20×105Pa V1=10L T1=T
末态 p2=1.0×105Pa V2=?L T2=T
由玻意耳定律 p1V1=p2V2得
即剩下的气体为原来的5%。
就容器而言,里面气体质量变了,似乎是变质量问题了,但若视容器中气体出而不走,就又是质量不变了。
变质量问题
【拓展提升2】
如图所示,下端用橡皮管连接的两根粗细相同的玻璃管均竖直放置,右管上端开口,水银面到管口距离较长,左管内封闭一段气体,水银面比右管稍低.现保持左管不动,为了使两管内水银面最终一样高,下面采取的措施可行的是(以下各种措施中,右管始终没有水银溢出)( )
A.仅减小外界气压 B.仅把U形管的右管向下移动
C.仅把U形管的右管向上移动 D.仅向U形管的右管内加水银
B
考点二:玻意耳定律的应用
一个U形玻璃管竖直放置,左端开口,右端封闭,玻璃管导热性能良好.在右管中用水银封闭一段空气柱,初始时,管内水银柱及空气柱长度如图甲所示.将玻璃管在竖直平面内旋转90°,如图乙所示.求此时右管中水银面移动的距离.(已知玻璃管的横截面积处处相同,大气压强p0=76.0 cmHg,环境温度不变,管的直径忽略不计)
考点二:玻意耳定律的应用
[答案] 0.5 cm
[解析] 以右管空气为研究对象,则初态:
p1=p0-ph1=(76-4) cmHg=72 cmHg,V1=SL1=S·5 cm
末态:p2=p0+ph2=(76+4) cmHg=80 cmHg,
V2=SL2
由玻意耳定律得p1V1=p2V2
解得L2=4.5 cm
故右管中水银面移动的距离x=L1-L2=0.5 cm
将一端封闭的均匀直玻璃管开口向下,竖直插入水银中,当管顶距槽中水银面8cm时,管内水银面比管外水银面低2cm.要使管内水银面比管外水银面高2cm,应将玻璃管竖直向上提起多少厘米?已知大气压强p0支持76cmHg,设温度不变.
解:根据题意,由图知
p1=p0+2cmHg=78cmHg,V1=(8+2)S=10S,
p2=p0-2cmHg=74cmHg,
V2=[(8+x)-2]·S=(6+x)S.
根据玻意耳定律:
78×10=74×(6+x)
得到玻璃管提升高的高度:
X≈4.54cm
P44复习与提高B组:6. 细长玻璃管用长 l0 为 6.8cm 的水银柱封闭一定质量的空气。当玻璃管开口向下竖直放置时,空气柱长度 l1 为 33 cm ;当玻璃管水平放置时,空气柱长度 l2 为 30cm。求玻璃管开口向上竖直放置时空气柱的长度。
27.5cm
以玻璃管中封闭的空气为研究对象,它经历等温变化
设水银的密度为,玻璃管的横截面积为,大气压强为(相当于76cm水银产生的压强)
开口向下时:
水平放置时:
开口向上时:
由玻意耳定律,有
代入数据,解得
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
