1.5 弹性碰撞和非弹性碰撞(共23张PPT)课件 2024-2025学年高二物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 1.5 弹性碰撞和非弹性碰撞(共23张PPT)课件 2024-2025学年高二物理人教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-23 16:54:16 | ||
图片预览








文档简介
(共23张PPT)
第一章 动量守恒定律
第5节 弹性碰撞和非弹性碰撞
碰撞是自然界常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……
物体碰撞中动量的变化情况,前面已进行了研究。那么,在各种碰撞中能量又是如何变化的?
1.了解弹性碰撞、非弹性碰撞。
2.会分析具体实例中的碰撞特点及类型。
3.能利用动量和能量的观点解决生产生活中与一维碰撞相关的实际问题。
01 弹性碰撞与非弹性碰撞
回顾:本章第一节的实验:两小车的质量分别为m1和m2,v是运动小车m1 碰撞前的速度,v'是碰撞后两辆小车的共同速度。比较碰撞前后两辆小车总动能情况。
利用实验数据计算得:Ek>Ek′
思考:若是带弹性碰撞架小车的碰撞,碰撞前后系统动能又是如何变化的?
碰前总动能:Ek=
0
碰后总动能:Ek′=
0
装置:如图,两辆安装了弹性碰撞架的小车置于滑轨上,测量两辆小车的质量以及它们碰撞前后的速度。
目的:研究碰撞前后总动能的变化情况。
实验:研究小车碰撞前后的动能变化
⑴总动能减少的原因是什么?
⑶需要测量哪些实验数据?如何测量?
⑵为减少总动能的损失,怎么改进实验装置?
思考:
视频:研究小车碰撞前后的动能变化
结论:
在该实验条件下,碰撞前后系统动能基本不变。
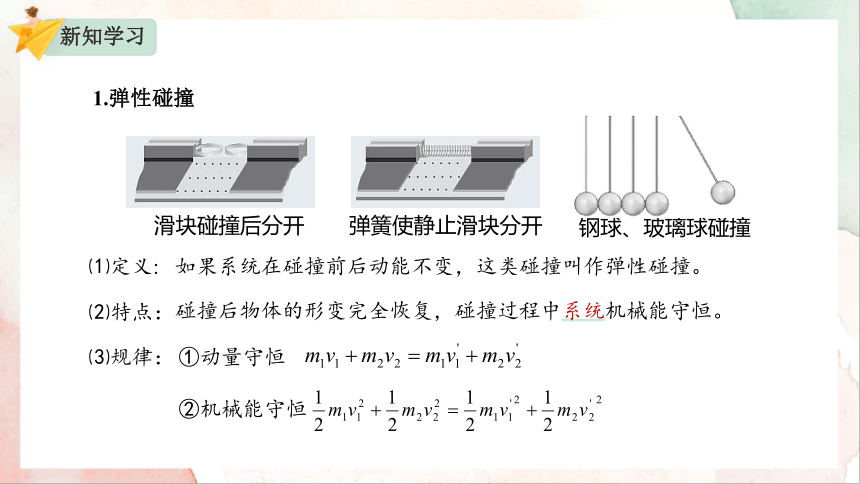
1.弹性碰撞
碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
⑵特点:
⑴定义:
①动量守恒
②机械能守恒
⑶规律:
滑块碰撞后分开
弹簧使静止滑块分开
钢球、玻璃球碰撞
2.非弹性碰撞
①动量守恒:
②机械能不守恒:
实例:木制品、橡皮泥球的碰撞
⑴定义:
⑵特点:
碰撞后不能完全恢复形变,碰撞过程中系统机械能减少。
如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
⑶规律:
3.完全非弹性碰撞——非弹性碰撞特例
实例:碰后粘在一起运动
②机械能不守恒
(机械能损失:⊿E损=Ek总初-Ek总末)
①动量守恒
⑴定义:
系统机械能损失最大。
碰撞后粘合在一起,以共同速度运动(或碰后具有共同的速度)。
⑵特点:
⑶规律
例题1 在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v0 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m的物体,以一定的速度继续前进,碰撞后该系统的总动能是否会有损失?
v0
静止
m
m
v
2m
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
可见碰撞过程有机械能损失。
解析:
⑴时间特点:
⑵作用力特点:
⑶位移特点:
⑷系统动量特点:
碰撞的特点
Ek1≥Ek2
将碰撞双方包括在同一系统内,系统的总动量(近似)守恒。
可以认为碰撞前后,物体仍在原来的位置(即位移不变),其它与碰撞物体相联系,但不直接参与碰撞的物体,其运动状态仍保持不变。
在碰撞过程中,相互作用力即内力先急剧增大,后急剧减小,平均作用力很大。
在碰撞过程中,相互作用时间很短(⊿t→0) 。
⑸系统能量特点:
v1
v2
碰撞前后的速度不在一条直线,也称斜碰。
m2
m1
v′2
v′1
m2
m1
v1
碰撞前
碰撞后
斜碰(非对心碰撞)
正碰:碰撞之前球的运动方向与两球心的连线在同一条直线上。又称对心碰撞,或称一维碰撞。
什么是正碰与斜碰?
02 弹性碰撞的实例分析
v1
v2=0
水平光滑
①
②
由①②可得
思考: 方程组该怎样快速求解?
由动量守恒有
由机械能守恒有
【分析】
“一动一静”的基本规律
讨论:
⑴ m1 > m2 时,有
m1
m2
v1
若 m1 >> m2,碰后有
v1′= 0, v2′= v1 即碰后速度交换。
v1′=-v1 v2′= 0
⑵ m1=m2时,有
⑶ m1 < m2时,有
m1
m2
v1
v1′> 0,v2′> 0,即碰后同向。
v1′< 0, v2′>0 碰后反向。
取m1碰前速度方向为正方向。
若m1 << m2,碰后有
思考:若v2=0时,结论与前面的是否相同?
由动量守恒有
由机械能守恒有
“动碰动”的基本规律
v1
v2
水平光滑
v1>v2
例题2 在光滑的水平面上,有A、B两球沿同一直线向右运动如图。已知碰撞前两球的动量分别为:pA=12 kg·m/s,pB=13 kg·m/s。碰撞后它们的动量变化是ΔpA、ΔpB 有可能的是 ( )
A.ΔpA=-3kg·m/s, ΔpB=3 kg·m/s.
B.ΔpA=4kg·m/s, ΔpB=-4 kg·m/s.
C.ΔpA=-5 kg·m/s, ΔpB=5 kg·m/s.
D.ΔpA=-24kg·m/s, ΔpB=24 kg·m/s.
AC
pA
A
B
pB
解决碰撞问题遵守的三个原则
思考:满足动量守恒定律的碰撞一定能实现吗?为什么?
3.符合实际情境
碰撞前:
碰撞后:若仍同向,则
2.动能不增加的原则
1.系统动量守恒原则
实例:⑴追赶碰撞
p1+p2=p1′+p2′
Ek1+Ek2≥Ek1′+Ek2′
⑵相向碰撞:
碰后至少有一个物体要反向。
或者
小结:解决碰撞问题遵守的三个原则
1.(多选)在光滑水平面上,两球沿球心连线以相等速率相向而行,并发生碰撞,下列现象可能的是 ( )
A.若两球质量相等,碰后以某一相等速率互相分开
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不等,碰后以某一相等速率互相分开
D.若两球质量不等,碰后以某一相等速率同向而行
AD
2.在光滑的水平面上有A、B两球,其质量分别为mA、mB,两球在t0时刻发生正碰,并且在碰撞过程中无机械能损失,两球在碰撞前后的速度—时间图象如图所示,下列关系式正确的是( )
A.mA>mB
B.mAC.mA=mB
D.无法判断
B
3.两球A、B在光滑水平面上沿同一直线、同一方向运动,mA=1 kg,mB=2 kg,vA=6 m/s,vB=2 m/s,当球A追上B并发生碰撞后,两球A、B速度的可能值是(取两球碰撞前的运动方向为正)( )
A.vA′=5 m/s,vB′=2.5 m/s
B.vA′=2 m/s,vB′=4 m/s
C.vA′=-4 m/s,vB′=7 m/s
D.vA′=7 m/s,vB′= 1.5 m/s
B
4.一轻质弹簧的两端连接两滑块A和B,已知mA=0.99 kg,mB=3 kg,放在光滑水平面上,开始时弹簧处于原长,现滑块A被水平飞来的质量为mC=10 g,速度为400 m/s的子弹击中,且没有穿出,如图所示。求:
⑴子弹击中滑块A的瞬间滑块A和B的速度;
⑵以后运动过程中弹簧的最大弹性势能。
解:(1)子弹击中滑块A的过程中,子弹与滑块A组成的系统动量守恒,设共同速度vA,取子弹开始运动方向为正方向,有
滑块A在此过程中无位移,弹簧无形变,滑块B仍静止,即vB=0。
(2)对子弹、滑块A、B和弹簧组成的系统,当滑块A、B速度相等时弹簧的弹性势能最大,根据动量守恒和机械能守恒,有
mC v0=(mA+mC)vA,
mC v0=(mA+mB+mC )v,解得
1.弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
4.对心碰撞和非对心碰撞
2.非弹性碰撞:碰撞过程中机械能减小,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒、机械能减小
(2) 能量转化情况:系统动能损失
3.完全非弹性碰撞:碰撞后两物体连在一起运动的现象。
第一章 动量守恒定律
第5节 弹性碰撞和非弹性碰撞
碰撞是自然界常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……
物体碰撞中动量的变化情况,前面已进行了研究。那么,在各种碰撞中能量又是如何变化的?
1.了解弹性碰撞、非弹性碰撞。
2.会分析具体实例中的碰撞特点及类型。
3.能利用动量和能量的观点解决生产生活中与一维碰撞相关的实际问题。
01 弹性碰撞与非弹性碰撞
回顾:本章第一节的实验:两小车的质量分别为m1和m2,v是运动小车m1 碰撞前的速度,v'是碰撞后两辆小车的共同速度。比较碰撞前后两辆小车总动能情况。
利用实验数据计算得:Ek>Ek′
思考:若是带弹性碰撞架小车的碰撞,碰撞前后系统动能又是如何变化的?
碰前总动能:Ek=
0
碰后总动能:Ek′=
0
装置:如图,两辆安装了弹性碰撞架的小车置于滑轨上,测量两辆小车的质量以及它们碰撞前后的速度。
目的:研究碰撞前后总动能的变化情况。
实验:研究小车碰撞前后的动能变化
⑴总动能减少的原因是什么?
⑶需要测量哪些实验数据?如何测量?
⑵为减少总动能的损失,怎么改进实验装置?
思考:
视频:研究小车碰撞前后的动能变化
结论:
在该实验条件下,碰撞前后系统动能基本不变。
1.弹性碰撞
碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
⑵特点:
⑴定义:
①动量守恒
②机械能守恒
⑶规律:
滑块碰撞后分开
弹簧使静止滑块分开
钢球、玻璃球碰撞
2.非弹性碰撞
①动量守恒:
②机械能不守恒:
实例:木制品、橡皮泥球的碰撞
⑴定义:
⑵特点:
碰撞后不能完全恢复形变,碰撞过程中系统机械能减少。
如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
⑶规律:
3.完全非弹性碰撞——非弹性碰撞特例
实例:碰后粘在一起运动
②机械能不守恒
(机械能损失:⊿E损=Ek总初-Ek总末)
①动量守恒
⑴定义:
系统机械能损失最大。
碰撞后粘合在一起,以共同速度运动(或碰后具有共同的速度)。
⑵特点:
⑶规律
例题1 在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v0 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m的物体,以一定的速度继续前进,碰撞后该系统的总动能是否会有损失?
v0
静止
m
m
v
2m
由动量守恒定律:
碰撞前系统总动能:
碰撞后系统总动能:
可见碰撞过程有机械能损失。
解析:
⑴时间特点:
⑵作用力特点:
⑶位移特点:
⑷系统动量特点:
碰撞的特点
Ek1≥Ek2
将碰撞双方包括在同一系统内,系统的总动量(近似)守恒。
可以认为碰撞前后,物体仍在原来的位置(即位移不变),其它与碰撞物体相联系,但不直接参与碰撞的物体,其运动状态仍保持不变。
在碰撞过程中,相互作用力即内力先急剧增大,后急剧减小,平均作用力很大。
在碰撞过程中,相互作用时间很短(⊿t→0) 。
⑸系统能量特点:
v1
v2
碰撞前后的速度不在一条直线,也称斜碰。
m2
m1
v′2
v′1
m2
m1
v1
碰撞前
碰撞后
斜碰(非对心碰撞)
正碰:碰撞之前球的运动方向与两球心的连线在同一条直线上。又称对心碰撞,或称一维碰撞。
什么是正碰与斜碰?
02 弹性碰撞的实例分析
v1
v2=0
水平光滑
①
②
由①②可得
思考: 方程组该怎样快速求解?
由动量守恒有
由机械能守恒有
【分析】
“一动一静”的基本规律
讨论:
⑴ m1 > m2 时,有
m1
m2
v1
若 m1 >> m2,碰后有
v1′= 0, v2′= v1 即碰后速度交换。
v1′=-v1 v2′= 0
⑵ m1=m2时,有
⑶ m1 < m2时,有
m1
m2
v1
v1′> 0,v2′> 0,即碰后同向。
v1′< 0, v2′>0 碰后反向。
取m1碰前速度方向为正方向。
若m1 << m2,碰后有
思考:若v2=0时,结论与前面的是否相同?
由动量守恒有
由机械能守恒有
“动碰动”的基本规律
v1
v2
水平光滑
v1>v2
例题2 在光滑的水平面上,有A、B两球沿同一直线向右运动如图。已知碰撞前两球的动量分别为:pA=12 kg·m/s,pB=13 kg·m/s。碰撞后它们的动量变化是ΔpA、ΔpB 有可能的是 ( )
A.ΔpA=-3kg·m/s, ΔpB=3 kg·m/s.
B.ΔpA=4kg·m/s, ΔpB=-4 kg·m/s.
C.ΔpA=-5 kg·m/s, ΔpB=5 kg·m/s.
D.ΔpA=-24kg·m/s, ΔpB=24 kg·m/s.
AC
pA
A
B
pB
解决碰撞问题遵守的三个原则
思考:满足动量守恒定律的碰撞一定能实现吗?为什么?
3.符合实际情境
碰撞前:
碰撞后:若仍同向,则
2.动能不增加的原则
1.系统动量守恒原则
实例:⑴追赶碰撞
p1+p2=p1′+p2′
Ek1+Ek2≥Ek1′+Ek2′
⑵相向碰撞:
碰后至少有一个物体要反向。
或者
小结:解决碰撞问题遵守的三个原则
1.(多选)在光滑水平面上,两球沿球心连线以相等速率相向而行,并发生碰撞,下列现象可能的是 ( )
A.若两球质量相等,碰后以某一相等速率互相分开
B.若两球质量相等,碰后以某一相等速率同向而行
C.若两球质量不等,碰后以某一相等速率互相分开
D.若两球质量不等,碰后以某一相等速率同向而行
AD
2.在光滑的水平面上有A、B两球,其质量分别为mA、mB,两球在t0时刻发生正碰,并且在碰撞过程中无机械能损失,两球在碰撞前后的速度—时间图象如图所示,下列关系式正确的是( )
A.mA>mB
B.mA
D.无法判断
B
3.两球A、B在光滑水平面上沿同一直线、同一方向运动,mA=1 kg,mB=2 kg,vA=6 m/s,vB=2 m/s,当球A追上B并发生碰撞后,两球A、B速度的可能值是(取两球碰撞前的运动方向为正)( )
A.vA′=5 m/s,vB′=2.5 m/s
B.vA′=2 m/s,vB′=4 m/s
C.vA′=-4 m/s,vB′=7 m/s
D.vA′=7 m/s,vB′= 1.5 m/s
B
4.一轻质弹簧的两端连接两滑块A和B,已知mA=0.99 kg,mB=3 kg,放在光滑水平面上,开始时弹簧处于原长,现滑块A被水平飞来的质量为mC=10 g,速度为400 m/s的子弹击中,且没有穿出,如图所示。求:
⑴子弹击中滑块A的瞬间滑块A和B的速度;
⑵以后运动过程中弹簧的最大弹性势能。
解:(1)子弹击中滑块A的过程中,子弹与滑块A组成的系统动量守恒,设共同速度vA,取子弹开始运动方向为正方向,有
滑块A在此过程中无位移,弹簧无形变,滑块B仍静止,即vB=0。
(2)对子弹、滑块A、B和弹簧组成的系统,当滑块A、B速度相等时弹簧的弹性势能最大,根据动量守恒和机械能守恒,有
mC v0=(mA+mC)vA,
mC v0=(mA+mB+mC )v,解得
1.弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
4.对心碰撞和非对心碰撞
2.非弹性碰撞:碰撞过程中机械能减小,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒、机械能减小
(2) 能量转化情况:系统动能损失
3.完全非弹性碰撞:碰撞后两物体连在一起运动的现象。
