北京市海淀区一零一中学2024-2025学年七年级上学期入学分班考试数学卷(PDF版,含答案)
文档属性
| 名称 | 北京市海淀区一零一中学2024-2025学年七年级上学期入学分班考试数学卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 607.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-24 19:10:41 | ||
图片预览




文档简介
北京市-海淀区-一零一中学 2024-2025学年七年级上学期入学分班考试数学卷
一、填空题
1 1 1甲数的 与乙数的 相等,甲数的 25%与丙数的 20%相等.那么,甲、乙、丙的大小顺序是 .
5 4
2 1如图,将 10毫升酒装入一个圆锥形容器中,酒深正好占容器深的 .请问:再添入 毫升酒,可
2
装满此容器?
3 瓷器商店托快递公司送 800只瓷花瓶,双方约定每只运费是 3角 5分,若打破 1只,这只不但不给运费
还要赔偿 2元 5角钱.结果运到目的地后,快递公司共得运费 268.6元.在搬运过程中,打破了 只
花瓶.
4 将图甲围成图形乙的正方体,则在面①CDHE;②BCEF;③ABFG;④ADHG中,图甲中的“ 红心标
志所在的正方形是正方体中的面 .(填序号)
1011
5 小牛和爷爷、奶奶 8月 5日从北京出发,7日到 10日在南京旅游,8月 11日返回北京,北京与南京间的
火车和飞机票价如下:
交通工具 票价(元) 备注
飞机(普通舱) 1160 元 已满2周岁未满 l2周岁的儿童享受半价票
火车(硬卧) 290 元 身高1.1-1.4米的儿童享受半价票
他们在南京主要开支预算有以下几项:
住宿 伙食 市内交通 旅游景点门票
每日140元 每日90元 每日60元 每人 240元
小牛身高 1.38米,年龄 13周岁,他们准备了 6500元,去时乘坐火车,返回时乘坐飞机,照上面预计的开支,
他们大约还能剩余 元?
6 小明在一个正方形的棋盘里摆棋子,他先把最外层摆满,用了 40颗棋子,如果他要把整个棋盘摆满,还
需要 颗棋子.
7 甲、乙、丙、丁、戊五位同学在一次数学竞赛中得了前五名,发奖前老师要他们猜一猜各人所得的名次.
甲猜:乙第三名、丙第五名;
乙猜:戊第四名、丁第五名;
丙猜:甲第一名、戊第四名;
丁猜:丙第一名、乙第二名;
戊猜:甲第三名、丁第四名.
老师说:每个名次都有人猜对了,那么,获得第四名的是 .
二、选择题
8 5 5如果 a a,那么 a是( )
29 29
A.真分数 B.假分数 C.1 D.自然数
9 在圆中作一个最大的正方形,圆面积与正方形的面积之比是( )
A.2︰π B.π︰2 C.4︰3 D.4︰1
10 某班统计数学考试成绩,平均分是 84.2分,后来发现小明的成绩是 97分,而错误地统计为 79分,重新
计算后,平均成绩是 84.6分,则这个班的学生人数是( )
A.42 B.43 C.44 D.45
11 雷达二维平面定位的主要原理是:测量目标的两个信息——距离和角度,目标的表达方法为(y,a),其
中:y表示目标与探测器的距离;a表示以正东为始边,逆时针旋转的角度.如图,雷达探测器显示在点 A,
B,C处有目标出现,其中目标 A的位置表示为(5,30°),目标 B的位置表示为 B(4,150°).用这种方法
表示目标 C的位置,正确的是( )
A.(-3,300°) B.(3,60°)
C.(3,300°) D.(-3,60°)
12 已知一条直线 l和直线外的 A、B两点,以 A、B两点和直线上某一点做为三角形的三个顶点,就能画出
一个等腰三角形,如图中的等腰三角形 ABC.除此之外还能画出符合条件的等腰三角形个数是( )
A.1 B.2 C.3 D.4
13 在小红去培训班的路上,看到在一条公路上,每隔 100千米有一个仓库,共有五个仓库.A号仓库存有
10吨货物,B号仓库存有 20吨货物,E号仓库存有 40吨货物,其余两个仓是空的.现在想把所有的货物集
中存放在任意一个仓库里,如果每吨货物运输 1千米需要 1元运费,那么放在哪个仓库才能使运费最少?
( )
A.仓库 E B.仓库 D C.仓库 C D.仓库 B
12
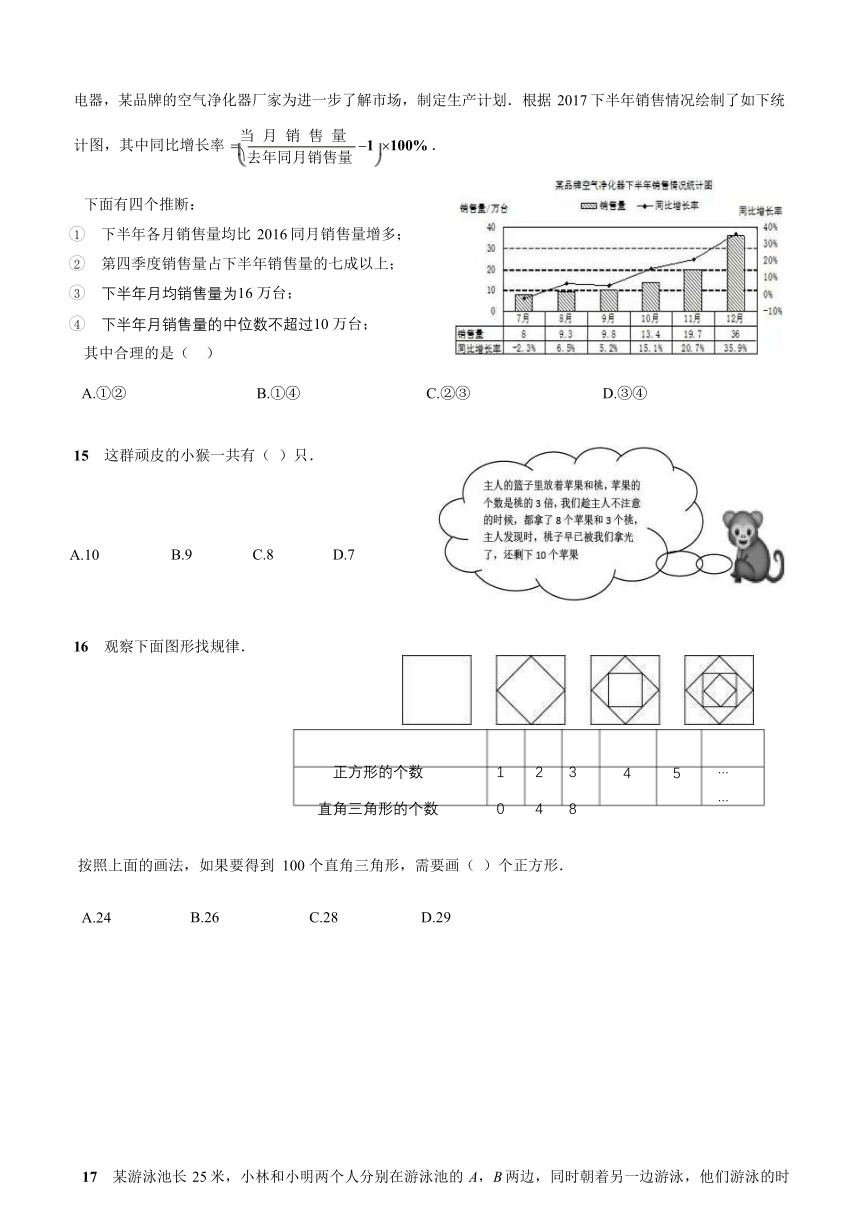
14 近年来由于空气质量的变化,以及人们对自身健康的关注程度不断提高,空气净化器成为很多家庭的新
电器,某品牌的空气净化器厂家为进一步了解市场,制定生产计划.根据 2017下半年销售情况绘制了如下统
当 月 销 售 量
计图,其中同比增长率 1 100%.
去年同月销售量
下面有四个推断:
1 下半年各月销售量均比 2016同月销售量增多;
2 第四季度销售量占下半年销售量的七成以上;
3 下半年月均销售量为16万台;
4 下半年月销售量的中位数不超过10万台;
其中合理的是( )
A.①② B.①④ C.②③ D.③④
15 这群顽皮的小猴一共有( )只.
A.10 B.9 C.8 D.7
16 观察下面图形找规律.
正方形的个数 1 2 3 4 5 …
直角三角形的个数 0 4 8 …
按照上面的画法,如果要得到 100个直角三角形,需要画( )个正方形.
A.24 B.26 C.28 D.29
13
17 某游泳池长 25米,小林和小明两个人分别在游泳池的 A,B两边,同时朝着另一边游泳,他们游泳的时
间为 t(秒),其中 0≤t≤180,到 A边距离为 y(米),图中的实线和虚线分别表示小林和小明在游泳过程中 y
和 t的对应关系.下面有四个推断:
1 ①小明游泳的平均速度小于小林游泳的平均速度;
2 ②小明游泳的距离大于小林游泳的距离;
3 小明游75米时小林游了 90米;
4 小明与小林共相遇5次.
其中正确的是()
A.①② B.①③ C.③④ D.②④
三、计算题
18 计算
(2)(12345+23451+34512+45123+51234)+(1+2+3+4+5)
1415
四、解答题
19
(1)利用下面网格,画一个钝角三角形 ABC,其中 AB=AC,顶点 ABC都在格点上;
(2)画出三角形 ABC一条腰上的高;
(3)再找出两个格点 E、F使得三角形 EBC与三角形 ABC面积相等、形状相同,使得三角形 FBC与三角形
ABC面积相等、形状不同.
20 阅读所给材料,并解答问题.
正数和负数是表示两种具有相反意义的量.如:胜与负、收入与支出、零上温度与零下温度、海平面以上与
海平面以下、东与西、升与降等.这些都是具有相反意义的量,因此可以用正、负数来表示它们.例如:若
规定向东走 200米记作+200米,则向西走 300米记作-300米;反之,若规定向西走 300米记作+300米,
则向东走 200米记作-200.
根据上述材料,回答下列问题:
出租车司机小王某天下午的营运全是在东西走向的人民大道上行驶的.如果规定向东为正,向西为负,他这
天下午行车里程如下:(单位:千米)
+15 -3 +14 -11 +10 -12 -4 +15 +16 -18
(1)将最后一名乘客送到目的地时,小王距下午出车地点的距离是多少千米?
(2)若汽车耗油率为 2.5升/千米,则这天下午汽车共耗油多少升?
1516
21 下图为 2018年 1月的月历,认真观察图 1中的方框圈出五个数的关系,回答下列问题:
(1)请你用相同的方框在图 2中圈出五个数,使得五个数的和为 115;
(2)圈出的五个数的和能为 130吗?若能,在图中圈出,若不能,说明理由.
22 如图,从 A到 B时 0.5千米的上坡路,从 B到 C是 3千米的平路,从 C到 D是 2.5千米的上坡路,下坡
路速度都是每小时 6千米,平路上速度都是每小时 4千米,上坡路上速度都是每小时 3千米.如果小张和小
王分别从 A、D两地同时出发,相向步行,几小时两人相遇?
1617
23 有两个人玩“抢 10”的游戏,游戏规则如下:第一个人先说“1”或“1,2”;第二个人接着往下说一个或两个
数,然后轮到第一个人说一个或两个数都可以,但是不能连说三个数,谁先抢到 10,谁就胜.
(1)你认为这个游戏公平吗?说明你的理由.
(2)你有必胜的把握吗?说明你获胜的策略.
24 小明对北京市出租汽车的计费问题进行研究,他搜集了一些资料,部分信息如下:
收费项目 收费标准
3 公里以内收费 13 元
基本单价 2.3 元/公里
…… ……
备注:出租车计价段里程精确到 500米;出租汽车收费结算以元为单位,元以下四舍五入.
小明首先简化模型,从简单情形开始研究:
(1)只考虑白天正常行驶(无低速和等候);
(2)行驶路程 3公里以上时,计价器每 500米计价 1次,且每 1公里中前 500米计价 1.2元,后 500米计价
1.1元.
记一次运营出租车行驶的里程数为 x(单位:公里),相应的实付车费为 y(单位:元),小明想探究不同里程
数 x与实付车费 y之间的关系.小明进行了以下思考:
1 由上述信息可知,当行驶3公里以内时,都应付费 13元,若继续行驶,只要不超过 500米,计价器就不
会计价,仍只需付费 13元.即当 0<x<3.5时,y=13;
2 当行驶里程超过3.5公里但不超过 4公里时,计价器会在 13元的基础上新计价一次,即 13+1.2=14.2元,
四舍五入应付费 14元,即当 3.5≤x<4时,y=14;
3 以此类推……小明利用表格记录了 y随 x的变化情况,请你补全表格;
行驶里程数 x 0 0<x<3.5 3.5≤x<4 4≤x<4.5 4.5≤x<5 5≤x<5.5
实付车费y 0 13 14 15
若小明一次乘坐出租车付费25元,则出租车行驶路程的整数部分为 .
1718
25 老师给同学们出了下面这道题,把大家都给难住了,小明是学习委员,组织大家进行讨论.你也来参
与 吧.
图中长方形的面积是 180平方厘米,S1与 S2的面积都是 60平方厘米,阴影部分的面积是多少平方厘米?
小丽:“根据条件,可以知道四边形 DEBF的面积也是 60 1平方厘米,占长方形面积的 减去三角形 EBF的
3
面 积就是阴影部分的面积了.”
小林:“三角形 EBF是一个直角三角形,不知道 EB和 BF的长,怎么计算它的面积呢?”
小强:“如果知道它占长方形面积的几分之几也能求它的面积.”
小明:“大家的想法很好,如果知道 AE︰EB和 BF︰FC的比值,就可以求三角形 EBF是长方形面积的几
分 之几了.”
小明边画图边给大家解释:“例如 AE︰EB=2︰1,BF︰FC=2︰3,通过画图可以知道三角形 EBF占长方
形 面积的十五分之一.”
一直在沉思的李敏终于开口了:“如果在 DB之间画一条对角线,那么三角形 DBC的面积就是 90平方厘米,
它与三角形 DFC是等高的三角形,根据高相等,三角形的面积与底成…”
“我知道怎么求 BF与 FC的比了.”没等李敏说完,小明就高兴地叫了起来.
请你参考上面大家讨论的思路,求出阴影部分的面积.
26 数学中有很多有趣的题,图形分割就是其中一种,请你展开想象的翅膀,来对下列图形进行巧妙的分
割吧.
(1)请将一个等边三角形(图 1)分割成形状面积都相同的 3个部分.
(2)接下来请将图 2分割成形状面积都相同的 4个部分.(此图由 5个相同的正方形组成)
(3)请将图 3分割成形状面积相同的 8个部分.(此图由三个相同的正方形组成)
北京市-海淀区-101中学-分班考试卷答案
一、填空题
1
【答案】 丙>甲>乙
2
【答案】 70
3
【答案】 4
4
【答案】 ④
5
【答案】 415
6
【答案】 81
7
【答案】 戊
二、选择题
8
【答案】 A
9
【答案】 B
10
【答案】 D
11
【答案】 C
12
【答案】 D
13
【答案】 A
14
【答案】 C
15
【答案】 A
16
【答案】 B
17
【答案】 D
三、计算题
18
【答案】
(1)1002
(2)166680
四、解答题
19
【答案】
20
【答案】
(1)22km
(2)295L
21
【答案】
(1)
(2)不能
22
2
【答案】
3
23
【答案】
(1)不公平,先说者有主动权,按照 1、4、7、10这样的顺序就能获胜.
(2)有,先说 1,再说 4,然后说 7,最后抢到 10.
24
【答案】 ③5.5≤x<6;17;18;19
4 m
25
【答案】 50cm2
26
【答案】
一、填空题
1 1 1甲数的 与乙数的 相等,甲数的 25%与丙数的 20%相等.那么,甲、乙、丙的大小顺序是 .
5 4
2 1如图,将 10毫升酒装入一个圆锥形容器中,酒深正好占容器深的 .请问:再添入 毫升酒,可
2
装满此容器?
3 瓷器商店托快递公司送 800只瓷花瓶,双方约定每只运费是 3角 5分,若打破 1只,这只不但不给运费
还要赔偿 2元 5角钱.结果运到目的地后,快递公司共得运费 268.6元.在搬运过程中,打破了 只
花瓶.
4 将图甲围成图形乙的正方体,则在面①CDHE;②BCEF;③ABFG;④ADHG中,图甲中的“ 红心标
志所在的正方形是正方体中的面 .(填序号)
1011
5 小牛和爷爷、奶奶 8月 5日从北京出发,7日到 10日在南京旅游,8月 11日返回北京,北京与南京间的
火车和飞机票价如下:
交通工具 票价(元) 备注
飞机(普通舱) 1160 元 已满2周岁未满 l2周岁的儿童享受半价票
火车(硬卧) 290 元 身高1.1-1.4米的儿童享受半价票
他们在南京主要开支预算有以下几项:
住宿 伙食 市内交通 旅游景点门票
每日140元 每日90元 每日60元 每人 240元
小牛身高 1.38米,年龄 13周岁,他们准备了 6500元,去时乘坐火车,返回时乘坐飞机,照上面预计的开支,
他们大约还能剩余 元?
6 小明在一个正方形的棋盘里摆棋子,他先把最外层摆满,用了 40颗棋子,如果他要把整个棋盘摆满,还
需要 颗棋子.
7 甲、乙、丙、丁、戊五位同学在一次数学竞赛中得了前五名,发奖前老师要他们猜一猜各人所得的名次.
甲猜:乙第三名、丙第五名;
乙猜:戊第四名、丁第五名;
丙猜:甲第一名、戊第四名;
丁猜:丙第一名、乙第二名;
戊猜:甲第三名、丁第四名.
老师说:每个名次都有人猜对了,那么,获得第四名的是 .
二、选择题
8 5 5如果 a a,那么 a是( )
29 29
A.真分数 B.假分数 C.1 D.自然数
9 在圆中作一个最大的正方形,圆面积与正方形的面积之比是( )
A.2︰π B.π︰2 C.4︰3 D.4︰1
10 某班统计数学考试成绩,平均分是 84.2分,后来发现小明的成绩是 97分,而错误地统计为 79分,重新
计算后,平均成绩是 84.6分,则这个班的学生人数是( )
A.42 B.43 C.44 D.45
11 雷达二维平面定位的主要原理是:测量目标的两个信息——距离和角度,目标的表达方法为(y,a),其
中:y表示目标与探测器的距离;a表示以正东为始边,逆时针旋转的角度.如图,雷达探测器显示在点 A,
B,C处有目标出现,其中目标 A的位置表示为(5,30°),目标 B的位置表示为 B(4,150°).用这种方法
表示目标 C的位置,正确的是( )
A.(-3,300°) B.(3,60°)
C.(3,300°) D.(-3,60°)
12 已知一条直线 l和直线外的 A、B两点,以 A、B两点和直线上某一点做为三角形的三个顶点,就能画出
一个等腰三角形,如图中的等腰三角形 ABC.除此之外还能画出符合条件的等腰三角形个数是( )
A.1 B.2 C.3 D.4
13 在小红去培训班的路上,看到在一条公路上,每隔 100千米有一个仓库,共有五个仓库.A号仓库存有
10吨货物,B号仓库存有 20吨货物,E号仓库存有 40吨货物,其余两个仓是空的.现在想把所有的货物集
中存放在任意一个仓库里,如果每吨货物运输 1千米需要 1元运费,那么放在哪个仓库才能使运费最少?
( )
A.仓库 E B.仓库 D C.仓库 C D.仓库 B
12
14 近年来由于空气质量的变化,以及人们对自身健康的关注程度不断提高,空气净化器成为很多家庭的新
电器,某品牌的空气净化器厂家为进一步了解市场,制定生产计划.根据 2017下半年销售情况绘制了如下统
当 月 销 售 量
计图,其中同比增长率 1 100%.
去年同月销售量
下面有四个推断:
1 下半年各月销售量均比 2016同月销售量增多;
2 第四季度销售量占下半年销售量的七成以上;
3 下半年月均销售量为16万台;
4 下半年月销售量的中位数不超过10万台;
其中合理的是( )
A.①② B.①④ C.②③ D.③④
15 这群顽皮的小猴一共有( )只.
A.10 B.9 C.8 D.7
16 观察下面图形找规律.
正方形的个数 1 2 3 4 5 …
直角三角形的个数 0 4 8 …
按照上面的画法,如果要得到 100个直角三角形,需要画( )个正方形.
A.24 B.26 C.28 D.29
13
17 某游泳池长 25米,小林和小明两个人分别在游泳池的 A,B两边,同时朝着另一边游泳,他们游泳的时
间为 t(秒),其中 0≤t≤180,到 A边距离为 y(米),图中的实线和虚线分别表示小林和小明在游泳过程中 y
和 t的对应关系.下面有四个推断:
1 ①小明游泳的平均速度小于小林游泳的平均速度;
2 ②小明游泳的距离大于小林游泳的距离;
3 小明游75米时小林游了 90米;
4 小明与小林共相遇5次.
其中正确的是()
A.①② B.①③ C.③④ D.②④
三、计算题
18 计算
(2)(12345+23451+34512+45123+51234)+(1+2+3+4+5)
1415
四、解答题
19
(1)利用下面网格,画一个钝角三角形 ABC,其中 AB=AC,顶点 ABC都在格点上;
(2)画出三角形 ABC一条腰上的高;
(3)再找出两个格点 E、F使得三角形 EBC与三角形 ABC面积相等、形状相同,使得三角形 FBC与三角形
ABC面积相等、形状不同.
20 阅读所给材料,并解答问题.
正数和负数是表示两种具有相反意义的量.如:胜与负、收入与支出、零上温度与零下温度、海平面以上与
海平面以下、东与西、升与降等.这些都是具有相反意义的量,因此可以用正、负数来表示它们.例如:若
规定向东走 200米记作+200米,则向西走 300米记作-300米;反之,若规定向西走 300米记作+300米,
则向东走 200米记作-200.
根据上述材料,回答下列问题:
出租车司机小王某天下午的营运全是在东西走向的人民大道上行驶的.如果规定向东为正,向西为负,他这
天下午行车里程如下:(单位:千米)
+15 -3 +14 -11 +10 -12 -4 +15 +16 -18
(1)将最后一名乘客送到目的地时,小王距下午出车地点的距离是多少千米?
(2)若汽车耗油率为 2.5升/千米,则这天下午汽车共耗油多少升?
1516
21 下图为 2018年 1月的月历,认真观察图 1中的方框圈出五个数的关系,回答下列问题:
(1)请你用相同的方框在图 2中圈出五个数,使得五个数的和为 115;
(2)圈出的五个数的和能为 130吗?若能,在图中圈出,若不能,说明理由.
22 如图,从 A到 B时 0.5千米的上坡路,从 B到 C是 3千米的平路,从 C到 D是 2.5千米的上坡路,下坡
路速度都是每小时 6千米,平路上速度都是每小时 4千米,上坡路上速度都是每小时 3千米.如果小张和小
王分别从 A、D两地同时出发,相向步行,几小时两人相遇?
1617
23 有两个人玩“抢 10”的游戏,游戏规则如下:第一个人先说“1”或“1,2”;第二个人接着往下说一个或两个
数,然后轮到第一个人说一个或两个数都可以,但是不能连说三个数,谁先抢到 10,谁就胜.
(1)你认为这个游戏公平吗?说明你的理由.
(2)你有必胜的把握吗?说明你获胜的策略.
24 小明对北京市出租汽车的计费问题进行研究,他搜集了一些资料,部分信息如下:
收费项目 收费标准
3 公里以内收费 13 元
基本单价 2.3 元/公里
…… ……
备注:出租车计价段里程精确到 500米;出租汽车收费结算以元为单位,元以下四舍五入.
小明首先简化模型,从简单情形开始研究:
(1)只考虑白天正常行驶(无低速和等候);
(2)行驶路程 3公里以上时,计价器每 500米计价 1次,且每 1公里中前 500米计价 1.2元,后 500米计价
1.1元.
记一次运营出租车行驶的里程数为 x(单位:公里),相应的实付车费为 y(单位:元),小明想探究不同里程
数 x与实付车费 y之间的关系.小明进行了以下思考:
1 由上述信息可知,当行驶3公里以内时,都应付费 13元,若继续行驶,只要不超过 500米,计价器就不
会计价,仍只需付费 13元.即当 0<x<3.5时,y=13;
2 当行驶里程超过3.5公里但不超过 4公里时,计价器会在 13元的基础上新计价一次,即 13+1.2=14.2元,
四舍五入应付费 14元,即当 3.5≤x<4时,y=14;
3 以此类推……小明利用表格记录了 y随 x的变化情况,请你补全表格;
行驶里程数 x 0 0<x<3.5 3.5≤x<4 4≤x<4.5 4.5≤x<5 5≤x<5.5
实付车费y 0 13 14 15
若小明一次乘坐出租车付费25元,则出租车行驶路程的整数部分为 .
1718
25 老师给同学们出了下面这道题,把大家都给难住了,小明是学习委员,组织大家进行讨论.你也来参
与 吧.
图中长方形的面积是 180平方厘米,S1与 S2的面积都是 60平方厘米,阴影部分的面积是多少平方厘米?
小丽:“根据条件,可以知道四边形 DEBF的面积也是 60 1平方厘米,占长方形面积的 减去三角形 EBF的
3
面 积就是阴影部分的面积了.”
小林:“三角形 EBF是一个直角三角形,不知道 EB和 BF的长,怎么计算它的面积呢?”
小强:“如果知道它占长方形面积的几分之几也能求它的面积.”
小明:“大家的想法很好,如果知道 AE︰EB和 BF︰FC的比值,就可以求三角形 EBF是长方形面积的几
分 之几了.”
小明边画图边给大家解释:“例如 AE︰EB=2︰1,BF︰FC=2︰3,通过画图可以知道三角形 EBF占长方
形 面积的十五分之一.”
一直在沉思的李敏终于开口了:“如果在 DB之间画一条对角线,那么三角形 DBC的面积就是 90平方厘米,
它与三角形 DFC是等高的三角形,根据高相等,三角形的面积与底成…”
“我知道怎么求 BF与 FC的比了.”没等李敏说完,小明就高兴地叫了起来.
请你参考上面大家讨论的思路,求出阴影部分的面积.
26 数学中有很多有趣的题,图形分割就是其中一种,请你展开想象的翅膀,来对下列图形进行巧妙的分
割吧.
(1)请将一个等边三角形(图 1)分割成形状面积都相同的 3个部分.
(2)接下来请将图 2分割成形状面积都相同的 4个部分.(此图由 5个相同的正方形组成)
(3)请将图 3分割成形状面积相同的 8个部分.(此图由三个相同的正方形组成)
北京市-海淀区-101中学-分班考试卷答案
一、填空题
1
【答案】 丙>甲>乙
2
【答案】 70
3
【答案】 4
4
【答案】 ④
5
【答案】 415
6
【答案】 81
7
【答案】 戊
二、选择题
8
【答案】 A
9
【答案】 B
10
【答案】 D
11
【答案】 C
12
【答案】 D
13
【答案】 A
14
【答案】 C
15
【答案】 A
16
【答案】 B
17
【答案】 D
三、计算题
18
【答案】
(1)1002
(2)166680
四、解答题
19
【答案】
20
【答案】
(1)22km
(2)295L
21
【答案】
(1)
(2)不能
22
2
【答案】
3
23
【答案】
(1)不公平,先说者有主动权,按照 1、4、7、10这样的顺序就能获胜.
(2)有,先说 1,再说 4,然后说 7,最后抢到 10.
24
【答案】 ③5.5≤x<6;17;18;19
4 m
25
【答案】 50cm2
26
【答案】
同课章节目录
