湘教版数学七年级下册 复习课件:第三章《分解因式》(共23张PPT)
文档属性
| 名称 | 湘教版数学七年级下册 复习课件:第三章《分解因式》(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-02 21:29:34 | ||
图片预览






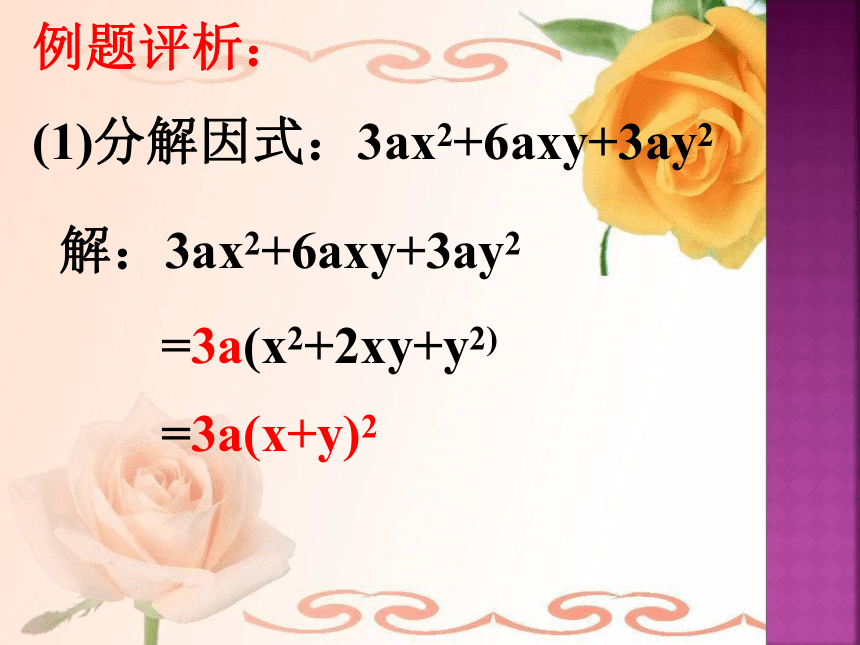

文档简介
课件23张PPT。因式分解复习因
式
分
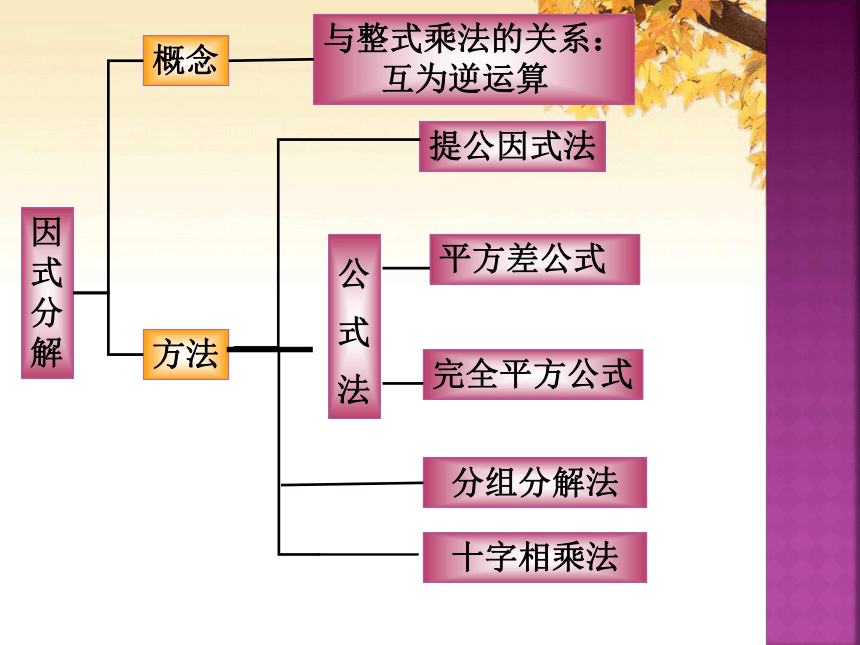
解概念方法与整式乘法的关系:
互为逆运算提公因式法公
式
法分组分解法平方差公式 完全平方公式十字相乘法口答:一、你还记得吗?1、把 化成 的形式,叫做把这个多项式因式分解。2、因式分解与 是互逆变形,分解的结果对不对可以用 运算检验。几个整式的乘积 整式乘法整式乘法一个多项式3、我们主要学习了因式分解的方法有: ((1)___________关键是找出各项的 ______提公因式法公因式。找公因式要注意以下四种变形关系:确定公因式的方法3、我们主要学习了因式分解的方法有:(2) ______________ 运用公式法平方差公式:
完全平方公式:二次三项式型:x2+(P+q)x+pq=(x+p)(x+q)检测1、下列有左到右的变形,属因式分解的是( )
(A)(a+2)(a-2)=a2-4
(B)a2-9=(a+3)(a-3)
(C)x2-1+2x=(x-1)(x+1)+2x
(D)x2+6x+10=(x+3)2+1 B2、已知x2-kx+25是一个完全平方式,
那么k的值为( )D3、已知多项式x2+mx-2n因式分解为(x+4)(x-3),则m=____,n=____.16A、5; B、-5 ;C、10 ; D、±10;例题评析:
(1)分解因式:3ax2+6axy+3ay2解:3ax2+6axy+3ay2=3a(x2+2xy+y2)=3a(x+y)2思考:要是这个多项式改为:
y2-x2+10x-25 (2)y2-(x2-10x+25)
=y2-(x-5)2
=[y+(x-5)][y-(x-5)]
=(y+x-5)(y-x+5)你还会分解吗?解:y2-(x2-10x+25)
归纳:因式分解的一般步骤:一提:如果多项式的各项有公因式,那么先提公因式;二套:如果多项式的各项没有公因式,那么可以尝试运用公式法来分解;
四检查。因式分解必须进行到每一个因式都不能再分解为止。三分组:如果多项式的各项没有公因式,也不能直接用公式,且项数超过三项,那么可以考虑分组来分解;注意: (1)如果多项式的第一项是“-”号,则先把“-”号提出来括号里各项要变号。 (2)如果多项式从整体上看既不能提公因式、也不能运用公式法,要将多项式化简整理,在选择合适的方法分解。 例如:分解因式:8 (x2-2y2)-x(7x+y)+xy将下列多项式因式分解因式分 解. (2) (x2+y2)2-4x2y2 (1)2a3-8a举一反三 你能行(4)(x3-x2)+(1-x)(3) -2x2+20x-50(5) (x+y)2+12(x+y)+36(6) a2-b2+2b-1 (1)2a3-8a解:原式=2a(a2-4)
= 2a(a+2) a-2)((2) (x2+y2)2-4x2y2解:原式=(x2+y2)2-(2xy)2
=(x2+y2+2xy)(x2+y2-2xy)
=(x+y)2(x-y)2(3) -2x2+20x-50解:原式=-(2x2-20x+50)
=-2(x2-10x+25)
=-2(x-5)2(4)(x3-x2)+(1-x)解:原式=x2(x-1)+(1-x)=x2(x-1)-(x-1)=(x-1)(x2-1)=(x-1)(x+1)(x-1)=(x-1)2(x+1)(5) (x+y)2+12(x+y)+36解:原式=(x+y)2+2·(x+y)·6+62=[(x+y)+6]2=(x+y+6)2(6) a2-b2+2b-1;
解:原式=a2-(b2-2b+1)
=a2-(b-1)2
=(a+b-1)(a-b+1)
因式分解应用: 求值、简便计算、变形。1、已知a+b=4,ab=-2,则a2b+ab2=——;
2、已知x+y=5,x2-y2=-20,则x-y=_____;
3、20062-62=__________;
112+66×13+392=___________-8-4402400025004、已知x+y=4,求0.5x2+xy+0.5y2的值。 解:0.5x2+xy+0.5y2
=0.5(x2+2xy+y2)
=0.5(x+y)2
=0.5×42
=81、已知(x+y)2-2x-2y+1=0,
求2x2+4xy+2y2的值。解:由题意:(x+y)2-2(x+y)+1=0
∴(x+y-1)2=0即x+y-1=0
∴x+y=1
∴2x2+4xy+2y2=2(x+y)2
=2×12=2拓展 2、已知 a=1000x+1001, b=1000x+1000, c=1000x+999, 求2a2+2b2+2c2-2ab-2bc-2ac的值。拓展
式
分
解概念方法与整式乘法的关系:
互为逆运算提公因式法公
式
法分组分解法平方差公式 完全平方公式十字相乘法口答:一、你还记得吗?1、把 化成 的形式,叫做把这个多项式因式分解。2、因式分解与 是互逆变形,分解的结果对不对可以用 运算检验。几个整式的乘积 整式乘法整式乘法一个多项式3、我们主要学习了因式分解的方法有: ((1)___________关键是找出各项的 ______提公因式法公因式。找公因式要注意以下四种变形关系:确定公因式的方法3、我们主要学习了因式分解的方法有:(2) ______________ 运用公式法平方差公式:
完全平方公式:二次三项式型:x2+(P+q)x+pq=(x+p)(x+q)检测1、下列有左到右的变形,属因式分解的是( )
(A)(a+2)(a-2)=a2-4
(B)a2-9=(a+3)(a-3)
(C)x2-1+2x=(x-1)(x+1)+2x
(D)x2+6x+10=(x+3)2+1 B2、已知x2-kx+25是一个完全平方式,
那么k的值为( )D3、已知多项式x2+mx-2n因式分解为(x+4)(x-3),则m=____,n=____.16A、5; B、-5 ;C、10 ; D、±10;例题评析:
(1)分解因式:3ax2+6axy+3ay2解:3ax2+6axy+3ay2=3a(x2+2xy+y2)=3a(x+y)2思考:要是这个多项式改为:
y2-x2+10x-25 (2)y2-(x2-10x+25)
=y2-(x-5)2
=[y+(x-5)][y-(x-5)]
=(y+x-5)(y-x+5)你还会分解吗?解:y2-(x2-10x+25)
归纳:因式分解的一般步骤:一提:如果多项式的各项有公因式,那么先提公因式;二套:如果多项式的各项没有公因式,那么可以尝试运用公式法来分解;
四检查。因式分解必须进行到每一个因式都不能再分解为止。三分组:如果多项式的各项没有公因式,也不能直接用公式,且项数超过三项,那么可以考虑分组来分解;注意: (1)如果多项式的第一项是“-”号,则先把“-”号提出来括号里各项要变号。 (2)如果多项式从整体上看既不能提公因式、也不能运用公式法,要将多项式化简整理,在选择合适的方法分解。 例如:分解因式:8 (x2-2y2)-x(7x+y)+xy将下列多项式因式分解因式分 解. (2) (x2+y2)2-4x2y2 (1)2a3-8a举一反三 你能行(4)(x3-x2)+(1-x)(3) -2x2+20x-50(5) (x+y)2+12(x+y)+36(6) a2-b2+2b-1 (1)2a3-8a解:原式=2a(a2-4)
= 2a(a+2) a-2)((2) (x2+y2)2-4x2y2解:原式=(x2+y2)2-(2xy)2
=(x2+y2+2xy)(x2+y2-2xy)
=(x+y)2(x-y)2(3) -2x2+20x-50解:原式=-(2x2-20x+50)
=-2(x2-10x+25)
=-2(x-5)2(4)(x3-x2)+(1-x)解:原式=x2(x-1)+(1-x)=x2(x-1)-(x-1)=(x-1)(x2-1)=(x-1)(x+1)(x-1)=(x-1)2(x+1)(5) (x+y)2+12(x+y)+36解:原式=(x+y)2+2·(x+y)·6+62=[(x+y)+6]2=(x+y+6)2(6) a2-b2+2b-1;
解:原式=a2-(b2-2b+1)
=a2-(b-1)2
=(a+b-1)(a-b+1)
因式分解应用: 求值、简便计算、变形。1、已知a+b=4,ab=-2,则a2b+ab2=——;
2、已知x+y=5,x2-y2=-20,则x-y=_____;
3、20062-62=__________;
112+66×13+392=___________-8-4402400025004、已知x+y=4,求0.5x2+xy+0.5y2的值。 解:0.5x2+xy+0.5y2
=0.5(x2+2xy+y2)
=0.5(x+y)2
=0.5×42
=81、已知(x+y)2-2x-2y+1=0,
求2x2+4xy+2y2的值。解:由题意:(x+y)2-2(x+y)+1=0
∴(x+y-1)2=0即x+y-1=0
∴x+y=1
∴2x2+4xy+2y2=2(x+y)2
=2×12=2拓展 2、已知 a=1000x+1001, b=1000x+1000, c=1000x+999, 求2a2+2b2+2c2-2ab-2bc-2ac的值。拓展
