18.1 勾股定理(2)
文档属性
| 名称 | 18.1 勾股定理(2) |  | |
| 格式 | rar | ||
| 文件大小 | 458.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-16 23:27:00 | ||
图片预览

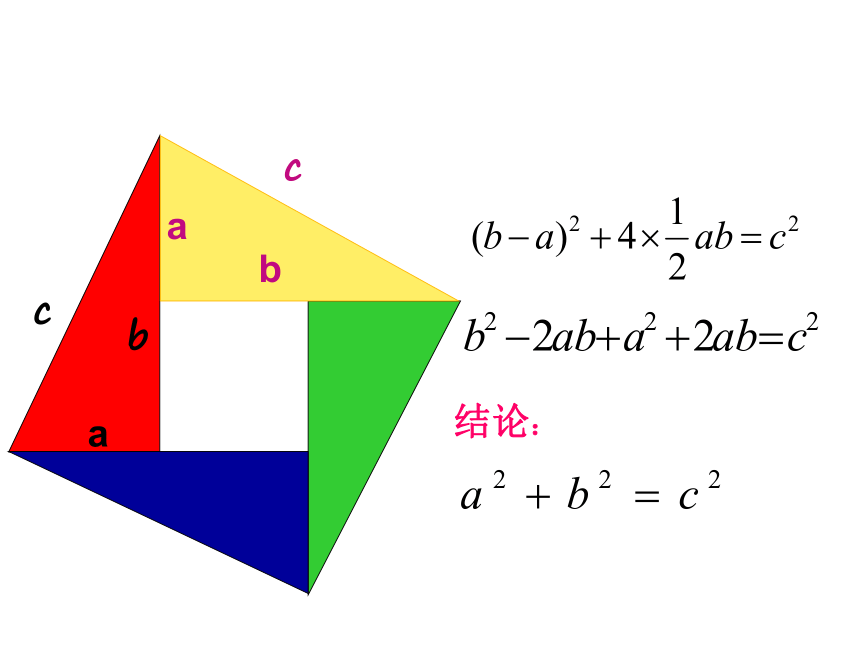
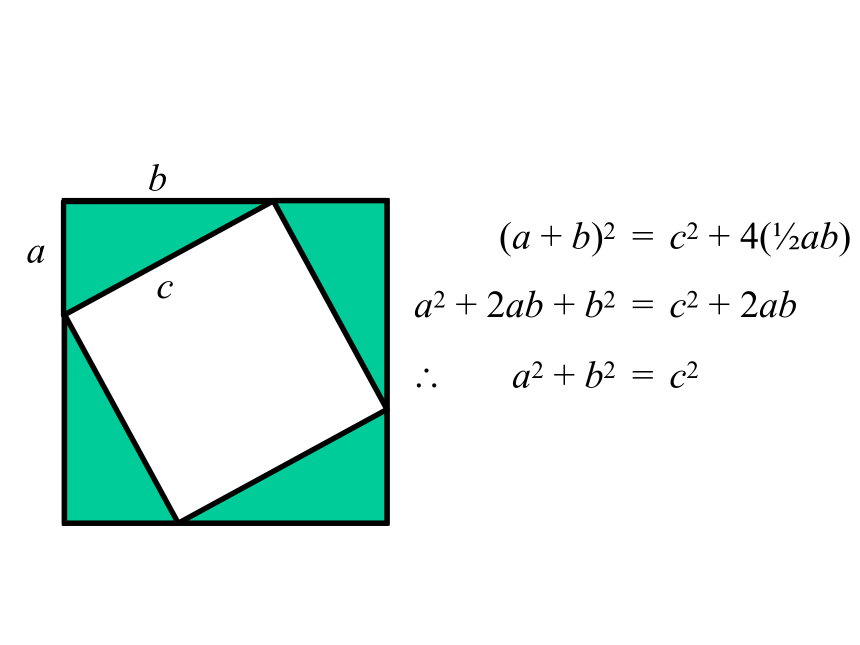

文档简介
(共16张PPT)
a
c
b
a
b
c
结论:
b
a
(a + b)2 = c2 + 4( ab)
a2 + 2ab + b2 = c2 + 2ab
a2 + b2 = c2
c
a
b
c
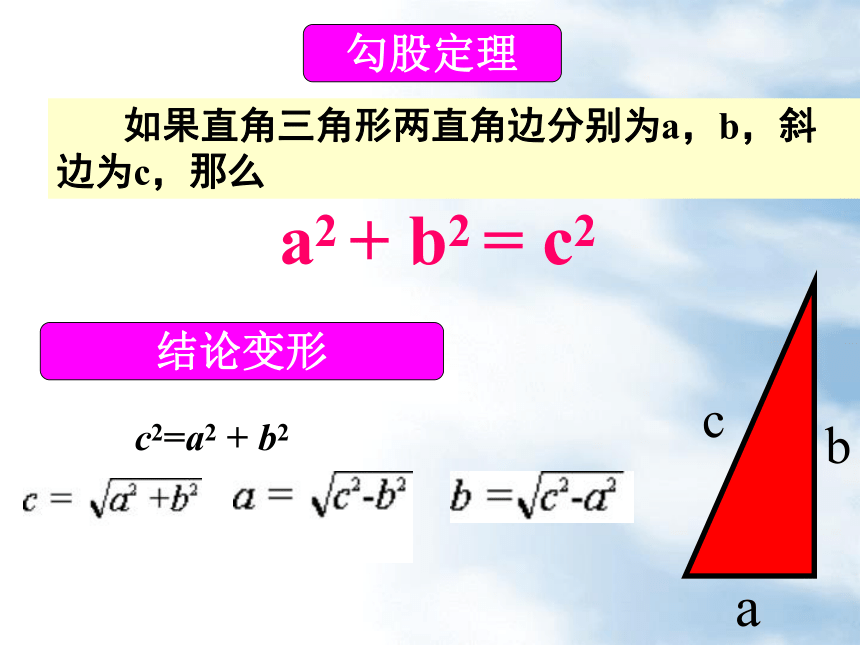
c2=a2 + b2
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
结论变形
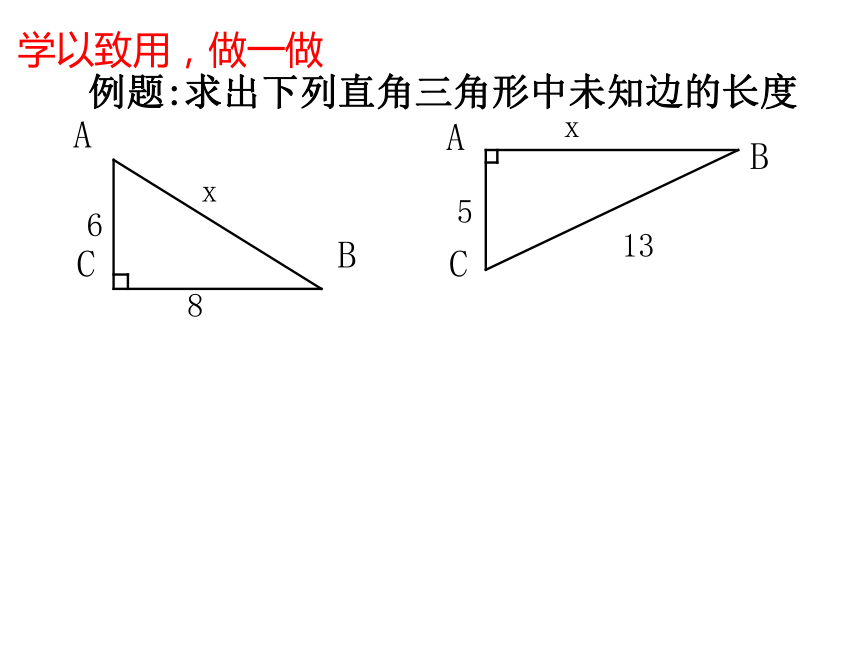
例题:求出下列直角三角形中未知边的长度
6
8
x
5
x
13
学以致用,做一做
A
C
B
A
C
B
1.在Rt△ABC中, ∠C=90°,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b;
总结:已知直角三角形的任意两边,通过勾股定理可以求出第三边.
(4)若a:b=1:2,c=6
则a,b各多长
(5)若∠A=300,a=3,则b ,c各多长
⑴已知: a=3, b=4,求c
⑵已知: c =10,a=6,求b
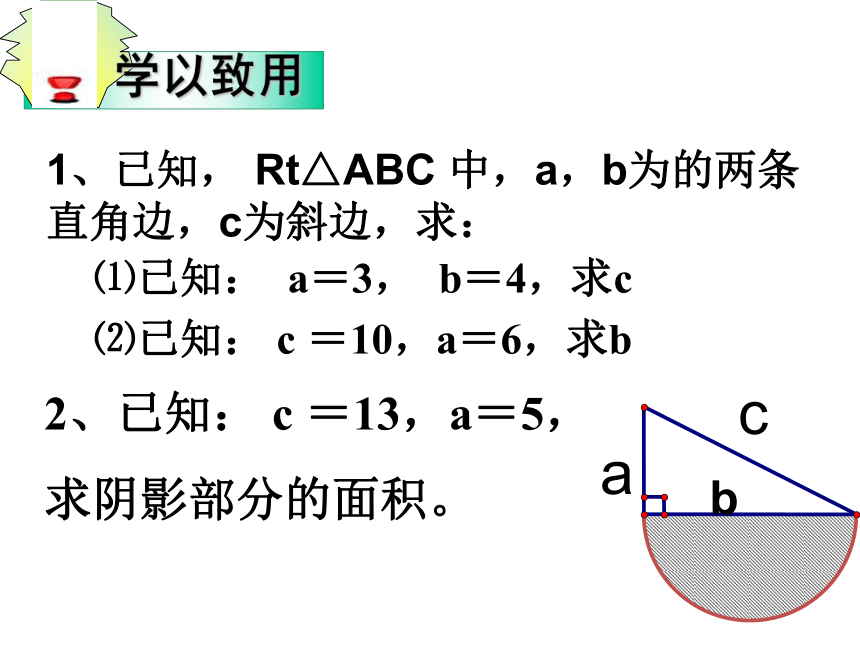
学以致用
1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
2、已知: c =13,a=5,
求阴影部分的面积。
a
c
b
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
y=0
学以致用,做一做
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
做一做:
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和
思考
S1
S2
解:∵ SE= 49
S1=SA+SB
S2=SC+SD
∴ SA+SB+SC+SD
= S1+S2 = SE = 49
1
1
美丽的勾股树
1.在△ABC中, ∠C=90°,a=6,b=8,
则c=____
2.在△ABC中, a=6,b=8,试求第三边c的值
10
y=0
练一练
3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________
10
y=0
练一练
或
活学活用
探究1
一个门框尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
1m
2m
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和, 等于斜边c平方。
a2+b2 =c2
⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。
a
c
b
a
b
c
结论:
b
a
(a + b)2 = c2 + 4( ab)
a2 + 2ab + b2 = c2 + 2ab
a2 + b2 = c2
c
a
b
c
c2=a2 + b2
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
结论变形
例题:求出下列直角三角形中未知边的长度
6
8
x
5
x
13
学以致用,做一做
A
C
B
A
C
B
1.在Rt△ABC中, ∠C=90°,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b;
总结:已知直角三角形的任意两边,通过勾股定理可以求出第三边.
(4)若a:b=1:2,c=6
则a,b各多长
(5)若∠A=300,a=3,则b ,c各多长
⑴已知: a=3, b=4,求c
⑵已知: c =10,a=6,求b
学以致用
1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
2、已知: c =13,a=5,
求阴影部分的面积。
a
c
b
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
y=0
学以致用,做一做
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
做一做:
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和
思考
S1
S2
解:∵ SE= 49
S1=SA+SB
S2=SC+SD
∴ SA+SB+SC+SD
= S1+S2 = SE = 49
1
1
美丽的勾股树
1.在△ABC中, ∠C=90°,a=6,b=8,
则c=____
2.在△ABC中, a=6,b=8,试求第三边c的值
10
y=0
练一练
3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________
10
y=0
练一练
或
活学活用
探究1
一个门框尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
1m
2m
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和, 等于斜边c平方。
a2+b2 =c2
⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长。
