7.2 万有引力定律 课件(共19张PPT)
文档属性
| 名称 | 7.2 万有引力定律 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-24 07:45:25 | ||
图片预览





文档简介
(共19张PPT)
7.2 万有引力定律
第七章 万有引力与宇宙航行
人教版(2019)必修 第二册
1. 知道万有引力存在于任意两个物体之间,知道其表达式和适用范围。
2.理解万有引力定律的推导过程,认识在科学规律发现过程中大胆猜想与严格求证的重要性.
3.知道万有引力定律的发现使地球上的重物下落与天体运动完成了人类认识上的统一。
4.会应用万有引力定律解决简单的引力计算问题。
知道万有引力定律公式中r的物理意义,了解引力常量G的测定在科学史上的重要意义。
学习目标
各行星都围绕着太阳运行,说明太阳与行星之间的引力是使行星如此运动的主要原因。引力的大小和方向能确定吗?
导入新课
为什么行星绕太阳做满足开普勒定律的运动?
1.假设与猜想
⑴行星受到太阳引力
⑵F引大小与r有关
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
胡克的贡献
F引∝
新课入
一、行星与太阳之间的引力
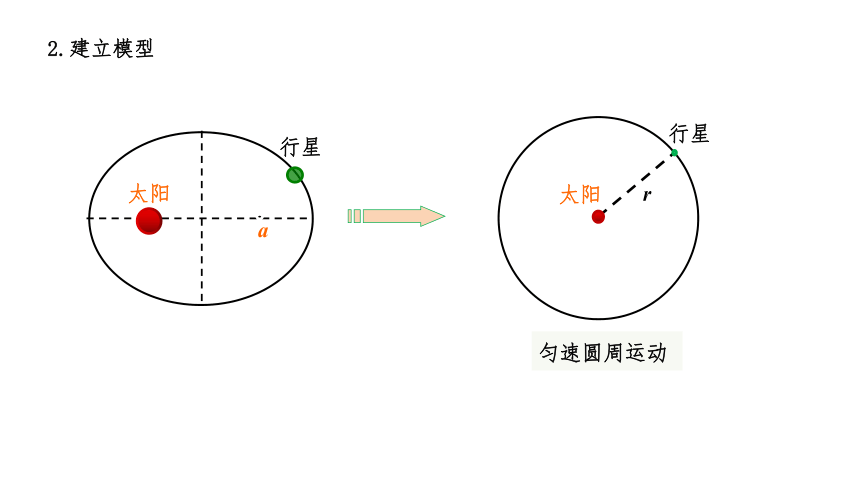
2.建立模型
太阳
行星
a
匀速圆周运动
太阳
行星
r
太阳
行星
r
M
m
设行星的质量为 m,速度为 v,行星与太阳间的距离为 r,太阳的质量为M。
3.推理与演绎
⑴太阳对行星的引力
学生自行推导
核心:开普勒第三定律
结论:
⑵行星对太阳的引力
①受力物体:
太阳
②类比⑴
结论:
写成等式
⑶太阳与行星之间的引力
由牛顿第三定律,得
F=F′
综合归纳:
行星围绕太阳运转
月球围绕地球运转
熟透的苹果落向地球
问题及验证目的
月球—地球
地球—地面附近物体
相互作用与太阳——行星间的引力性质是否相同?
二、月——地检验
月球
苹果
假设
地球与月球间的作用力
地球与苹果间的作用力
是同一种力
太阳与行星间的作用力
推导
猜想
事实
符合
√
当时已知的一些量:
地表重力加速度:g = 9.8 m/s2
地球半径:R = 6400×103 m
月亮周期:T=27.3天≈ 2.36×106 s
月亮轨道半径:r ≈ 60R
验证
是否宇宙中任意两个物体之间都有这样的力呢
把以上结论推广到宇宙中的一切物体之间。
结论:地面物体受地球的引力、月球所受地球的引力,与太阳、行星间的引力一样,都遵循相同的规律。
思考:
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量的乘积成正比、与它们之间距离的二次方成反比。
2.表达式:
G是引力常量
①两个质点之间
②质量分布均匀的球体之间
r为两个球心之间的距离。
m1
m2
r
两物体间距远大于物体的线度
3.公式适用条件:
新课入
三、万有引力定律
两物体的距离 r 的物理含义?
思考:
计算:两个质量均为10 kg,相距为1 m,的密度均匀的铁球之间的万有引力有多大呢?请计算两个铁球之间的万有引力引力,该引力值与单个铁球受到的重力之比是多少?
4.发现万有引力定律的重要意义:
为什么我们平时感受不到与周围物体的引力呢?
思考:
揭示了地面上物体运动的规律和天体上物体的运动遵从同一规律,让人们认识到天体上物体的运动规律也是可以认识的,解放了人们的思想,给人们探索自然的奥秘建立了极大信心, 对后来的物理学、天文学的发展具有深远的影响。
比例系数G,叫做引力常量,适用于任何两个物体。
1.单位:
2.大小:
3.引力常量G的测定:
卡文迪许扭秤实验
①证明了万有引力的存在;
②使得万有引力定律有了真正的实用价值,可测定远离地球的一些天体的质量、平均密度等。
4.测定引力常量的意义
放大思想
新课入
四、引力常量
1.对于万有引力定律的表述式,下列说法中正确的是 ( )
A.公式中G为引力常量,它是由实验测得的,而不是人为规定的
B.当r趋近于零时,万有引力趋于无穷大
C.m1与m2受到的引力大小总是相等的,方向相反,是一对平衡力
D.m1与m2受到的引力大小总足相等的,而与m1、m2是否相等无关
AD
2.在宇宙中存在一些远离其他恒星的、由质量相等的三颗行星组成的三星体统,已知其中一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆轨道运行,假设每个星体的质量均为m,引力常量为G,星体的间距为a,忽略其他星体对三星系统的作用力,求解每颗行星所受万有引力的合力?
A
B
C
FC
FB
F合
解:行星A受到C和B的万有引力FB、FC,根据万有引力定律得:
故万有引力的合力沿∠CAB的角平分线,利用力的合成可知:
3.如图所示,一个质量为 M 的匀质实心球,半径为 R。从球内挖去一个直径为 R 的小球,放在距离为 d 的地方,求两者之间的引力。
处理方法:
割补法处理不规则物体产生万有引力问题:
本质:
将不规则物体对空间中某质点的引力,视为填充后的规则物体和填充部分各自对质点引力的差值。
是通过填和补,使得原来残缺物体变成规则情形。
填补完整后的实心球对小球的引力:
剩余部分对右侧小球的引力为:
填补的小球对右侧小球的引力为:
【解析】
万有引力定律
行星与太阳的引力
月—地检验
万有引力定律
猜想
验证
结论
内容
表达式
引力常量
适用条件
课堂小结:
新课入
课堂小结
7.2 万有引力定律
第七章 万有引力与宇宙航行
人教版(2019)必修 第二册
1. 知道万有引力存在于任意两个物体之间,知道其表达式和适用范围。
2.理解万有引力定律的推导过程,认识在科学规律发现过程中大胆猜想与严格求证的重要性.
3.知道万有引力定律的发现使地球上的重物下落与天体运动完成了人类认识上的统一。
4.会应用万有引力定律解决简单的引力计算问题。
知道万有引力定律公式中r的物理意义,了解引力常量G的测定在科学史上的重要意义。
学习目标
各行星都围绕着太阳运行,说明太阳与行星之间的引力是使行星如此运动的主要原因。引力的大小和方向能确定吗?
导入新课
为什么行星绕太阳做满足开普勒定律的运动?
1.假设与猜想
⑴行星受到太阳引力
⑵F引大小与r有关
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
胡克的贡献
F引∝
新课入
一、行星与太阳之间的引力
2.建立模型
太阳
行星
a
匀速圆周运动
太阳
行星
r
太阳
行星
r
M
m
设行星的质量为 m,速度为 v,行星与太阳间的距离为 r,太阳的质量为M。
3.推理与演绎
⑴太阳对行星的引力
学生自行推导
核心:开普勒第三定律
结论:
⑵行星对太阳的引力
①受力物体:
太阳
②类比⑴
结论:
写成等式
⑶太阳与行星之间的引力
由牛顿第三定律,得
F=F′
综合归纳:
行星围绕太阳运转
月球围绕地球运转
熟透的苹果落向地球
问题及验证目的
月球—地球
地球—地面附近物体
相互作用与太阳——行星间的引力性质是否相同?
二、月——地检验
月球
苹果
假设
地球与月球间的作用力
地球与苹果间的作用力
是同一种力
太阳与行星间的作用力
推导
猜想
事实
符合
√
当时已知的一些量:
地表重力加速度:g = 9.8 m/s2
地球半径:R = 6400×103 m
月亮周期:T=27.3天≈ 2.36×106 s
月亮轨道半径:r ≈ 60R
验证
是否宇宙中任意两个物体之间都有这样的力呢
把以上结论推广到宇宙中的一切物体之间。
结论:地面物体受地球的引力、月球所受地球的引力,与太阳、行星间的引力一样,都遵循相同的规律。
思考:
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量的乘积成正比、与它们之间距离的二次方成反比。
2.表达式:
G是引力常量
①两个质点之间
②质量分布均匀的球体之间
r为两个球心之间的距离。
m1
m2
r
两物体间距远大于物体的线度
3.公式适用条件:
新课入
三、万有引力定律
两物体的距离 r 的物理含义?
思考:
计算:两个质量均为10 kg,相距为1 m,的密度均匀的铁球之间的万有引力有多大呢?请计算两个铁球之间的万有引力引力,该引力值与单个铁球受到的重力之比是多少?
4.发现万有引力定律的重要意义:
为什么我们平时感受不到与周围物体的引力呢?
思考:
揭示了地面上物体运动的规律和天体上物体的运动遵从同一规律,让人们认识到天体上物体的运动规律也是可以认识的,解放了人们的思想,给人们探索自然的奥秘建立了极大信心, 对后来的物理学、天文学的发展具有深远的影响。
比例系数G,叫做引力常量,适用于任何两个物体。
1.单位:
2.大小:
3.引力常量G的测定:
卡文迪许扭秤实验
①证明了万有引力的存在;
②使得万有引力定律有了真正的实用价值,可测定远离地球的一些天体的质量、平均密度等。
4.测定引力常量的意义
放大思想
新课入
四、引力常量
1.对于万有引力定律的表述式,下列说法中正确的是 ( )
A.公式中G为引力常量,它是由实验测得的,而不是人为规定的
B.当r趋近于零时,万有引力趋于无穷大
C.m1与m2受到的引力大小总是相等的,方向相反,是一对平衡力
D.m1与m2受到的引力大小总足相等的,而与m1、m2是否相等无关
AD
2.在宇宙中存在一些远离其他恒星的、由质量相等的三颗行星组成的三星体统,已知其中一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆轨道运行,假设每个星体的质量均为m,引力常量为G,星体的间距为a,忽略其他星体对三星系统的作用力,求解每颗行星所受万有引力的合力?
A
B
C
FC
FB
F合
解:行星A受到C和B的万有引力FB、FC,根据万有引力定律得:
故万有引力的合力沿∠CAB的角平分线,利用力的合成可知:
3.如图所示,一个质量为 M 的匀质实心球,半径为 R。从球内挖去一个直径为 R 的小球,放在距离为 d 的地方,求两者之间的引力。
处理方法:
割补法处理不规则物体产生万有引力问题:
本质:
将不规则物体对空间中某质点的引力,视为填充后的规则物体和填充部分各自对质点引力的差值。
是通过填和补,使得原来残缺物体变成规则情形。
填补完整后的实心球对小球的引力:
剩余部分对右侧小球的引力为:
填补的小球对右侧小球的引力为:
【解析】
万有引力定律
行星与太阳的引力
月—地检验
万有引力定律
猜想
验证
结论
内容
表达式
引力常量
适用条件
课堂小结:
新课入
课堂小结
