人教版高中物理选择性必修一1.5弹性碰撞和非弹性碰撞 课件(共23张PPT)
文档属性
| 名称 | 人教版高中物理选择性必修一1.5弹性碰撞和非弹性碰撞 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-24 07:55:33 | ||
图片预览







文档简介
(共23张PPT)
1.5 弹性碰撞和非弹性碰撞
人教版选择性必修第一册
掌握简谐运动振幅的物理意义。
课堂引入
生活中存在着各种碰撞现象
打台球
打乒乓球
钉钉子
打桩机打桩
碰撞是自然界中常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……
物体碰撞时系统的动量守恒。那么,在各种碰撞中能量又是如何变化的?
作用时间短
相互作用力大
位移小
碰撞
一个钢球碰撞另一个静止的钢球,如果两个钢球质量相等,碰撞后第一个钢球静止,第二个钢球可以摆起相同的高度,说明碰撞过程中没有能量损失,碰撞过程中能量守恒。
此类碰撞过程中:动量守恒、
机械能守恒。
如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另
一个以速度v向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞前后该系统的总动能是否会相等?
碰撞过程中动量守恒
碰前动能:
碰后动能:
碰撞过程中:动量守恒、机械能不守恒。
>
碰撞后两物体粘在一起(或者具有共同速度)的碰撞叫完全非弹性碰撞。
动量守恒,机械能损失最大。
1、弹性碰撞:
如果系统在碰撞前后机械能不变,这类碰撞叫作弹性碰撞。
动量守恒,机械能守恒。
一、弹性碰撞和非弹性碰撞
如果系统在碰撞后机械能减少,这类碰撞叫作非弹性碰撞。
动量守恒,机械能不守恒。
2、非弹性碰撞:
3、完全非弹性碰撞:
如何列式表达?
二、弹性碰撞的实例分析
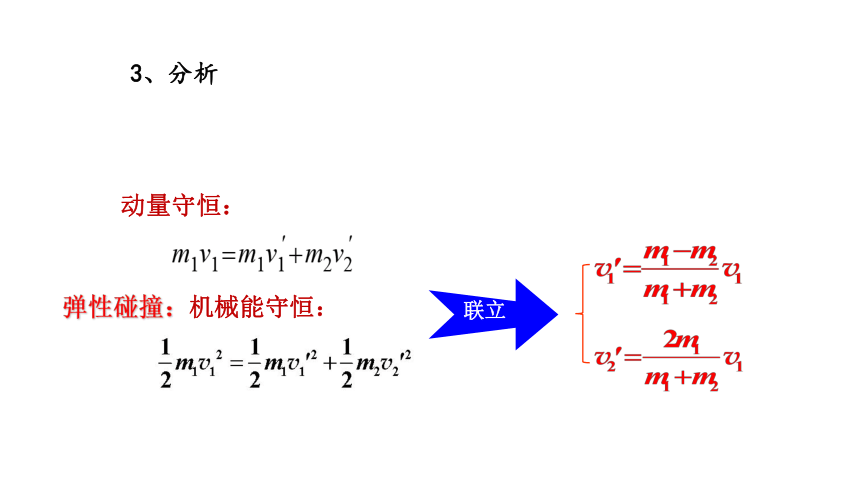
动量守恒:
弹性碰撞:机械能守恒:
联立
3、分析
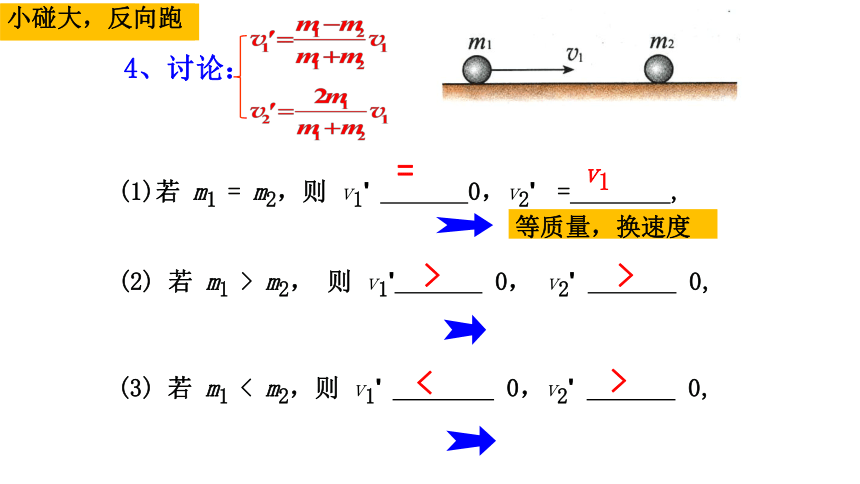
若 m1 = m2,则 v1 0,v2 = ,
(2) 若 m1 > m2, 则 v1 0, v2 0,
(3) 若 m1 < m2,则 v1 0,v2 0,
等质量,换速度
大碰小,同向跑
小碰大,反向跑
=
v1
>
>
<
>
4、讨论:
(5) 若 m1>>m2 ,则v1 ≈ ,v2 ≈ ,
极小碰极大,大不变,小等速反弹
极大碰极小,大不变,小加倍
(4)若m1<v1
2v1
-v1
0
被动球获得速度最大
被动球的动能
若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A 和 B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v1/ 和 v2/ 分别是多大?
思考、讨论
将A和B看作系统:
碰撞过程中系统动量守恒
弹性碰撞中没有机械能损失
若v2=0时,结论与前面的相同!
非弹性碰撞:动量守恒,机械能损失
完全非弹性碰撞:动量守恒,机械能损失最大
①动量制约(系统动量守恒的原则):即碰撞过程必须受到“动量守恒定律的制约”
②动能制约:即在碰撞过程,碰撞双方的总动能不会增加
③运动制约:即碰撞过程还将受到运动的合理性要求的制约(碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理。)
守恒
不增
合理
三、“碰撞过程”的制约
1、两球A、B在光滑水平面上沿同一直线,同一方向运动,mA=2kg,mB=3kg,vA=6m/s,vB=2m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )
A. vA’= 4.5m/s vB’= 3m/s
B. vA’= 3m/s vB’= 4m/s
C. vA’= -1.5m/s vB’= 7m/s
D. vA’= 7.5m/s vB’= 1m/s
B
课堂练习
2、光滑水平轨道上有三个木块A、B、C,质量分别为mA=mB=m,mC=2m,开始时B、C均静止,A以初速度v0向右运动,A与B发生弹性正碰后,B又与C发生碰撞并粘在一起,求:
(1)B与C 碰撞前后B的速度分别是多大?
(2)B与C 碰撞中损失的动能是多少?
课堂练习
3、在气垫导轨上,一个质量为400g的滑块一15cm/s的速度与另一质量为200g、速度为10cm/s并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。(结果保留两位有效数字)求:
课堂练习
(1)碰撞后滑块速度的大小和方向?
(2)在这次碰撞中,两滑块共损失多少机械能?
课堂小结
动量守恒,机械能损失最大。
1、弹性碰撞:
动量守恒,机械能守恒。
一、弹性碰撞和非弹性碰撞
动量守恒,机械能不守恒。
2、非弹性碰撞:
3、完全非弹性碰撞:
二、弹性碰撞的实例分析
1、等质量,换速度
2、大碰小,同向跑
3、小碰大,反向跑
4、极小碰极大,大不变,小等速反弹
5、极大碰极小,大不变,小加倍
三、“碰撞过程”的制约
①动量守恒
②动能不增
③运动合理
知识拓展
3、
谢 谢 指 导
1.5 弹性碰撞和非弹性碰撞
人教版选择性必修第一册
掌握简谐运动振幅的物理意义。
课堂引入
生活中存在着各种碰撞现象
打台球
打乒乓球
钉钉子
打桩机打桩
碰撞是自然界中常见的现象。陨石撞击地球而对地表产生破坏,网球受球拍撞击而改变运动状态……
物体碰撞时系统的动量守恒。那么,在各种碰撞中能量又是如何变化的?
作用时间短
相互作用力大
位移小
碰撞
一个钢球碰撞另一个静止的钢球,如果两个钢球质量相等,碰撞后第一个钢球静止,第二个钢球可以摆起相同的高度,说明碰撞过程中没有能量损失,碰撞过程中能量守恒。
此类碰撞过程中:动量守恒、
机械能守恒。
如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另
一个以速度v向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞前后该系统的总动能是否会相等?
碰撞过程中动量守恒
碰前动能:
碰后动能:
碰撞过程中:动量守恒、机械能不守恒。
>
碰撞后两物体粘在一起(或者具有共同速度)的碰撞叫完全非弹性碰撞。
动量守恒,机械能损失最大。
1、弹性碰撞:
如果系统在碰撞前后机械能不变,这类碰撞叫作弹性碰撞。
动量守恒,机械能守恒。
一、弹性碰撞和非弹性碰撞
如果系统在碰撞后机械能减少,这类碰撞叫作非弹性碰撞。
动量守恒,机械能不守恒。
2、非弹性碰撞:
3、完全非弹性碰撞:
如何列式表达?
二、弹性碰撞的实例分析
动量守恒:
弹性碰撞:机械能守恒:
联立
3、分析
若 m1 = m2,则 v1 0,v2 = ,
(2) 若 m1 > m2, 则 v1 0, v2 0,
(3) 若 m1 < m2,则 v1 0,v2 0,
等质量,换速度
大碰小,同向跑
小碰大,反向跑
=
v1
>
>
<
>
4、讨论:
(5) 若 m1>>m2 ,则v1 ≈ ,v2 ≈ ,
极小碰极大,大不变,小等速反弹
极大碰极小,大不变,小加倍
(4)若m1<
2v1
-v1
0
被动球获得速度最大
被动球的动能
若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A 和 B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v1/ 和 v2/ 分别是多大?
思考、讨论
将A和B看作系统:
碰撞过程中系统动量守恒
弹性碰撞中没有机械能损失
若v2=0时,结论与前面的相同!
非弹性碰撞:动量守恒,机械能损失
完全非弹性碰撞:动量守恒,机械能损失最大
①动量制约(系统动量守恒的原则):即碰撞过程必须受到“动量守恒定律的制约”
②动能制约:即在碰撞过程,碰撞双方的总动能不会增加
③运动制约:即碰撞过程还将受到运动的合理性要求的制约(碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理。)
守恒
不增
合理
三、“碰撞过程”的制约
1、两球A、B在光滑水平面上沿同一直线,同一方向运动,mA=2kg,mB=3kg,vA=6m/s,vB=2m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )
A. vA’= 4.5m/s vB’= 3m/s
B. vA’= 3m/s vB’= 4m/s
C. vA’= -1.5m/s vB’= 7m/s
D. vA’= 7.5m/s vB’= 1m/s
B
课堂练习
2、光滑水平轨道上有三个木块A、B、C,质量分别为mA=mB=m,mC=2m,开始时B、C均静止,A以初速度v0向右运动,A与B发生弹性正碰后,B又与C发生碰撞并粘在一起,求:
(1)B与C 碰撞前后B的速度分别是多大?
(2)B与C 碰撞中损失的动能是多少?
课堂练习
3、在气垫导轨上,一个质量为400g的滑块一15cm/s的速度与另一质量为200g、速度为10cm/s并沿相反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。(结果保留两位有效数字)求:
课堂练习
(1)碰撞后滑块速度的大小和方向?
(2)在这次碰撞中,两滑块共损失多少机械能?
课堂小结
动量守恒,机械能损失最大。
1、弹性碰撞:
动量守恒,机械能守恒。
一、弹性碰撞和非弹性碰撞
动量守恒,机械能不守恒。
2、非弹性碰撞:
3、完全非弹性碰撞:
二、弹性碰撞的实例分析
1、等质量,换速度
2、大碰小,同向跑
3、小碰大,反向跑
4、极小碰极大,大不变,小等速反弹
5、极大碰极小,大不变,小加倍
三、“碰撞过程”的制约
①动量守恒
②动能不增
③运动合理
知识拓展
3、
谢 谢 指 导
