北京市第十五中学2024-2025学年九年级上学期开学考数学试题(图片版,无答案)
文档属性
| 名称 | 北京市第十五中学2024-2025学年九年级上学期开学考数学试题(图片版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 804.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 00:00:00 | ||
图片预览


文档简介
2024北京十五中初三(上)开学考
数 学
时间:60分钟
一、选择题(每题 2分,共 20分)
1. 要使二次根式 x 3 有意义,x的值可以是( )
A. 4 B. 2 C. 1 D. 0
2. 下列计算中,正确的是( )
2
2
A. ( 2 ) = 2 B. ( 2) = 2 C. 6 3 = 2 D. 8 2 = 4
3. 已知 x = 5 1时,则代数式 x2 + 2x + 3的值( )
A. 1 B. 4 C. 7 D. 3
4. 平面直角坐标系内,点 P (1, 3 )到原点的距离是( )
A. 2 B. 2 C. 3 +1 D. 4
5. 若菱形的两条对角线的长分别为 6 和 10,则菱形的面积为( )
A. 60 B. 30 C. 14 D. 15
6. 《九章算术》内容丰富,与实际生活联系紧密,在书上讲述了这样一个问题“今有垣高一丈.倚木于
垣,上与垣齐、引木却行一尺、其木至地.问木长几何?”其内容可以表述为:“有一面墙,高 1 丈.将
一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向
远离墙的方向移动 1 尺,则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺?”(说明:1 丈=10 尺)
设木杆长 x尺,依题意,下列方程正确的是( )
x2 = (x 1)2 2A. +1 B. (x +1)
2 = x2 +102
2 2 2
C. x = (x 1) +10 D. (x +1)
2 = x2 +12
7. 想要计算一组数据:197,202,200,201,199,198,203 的方差 s2,在计算平均数的过程中,将这组
数据的每一个数都减去 200,得到一组新数据﹣3,2,0,1,﹣1,﹣2,3,且新的这组数据的方差为 4,
则 s2为( )
A. 4 B. 16 C. 196 D. 204
8. 正十二边形的外角和为( )
A. 30 B. 150 C. 360 D. 1800
9. 已知O 为数轴原点,如图,
(1)在数轴上截取线段OA = 2;
(2)过点A 作直线n垂直于OA;
(3)在直线n上截取线段 AB = 3;
(4)以O 为圆心,OB 的长为半径作弧,交数轴于点C .
第1页/共24页
根据以上作图过程及所作图形,有如下四个结论:①OC = 5;②OB = 13 ;③3 OC 4 ;④
AC =1.上述结论中,所有正确结论的序号是( )
A. ①② B. ①③ C. ②③ D. ②④
10. 如图,点 A、B、C 在同一条线上,点 B 在点 A,C 之间,点 D,E 在直线 AC 同侧, AB BC ,
A = C = 90 ,△EAB≌△BCD ,连接 DE,设 AB a , BC = b , DE = c ,给出下面三个结论:
① a + b c ;②a +b a2 +b2 ;③ 2 (a + b) c ;
上述结论中,所有正确结论的序号是( )
A. ①② B. ①③ C. ②③ D. ①②③
二、填空题(每题 3分,共 30分)
11. 计算:已知 x = 5 + 3 , y = 5 3 ,则 xy = __________.
12. 下列命题:①两直线平行,同位角相等;②对顶角相等;③平行四边形的对角线互相平分.其中逆命题
是真命题的命题共有_____个.
13. 如图所示的正方形网格中,每一个小正方形的面积均为1,正方形 ABCM ,CDEN ,MNPQ的顶点
都在格点上,则正方形MNPQ的面积为__________.
第2页/共24页
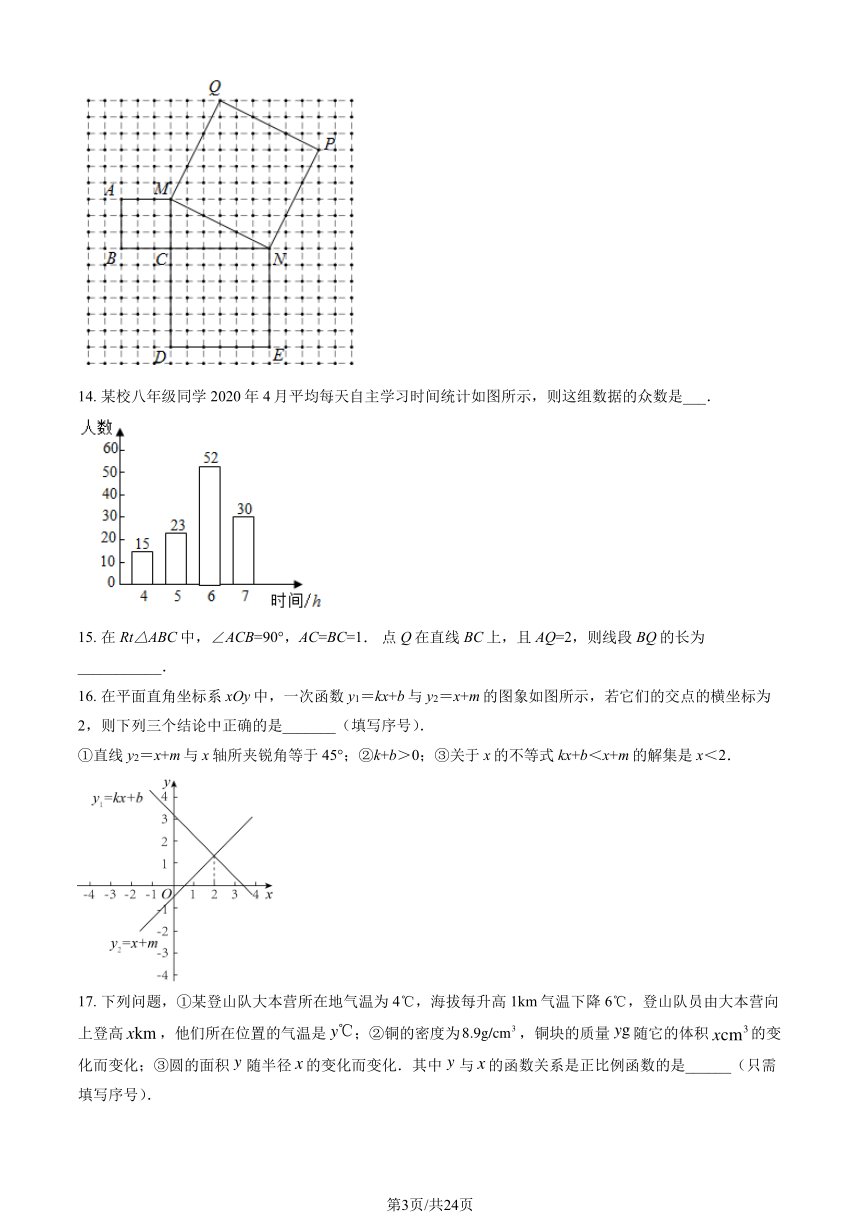
14. 某校八年级同学 2020 年 4 月平均每天自主学习时间统计如图所示,则这组数据的众数是___.
15. 在 Rt△ABC中,∠ACB=90°,AC=BC=1. 点 Q在直线 BC上,且 AQ=2,则线段 BQ的长为
___________.
16. 在平面直角坐标系 xOy中,一次函数 y1=kx+b与 y2=x+m的图象如图所示,若它们的交点的横坐标为
2,则下列三个结论中正确的是_______(填写序号).
①直线 y2=x+m与 x轴所夹锐角等于 45°;②k+b>0;③关于 x的不等式 kx+b<x+m的解集是 x<2.
17. 下列问题,①某登山队大本营所在地气温为 4℃,海拔每升高 1km 气温下降 6℃,登山队员由大本营向
上登高 xkm ,他们所在位置的气温是 y℃;②铜的密度为8.9g/cm3 ,铜块的质量 yg 随它的体积 xcm3的变
化而变化;③圆的面积 y 随半径 x的变化而变化.其中 y 与 x的函数关系是正比例函数的是______(只需
填写序号).
第3页/共24页
18. 为了践行“首都市民卫生健康公约”,某班级举办“七步洗手法”比赛活动,小明的单项成绩如表所
示(各项成绩均按百分制计):
项目 书面测试 实际操作 宣传展示
成绩(分) 96 98 96
若按书面测试占 30%、实际操作占 50%、宣传展示占 20%,计算参赛个人的综合成绩(百分制),则小明
的最后得分是________.
19. 在平面直角坐标系 xOy中,若直线 y=2x+3 向下平移 n个单位长度后,与直线 y=﹣x+2 的交点在第
一象限,则 n的取值范围是________.
20. 如图 1,在矩形 ABCD中,动点 P从点 B出发,沿 B →C → D → A的路径匀速运动到点 A处停
止.设点 P运动路程为 x, PAB 的面积为 y,表示 y与 x的函数关系的图象如图 2 所示;则下列结论:①
a = 4;②b = 20 ;③当 x = 9 时,点 P运动到点 D处;④当 y = 9时,点 P在线段 BC 或 DA上,其中所
有正确结论的序号的是________.
三、解答题(共 50分,21~26每题 6分,27-28每题 7分)
21. 计算
3
(1) 12 10 5 + 8
2
(2)已知 x = 3 1,求代数式 x2 + 2x的值.
22. 如图,平行四边形 ABCD的对角线 AC , 相交于点 O,E、F分别是OA、OC 的中点.求证:
BE = DF .
23. 已知:如图,在 ABC 中, AB = AC .
求作:以 AC 为对角线的矩形 ADCE .
作法:①以点 A 为圆心,适当长为半径画弧,分别交 AB,AC 于点 M,N;分别以点 M,N为圆心,大于
1
MN 的长为半径作弧,两弧在 BAC 的内部相交于点 P,作射线 AP 与 BC 交于点 D;
2
第4页/共24页
②以点 A 为圆心,CD的长为半径画弧;再以点 C 为圆心, AD 的长为半径画弧,两弧在 AC 的右侧交于
点 E;
③连接 AE,CE .
四边形 ADCE 为所求的矩形.
(1)根据以上作法,使用直尺和圆规补全图形(保留作图痕迹);
(2)完成以下证明.
证明:∵ AE = CD,CE = AD,
∴四边形 ADCE 为平行四边形( ).(填推理的依据)
由作图可知, AD 平分 BAC ,
又∵ AB = AC ,
∴ AD ⊥ BC ( ).(填推理的依据)
∴ ADC = 90 .
∴平行四边形 ADCE 是矩形( ).(填推理的依据)
24. 在平面直角坐标系 xOy 中,一次函数 y = kx + b 的图象经过点 ( 1,0), (1,2).
(1)求这个一次函数的解析式;
(2)当 x 3时,对于 x的每一个值,函数: y = mx 1(m 0)的值小于函数 y = kx + b 的值,直接写
出m 的取值范围.
25. 某校舞蹈队共有 12 名学生,测量并获取了所有学生的身高(单位:cm),数据整理如下:
a.12 名学生的身高∶
160,164,164,165,166,167,167,167,168,168,169,171,
b.12 名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
166.3 m n
(1)写出表中m ,n的值;
(2)现将 12 名学生分成如下甲乙两组.对于不同组的学生,如果一组学生的身高的方差越小,则认为该
组舞台呈现效果越好.据此推断:在下列两组学生中,舞台呈现效果更好的是 (填“甲组”或“乙
组”);
第5页/共24页
甲组学生的身高 165 167 167 168 168 171
乙组学生的身高 160 164 164 166 167 169
(3)该舞蹈队要选六名学生参加艺术节比赛,已经确定甲组四名参赛的学生的身高分别为 165,167,
168,168.在乙组选择另外两名参赛学生时,要求所选的两名学生与已确定的四名学生所组成的参赛队身
高的方差最小,则乙组选出的另外两名学生的身高分别为 和 .
26. 如图,矩形 ABCD中,点 E为边 AB 上任意一点,连结CE ,点 F为线段CE 的中点,过点 F作
MN ⊥ CE ,MN 与 AB 、CD分别相交于点 M、N,连结CM 、 EN .
(1)求证:四边形CNEM 为菱形;
(2)若 AB =10, AD = 4,当 AE = 2时,求EM 的长.
27. 如图,正方形 ABCD中,点M 在 BC 延长线上,点 P 是 BM 的中点,连接 AP ,在射线 BC 上方作
PQ ⊥ AP ,且 PQ = AP.连接MD,MQ.
(1)补全图形;
(2)用等式表示MD 与MQ 的数量关系并证明;
(3)连接CQ,若正方形边长为 5,CQ = 6 2 直接写出线段CM 的长.
28. 在平面直角坐标系 xOy 中,对于线段 AB 和点 Q,给出如下定义:若在直线 y = x 上存在点 P,使得四
边形 ABPQ 为平行四边形,则称点 Q为线段 AB 的“相随点”.
第6页/共24页
(1)已知,点 A(1,3), B (5,3).
①在点Q1 (1,5),Q2 ( 1,3),Q3 (0, 4),Q4 ( 5,0)中,线段 AB 的“相随点”是 ;
②若点 Q为线段 AB 的“相随点”,连接OQ , BQ,直接写出OQ + BQ的最小值及此时点 Q的坐标;
(2)已知点 A( 2,3),点 B (2, 1),正方形CDEF 边长为 2,且以点 (t,1)为中心,各边与坐标轴垂直或
平行,若对于正方形CDEF 上的任意一点,都存在线段 AB 上的两点 M,N,使得该点为线段MN 的“相
随点”,请直接写出 t 的取值范围.
第7页/共24页
数 学
时间:60分钟
一、选择题(每题 2分,共 20分)
1. 要使二次根式 x 3 有意义,x的值可以是( )
A. 4 B. 2 C. 1 D. 0
2. 下列计算中,正确的是( )
2
2
A. ( 2 ) = 2 B. ( 2) = 2 C. 6 3 = 2 D. 8 2 = 4
3. 已知 x = 5 1时,则代数式 x2 + 2x + 3的值( )
A. 1 B. 4 C. 7 D. 3
4. 平面直角坐标系内,点 P (1, 3 )到原点的距离是( )
A. 2 B. 2 C. 3 +1 D. 4
5. 若菱形的两条对角线的长分别为 6 和 10,则菱形的面积为( )
A. 60 B. 30 C. 14 D. 15
6. 《九章算术》内容丰富,与实际生活联系紧密,在书上讲述了这样一个问题“今有垣高一丈.倚木于
垣,上与垣齐、引木却行一尺、其木至地.问木长几何?”其内容可以表述为:“有一面墙,高 1 丈.将
一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向
远离墙的方向移动 1 尺,则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺?”(说明:1 丈=10 尺)
设木杆长 x尺,依题意,下列方程正确的是( )
x2 = (x 1)2 2A. +1 B. (x +1)
2 = x2 +102
2 2 2
C. x = (x 1) +10 D. (x +1)
2 = x2 +12
7. 想要计算一组数据:197,202,200,201,199,198,203 的方差 s2,在计算平均数的过程中,将这组
数据的每一个数都减去 200,得到一组新数据﹣3,2,0,1,﹣1,﹣2,3,且新的这组数据的方差为 4,
则 s2为( )
A. 4 B. 16 C. 196 D. 204
8. 正十二边形的外角和为( )
A. 30 B. 150 C. 360 D. 1800
9. 已知O 为数轴原点,如图,
(1)在数轴上截取线段OA = 2;
(2)过点A 作直线n垂直于OA;
(3)在直线n上截取线段 AB = 3;
(4)以O 为圆心,OB 的长为半径作弧,交数轴于点C .
第1页/共24页
根据以上作图过程及所作图形,有如下四个结论:①OC = 5;②OB = 13 ;③3 OC 4 ;④
AC =1.上述结论中,所有正确结论的序号是( )
A. ①② B. ①③ C. ②③ D. ②④
10. 如图,点 A、B、C 在同一条线上,点 B 在点 A,C 之间,点 D,E 在直线 AC 同侧, AB BC ,
A = C = 90 ,△EAB≌△BCD ,连接 DE,设 AB a , BC = b , DE = c ,给出下面三个结论:
① a + b c ;②a +b a2 +b2 ;③ 2 (a + b) c ;
上述结论中,所有正确结论的序号是( )
A. ①② B. ①③ C. ②③ D. ①②③
二、填空题(每题 3分,共 30分)
11. 计算:已知 x = 5 + 3 , y = 5 3 ,则 xy = __________.
12. 下列命题:①两直线平行,同位角相等;②对顶角相等;③平行四边形的对角线互相平分.其中逆命题
是真命题的命题共有_____个.
13. 如图所示的正方形网格中,每一个小正方形的面积均为1,正方形 ABCM ,CDEN ,MNPQ的顶点
都在格点上,则正方形MNPQ的面积为__________.
第2页/共24页
14. 某校八年级同学 2020 年 4 月平均每天自主学习时间统计如图所示,则这组数据的众数是___.
15. 在 Rt△ABC中,∠ACB=90°,AC=BC=1. 点 Q在直线 BC上,且 AQ=2,则线段 BQ的长为
___________.
16. 在平面直角坐标系 xOy中,一次函数 y1=kx+b与 y2=x+m的图象如图所示,若它们的交点的横坐标为
2,则下列三个结论中正确的是_______(填写序号).
①直线 y2=x+m与 x轴所夹锐角等于 45°;②k+b>0;③关于 x的不等式 kx+b<x+m的解集是 x<2.
17. 下列问题,①某登山队大本营所在地气温为 4℃,海拔每升高 1km 气温下降 6℃,登山队员由大本营向
上登高 xkm ,他们所在位置的气温是 y℃;②铜的密度为8.9g/cm3 ,铜块的质量 yg 随它的体积 xcm3的变
化而变化;③圆的面积 y 随半径 x的变化而变化.其中 y 与 x的函数关系是正比例函数的是______(只需
填写序号).
第3页/共24页
18. 为了践行“首都市民卫生健康公约”,某班级举办“七步洗手法”比赛活动,小明的单项成绩如表所
示(各项成绩均按百分制计):
项目 书面测试 实际操作 宣传展示
成绩(分) 96 98 96
若按书面测试占 30%、实际操作占 50%、宣传展示占 20%,计算参赛个人的综合成绩(百分制),则小明
的最后得分是________.
19. 在平面直角坐标系 xOy中,若直线 y=2x+3 向下平移 n个单位长度后,与直线 y=﹣x+2 的交点在第
一象限,则 n的取值范围是________.
20. 如图 1,在矩形 ABCD中,动点 P从点 B出发,沿 B →C → D → A的路径匀速运动到点 A处停
止.设点 P运动路程为 x, PAB 的面积为 y,表示 y与 x的函数关系的图象如图 2 所示;则下列结论:①
a = 4;②b = 20 ;③当 x = 9 时,点 P运动到点 D处;④当 y = 9时,点 P在线段 BC 或 DA上,其中所
有正确结论的序号的是________.
三、解答题(共 50分,21~26每题 6分,27-28每题 7分)
21. 计算
3
(1) 12 10 5 + 8
2
(2)已知 x = 3 1,求代数式 x2 + 2x的值.
22. 如图,平行四边形 ABCD的对角线 AC , 相交于点 O,E、F分别是OA、OC 的中点.求证:
BE = DF .
23. 已知:如图,在 ABC 中, AB = AC .
求作:以 AC 为对角线的矩形 ADCE .
作法:①以点 A 为圆心,适当长为半径画弧,分别交 AB,AC 于点 M,N;分别以点 M,N为圆心,大于
1
MN 的长为半径作弧,两弧在 BAC 的内部相交于点 P,作射线 AP 与 BC 交于点 D;
2
第4页/共24页
②以点 A 为圆心,CD的长为半径画弧;再以点 C 为圆心, AD 的长为半径画弧,两弧在 AC 的右侧交于
点 E;
③连接 AE,CE .
四边形 ADCE 为所求的矩形.
(1)根据以上作法,使用直尺和圆规补全图形(保留作图痕迹);
(2)完成以下证明.
证明:∵ AE = CD,CE = AD,
∴四边形 ADCE 为平行四边形( ).(填推理的依据)
由作图可知, AD 平分 BAC ,
又∵ AB = AC ,
∴ AD ⊥ BC ( ).(填推理的依据)
∴ ADC = 90 .
∴平行四边形 ADCE 是矩形( ).(填推理的依据)
24. 在平面直角坐标系 xOy 中,一次函数 y = kx + b 的图象经过点 ( 1,0), (1,2).
(1)求这个一次函数的解析式;
(2)当 x 3时,对于 x的每一个值,函数: y = mx 1(m 0)的值小于函数 y = kx + b 的值,直接写
出m 的取值范围.
25. 某校舞蹈队共有 12 名学生,测量并获取了所有学生的身高(单位:cm),数据整理如下:
a.12 名学生的身高∶
160,164,164,165,166,167,167,167,168,168,169,171,
b.12 名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
166.3 m n
(1)写出表中m ,n的值;
(2)现将 12 名学生分成如下甲乙两组.对于不同组的学生,如果一组学生的身高的方差越小,则认为该
组舞台呈现效果越好.据此推断:在下列两组学生中,舞台呈现效果更好的是 (填“甲组”或“乙
组”);
第5页/共24页
甲组学生的身高 165 167 167 168 168 171
乙组学生的身高 160 164 164 166 167 169
(3)该舞蹈队要选六名学生参加艺术节比赛,已经确定甲组四名参赛的学生的身高分别为 165,167,
168,168.在乙组选择另外两名参赛学生时,要求所选的两名学生与已确定的四名学生所组成的参赛队身
高的方差最小,则乙组选出的另外两名学生的身高分别为 和 .
26. 如图,矩形 ABCD中,点 E为边 AB 上任意一点,连结CE ,点 F为线段CE 的中点,过点 F作
MN ⊥ CE ,MN 与 AB 、CD分别相交于点 M、N,连结CM 、 EN .
(1)求证:四边形CNEM 为菱形;
(2)若 AB =10, AD = 4,当 AE = 2时,求EM 的长.
27. 如图,正方形 ABCD中,点M 在 BC 延长线上,点 P 是 BM 的中点,连接 AP ,在射线 BC 上方作
PQ ⊥ AP ,且 PQ = AP.连接MD,MQ.
(1)补全图形;
(2)用等式表示MD 与MQ 的数量关系并证明;
(3)连接CQ,若正方形边长为 5,CQ = 6 2 直接写出线段CM 的长.
28. 在平面直角坐标系 xOy 中,对于线段 AB 和点 Q,给出如下定义:若在直线 y = x 上存在点 P,使得四
边形 ABPQ 为平行四边形,则称点 Q为线段 AB 的“相随点”.
第6页/共24页
(1)已知,点 A(1,3), B (5,3).
①在点Q1 (1,5),Q2 ( 1,3),Q3 (0, 4),Q4 ( 5,0)中,线段 AB 的“相随点”是 ;
②若点 Q为线段 AB 的“相随点”,连接OQ , BQ,直接写出OQ + BQ的最小值及此时点 Q的坐标;
(2)已知点 A( 2,3),点 B (2, 1),正方形CDEF 边长为 2,且以点 (t,1)为中心,各边与坐标轴垂直或
平行,若对于正方形CDEF 上的任意一点,都存在线段 AB 上的两点 M,N,使得该点为线段MN 的“相
随点”,请直接写出 t 的取值范围.
第7页/共24页
同课章节目录
