人教版2024-2025学年八年级数学上册基础强化11.2.1三角形的内角同步练习(含解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册基础强化11.2.1三角形的内角同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-25 00:00:00 | ||
图片预览



文档简介
人教版2024-2025学年八年级数学上册基础强化
11.2.1 三角形的内角同步练习
班级: 姓名:
同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你收获满满,学习进步,榜上有名!
一、单选题
1.如图,,被直线所截,且,平分,过点G作,若,则的度数为( )
A. B. C. D.
2.已知一个三角形三个内角度数的比是1:2:3,则其最大内角的度数为( )
A. B. C. D.
3.如图摆放的一副直角三角尺,,,与相交于点,当时,的度数是( )
A. B. C. D.
4.一个三角形的三个内角的度数比是,最大的角是( )
A. B. C.
5.如图,已知在中,,现将分别沿边翻折得到,则的度数为( )
A. B. C. D.
6.将一块三角板和一把直尺如图放置,若,则的度数为( )
A. B. C. D.
7.如图,已知点是射线上一点,过作交射线于点,交射线于点,下列结论正确的是( )
A.的余角只有 B.图中互余的角共有对
C.的补角只有 D.图中与互补的角共有个
8.如商,在△ABC中,∠A=α,∠ABC与∠ACD的平分钱交十点A1,得∠A1,∠A1BC与∠A1CD的平分线相交于点A2,得∠A2,……∠A6BC与∠A6CD的平分线相交于点A7,得∠A7,则∠A7=( )
A. B. C. D.
9.如图①,将一副三角板中的两个直角叠放在一起,其中,,,,现按住三角板不动,将三角板绕点C顺时针旋转,图②是旋转过程中的某一位置,当B、C、E三点第一次共线时旋转停止,记(k为常数),给出下列四个说法:
①当时,直线与直线相交所成的锐角度数为;
②当时,;
③当时,;
④当时,.其中正确的说法的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
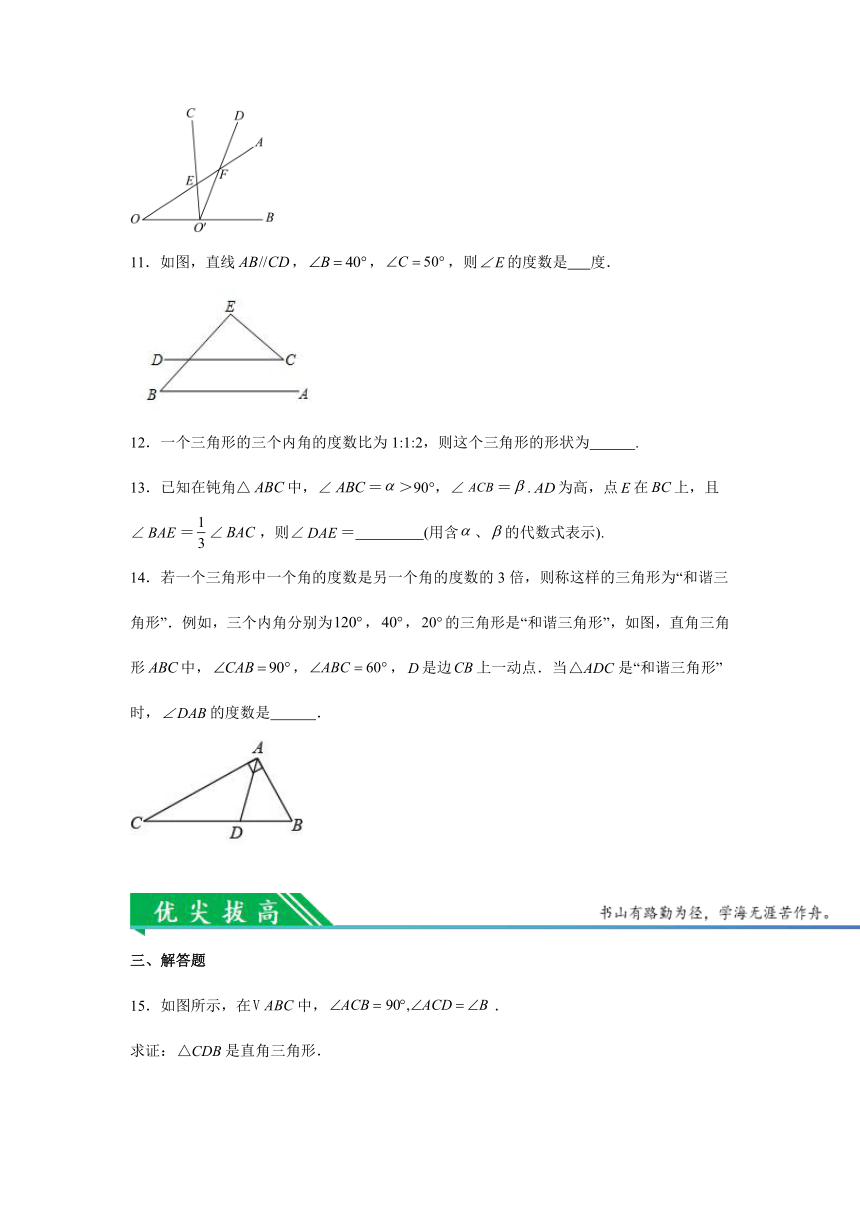
10.如图,的顶点落在的边上,边,分别交的边于点E,F.若,,则的度数是
11.如图,直线,,,则的度数是 度.
12.一个三角形的三个内角的度数比为1:1:2,则这个三角形的形状为 .
13.已知在钝角△中,∠=>90°,∠=.为高,点在上,且∠=∠,则∠= (用含、的代数式表示).
14.若一个三角形中一个角的度数是另一个角的度数的3倍,则称这样的三角形为“和谐三角形”.例如,三个内角分别为,,的三角形是“和谐三角形”,如图,直角三角形中,,,是边上一动点.当是“和谐三角形”时,的度数是 .
三、解答题
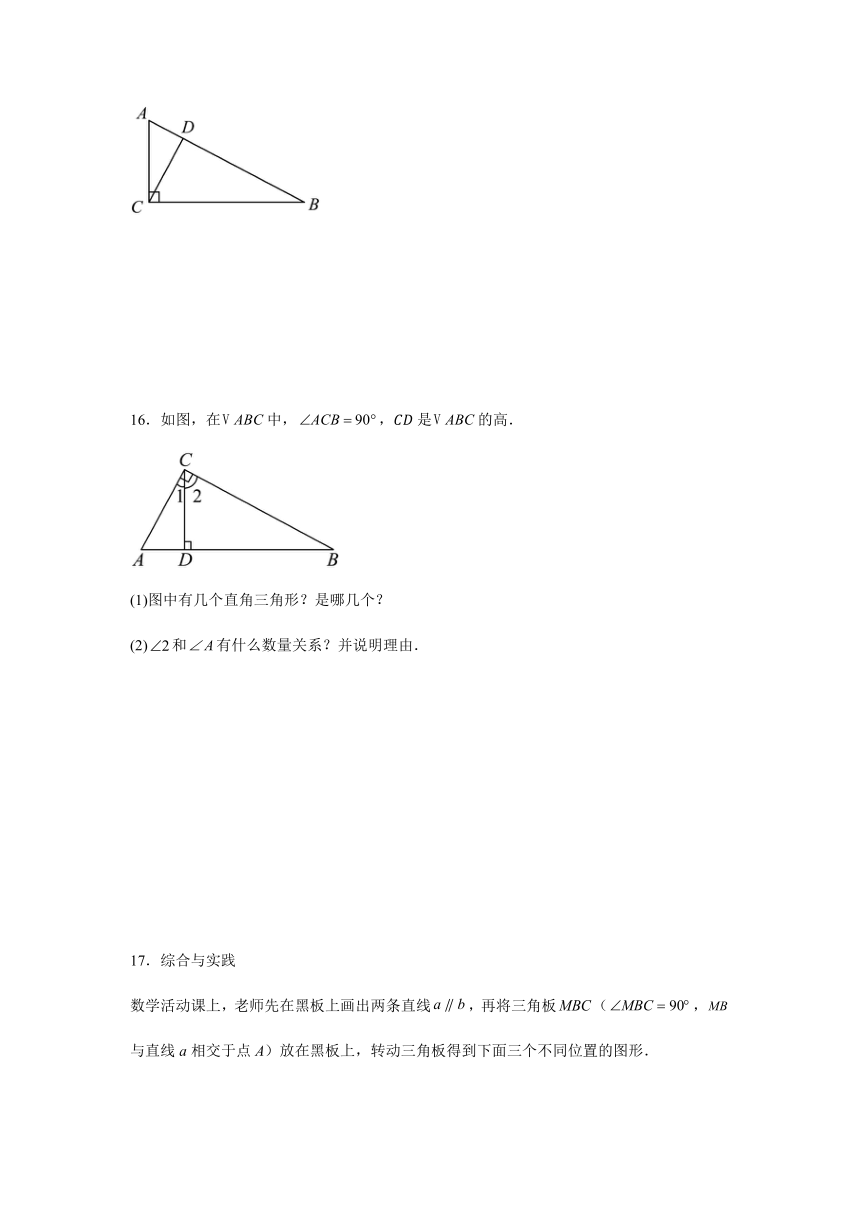
15.如图所示,在中,.
求证:是直角三角形.
16.如图,在中,,是的高.
(1)图中有几个直角三角形?是哪几个?
(2)和有什么数量关系?并说明理由.
17.综合与实践
数学活动课上,老师先在黑板上画出两条直线,再将三角板(,与直线a相交于点A)放在黑板上,转动三角板得到下面三个不同位置的图形.
(1)【初步探究】
如图①,若点B在直线b上,,则________°;
(2)【深入探究】
如图②,若点B在直线a,b之间,与有怎样的数量关系?写出结论,并给出证明;
(3)【拓展延伸】
如图③,若点B在直线b的下方,请直接写出与之间的数量关系.
18.如图,点,分别是的边,上任意一点,将沿折叠至,已知.
(1)若已知,探究,,之间的关系.
(2)若已知,探究,,之间的关系(直接写出结论,不需要证明).
(3)若已知,探究,,之间的关系(直接写出结论,不需要证明).
19.在△ABC中,∠B=20°+∠A,∠C=∠B-10°,求∠A的度数.
20.如图 1,一张△ABC 纸片,点 M、N 分别是 AC、BC 上两点.
(1)若沿直线 MN 折叠,使 C 点落在 BN 上,则∠AMC′与∠ACB 的数量关系是 ;
(2)若折成图 2 的形状.猜想∠AMC′、∠BNC′和∠ACB 的数量关系,并说明理由.
猜想: .
理由:
(3)若折成图3 的形状,猜想∠AMC′、∠BNC′和∠ACB 的数量关系是 .(写出结论即可).
(4)将上述问题推广,如图4,将四边形 ABCD 纸片沿 MN 折叠,使点 C、D 落在四边形 ABNM 的内部时,∠AMD′+∠BNC′与∠C、∠D 之间的数量关系 是 (写出结论即可).
1.B
【分析】本题考查了平行线的性质,三角形的内角和定理以及角平分线的性质,正确熟练运用知识点进行角度计算是解答本题的关键.
先在中通过三角形内角和定理得出度数,再由平行线的性质求出的度数,最后由角平分线的性质即可求出答案.
【详解】解:∵,,
∴,
∵,
∴,
∴,
∵平分,
∴.
故选:B.
2.C
【分析】已知三角形三个内角的度数之比,可以设三个内角度数为:,,,根据三角形的内角和等于,列方程求三个内角的度数,确定最大的内角的度数.
【详解】解:设三个内角度数为:,,,
根据三角形内角和定理,可知,
解得:.
∴,即最大的内角是90°.
故选:C.
【点睛】本题考查了三角形内角和定理,解题的关键是见比设参.
3.B
【分析】本题主要考查了平行线的性质和三角形内角和定理.过点作,则有,,又因为和都是特殊直角三角形,,,可以得到,,进而可求解的度数,再根据平角的定义即可得出答案.
【详解】解:过点作,
∵,
∴,
,,
在和中,,,
,,
,,
,
,
,
故选:B.
4.B
【分析】此题考查了三角形内角和定理,熟记三角形内角和是是解题的关键.
设三角形三个内角的度数为,根据三角形内角和是求解即可.
【详解】解:设三角形三个内角的度数为,
∴,
解得,
∴最大角的度数.
故选:B.
5.B
【分析】本题主要考查三角形的内角和定理,通过方程求解,,的度数是解题的关键.由题意设,,,利用三角形的内角和定理可求解值,即可求解各内角的度数,再由折叠的性质可求得的度数,根据周角的定义可求解.
【详解】解:,
设,,,
,
解得,
,,,
由折叠可知:,
,
故选:B.
6.C
【分析】根据平行线的性质,可得,再由对顶角相等可得,从而得到,即可求解.
【详解】解:如图,
根据题意得:,
∴,
∴,
∴,
∴.
故选:C.
【点睛】本题主要考查了平行线的性质,对顶角相等,直角三角形两锐角互余,熟练掌握平行线的性质,直角三角形两锐角互余是解题的关键.
7.B
【分析】此题考查了余角和补角,根据垂直定义可得,然后再根据余角定义和补角定义进行分析即可求解,掌握互余和互补的定义是解题的关键.
【详解】解:、∵,,
∴,
∴,,
∴是的余角,也是的余角,故错误,不合题意;
、∵,,
∵,
∴,,,,
∴图中互余的角共有对,故正确,符合题意;
、∵,,
∴,
∵,
∴,
又∵,
∴的补角有和,故错误,不合题意;
、∵,
∴图中与互补的角共有个,故错误,不合题意;
故选:
8.D
【分析】根据题意先利用外角等于不相邻的两个内角之和,以及角平分线的性质求 ,再依此类推得, 找出规律,从而求的值.
【详解】解:根据题意得∠ACD=∠A+∠ABC.
∵∠ABC与∠ACD的平分线交于点A1,
= =,
同理可得
∴
故选D.
【点睛】本题为找规律题,主要考查三角形的外角性质及三角形的内角和定理,同时考查了角平分线的定义.解答的关键是沟通外角和内角的关系.
9.C
【分析】先证明,然后求出当时,,由此按照图①求解即可判断(1);当时, 求得,,则,即可判断(2);当时,先求出,则,,即可判断(3);根据题意当时,只有如图②一种情况,据此判断(4)即可.
【详解】解:当三角板旋转角度小于度时,如题干图②,设直线与直线交于F,
∴,
∴,
当时,即,如图①所示,
∴,
∴;
当三角板旋转角度大于时,如图②所示,
∴,
∴当时,即,
∴,
∴此时在图中的位置,
∴,故(1)正确;
当三角板旋转角度小于度时,如图所示,
当时,,
∴,
∴,
∴,
∴,
∴;
当三角板旋转角的大于时,如图④所示,
同理可得,
∴,
∴,
∵,
∴,故(2)错误;
如图⑤所示,当时,
∵,
∴,
∴,,
∴,
∴,故(3)正确;
由于顺时针旋转到B、C、E共线时停止,
∴当时,只有如下图⑥一种情况,
∴,
∴,
∴,
∴,故(4)正确,
故选:C.
【点睛】本题主要考查了三角板中角度的计算,三角形内角和定理,平行线的判定,正确理解题意是解题的关键.
10./66度
【分析】本题考查了三角形的内角和定理,平角的定义,根据三角形的内角和定理和平角的定义即可得到结论.
【详解】解:,,,
,
,
,
故答案为:.
11.90
【分析】如图,根据题意易得,进而根据三角形内角和可进行求解.
【详解】解:如图,
∵,,
∴,
∵,,
∴;
故答案为90.
【点睛】本题主要考查三角形内角和及平行线的性质,熟练掌握三角形内角和及平行线的性质是解题的关键.
12.等腰直角三角形
【分析】由三角形的三个内角度数比为1:1:2,可设三角形的三个内角分别为:x,x,2x,然后由三角形的内角和等于180°,即可得方程:x+x+2x=180°,解此方程即可求得答案.
【详解】∵三角形的三个内角度数比为1:1:2,
∴设三角形的三个内角分别为:x,x,2x,
∴x+x+2x=180°,
解得:x=45°,
∴三角形的三个内角度数分别为:45°,45°,90°.
∴这个三角形为等腰直角三角形.
故答案为等腰直角三角形.
【点睛】此题考查了三角形的内角和定理.此题比较简单,解题的关键是根据三角形的三个内角度数比为1:1:2,设三角形的三个内角分别为:x,x,2x,利用方程思想求解.
13.(如果少了或多了单位“°”,不算错)
【详解】试题解析:如图所示,
∵∠=∠,
∴∠=∠
∵∠=,∠=
∴∠=180°--
∴∠=(180°--)
∴∠DEA=(180°--)+=120°-
∴∠DAE=90°-(120°-)=.
故答案为:
14.30°或52.5°或80°.
【分析】分三种情况讨论,①当∠CDA=3∠C时,②当∠C=3∠CAD时,③∠CDA=3∠CAD时,由“和谐三角形”定义可求解;
【详解】解:∵,,
∴
①当∠CDA=3∠C时,∠CDA=90°,
∴∠CAD=60°,
∴∠BAD=30°;
②当∠C=3∠CAD时,
∴∠CAD=10°,
∴∠DAB=80°;
③∠CDA=3∠CAD时,
∴∠CAD=×(180°-30°)=37.5°,
∴∠DAB=52.5°,
故答案为:30°或52.5°或80°.
【点睛】本题是三角形综合题,考查了三角形内角和定理,理解“和谐三角形”定义,并能运用是解决本题的关键.
15.见解析
【分析】本题考查的是直角三角形的性质,可证明.在中,已知,等量代换可证是直角三角形,熟记直角三角形的判定定理是解题的关键.
【详解】证明:,
,
,
,
是直角三角形.
16.(1)图中有3个直角三角形,分别是,,
(2),理由见解析
【分析】(1)由题中已知条件,是高,可以得到、、都是直角.
(2)由(1)得到,,是直角三角形,且、、是直角,所以,由此可以得到.
【详解】(1) ,是高,
,
图中有个直角三角形,分别是,,;
(2) ,,是直角三角形,且、、是直角,
,,
.
【点睛】本题考查了直角三角形的两个锐角互余,三角形高的定义,熟练掌握直角三角形的定义是解题的关键.
17.(1)114
(2),证明见解析
(3)
【分析】本题考查对顶角性质、余角性质和平行线的性质,三角形内角和定理,熟练运用这些知识点是关键.
(1)先根据,,求出,再根据平行线的性质得出,最后求出结果即可;
(2)过点作,运用余角性质和平行线的性质分析即可;
(3)运用对顶角性质、三角形内角和定理和平行线的性质分析即可.
【详解】(1)解:如图1,
∵,,
∴,
∵,
∴,
∴,
故答案为:114;
(2)解:与的关系:.
证明:如图2,过点作,
由题意可知,,
∵
∴
∴,
,
∵
∴,
,
.
(3)解:.
证明:设与直线交于点,与直线交于点,
则,
∵,
∴,
,,
∴,
,
.
18.(1);(2);(3)
【分析】(1)由折叠得,又三角形外角性质,,所以得到 (2)由∠BMF+∠AMF=180°,将(1)结论代入即可得到关系;(3)由∠DEM+∠D+∠AMF=180°,结合前两问结论即可得关系
【详解】(1)∵沿折叠得到,∴.
∵,∴.
(2).
(3).
【点睛】本题主要考查折叠性质、三角形内角和定义与外角性质的简单应用,解题关键在于第一问的关系找出之后后续两问要结合前面结论
19.∠A=50°.
【详解】【试题分析】根据三角形内角和定理求解.
【试题解析】∠C=∠B-10°=20°+∠A-10°=10°+∠A,
所以∠A+∠B+∠C=∠A+20°+∠A+10°+∠A=3∠A+30°=180°,所以∠A=50°.
20.(1)∠AMC′=2∠ACB;(2)∠AMC′+∠BNC′=2∠ACB,理由见详解;(3)∠AMC′-∠BNC′=2∠ACB;(4)∠AMD′+∠BNC′=2(∠C+∠D)-360°.
【分析】(1)根据折叠性质和三角形的外角定理得出结论;
(2)先根据折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,由两个平角∠CMA和∠CNB得:∠AMC′+∠′BNC′等于360°与四个折叠角的差,化简为结果;
(3)利用两次外角定理得∠AMC′=∠C′+∠C+∠BNC′,然后根据等量代换,得出结论;
(4)与(2)类似,先由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,再由两平角的和为360°得:∠AMD′+∠BNC′=360°-2∠DMN-2∠CNM,根据四边形的内角和得:∠DMN+∠CNM=360°-∠C-∠D,代入前式可得结论.
【详解】解:(1)由折叠得:∠ACB=∠MC′C,
∵∠AMC′=∠ACB+∠MC′C,
∴∠AMC′=2∠ACB;
故答案为∠AMC′=2∠ACB;
(2)猜想:∠AMC′+∠BNC′=2∠ACB,
理由是:
由折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,
∵∠CMA+∠CNB=360°,
∴∠AMC′+∠′BNC′=360°-∠CMN-∠C′MN-∠CNM-∠C′NM=360°-2∠CMN-2∠CNM,
∴∠AMC′+∠BNC′=2(180°-∠CMN-∠CNM)=2∠ACB;
(3)∵∠AMC′=∠MDC+∠C,∠MDC=∠C′+∠BNC′,
∴∠AMC′=∠C′+∠BNC′+∠C,
∵∠C=∠C′,
∴∠AMC′=2∠C+∠BNC′,
∴∠AMC′-∠BNC′=2∠ACB;
故答案为∠AMC′-∠BNC′=2∠ACB;
(4)由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,
∵∠DMA+∠CNB=360°,
∴∠AMD′+∠BNC′=360°-2∠DMN-2∠CNM,
∵∠DMN+∠CNM=360°-∠C-∠D,
∴∠AMD′+∠BNC′=360°-2(360°-∠C-∠D)=2(∠C+∠D)-360°,
故答案为∠AMD′+∠BNC′=2(∠C+∠D)-360°.
【点睛】本题是折叠变换问题,思路分两类:①一类是利用外角定理得结论;②一类是利用平角和多边形内角和相结合得结论;字母书写要细心,角度比较复杂,是易错题.
11.2.1 三角形的内角同步练习
班级: 姓名:
同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你收获满满,学习进步,榜上有名!
一、单选题
1.如图,,被直线所截,且,平分,过点G作,若,则的度数为( )
A. B. C. D.
2.已知一个三角形三个内角度数的比是1:2:3,则其最大内角的度数为( )
A. B. C. D.
3.如图摆放的一副直角三角尺,,,与相交于点,当时,的度数是( )
A. B. C. D.
4.一个三角形的三个内角的度数比是,最大的角是( )
A. B. C.
5.如图,已知在中,,现将分别沿边翻折得到,则的度数为( )
A. B. C. D.
6.将一块三角板和一把直尺如图放置,若,则的度数为( )
A. B. C. D.
7.如图,已知点是射线上一点,过作交射线于点,交射线于点,下列结论正确的是( )
A.的余角只有 B.图中互余的角共有对
C.的补角只有 D.图中与互补的角共有个
8.如商,在△ABC中,∠A=α,∠ABC与∠ACD的平分钱交十点A1,得∠A1,∠A1BC与∠A1CD的平分线相交于点A2,得∠A2,……∠A6BC与∠A6CD的平分线相交于点A7,得∠A7,则∠A7=( )
A. B. C. D.
9.如图①,将一副三角板中的两个直角叠放在一起,其中,,,,现按住三角板不动,将三角板绕点C顺时针旋转,图②是旋转过程中的某一位置,当B、C、E三点第一次共线时旋转停止,记(k为常数),给出下列四个说法:
①当时,直线与直线相交所成的锐角度数为;
②当时,;
③当时,;
④当时,.其中正确的说法的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
10.如图,的顶点落在的边上,边,分别交的边于点E,F.若,,则的度数是
11.如图,直线,,,则的度数是 度.
12.一个三角形的三个内角的度数比为1:1:2,则这个三角形的形状为 .
13.已知在钝角△中,∠=>90°,∠=.为高,点在上,且∠=∠,则∠= (用含、的代数式表示).
14.若一个三角形中一个角的度数是另一个角的度数的3倍,则称这样的三角形为“和谐三角形”.例如,三个内角分别为,,的三角形是“和谐三角形”,如图,直角三角形中,,,是边上一动点.当是“和谐三角形”时,的度数是 .
三、解答题
15.如图所示,在中,.
求证:是直角三角形.
16.如图,在中,,是的高.
(1)图中有几个直角三角形?是哪几个?
(2)和有什么数量关系?并说明理由.
17.综合与实践
数学活动课上,老师先在黑板上画出两条直线,再将三角板(,与直线a相交于点A)放在黑板上,转动三角板得到下面三个不同位置的图形.
(1)【初步探究】
如图①,若点B在直线b上,,则________°;
(2)【深入探究】
如图②,若点B在直线a,b之间,与有怎样的数量关系?写出结论,并给出证明;
(3)【拓展延伸】
如图③,若点B在直线b的下方,请直接写出与之间的数量关系.
18.如图,点,分别是的边,上任意一点,将沿折叠至,已知.
(1)若已知,探究,,之间的关系.
(2)若已知,探究,,之间的关系(直接写出结论,不需要证明).
(3)若已知,探究,,之间的关系(直接写出结论,不需要证明).
19.在△ABC中,∠B=20°+∠A,∠C=∠B-10°,求∠A的度数.
20.如图 1,一张△ABC 纸片,点 M、N 分别是 AC、BC 上两点.
(1)若沿直线 MN 折叠,使 C 点落在 BN 上,则∠AMC′与∠ACB 的数量关系是 ;
(2)若折成图 2 的形状.猜想∠AMC′、∠BNC′和∠ACB 的数量关系,并说明理由.
猜想: .
理由:
(3)若折成图3 的形状,猜想∠AMC′、∠BNC′和∠ACB 的数量关系是 .(写出结论即可).
(4)将上述问题推广,如图4,将四边形 ABCD 纸片沿 MN 折叠,使点 C、D 落在四边形 ABNM 的内部时,∠AMD′+∠BNC′与∠C、∠D 之间的数量关系 是 (写出结论即可).
1.B
【分析】本题考查了平行线的性质,三角形的内角和定理以及角平分线的性质,正确熟练运用知识点进行角度计算是解答本题的关键.
先在中通过三角形内角和定理得出度数,再由平行线的性质求出的度数,最后由角平分线的性质即可求出答案.
【详解】解:∵,,
∴,
∵,
∴,
∴,
∵平分,
∴.
故选:B.
2.C
【分析】已知三角形三个内角的度数之比,可以设三个内角度数为:,,,根据三角形的内角和等于,列方程求三个内角的度数,确定最大的内角的度数.
【详解】解:设三个内角度数为:,,,
根据三角形内角和定理,可知,
解得:.
∴,即最大的内角是90°.
故选:C.
【点睛】本题考查了三角形内角和定理,解题的关键是见比设参.
3.B
【分析】本题主要考查了平行线的性质和三角形内角和定理.过点作,则有,,又因为和都是特殊直角三角形,,,可以得到,,进而可求解的度数,再根据平角的定义即可得出答案.
【详解】解:过点作,
∵,
∴,
,,
在和中,,,
,,
,,
,
,
,
故选:B.
4.B
【分析】此题考查了三角形内角和定理,熟记三角形内角和是是解题的关键.
设三角形三个内角的度数为,根据三角形内角和是求解即可.
【详解】解:设三角形三个内角的度数为,
∴,
解得,
∴最大角的度数.
故选:B.
5.B
【分析】本题主要考查三角形的内角和定理,通过方程求解,,的度数是解题的关键.由题意设,,,利用三角形的内角和定理可求解值,即可求解各内角的度数,再由折叠的性质可求得的度数,根据周角的定义可求解.
【详解】解:,
设,,,
,
解得,
,,,
由折叠可知:,
,
故选:B.
6.C
【分析】根据平行线的性质,可得,再由对顶角相等可得,从而得到,即可求解.
【详解】解:如图,
根据题意得:,
∴,
∴,
∴,
∴.
故选:C.
【点睛】本题主要考查了平行线的性质,对顶角相等,直角三角形两锐角互余,熟练掌握平行线的性质,直角三角形两锐角互余是解题的关键.
7.B
【分析】此题考查了余角和补角,根据垂直定义可得,然后再根据余角定义和补角定义进行分析即可求解,掌握互余和互补的定义是解题的关键.
【详解】解:、∵,,
∴,
∴,,
∴是的余角,也是的余角,故错误,不合题意;
、∵,,
∵,
∴,,,,
∴图中互余的角共有对,故正确,符合题意;
、∵,,
∴,
∵,
∴,
又∵,
∴的补角有和,故错误,不合题意;
、∵,
∴图中与互补的角共有个,故错误,不合题意;
故选:
8.D
【分析】根据题意先利用外角等于不相邻的两个内角之和,以及角平分线的性质求 ,再依此类推得, 找出规律,从而求的值.
【详解】解:根据题意得∠ACD=∠A+∠ABC.
∵∠ABC与∠ACD的平分线交于点A1,
= =,
同理可得
∴
故选D.
【点睛】本题为找规律题,主要考查三角形的外角性质及三角形的内角和定理,同时考查了角平分线的定义.解答的关键是沟通外角和内角的关系.
9.C
【分析】先证明,然后求出当时,,由此按照图①求解即可判断(1);当时, 求得,,则,即可判断(2);当时,先求出,则,,即可判断(3);根据题意当时,只有如图②一种情况,据此判断(4)即可.
【详解】解:当三角板旋转角度小于度时,如题干图②,设直线与直线交于F,
∴,
∴,
当时,即,如图①所示,
∴,
∴;
当三角板旋转角度大于时,如图②所示,
∴,
∴当时,即,
∴,
∴此时在图中的位置,
∴,故(1)正确;
当三角板旋转角度小于度时,如图所示,
当时,,
∴,
∴,
∴,
∴,
∴;
当三角板旋转角的大于时,如图④所示,
同理可得,
∴,
∴,
∵,
∴,故(2)错误;
如图⑤所示,当时,
∵,
∴,
∴,,
∴,
∴,故(3)正确;
由于顺时针旋转到B、C、E共线时停止,
∴当时,只有如下图⑥一种情况,
∴,
∴,
∴,
∴,故(4)正确,
故选:C.
【点睛】本题主要考查了三角板中角度的计算,三角形内角和定理,平行线的判定,正确理解题意是解题的关键.
10./66度
【分析】本题考查了三角形的内角和定理,平角的定义,根据三角形的内角和定理和平角的定义即可得到结论.
【详解】解:,,,
,
,
,
故答案为:.
11.90
【分析】如图,根据题意易得,进而根据三角形内角和可进行求解.
【详解】解:如图,
∵,,
∴,
∵,,
∴;
故答案为90.
【点睛】本题主要考查三角形内角和及平行线的性质,熟练掌握三角形内角和及平行线的性质是解题的关键.
12.等腰直角三角形
【分析】由三角形的三个内角度数比为1:1:2,可设三角形的三个内角分别为:x,x,2x,然后由三角形的内角和等于180°,即可得方程:x+x+2x=180°,解此方程即可求得答案.
【详解】∵三角形的三个内角度数比为1:1:2,
∴设三角形的三个内角分别为:x,x,2x,
∴x+x+2x=180°,
解得:x=45°,
∴三角形的三个内角度数分别为:45°,45°,90°.
∴这个三角形为等腰直角三角形.
故答案为等腰直角三角形.
【点睛】此题考查了三角形的内角和定理.此题比较简单,解题的关键是根据三角形的三个内角度数比为1:1:2,设三角形的三个内角分别为:x,x,2x,利用方程思想求解.
13.(如果少了或多了单位“°”,不算错)
【详解】试题解析:如图所示,
∵∠=∠,
∴∠=∠
∵∠=,∠=
∴∠=180°--
∴∠=(180°--)
∴∠DEA=(180°--)+=120°-
∴∠DAE=90°-(120°-)=.
故答案为:
14.30°或52.5°或80°.
【分析】分三种情况讨论,①当∠CDA=3∠C时,②当∠C=3∠CAD时,③∠CDA=3∠CAD时,由“和谐三角形”定义可求解;
【详解】解:∵,,
∴
①当∠CDA=3∠C时,∠CDA=90°,
∴∠CAD=60°,
∴∠BAD=30°;
②当∠C=3∠CAD时,
∴∠CAD=10°,
∴∠DAB=80°;
③∠CDA=3∠CAD时,
∴∠CAD=×(180°-30°)=37.5°,
∴∠DAB=52.5°,
故答案为:30°或52.5°或80°.
【点睛】本题是三角形综合题,考查了三角形内角和定理,理解“和谐三角形”定义,并能运用是解决本题的关键.
15.见解析
【分析】本题考查的是直角三角形的性质,可证明.在中,已知,等量代换可证是直角三角形,熟记直角三角形的判定定理是解题的关键.
【详解】证明:,
,
,
,
是直角三角形.
16.(1)图中有3个直角三角形,分别是,,
(2),理由见解析
【分析】(1)由题中已知条件,是高,可以得到、、都是直角.
(2)由(1)得到,,是直角三角形,且、、是直角,所以,由此可以得到.
【详解】(1) ,是高,
,
图中有个直角三角形,分别是,,;
(2) ,,是直角三角形,且、、是直角,
,,
.
【点睛】本题考查了直角三角形的两个锐角互余,三角形高的定义,熟练掌握直角三角形的定义是解题的关键.
17.(1)114
(2),证明见解析
(3)
【分析】本题考查对顶角性质、余角性质和平行线的性质,三角形内角和定理,熟练运用这些知识点是关键.
(1)先根据,,求出,再根据平行线的性质得出,最后求出结果即可;
(2)过点作,运用余角性质和平行线的性质分析即可;
(3)运用对顶角性质、三角形内角和定理和平行线的性质分析即可.
【详解】(1)解:如图1,
∵,,
∴,
∵,
∴,
∴,
故答案为:114;
(2)解:与的关系:.
证明:如图2,过点作,
由题意可知,,
∵
∴
∴,
,
∵
∴,
,
.
(3)解:.
证明:设与直线交于点,与直线交于点,
则,
∵,
∴,
,,
∴,
,
.
18.(1);(2);(3)
【分析】(1)由折叠得,又三角形外角性质,,所以得到 (2)由∠BMF+∠AMF=180°,将(1)结论代入即可得到关系;(3)由∠DEM+∠D+∠AMF=180°,结合前两问结论即可得关系
【详解】(1)∵沿折叠得到,∴.
∵,∴.
(2).
(3).
【点睛】本题主要考查折叠性质、三角形内角和定义与外角性质的简单应用,解题关键在于第一问的关系找出之后后续两问要结合前面结论
19.∠A=50°.
【详解】【试题分析】根据三角形内角和定理求解.
【试题解析】∠C=∠B-10°=20°+∠A-10°=10°+∠A,
所以∠A+∠B+∠C=∠A+20°+∠A+10°+∠A=3∠A+30°=180°,所以∠A=50°.
20.(1)∠AMC′=2∠ACB;(2)∠AMC′+∠BNC′=2∠ACB,理由见详解;(3)∠AMC′-∠BNC′=2∠ACB;(4)∠AMD′+∠BNC′=2(∠C+∠D)-360°.
【分析】(1)根据折叠性质和三角形的外角定理得出结论;
(2)先根据折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,由两个平角∠CMA和∠CNB得:∠AMC′+∠′BNC′等于360°与四个折叠角的差,化简为结果;
(3)利用两次外角定理得∠AMC′=∠C′+∠C+∠BNC′,然后根据等量代换,得出结论;
(4)与(2)类似,先由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,再由两平角的和为360°得:∠AMD′+∠BNC′=360°-2∠DMN-2∠CNM,根据四边形的内角和得:∠DMN+∠CNM=360°-∠C-∠D,代入前式可得结论.
【详解】解:(1)由折叠得:∠ACB=∠MC′C,
∵∠AMC′=∠ACB+∠MC′C,
∴∠AMC′=2∠ACB;
故答案为∠AMC′=2∠ACB;
(2)猜想:∠AMC′+∠BNC′=2∠ACB,
理由是:
由折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,
∵∠CMA+∠CNB=360°,
∴∠AMC′+∠′BNC′=360°-∠CMN-∠C′MN-∠CNM-∠C′NM=360°-2∠CMN-2∠CNM,
∴∠AMC′+∠BNC′=2(180°-∠CMN-∠CNM)=2∠ACB;
(3)∵∠AMC′=∠MDC+∠C,∠MDC=∠C′+∠BNC′,
∴∠AMC′=∠C′+∠BNC′+∠C,
∵∠C=∠C′,
∴∠AMC′=2∠C+∠BNC′,
∴∠AMC′-∠BNC′=2∠ACB;
故答案为∠AMC′-∠BNC′=2∠ACB;
(4)由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,
∵∠DMA+∠CNB=360°,
∴∠AMD′+∠BNC′=360°-2∠DMN-2∠CNM,
∵∠DMN+∠CNM=360°-∠C-∠D,
∴∠AMD′+∠BNC′=360°-2(360°-∠C-∠D)=2(∠C+∠D)-360°,
故答案为∠AMD′+∠BNC′=2(∠C+∠D)-360°.
【点睛】本题是折叠变换问题,思路分两类:①一类是利用外角定理得结论;②一类是利用平角和多边形内角和相结合得结论;字母书写要细心,角度比较复杂,是易错题.
