3.1.1 函数的概念 教学设计
文档属性
| 名称 | 3.1.1 函数的概念 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 229.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-24 15:47:35 | ||
图片预览



文档简介
教学设计 函数的概念
(一)课时教学内容
函数的概念。
(二)课时教学目标
1.在归纳概括集合间的对应关系,抽象出函数概念后,能区分此函数概念与初中的函数概念的不同,会说出已学过的简单函数的定义域、对应关系与值域三要素;
2.理解对应关系是不依赖于表示方式而客观存在的,其实质是对于定义域的任一值,通过对应关系都能得出唯一对应的函数值。知道对应关系的表示常用解析式、图像与表格;
3.对于函数的表示法解析式和图像,能通过函数解析式画出函数的图像,也能通过函数的图像理解并写出解析式,可以使学生既加深对函数对应关系的理解,有培养数形结合思想,发展直观想象素养。
函数是具有一般意义的抽象概念,是概念性知识,需要学生理解,而不是记忆。教学过程中应通过实例引发学生思考,尝试表达,提出疑问等,加深学生对概念的理解。概念的学习过程是学生主动建构知识的过程;
(三)教学重点与难点
教学重点:由实例归纳、概括函数的基本特征,用集合与对应关系表达函数的概念,用适当的方法表示函数;
教学难点:从生活实例中归纳、概括、抽象出函数概念,用集合语言和对应关系理解具体问题中的函数关系。突破难点主要通过比较不同实例,归纳概括共同点,让学生尝试表达,抽象出函数的三要素,体会“对应”是函数概念的重要特征。
(四)教学过程设计
环节一、情景引入,温故知新
在初中,我们已经学习了函数的定义为:在一个变化过程中,如果有两个变量与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么我们称是自变量,是的函数.
问题1:(1)你能用已学的函数知识判断与是否为相同的函数吗
(2)正方形的周长与边长的对应关系为,而且对于的每一个确定的值,都有唯一确定的值与其对应,所以是的函数.请问这个函数与正比例函数是同一个函数吗
【设计意图】带领学生复习初中“变量说”的函数概念,以问题引起认知冲突,激发学生的求知欲,体现进一步研究函数的必要性.
环节二、抽象概念,内涵辨析
问题2:某“复兴号”高速列车加速到后保持匀速运行半小时.
(1)这段时间内,列车行进的路程(单位:)与运行时间(单位:h)的关系如何表示 这是一个函数吗 请说明理由.
(2)有同学想:“根据对应关系,这趟列车加速到后,运行就前进了.”这位同学的想法正确吗
(3)如何更加精准地表述与的函数关系
【设计意图】教师给出问题(1)后,请学生自己思考并回答,提醒学生不看教科书.教师点评答案,引导学生用已学的变量关系刻画这个函数.
对问题(2)请学生在信息技术平台上提交答案,并邀请学生说出判断的理由,教师点评并引导学生认识到必须关注自变量的取值范围.
对问题(3)引导学生体会“更加精确地表述”需要确定自变量的范围,得到集合,再类比初中的函数概念,描述这个函数关系,教师要在学生思考和讨论的基础上给出精确表述的示范.
问题3:某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么:
(1)你认为应该怎样确定一个工人每周所得的工资
(2)一个工人的工资是他工作天数的函数吗 请说明理由.
(3)你能仿照问题(1)中对和的对应关系的精准刻画,给出这个问题中与的精准表示吗
【设计意图】对问题(1)学生给出的答案可能大部分都是,教师需要引导学生还可以用不同的表示方法,例如列表格的形式.
对问题(2)设计为判断题,学生可以在信息平台上给出自己的答案.
对问题(3)可以让学生模仿问题1的方法给出表述,教师通过信息技术平台展示学生的答案,然后点评学生回答情况并给出严谨规范的表述.
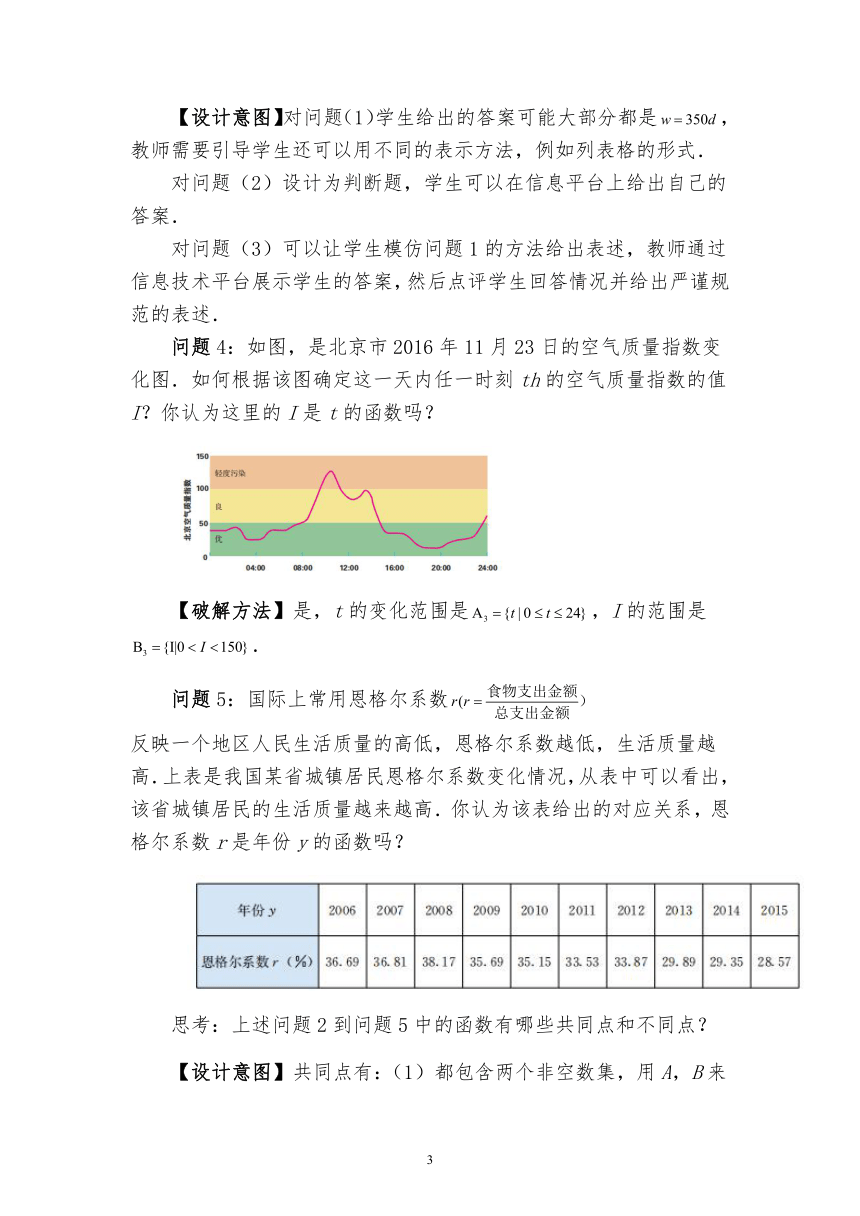
问题4:如图,是北京市2016年11月23日的空气质量指数变化图.如何根据该图确定这一天内任一时刻th的空气质量指数的值I?你认为这里的I是t的函数吗?
【破解方法】是,t的变化范围是,I的范围是.
问题5:国际上常用恩格尔系数 反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高.上表是我国某省城镇居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来越高.你认为该表给出的对应关系,恩格尔系数r是年份y的函数吗?
思考:上述问题2到问题5中的函数有哪些共同点和不同点?
【设计意图】共同点有:(1)都包含两个非空数集,用A,B来表示;(2)都有一个对应关系.
不同点有:问题2,3是通过解析式表示对应关系,问题4是通过图象,问题5是通过表格
【归纳新知】
1、函数的概念
设A、B是非空的数集,如果按照某个确定的对应关系,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数和它对应,那么就称为从集合A到集合B的一个函数.
记作:,.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.
知识点诠释:
(1)A、B集合的非空性;(2)对应关系的存在性、唯一性、确定性;(3)A中元素的无剩余性;(4)B中元素的可剩余性.
2、构成函数的三要素:定义域、对应关系和值域
①构成函数的三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全—致,即称这两个函数相等(或为同一函数);
②两个函数相等当且仅当它们的定义域和对应关系完全—致,而与表示自变量和函数值的字母无关.
问题6:函数的三要素为定义域、对应关系和值域,定义域和值域都是非空数集.在数学中有没有刻画非空数集的简单方式呢?请大家阅读教科书第64页相关内容.
(1)什么叫闭区间?什么叫开区间?什么叫半开半闭区间?
(2)区间的端点应满足什么条件?0
(3)请用区间表示实数集R.书写带有“+∞”、“-∞”的区间时,应使用小括号还是中括号?
【设计意图】教师先让学生阅读并独立思考,尝试理解有关概念和相应记法,然后提出上述3个问题,检验学生自主阅读和理解能力,并提醒学生先不要看教科书第65页.
【归纳新知】
3、区间的概念
(1)区间的分类:开区间、闭区间、半开半闭区间;
(2)无穷区间;
(3)区间的数轴表示.
区间表示:
;
; ;
; .
环节三、理解概念,例题落实
例1.求下列函数的定义域:
⑴;
解:因为函数有意义当且仅当解得,且,所以函数定义域为.
⑵.
解:因为函数有意义当且仅当解得,且,所以函数定义域为.
【设计意图】总结⑴求函数定义域常用依据:①分式中分母不能为零;②二次根式中被开方数要大于或等于零;③零次幂的底数不能为零。提出⑵常见错误:把函数化为再求定义域,引起学生注意。
例2. 判断下列各组函数是否为同一个函数:
⑴,;(不是,定义域不同)
⑵,;(不是,对应关系不同)
⑶,. (是,定义域和对应关系均相同)
【设计意图】学生解答,让学生明确函数三要素是判断同一函数的标准。如果两个函数的定义域相同,对应关系也相同(则值域一定也相同),那么这两个函数就是同一个函数.
说明:在表示函数时,如果不会产生歧义,函数的定义域通常不写,此时就约定:函数的定义域就是使得这个函数有意义的所有实数组成的集合. 如函数,就是函数,,函数,就是函数,
例3.已知函数.
⑴求的值;
⑵当时,求值域.
解:⑴由已知可得
,,.
⑵因为,其图象为开口向上的抛物线且对称轴为,
所以当时,函数有最小值为,
又由⑴知,,所以当时,函数有最大值为.
综上所述,函数的值域为.
【设计意图】求函数值域的一种常用方法是画出函数图像,根据定义域观察截取函数图像,进而求得函数值域.
环节四、归纳小结,总结提升
问题7:请你带着下列问题回顾本节课学习的内容:
(1)函数的定义是什么 其三要素是什么
(2)你是怎么理解对应关系的
(3)与初中的函数概念相比较,你对函数有哪些新的认识
(4)函数的三种表示法:解析法、列表法和图象法各有什么优点
(5)如何理解分段函数
【设计意图】学生独立思考并请代表发言,再请其他同学补充,教师引导学生一起得出结论.
(五)目标检测设计
环节五:目标检测,检验效果
1.下列等式中的变量不具有函数关系的是( )
A. B.
C. D.
【答案】D
【检测目标】函数定义的理解;
2.下列集合不能用区间的形式表示的个数为( )
①;②;③;④;⑤;⑥.
A.2 B.3 C.4 D.5
【答案】D
【检测目标】函数定义的理解;
3.下列各组函数是同一函数的是( )
①与.②与.③与.④与.
A.①② B.①③ C.③④ D.①④
【答案】C
【检测目标】函数定义的理解,同一函数的辨别;
4.函数的定义域是 .
【答案】
【检测目标】函数定义域的理解;
5.已知
(1)求和;
(2)求函数的值域.
【解析】(1)由函数,
可得,,.
(2)函数的值域为.
【检测目标】函数值和值域的理解;
【设计意图】落实与理解教材要求的基本教学内容.
环节六:布置作业,应用迁移
作业:书后习题
【设计意图】掌握函数的概念,巩固本节课的知识点.
6
(一)课时教学内容
函数的概念。
(二)课时教学目标
1.在归纳概括集合间的对应关系,抽象出函数概念后,能区分此函数概念与初中的函数概念的不同,会说出已学过的简单函数的定义域、对应关系与值域三要素;
2.理解对应关系是不依赖于表示方式而客观存在的,其实质是对于定义域的任一值,通过对应关系都能得出唯一对应的函数值。知道对应关系的表示常用解析式、图像与表格;
3.对于函数的表示法解析式和图像,能通过函数解析式画出函数的图像,也能通过函数的图像理解并写出解析式,可以使学生既加深对函数对应关系的理解,有培养数形结合思想,发展直观想象素养。
函数是具有一般意义的抽象概念,是概念性知识,需要学生理解,而不是记忆。教学过程中应通过实例引发学生思考,尝试表达,提出疑问等,加深学生对概念的理解。概念的学习过程是学生主动建构知识的过程;
(三)教学重点与难点
教学重点:由实例归纳、概括函数的基本特征,用集合与对应关系表达函数的概念,用适当的方法表示函数;
教学难点:从生活实例中归纳、概括、抽象出函数概念,用集合语言和对应关系理解具体问题中的函数关系。突破难点主要通过比较不同实例,归纳概括共同点,让学生尝试表达,抽象出函数的三要素,体会“对应”是函数概念的重要特征。
(四)教学过程设计
环节一、情景引入,温故知新
在初中,我们已经学习了函数的定义为:在一个变化过程中,如果有两个变量与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么我们称是自变量,是的函数.
问题1:(1)你能用已学的函数知识判断与是否为相同的函数吗
(2)正方形的周长与边长的对应关系为,而且对于的每一个确定的值,都有唯一确定的值与其对应,所以是的函数.请问这个函数与正比例函数是同一个函数吗
【设计意图】带领学生复习初中“变量说”的函数概念,以问题引起认知冲突,激发学生的求知欲,体现进一步研究函数的必要性.
环节二、抽象概念,内涵辨析
问题2:某“复兴号”高速列车加速到后保持匀速运行半小时.
(1)这段时间内,列车行进的路程(单位:)与运行时间(单位:h)的关系如何表示 这是一个函数吗 请说明理由.
(2)有同学想:“根据对应关系,这趟列车加速到后,运行就前进了.”这位同学的想法正确吗
(3)如何更加精准地表述与的函数关系
【设计意图】教师给出问题(1)后,请学生自己思考并回答,提醒学生不看教科书.教师点评答案,引导学生用已学的变量关系刻画这个函数.
对问题(2)请学生在信息技术平台上提交答案,并邀请学生说出判断的理由,教师点评并引导学生认识到必须关注自变量的取值范围.
对问题(3)引导学生体会“更加精确地表述”需要确定自变量的范围,得到集合,再类比初中的函数概念,描述这个函数关系,教师要在学生思考和讨论的基础上给出精确表述的示范.
问题3:某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么:
(1)你认为应该怎样确定一个工人每周所得的工资
(2)一个工人的工资是他工作天数的函数吗 请说明理由.
(3)你能仿照问题(1)中对和的对应关系的精准刻画,给出这个问题中与的精准表示吗
【设计意图】对问题(1)学生给出的答案可能大部分都是,教师需要引导学生还可以用不同的表示方法,例如列表格的形式.
对问题(2)设计为判断题,学生可以在信息平台上给出自己的答案.
对问题(3)可以让学生模仿问题1的方法给出表述,教师通过信息技术平台展示学生的答案,然后点评学生回答情况并给出严谨规范的表述.
问题4:如图,是北京市2016年11月23日的空气质量指数变化图.如何根据该图确定这一天内任一时刻th的空气质量指数的值I?你认为这里的I是t的函数吗?
【破解方法】是,t的变化范围是,I的范围是.
问题5:国际上常用恩格尔系数 反映一个地区人民生活质量的高低,恩格尔系数越低,生活质量越高.上表是我国某省城镇居民恩格尔系数变化情况,从表中可以看出,该省城镇居民的生活质量越来越高.你认为该表给出的对应关系,恩格尔系数r是年份y的函数吗?
思考:上述问题2到问题5中的函数有哪些共同点和不同点?
【设计意图】共同点有:(1)都包含两个非空数集,用A,B来表示;(2)都有一个对应关系.
不同点有:问题2,3是通过解析式表示对应关系,问题4是通过图象,问题5是通过表格
【归纳新知】
1、函数的概念
设A、B是非空的数集,如果按照某个确定的对应关系,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数和它对应,那么就称为从集合A到集合B的一个函数.
记作:,.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.
知识点诠释:
(1)A、B集合的非空性;(2)对应关系的存在性、唯一性、确定性;(3)A中元素的无剩余性;(4)B中元素的可剩余性.
2、构成函数的三要素:定义域、对应关系和值域
①构成函数的三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全—致,即称这两个函数相等(或为同一函数);
②两个函数相等当且仅当它们的定义域和对应关系完全—致,而与表示自变量和函数值的字母无关.
问题6:函数的三要素为定义域、对应关系和值域,定义域和值域都是非空数集.在数学中有没有刻画非空数集的简单方式呢?请大家阅读教科书第64页相关内容.
(1)什么叫闭区间?什么叫开区间?什么叫半开半闭区间?
(2)区间的端点应满足什么条件?0
(3)请用区间表示实数集R.书写带有“+∞”、“-∞”的区间时,应使用小括号还是中括号?
【设计意图】教师先让学生阅读并独立思考,尝试理解有关概念和相应记法,然后提出上述3个问题,检验学生自主阅读和理解能力,并提醒学生先不要看教科书第65页.
【归纳新知】
3、区间的概念
(1)区间的分类:开区间、闭区间、半开半闭区间;
(2)无穷区间;
(3)区间的数轴表示.
区间表示:
;
; ;
; .
环节三、理解概念,例题落实
例1.求下列函数的定义域:
⑴;
解:因为函数有意义当且仅当解得,且,所以函数定义域为.
⑵.
解:因为函数有意义当且仅当解得,且,所以函数定义域为.
【设计意图】总结⑴求函数定义域常用依据:①分式中分母不能为零;②二次根式中被开方数要大于或等于零;③零次幂的底数不能为零。提出⑵常见错误:把函数化为再求定义域,引起学生注意。
例2. 判断下列各组函数是否为同一个函数:
⑴,;(不是,定义域不同)
⑵,;(不是,对应关系不同)
⑶,. (是,定义域和对应关系均相同)
【设计意图】学生解答,让学生明确函数三要素是判断同一函数的标准。如果两个函数的定义域相同,对应关系也相同(则值域一定也相同),那么这两个函数就是同一个函数.
说明:在表示函数时,如果不会产生歧义,函数的定义域通常不写,此时就约定:函数的定义域就是使得这个函数有意义的所有实数组成的集合. 如函数,就是函数,,函数,就是函数,
例3.已知函数.
⑴求的值;
⑵当时,求值域.
解:⑴由已知可得
,,.
⑵因为,其图象为开口向上的抛物线且对称轴为,
所以当时,函数有最小值为,
又由⑴知,,所以当时,函数有最大值为.
综上所述,函数的值域为.
【设计意图】求函数值域的一种常用方法是画出函数图像,根据定义域观察截取函数图像,进而求得函数值域.
环节四、归纳小结,总结提升
问题7:请你带着下列问题回顾本节课学习的内容:
(1)函数的定义是什么 其三要素是什么
(2)你是怎么理解对应关系的
(3)与初中的函数概念相比较,你对函数有哪些新的认识
(4)函数的三种表示法:解析法、列表法和图象法各有什么优点
(5)如何理解分段函数
【设计意图】学生独立思考并请代表发言,再请其他同学补充,教师引导学生一起得出结论.
(五)目标检测设计
环节五:目标检测,检验效果
1.下列等式中的变量不具有函数关系的是( )
A. B.
C. D.
【答案】D
【检测目标】函数定义的理解;
2.下列集合不能用区间的形式表示的个数为( )
①;②;③;④;⑤;⑥.
A.2 B.3 C.4 D.5
【答案】D
【检测目标】函数定义的理解;
3.下列各组函数是同一函数的是( )
①与.②与.③与.④与.
A.①② B.①③ C.③④ D.①④
【答案】C
【检测目标】函数定义的理解,同一函数的辨别;
4.函数的定义域是 .
【答案】
【检测目标】函数定义域的理解;
5.已知
(1)求和;
(2)求函数的值域.
【解析】(1)由函数,
可得,,.
(2)函数的值域为.
【检测目标】函数值和值域的理解;
【设计意图】落实与理解教材要求的基本教学内容.
环节六:布置作业,应用迁移
作业:书后习题
【设计意图】掌握函数的概念,巩固本节课的知识点.
6
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
