第十二章 全等三角形 习题课件(共128张PPT) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 第十二章 全等三角形 习题课件(共128张PPT) 2024-2025学年数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 10:25:25 | ||
图片预览











文档简介
(共128张PPT)
第1课时 全等三角形
第十二章 全等三角形
一、选择题
1.下列图形中,与如图所示图形全等的是( D )
第1题图
A
B
C
D
D
2.如图,已知△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( C )
A.6cm B.5cm
C.7cm D.无法确定
第2题图
3.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( C )
A.AC=CE B.∠BAC=∠ECD
C.∠ACB=∠ECD D.∠B=∠D
第3题图
C
C
4.如图所示的两个三角形全等,则∠α的度数是( C )
A.58° B.72° C.50° D.60°
第4题图
C
5.如图,已知△ABC≌△DEF,CD平分∠BCA,FD交BC于G,若∠A=28°,∠CGF=85°,则∠E的度数是( A )
A.38° B.36° C.34° D.32°
第5题图
A
二、填空题
6.若△ABC≌△A'B'C',∠A=60°,∠B=40°,则∠C'= 80° .
7.如图,若△ABC≌△DEF,则x= 20 .
第7题图
80°
20
三、解答题
8.如图,△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,写出其他对应边及对应角.
第8题图
解:∵△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,
∴AC=AE,BC=DE,∠C=∠E,∠BAC=∠DAE,
即AC和AE,BC和DE是对应边,
∠C和∠E,∠BAC和∠DAE是对应角.
9.如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若EB⊥AD,∠F=62°,求∠A的度数;
解:(1)∵EB⊥AD,∴∠EBD=90°,
∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,
∵∠F=62°,∴∠A=90°-∠F=28°;
第9题图
(2)若AD=9cm,BC=5cm,求AB的长.
解:(2)∵△ACF≌△DBE,∴CA=BD,
∴CA-CB=BD-BC,即AB=CD,
∵AD=9cm,BC=5cm,
∴AB+CD=4cm,
∴AB=2cm.
一、填空题
10.三个全等三角形按如图所示的方式摆放,则∠1+∠2+∠3的度数是 180° .
第10题图
180°
第11题图
11.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为 135° .
135°
二、解答题
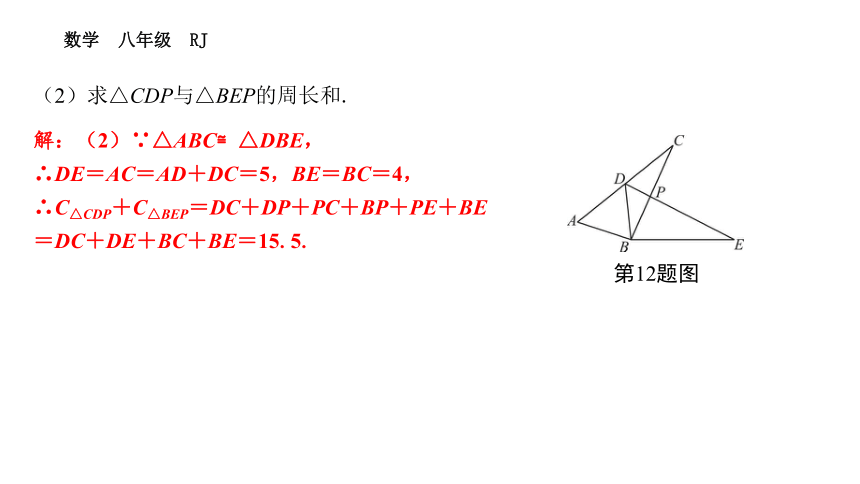
12.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数;
解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=∠ABE-∠DBC=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
第12题图
(2)求△CDP与△BEP的周长和.
解:(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴C△CDP+C△BEP=DC+DP+PC+BP+PE+BE
=DC+DE+BC+BE=15.5.
第12题图
解答题
13.如图所示,已知A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)BD、DE、CE之间有怎样的数量关系?请说明理由;
解:(1)BD=DE+CE,
理由:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
第13题图
(2)请你猜想当△ABD满足什么条件时,BD∥CE?并证明你的猜想.
解:(2)当△ABD满足∠ADB=90°时,BD∥CE,
证明:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180°-∠ADB=90°=∠E,
∴BD∥CE.
第13题图
谢 谢 观 看
第2课时 三角形全等的判定(1)
第十二章 全等三角形
一、选择题
1.如图,在△ABC中,AB=AC,BE=CE,则直接由“SSS”可以判定( C )
第1题图
A.△ABD≌△ACD B.△BDE≌△CDE
C.△ABE≌△ACE D.以上都不对
C
2.如图,AD=BC,AC=BD,AC与BD交于点E,则图中可以用“SSS”判定全等的三角形共有( C )
A.1对 B.2对 C.3对 D.4对
第2题图
C
二、填空题
3.如图,AB=DC,AC与DB相交于点O,要使△ABC≌△DCB,则应添加条件 AC=DB .(写出一个条件即可)
第3题图
AC=DB
4.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH,小明是通过识别全等三角形的方法得到的结论,则小明用的识别方法是 SSS .(用字母表示)
第4题图
SSS
三、解答题
5.如图,C是AB的中点,AD=CE,CD=BE.试说明:△ACD≌△CBE.
第5题图
证明:∵C是AB的中点,
∴AC=CB,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SSS).
6.如图所示,已知点A,E,F,C在同一条直线上,AB=CD,BF=DE,AE=CF.
求证:△ABF≌△CDE.
第6题图
证明:∵AE=CF,∴AF=CE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SSS).
7.如图,点D,E分别在边AC,AB上,且BE=CD,连接BD,CE,且BD=CE.
求证:△EBC≌△DCB.
第7题图
证明:在△EBC与△DCB中,
,
∴△EBC≌△DCB(SSS).
8.如图,点A、B、C、D在一条直线上,AC=DB,AE=DF,BE=CF.
(1)求证:∠E=∠F;
证明:(1)∵AC=DB,∴AB=DC,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SSS),
∴∠E=∠F;
第8题图
(2)求证:AE∥DF.
证明:(2)由(1)知△ABE≌△DCF,
∴∠A=∠D,
∴AE∥DF.
一、填空题
9.如图,AB=AC,BD=CD,∠BAC=50°,∠B=40°,则∠ADC= 115° .
第9题图
115°
二、解答题
10.如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC,求证:∠A=∠C,且点O在∠AEC的平分线上.
第10题图
证明:如图,连接OE,
在△AOE和△COE中,
,
∴△AOE≌△COE(SSS),
∴∠A=∠C,∠AEO=∠CEO,
∴OE平分∠AEC,
即点O在∠AEC的平分线上.
解答题
11.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证:∠ACB=∠AFB.
第11题图
证明:在△ABC和△DEB中,,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE,
∵∠AFB=∠ACB+∠DBE=2∠ACB,
∴∠ACB=∠AFB.
谢 谢 观 看
第3课时 三角形全等的判定(2)
第十二章 全等三角形
一、选择题
1.如图,AD,BC相交于点O,且AO=DO,BO=CO,则△ABO≌△DCO,理由是( B )
A.SSS B.SAS C.ASA D.AAS
第1题图
B
2.如图,已知OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC=( A )
A.95° B.120° C.50° D.105°
第2题图
A
二、填空题
3.如图所示,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,若能用“SAS”说明△ABC≌△DEF,则需要添加一个适当的条件是 AC=DF .
第3题图
AC=DF
第4题图
4.如图,要测量池塘AB的宽度,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘AB的宽为 25 m.
25
5.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,∠BAD=22°,∠ACE=30°,则∠ADE= 52° .
第5题图
52°
三、解答题
6.如图,点B是线段AD上一点,BC∥DE,AB=ED,BC=DB,
求证:△ABC≌△EDB.
第6题图
证明:∵BC∥DE,∴∠ABC=∠D,
在△ABC和△EDB中,
,
∴△ABC≌△EDB(SAS).
7.如图,在△ABC中,点D、E分别在AB、AC上,AB=AC,BD=CE,BE与CD交于点O.求证:∠ABE=∠ACD.
第7题图
证明:∵AB=AC,BD=CE,
∴AD=AE,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD.
8.如图,点C在线段AB上,△ACM与△CBN都是等边三角形,AN与MB交于点P.
求证:AN=BM.
第8题图
证明:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°,
∴∠ACN=∠MCB,
在△ACN和△MCB中,,
∴△ACN≌△MCB(SAS),
∴AN=BM.
一、选择题
9.如图,在平面直角坐标系中,点A(2,0),B(0,4),若△BOC与△ABO全等,则点C的坐标不能为( A )
A.(0,-4) B.(-2,0)
C.(2,4) D.(-2,4)
第9题图
A
10.如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF=( B )
A.90°-∠A B.90°-∠A
C.180°-2∠A D.45°-∠A
第10题图
B
二、解答题
11.将两个大小不同的等腰直角三角板按如图1所示放置,图2是由它抽象出的几何图形,点B、C、E在同一条直线上,连接DC.
(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(1)解:△ABE≌△ACD,证明如下:
∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
在△ABE与△ACD中,,
∴△ABE≌△ACD(SAS);
第11题图
(2)证明:DC⊥BE.
(2)证明:由(1)得∠ACD=∠ABE=45°,
∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
第11题图
解答题
12.在△ABC中,AD是BC边上的中线,AB=5cm,AD=3cm,求AC长度的取值范围.
解:如图,延长AD到点E,使得AD=DE,连接BE,
∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,
,
∴△BDE≌△CDA(SAS),∴BE=AC,
∵AD=3cm,DA=DE,
∴AE=6cm,
∵AB=5cm,
∴AE-AB<BE<AB+AE,
即1cm<BE<11cm,
∴1cm<AC<11cm.
谢 谢 观 看
第4课时 三角形全等的判定(3)
第十二章 全等三角形
一、选择题
1.如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,则△APD与△APE全等的依据是( B )
A.SAS B.AAS C.SSS D.ASA
第1题图
B
2.如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( A )
A.∠A=∠D B.AB=DE
C.∠A=∠E D.∠B=∠E
第2题图
3.在Rt△ABC与Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠B',AB=B'A',则下列结论正确的是( C )
A.AB=A'C' B.BC=B'C'
C.AC=B'C' D.∠A=∠A'
A
C
二、填空题
4.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,∠B=∠C,若AB=6,BE=4,则CD= 4 .
第4题图
4
第5题图
5.如图,在△ABC中,∠ABC=45°,F是高AD和高BE的交点,CD=4,则线段DF的长度为 4 .
4
三、解答题
6.如图,已知CE⊥AB于点E,BF⊥AC于点F,BF交CE于点D,且AB=AC,求证:△ABF≌△ACE.
第6题图
证明:∵CE⊥AB,BF⊥AC,
∴∠AFB=∠AEC=90°,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(AAS).
7.如图,在△ABC中,∠B=∠C=∠EDF=50°,DE=DF,BE=5,CF=2,
求BC的长.
第7题图
解:∵∠B=∠C=∠EDF=50°,∠EDC=∠EDF+∠FDC=∠B+∠DEB,
∴∠FDC=∠DEB,
∵DE=FD,
∴△BED≌△CDF(AAS),
∴BD=CF=2,BE=CD=5,
∴BC=BD+CD=7.
8.如图,在△ABC中,E是AC的中点,点F在AB上,CD∥AB,交FE的延长线于点D.
(1)求证:EF=ED;
(1)证明:∵CD∥AB,∴∠A=∠ECD,
∵E是AC的中点,∴AE=CE,
在△AEF和△CED中,,
∴△AEF≌△CED(ASA),
∴EF=ED;
第8题图
(2)若AB=8,CD=6,求BF的长.
(2)解:由(1)知,△AEF≌△CED,∴AF=CD=6,
∴BF=AB-AF=2.
第8题图
一、选择题
9.如图,在平面直角坐标系中,点A的坐标为(2,3),且AO=BO,∠AOB=90°,则点B的坐标为( B )
A.(2,3) B.(-3,2)
C.(-3,-2) D.(-2,3)
第9题图
B
二、填空题
10.如图,点D,E在△ABC的BC边上,∠BAD=∠CAE,要推理得出△ABE≌△ACD,可以补充的一个条件是 AB=AC(答案不唯一) .(不添加辅助线,写出一个即可)
第10题图
AB=AC(答案不唯一)
三、解答题
11.如图,在△ABC与△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB于点F,AB=DE.
(1)求证:BC=DB;
第11题图
(1)证明:∵DE⊥AB,
∴∠BFE=90°,
∴∠ABC+∠DEB=90°,
∵∠ACB=90°,
∴∠ABC+∠A=90°,
∴∠A=∠DEB,
在△ABC和△EDB中,,
∴△ABC≌△EDB(AAS),
∴BC=DB;
第11题图
(2)若BD=8cm,求AC的长.
(2)解:由(1)得AC=BE,BC=BD,
∵E是BC的中点,BD=8cm,
∴AC=BE=BC=BD=4cm.
第11题图
解答题
12.如图,在四边形ABCD中,AB=BC,∠ABC=∠D=90°,BE⊥AD,垂足为E.试说明:BE=DE.
第12题图
在△BAE和△CBF中,,
∴△BAE≌△CBF(AAS),
∴BE=CF=DE,即BE=DE.
证明:如图,过点C作CF⊥BE,垂足为F,
∵BE⊥AD,CF⊥BE,∠ABC=∠D=90°,
∴∠FED=∠D=∠CFE=90°,∠AEB=∠BFC=90°,
∴四边形EDCF是矩形,∴DE=CF,
∵∠CBF+∠ABE=∠A+∠ABE=90°,
∴∠A=∠CBF,
谢 谢 观 看
第5课时 三角形全等的判定(4)
第十二章 全等三角形
一、选择题
1.如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD≌△AOP的依据是( D )
A.SSS B.ASA C.SSA D.HL
第1题图
D
2.下列条件中,不能判定两个直角三角形全等的是( C )
A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
C
二、填空题
3.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= 40° .
第3题图
40°
第4题图
4.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的依据是 AAS .(用字母表示)
AAS
5.如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,则还需要添加条件 AB=AC .
第5题图
AB=AC
三、解答题
6.如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
第6题图
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在Rt△ABF和Rt△DCE中,,
∴Rt△ABF≌Rt△DCE(HL).
7.如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,
求证:AF=CE.
第7题图
证明:∵DE=BF,
∴DE+EF=BF+EF,
即DF=BE,
在Rt△ADF和Rt△CBE中,
,
∴Rt△ADF≌Rt△CBE(HL),
∴AF=CE.
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.试说明:BE=CF.
第8题图
证明:∵AD平分∠BAC,
DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,
∠AED=∠AFD=90°,
∵AD=AD,
∴△AED≌△AFD(AAS),
∴DE=DF,
∵BD=CD,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
一、填空题
9.如图,CA⊥AB,垂足为点A,AB=8cm,AC=4cm,射线BM⊥AB,垂足为点B,一动点E从点A出发以2cm/s的速度沿射线AN运动,点D为射线BM上一动点,随着点E的运动而运动,且始终保持ED=CB,当点E运动 0或2或6或8 s时,△DEB与△BCA全等.
第9题图
0或2或6或8
二、解答题
10.如图,Rt△ABC的直角顶点C置于直线l上,AC=BC,现过A、B两点分别作直线l的垂线,垂足分别为点D、E.
(1)求证:△ACD≌△CBE;
第10题图
(1)证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠ACD=∠CBE=90°-∠ECB,
在△ACD与△CBE中,
,
∴△ACD≌△CBE(AAS);
(2)若BE=3,DE=5,求AD的长.
(2)解:由(1)可知△ACD≌△CBE,
∴CD=BE=3,AD=CE,
∵CE=CD+DE=8,
∴AD=8.
第10题图
解答题
11.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过点B、C向过点A的直线作垂线,垂足分别为E、F.
(1)如图1,当过点A的直线与斜边BC不相交时,求证:EF=BE+CF;
第11题图1
(1)证明:∵BE⊥EA,CF⊥AF,
∴∠BEA=∠AFC=90°,
∴∠ABE+∠EAB=90°,
∵∠BAC=90°,∴∠EAB+∠CAF=90°,
∴∠CAF=∠ABE,
在△ABE和△CAF中,,
∴△ABE≌△CAF(AAS),
∴EA=FC,BE=AF,
∴EF=AF+EA=BE+CF;
第11题图1
(2)如图2,当过点A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求EF的长.
第11题图2
(2)解:∵BE⊥EA,CF⊥AF,
∴∠BEA=∠AFC=90°,
∴∠ABE+∠EAB=90°,
∵∠BAC=90°,∴∠EAB+∠CAF=90°,
∴∠CAF=∠ABE,
在△ABE和△CAF中,,
∴△ABE≌△CAF(AAS),
∴EA=FC=3,AF=BE=10,
∴EF=AF-EA=7.
谢 谢 观 看
第6课时 专题全等三角形
第十二章 全等三角形
一、选择题
1.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( C )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
第1题图
C
2.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( A )
A.ASA B.AAS C.SAS D.SSS
第2题图
A
第3题图
3.如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中可以判断△ABC≌△DFE的依据是( B )
A.SAS B.AAS C.HL D.SSS
B
二、填空题
4.如图,AB=AC,若使△ABE≌△ACF,则还需要添加的条件是 ∠B=∠C(答案不唯一) .(写出一个即可)
第4题图
∠B=∠C(答案
不唯一)
第5题图
5.如图,AB⊥CD,CE⊥AD于点E,BF⊥AD于点F.若AB=CD,CE=8,BF=6,AD=10,则EF的长为 4 .
4
三、解答题
6.如图,点D,B在AE上,AC=DF,AD=BE,BC=EF.求证:
(1)△ABC≌△DEF;
证明:(1)∵AD=BE,
∴AD+DB=BE+DB,
即AB=DE,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS);
第6题图
(2)AC∥DF.
证明:(2)∵△ABC≌△DEF,
∴∠A=∠EDF,
∴AC∥DF.
第6题图
7.如图,有两个长度相等的滑梯BC与EF,滑梯BC的高AC与滑梯EF水平方向的长度DF相等,问两个滑梯的倾斜角∠B与∠F有什么数量关系?请说明理由.
第7题图
解:∠B与∠F互余,理由如下:
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠B=∠DEF,
∵∠DEF+∠F=90°,
∴∠B+∠F=90°,
即两个滑梯的倾斜角∠B与∠F互余.
一、填空题
8.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q分别是线段AC和射线AX上的动点,且AB=PQ,当AP= 10或20 时,△APQ与△ABC全等.
第8题图
10或20
二、解答题
9.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,与AC交于点G.
(1)求证:EF=BC;
(1)证明:∵线段AC绕点A旋转到AF的位置,
∴AC=AF,
∵∠CAF=∠BAE,
∴∠CAF+∠CAE=∠BAE+∠CAE,
∴∠EAF=∠BAC,
在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴EF=BC;
第9题图
(2)若∠B=65°,∠C=28°,求∠FGC的度数.
(2)解:∵AE=AB,∴∠AEB=∠B=65°,
∵△ABC≌△AEF,
∴∠AEF=∠B=65°,
∴∠FEC=180°-∠AEB-∠AEF=50°,
∵∠FGC是△EGC的外角,∠C=28°,
∴∠FGC=∠FEC+∠C=78°.
第9题图
解答题
10.如图,P为∠ABC的平分线上一点,点D和点E分别在AB和BC上,且PD=PE,试探究∠BDP与∠BEP之间的数量关系,并说明理由.
第10题图
解:∠BDP+∠BEP=180°,理由如下:
如图,过点P作PM⊥AB于点M,PN⊥BC于点N,
在△BPM和△BPN中,
,
∴△BPM≌△BPN(AAS),
∴PM=PN,
在Rt△DPM和Rt△EPN中,
,
∴Rt△DPM≌Rt△EPN(HL),
∴∠ADP=∠BEP,
∵∠BDP+∠ADP=180°,
∴∠BDP+∠BEP=180°.
谢 谢 观 看
第7课时 角的平分线的性质(1)
第十二章 全等三角形
一、选择题
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ长度的最小值为( B )
A.1 B.2 C.3 D.4
第1题图
B
2.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D,如果AC=3cm,那么AE+DE=( B )
A.2cm B.3cm C.4cm D.5cm
第2题图
B
3.如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( D )
A.100° B.110° C.120° D.130°
第3题图
D
二、填空题
4.如图,在△ABC中,∠A=70°,根据作图痕迹推断∠BOC的度数为 125 °.
第4题图
125
5.如图,在△ABC中,∠B=90°,AC=10,AD为此三角形的一条角平分线,若BD=3,则△ADC的面积为 15 .
第5题图
6.△ABC的周长为6,∠A和∠B的平分线相交于点P,若点P到边AB的距离为1,则△ABC的面积为 3 .
15
3
三、解答题
7.如图,已知在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD∶DC=2∶1,BC=7.8cm,求点D到AB的距离.
第7题图
解:如图,过点D作DE⊥AB于点E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE,
∵BD∶DC=2∶1,BC=7.8cm,
∴DC=BC=2.6cm,
∴DE=DC=2.6cm,
∴点D到AB的距离为2.6cm.
8.如图,△ABC的外角平分线BD、CE相交于点P,若点P到AC的距离为2,求点P到AB的距离.
第8题图
解:如图,作PF⊥AC,交AC的延长线于点F,作PG⊥BC于点G,作PH⊥AB,交AB的延长线于点H,
∵BD,CE是△ABC的外角平分线,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∵点P到AC的距离为2,即PF=2,
∴PH=2,
即点P到AB的距离为2.
9.如图,已知OD平分∠AOB,P是OD上一点,在OA,OB上取OA=OB,PM⊥BD于点M,PN⊥AD于点N,求证:PM=PN.
第9题图
证明:∵OD平分∠AOB,
∴∠1=∠2,
在△OBD和△OAD中,
,
∴△OBD≌△OAD(SAS),
∴∠3=∠4,
∴DO平分∠ADB,
∵PM⊥BD,PN⊥AD,
∴PM=PN.
一、填空题
10.如图,△ABC中,E为AC的中点,AD平分∠BAC,BA∶CA=2∶3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是 10 .
第10题图
10
二、解答题
11.如图,AD∥BC,DB平分∠ADC,CE平分∠BCD交AB于点E,交BD于点O,连接ED.求证:点O到EB与ED的距离相等.
第11题图
证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠BDC=∠ADC,∠ECD=∠BCD,
∴∠ODC+∠OCD=(∠ADC+∠BCD)=90°,
∴∠DOC=∠BOC=∠EOB=∠EOD=90°,
在△COD和△COB中,,
∴△COD≌△COB(ASA),
∴OB=OD,
在△BOE和△DOE中,,
∴△BOE≌△DOE(SAS),
∴∠BEO=∠DEO,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.0
第11题图
解答题
12.如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD,交AD的延长线于F,且BC=DC.
(1)BE与DF是否相等?请说明理由;
解:(1)BE=DF,理由如下:
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CF=CE,∠CFD=∠CEB=90°,
在Rt△CDF和Rt△CBE中,
,
∴Rt△CDF≌Rt△CBE(HL),
∴BE=DF;
第12题图
(2)若AB=14,AD=6,求DF的长.
解:(2)在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AF=AE,
∵AB=AE+BE=AF+DF=14①,
AD=AF-DF=6②,
∴①-②得2DF=8,
∴DF=4.
第12题图
谢 谢 观 看
第8课时 角的平分线的性质(2)
第十二章 全等三角形
一、选择题
1.如图,已知∠B=∠D=90°,BC=CD,∠BAC=35°,则∠DAC=( B )
A.25° B.35° C.50° D.70°
第1题图
B
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( C )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
第2题图
C
二、填空题
3.如图,∠AOB=78°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= 3 °.
第3题图
39
第4题图
4.如图,在△ACB中,∠C=90°,BD平分∠ABC交AC于点D,若AB=12,CD=6,则S△ABD= 36 .
36
三、解答题
5.如图,求作一个点P,到已知△ABC三边的距离相等.(不写作法,保留作图痕迹)
第5题图
解:如图所示,点P即为所求.
6.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
第6题图
解:如图,作DF⊥CA,交CA的延长线于点F,
∵CD平分∠ACB,DE⊥BC,
∴DF=DE,
∵S△ABC=14,
∴S△BCD+S△ACD=14,
∴DE·10+DF·4=14,
即5DE+2DE=14,
∴DE=2.
7.如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
第7题图
证明:如图,过点D作DN⊥AC于点N,DM⊥AB于点M,
则S△DCE=DN·CE,
S△DBF=BF·DM,
∵S△DCE=S△DBF,
∴DN·CE=BF·DM,
∵CE=BF,∴DM=DN,
∴AD平分∠BAC.
一、选择题
8.如图,点O在△ABC内,且到三边的距离相等.若∠A=50°,则∠BOC=( A )
A.115° B.105° C.125° D.130°
第8题图
A
二、填空题
9.平面上有三条直线两两相交且不共点,那么平面上到此三条直线距离相等的点的个数是 4 .
4
三、解答题
10.如图,BP、CP分别是△ABC的外角∠CBD、∠BCE的平分线.求证:点P在∠BAC的平分线上.
第10题图
证明:如图,过点P作PM⊥AD于点M,作PN⊥BC于点N,作PG⊥AE于点G,
∵BP平分∠CBD,CP平分∠BCE,
∴PM=PN,PG=PN,
∴PM=PG,
∴点P在∠BAC的平分线上.
解答题
11.已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个直角三角板的直角顶点与点C重合,它的两条直角边分别与OA、OB相交于点D、E.
(1)如图1,当CD⊥OA于点D,CE⊥OB于点E时,求证:CD=CE;
第11题图1
(1)证明:∵OM平分∠AOB,CD⊥OA,CE⊥OB,
∴CD=CE;
(2)当直角三角板绕点C旋转到CD与OA不垂直时,在图2这种情况下,(1)中的结论是否还成立?若成立,请说明理由;若不成立,请写出你的猜想,不需说明理由.
第11题图2
(2)解:(1)中的结论仍然成立.理由如下:
如图,过点C分别作CK⊥OA于点K,CH⊥OB于点H,
∵OM平分∠AOB,CK⊥OA,CH⊥OB,
∴CK=CH,∠CKD=∠CHE=90°,
∵∠1与∠2都为旋转角,
∴∠1=∠2,
在△CKD与△CHE中,,
∴△CKD≌△CHE(ASA),
∴CD=CE.
谢 谢 观 看
第9课时 复习巩固
第十二章 全等三角形
一、选择题
1.如图,△AOC≌△BOD,点A与点B是对应点,则下列结论错误的是( C )
A.∠A=∠B B.AO=BO
C.AB=CD D.AC=BD
第1题图
2.在△ABC和△A'B'C'中,AB=A'B',∠A=∠A',若证△ABC≌△A'B'C'还要从下列条件中补选一个,错误的选法是( C )
A.∠B=∠B' B.∠C=∠C'
C.BC=B'C' D.AC=A'C'
C
C
3.如图,某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建立在△ABC的( A )
A.两个内角的平分线的交点处
B.两边上的高的交点处
C.两边上的中线的交点处
D.两边的垂直平分线的交点处
第3题图
A
二、填空题
4.如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需添加一个条件: DC=BC(答案不唯一) .
第4题图
DC=BC(答案不唯一)
第5题图
5.如图,已知△AOB≌△A'OB',∠B=30°,∠AOA'=52°,则∠A'CO= 82° .
82°
6.如图,△ABC中,AB=9,BC=7,AC=8,点O是△ABC的三个内角的平分线的交点,S△AOB、S△BOC、S△AOC分别表示△AOB、△BOC、△AOC的面积,则S△AOB∶S△BOC∶S△AOC= 9∶7∶8 .
第6题图
9∶7∶8
三、解答题
7.如图,点C,E,B,F在同一条直线上,AB=DE,AC=DF,BF=CE.
求证:AC∥DF.
第7题图
证明:∵CE=BF,
∴CE+BE=BF+BE,即BC=EF,
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,∴AC∥DF.
8.如图,在△ACB中,已知∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),求点B的坐标.
第8题图
解:如图,作AD⊥x轴于点D,BE⊥x轴于点E,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,
∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∵C(-2,0),A(-6,3),
∴OC=2,CE=AD=3,OD=6,
∴BE=CD=OD-OC=4,OE=CE-OC=1,
∴点B的坐标是(1,4).
一、填空题
9.如图,在△ABC中,AB=4,BC=6,BD是△ABC的角平分线,DE⊥AB于点E,AF⊥BC于点F,若DE=2,则AF的长为 .
第9题图
二、解答题
10.如图,已知△ABC中,AB=AC,BD、CE是△ABC的高,BD与CE相交于点O.
(1)求证:BD=CE;
(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(AAS),∴BD=CE;
第10题图
(2)若∠A=80°,求∠BOC的度数.
(2)解:∵∠A=80°,∠ADB=∠AEC=90°,
∴∠BOC=∠EOD=360°-80°-90°-90°=100°.
第10题图
解答题
11.如图,AD是△ABC的角平分线,点F、E分别在边AC、AB上,连接DE、DF,且∠AFD+∠B=180°.
(1)求证:BD=FD;
第11题图
证明:(1)如图1,作DM⊥AB于点M,DN⊥AC于点N,
则∠DMB=∠DNF=90°,
∵AD平分∠BAC,∴DM=DN,
∵∠AFD+∠B=∠AFD+∠DFN=180°,
∴∠B=∠DFN,
在△DMB和△DNF中,,
∴△DMB≌△DNF(AAS),
∴BD=FD;
图1
(2)当AF+FD=AE时,求证:∠AFD=2∠AED.
证明:(2)如图2,在AB上截取AG=AF,连接DG,
∵AD平分∠BAC,∴∠DAF=∠DAG,
在△ADF和△ADG中,,
∴△ADF≌△ADG(SAS),
∴∠AFD=∠AGD,FD=GD,
∵AF+FD=AE,∴AG+GD=AE,
∵AE=AG+GE,∴GD=GE,
∴∠GDE=∠GED,
第11题图
∵∠AGD=∠GED+∠GDE=2∠GED,
∴∠AFD=2∠AED.
谢 谢 观 看
第1课时 全等三角形
第十二章 全等三角形
一、选择题
1.下列图形中,与如图所示图形全等的是( D )
第1题图
A
B
C
D
D
2.如图,已知△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是( C )
A.6cm B.5cm
C.7cm D.无法确定
第2题图
3.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( C )
A.AC=CE B.∠BAC=∠ECD
C.∠ACB=∠ECD D.∠B=∠D
第3题图
C
C
4.如图所示的两个三角形全等,则∠α的度数是( C )
A.58° B.72° C.50° D.60°
第4题图
C
5.如图,已知△ABC≌△DEF,CD平分∠BCA,FD交BC于G,若∠A=28°,∠CGF=85°,则∠E的度数是( A )
A.38° B.36° C.34° D.32°
第5题图
A
二、填空题
6.若△ABC≌△A'B'C',∠A=60°,∠B=40°,则∠C'= 80° .
7.如图,若△ABC≌△DEF,则x= 20 .
第7题图
80°
20
三、解答题
8.如图,△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,写出其他对应边及对应角.
第8题图
解:∵△ABC≌△ADE,∠B与∠D是对应角,AB与AD是对应边,
∴AC=AE,BC=DE,∠C=∠E,∠BAC=∠DAE,
即AC和AE,BC和DE是对应边,
∠C和∠E,∠BAC和∠DAE是对应角.
9.如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若EB⊥AD,∠F=62°,求∠A的度数;
解:(1)∵EB⊥AD,∴∠EBD=90°,
∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,
∵∠F=62°,∴∠A=90°-∠F=28°;
第9题图
(2)若AD=9cm,BC=5cm,求AB的长.
解:(2)∵△ACF≌△DBE,∴CA=BD,
∴CA-CB=BD-BC,即AB=CD,
∵AD=9cm,BC=5cm,
∴AB+CD=4cm,
∴AB=2cm.
一、填空题
10.三个全等三角形按如图所示的方式摆放,则∠1+∠2+∠3的度数是 180° .
第10题图
180°
第11题图
11.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为 135° .
135°
二、解答题
12.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数;
解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=∠ABE-∠DBC=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
第12题图
(2)求△CDP与△BEP的周长和.
解:(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴C△CDP+C△BEP=DC+DP+PC+BP+PE+BE
=DC+DE+BC+BE=15.5.
第12题图
解答题
13.如图所示,已知A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)BD、DE、CE之间有怎样的数量关系?请说明理由;
解:(1)BD=DE+CE,
理由:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE;
第13题图
(2)请你猜想当△ABD满足什么条件时,BD∥CE?并证明你的猜想.
解:(2)当△ABD满足∠ADB=90°时,BD∥CE,
证明:∵△BAD≌△ACE,
∴∠E=∠ADB=90°,
∴∠BDE=180°-∠ADB=90°=∠E,
∴BD∥CE.
第13题图
谢 谢 观 看
第2课时 三角形全等的判定(1)
第十二章 全等三角形
一、选择题
1.如图,在△ABC中,AB=AC,BE=CE,则直接由“SSS”可以判定( C )
第1题图
A.△ABD≌△ACD B.△BDE≌△CDE
C.△ABE≌△ACE D.以上都不对
C
2.如图,AD=BC,AC=BD,AC与BD交于点E,则图中可以用“SSS”判定全等的三角形共有( C )
A.1对 B.2对 C.3对 D.4对
第2题图
C
二、填空题
3.如图,AB=DC,AC与DB相交于点O,要使△ABC≌△DCB,则应添加条件 AC=DB .(写出一个条件即可)
第3题图
AC=DB
4.“三月三,放风筝”,如图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH,小明是通过识别全等三角形的方法得到的结论,则小明用的识别方法是 SSS .(用字母表示)
第4题图
SSS
三、解答题
5.如图,C是AB的中点,AD=CE,CD=BE.试说明:△ACD≌△CBE.
第5题图
证明:∵C是AB的中点,
∴AC=CB,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SSS).
6.如图所示,已知点A,E,F,C在同一条直线上,AB=CD,BF=DE,AE=CF.
求证:△ABF≌△CDE.
第6题图
证明:∵AE=CF,∴AF=CE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SSS).
7.如图,点D,E分别在边AC,AB上,且BE=CD,连接BD,CE,且BD=CE.
求证:△EBC≌△DCB.
第7题图
证明:在△EBC与△DCB中,
,
∴△EBC≌△DCB(SSS).
8.如图,点A、B、C、D在一条直线上,AC=DB,AE=DF,BE=CF.
(1)求证:∠E=∠F;
证明:(1)∵AC=DB,∴AB=DC,
在△ABE和△DCF中,,
∴△ABE≌△DCF(SSS),
∴∠E=∠F;
第8题图
(2)求证:AE∥DF.
证明:(2)由(1)知△ABE≌△DCF,
∴∠A=∠D,
∴AE∥DF.
一、填空题
9.如图,AB=AC,BD=CD,∠BAC=50°,∠B=40°,则∠ADC= 115° .
第9题图
115°
二、解答题
10.如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC,求证:∠A=∠C,且点O在∠AEC的平分线上.
第10题图
证明:如图,连接OE,
在△AOE和△COE中,
,
∴△AOE≌△COE(SSS),
∴∠A=∠C,∠AEO=∠CEO,
∴OE平分∠AEC,
即点O在∠AEC的平分线上.
解答题
11.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证:∠ACB=∠AFB.
第11题图
证明:在△ABC和△DEB中,,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE,
∵∠AFB=∠ACB+∠DBE=2∠ACB,
∴∠ACB=∠AFB.
谢 谢 观 看
第3课时 三角形全等的判定(2)
第十二章 全等三角形
一、选择题
1.如图,AD,BC相交于点O,且AO=DO,BO=CO,则△ABO≌△DCO,理由是( B )
A.SSS B.SAS C.ASA D.AAS
第1题图
B
2.如图,已知OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC=( A )
A.95° B.120° C.50° D.105°
第2题图
A
二、填空题
3.如图所示,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,若能用“SAS”说明△ABC≌△DEF,则需要添加一个适当的条件是 AC=DF .
第3题图
AC=DF
第4题图
4.如图,要测量池塘AB的宽度,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘AB的宽为 25 m.
25
5.如图,已知AB=AC,AD=AE,∠BAC=∠DAE,∠BAD=22°,∠ACE=30°,则∠ADE= 52° .
第5题图
52°
三、解答题
6.如图,点B是线段AD上一点,BC∥DE,AB=ED,BC=DB,
求证:△ABC≌△EDB.
第6题图
证明:∵BC∥DE,∴∠ABC=∠D,
在△ABC和△EDB中,
,
∴△ABC≌△EDB(SAS).
7.如图,在△ABC中,点D、E分别在AB、AC上,AB=AC,BD=CE,BE与CD交于点O.求证:∠ABE=∠ACD.
第7题图
证明:∵AB=AC,BD=CE,
∴AD=AE,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD.
8.如图,点C在线段AB上,△ACM与△CBN都是等边三角形,AN与MB交于点P.
求证:AN=BM.
第8题图
证明:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°,
∴∠ACN=∠MCB,
在△ACN和△MCB中,,
∴△ACN≌△MCB(SAS),
∴AN=BM.
一、选择题
9.如图,在平面直角坐标系中,点A(2,0),B(0,4),若△BOC与△ABO全等,则点C的坐标不能为( A )
A.(0,-4) B.(-2,0)
C.(2,4) D.(-2,4)
第9题图
A
10.如图,在△ABC中,∠B=∠C,BD=CE,CD=BF,则∠EDF=( B )
A.90°-∠A B.90°-∠A
C.180°-2∠A D.45°-∠A
第10题图
B
二、解答题
11.将两个大小不同的等腰直角三角板按如图1所示放置,图2是由它抽象出的几何图形,点B、C、E在同一条直线上,连接DC.
(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(1)解:△ABE≌△ACD,证明如下:
∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
在△ABE与△ACD中,,
∴△ABE≌△ACD(SAS);
第11题图
(2)证明:DC⊥BE.
(2)证明:由(1)得∠ACD=∠ABE=45°,
∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
第11题图
解答题
12.在△ABC中,AD是BC边上的中线,AB=5cm,AD=3cm,求AC长度的取值范围.
解:如图,延长AD到点E,使得AD=DE,连接BE,
∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,
,
∴△BDE≌△CDA(SAS),∴BE=AC,
∵AD=3cm,DA=DE,
∴AE=6cm,
∵AB=5cm,
∴AE-AB<BE<AB+AE,
即1cm<BE<11cm,
∴1cm<AC<11cm.
谢 谢 观 看
第4课时 三角形全等的判定(3)
第十二章 全等三角形
一、选择题
1.如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,则△APD与△APE全等的依据是( B )
A.SAS B.AAS C.SSS D.ASA
第1题图
B
2.如图,AC=DF,∠1=∠2,如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是( A )
A.∠A=∠D B.AB=DE
C.∠A=∠E D.∠B=∠E
第2题图
3.在Rt△ABC与Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠B',AB=B'A',则下列结论正确的是( C )
A.AB=A'C' B.BC=B'C'
C.AC=B'C' D.∠A=∠A'
A
C
二、填空题
4.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,∠B=∠C,若AB=6,BE=4,则CD= 4 .
第4题图
4
第5题图
5.如图,在△ABC中,∠ABC=45°,F是高AD和高BE的交点,CD=4,则线段DF的长度为 4 .
4
三、解答题
6.如图,已知CE⊥AB于点E,BF⊥AC于点F,BF交CE于点D,且AB=AC,求证:△ABF≌△ACE.
第6题图
证明:∵CE⊥AB,BF⊥AC,
∴∠AFB=∠AEC=90°,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(AAS).
7.如图,在△ABC中,∠B=∠C=∠EDF=50°,DE=DF,BE=5,CF=2,
求BC的长.
第7题图
解:∵∠B=∠C=∠EDF=50°,∠EDC=∠EDF+∠FDC=∠B+∠DEB,
∴∠FDC=∠DEB,
∵DE=FD,
∴△BED≌△CDF(AAS),
∴BD=CF=2,BE=CD=5,
∴BC=BD+CD=7.
8.如图,在△ABC中,E是AC的中点,点F在AB上,CD∥AB,交FE的延长线于点D.
(1)求证:EF=ED;
(1)证明:∵CD∥AB,∴∠A=∠ECD,
∵E是AC的中点,∴AE=CE,
在△AEF和△CED中,,
∴△AEF≌△CED(ASA),
∴EF=ED;
第8题图
(2)若AB=8,CD=6,求BF的长.
(2)解:由(1)知,△AEF≌△CED,∴AF=CD=6,
∴BF=AB-AF=2.
第8题图
一、选择题
9.如图,在平面直角坐标系中,点A的坐标为(2,3),且AO=BO,∠AOB=90°,则点B的坐标为( B )
A.(2,3) B.(-3,2)
C.(-3,-2) D.(-2,3)
第9题图
B
二、填空题
10.如图,点D,E在△ABC的BC边上,∠BAD=∠CAE,要推理得出△ABE≌△ACD,可以补充的一个条件是 AB=AC(答案不唯一) .(不添加辅助线,写出一个即可)
第10题图
AB=AC(答案不唯一)
三、解答题
11.如图,在△ABC与△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB于点F,AB=DE.
(1)求证:BC=DB;
第11题图
(1)证明:∵DE⊥AB,
∴∠BFE=90°,
∴∠ABC+∠DEB=90°,
∵∠ACB=90°,
∴∠ABC+∠A=90°,
∴∠A=∠DEB,
在△ABC和△EDB中,,
∴△ABC≌△EDB(AAS),
∴BC=DB;
第11题图
(2)若BD=8cm,求AC的长.
(2)解:由(1)得AC=BE,BC=BD,
∵E是BC的中点,BD=8cm,
∴AC=BE=BC=BD=4cm.
第11题图
解答题
12.如图,在四边形ABCD中,AB=BC,∠ABC=∠D=90°,BE⊥AD,垂足为E.试说明:BE=DE.
第12题图
在△BAE和△CBF中,,
∴△BAE≌△CBF(AAS),
∴BE=CF=DE,即BE=DE.
证明:如图,过点C作CF⊥BE,垂足为F,
∵BE⊥AD,CF⊥BE,∠ABC=∠D=90°,
∴∠FED=∠D=∠CFE=90°,∠AEB=∠BFC=90°,
∴四边形EDCF是矩形,∴DE=CF,
∵∠CBF+∠ABE=∠A+∠ABE=90°,
∴∠A=∠CBF,
谢 谢 观 看
第5课时 三角形全等的判定(4)
第十二章 全等三角形
一、选择题
1.如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD≌△AOP的依据是( D )
A.SSS B.ASA C.SSA D.HL
第1题图
D
2.下列条件中,不能判定两个直角三角形全等的是( C )
A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
C
二、填空题
3.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= 40° .
第3题图
40°
第4题图
4.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的依据是 AAS .(用字母表示)
AAS
5.如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,则还需要添加条件 AB=AC .
第5题图
AB=AC
三、解答题
6.如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
第6题图
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在Rt△ABF和Rt△DCE中,,
∴Rt△ABF≌Rt△DCE(HL).
7.如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,
求证:AF=CE.
第7题图
证明:∵DE=BF,
∴DE+EF=BF+EF,
即DF=BE,
在Rt△ADF和Rt△CBE中,
,
∴Rt△ADF≌Rt△CBE(HL),
∴AF=CE.
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E、F,且BD=CD.试说明:BE=CF.
第8题图
证明:∵AD平分∠BAC,
DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,
∠AED=∠AFD=90°,
∵AD=AD,
∴△AED≌△AFD(AAS),
∴DE=DF,
∵BD=CD,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
一、填空题
9.如图,CA⊥AB,垂足为点A,AB=8cm,AC=4cm,射线BM⊥AB,垂足为点B,一动点E从点A出发以2cm/s的速度沿射线AN运动,点D为射线BM上一动点,随着点E的运动而运动,且始终保持ED=CB,当点E运动 0或2或6或8 s时,△DEB与△BCA全等.
第9题图
0或2或6或8
二、解答题
10.如图,Rt△ABC的直角顶点C置于直线l上,AC=BC,现过A、B两点分别作直线l的垂线,垂足分别为点D、E.
(1)求证:△ACD≌△CBE;
第10题图
(1)证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠ACD=∠CBE=90°-∠ECB,
在△ACD与△CBE中,
,
∴△ACD≌△CBE(AAS);
(2)若BE=3,DE=5,求AD的长.
(2)解:由(1)可知△ACD≌△CBE,
∴CD=BE=3,AD=CE,
∵CE=CD+DE=8,
∴AD=8.
第10题图
解答题
11.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过点B、C向过点A的直线作垂线,垂足分别为E、F.
(1)如图1,当过点A的直线与斜边BC不相交时,求证:EF=BE+CF;
第11题图1
(1)证明:∵BE⊥EA,CF⊥AF,
∴∠BEA=∠AFC=90°,
∴∠ABE+∠EAB=90°,
∵∠BAC=90°,∴∠EAB+∠CAF=90°,
∴∠CAF=∠ABE,
在△ABE和△CAF中,,
∴△ABE≌△CAF(AAS),
∴EA=FC,BE=AF,
∴EF=AF+EA=BE+CF;
第11题图1
(2)如图2,当过点A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求EF的长.
第11题图2
(2)解:∵BE⊥EA,CF⊥AF,
∴∠BEA=∠AFC=90°,
∴∠ABE+∠EAB=90°,
∵∠BAC=90°,∴∠EAB+∠CAF=90°,
∴∠CAF=∠ABE,
在△ABE和△CAF中,,
∴△ABE≌△CAF(AAS),
∴EA=FC=3,AF=BE=10,
∴EF=AF-EA=7.
谢 谢 观 看
第6课时 专题全等三角形
第十二章 全等三角形
一、选择题
1.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( C )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°
第1题图
C
2.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( A )
A.ASA B.AAS C.SAS D.SSS
第2题图
A
第3题图
3.如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中可以判断△ABC≌△DFE的依据是( B )
A.SAS B.AAS C.HL D.SSS
B
二、填空题
4.如图,AB=AC,若使△ABE≌△ACF,则还需要添加的条件是 ∠B=∠C(答案不唯一) .(写出一个即可)
第4题图
∠B=∠C(答案
不唯一)
第5题图
5.如图,AB⊥CD,CE⊥AD于点E,BF⊥AD于点F.若AB=CD,CE=8,BF=6,AD=10,则EF的长为 4 .
4
三、解答题
6.如图,点D,B在AE上,AC=DF,AD=BE,BC=EF.求证:
(1)△ABC≌△DEF;
证明:(1)∵AD=BE,
∴AD+DB=BE+DB,
即AB=DE,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SSS);
第6题图
(2)AC∥DF.
证明:(2)∵△ABC≌△DEF,
∴∠A=∠EDF,
∴AC∥DF.
第6题图
7.如图,有两个长度相等的滑梯BC与EF,滑梯BC的高AC与滑梯EF水平方向的长度DF相等,问两个滑梯的倾斜角∠B与∠F有什么数量关系?请说明理由.
第7题图
解:∠B与∠F互余,理由如下:
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠B=∠DEF,
∵∠DEF+∠F=90°,
∴∠B+∠F=90°,
即两个滑梯的倾斜角∠B与∠F互余.
一、填空题
8.如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q分别是线段AC和射线AX上的动点,且AB=PQ,当AP= 10或20 时,△APQ与△ABC全等.
第8题图
10或20
二、解答题
9.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,与AC交于点G.
(1)求证:EF=BC;
(1)证明:∵线段AC绕点A旋转到AF的位置,
∴AC=AF,
∵∠CAF=∠BAE,
∴∠CAF+∠CAE=∠BAE+∠CAE,
∴∠EAF=∠BAC,
在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴EF=BC;
第9题图
(2)若∠B=65°,∠C=28°,求∠FGC的度数.
(2)解:∵AE=AB,∴∠AEB=∠B=65°,
∵△ABC≌△AEF,
∴∠AEF=∠B=65°,
∴∠FEC=180°-∠AEB-∠AEF=50°,
∵∠FGC是△EGC的外角,∠C=28°,
∴∠FGC=∠FEC+∠C=78°.
第9题图
解答题
10.如图,P为∠ABC的平分线上一点,点D和点E分别在AB和BC上,且PD=PE,试探究∠BDP与∠BEP之间的数量关系,并说明理由.
第10题图
解:∠BDP+∠BEP=180°,理由如下:
如图,过点P作PM⊥AB于点M,PN⊥BC于点N,
在△BPM和△BPN中,
,
∴△BPM≌△BPN(AAS),
∴PM=PN,
在Rt△DPM和Rt△EPN中,
,
∴Rt△DPM≌Rt△EPN(HL),
∴∠ADP=∠BEP,
∵∠BDP+∠ADP=180°,
∴∠BDP+∠BEP=180°.
谢 谢 观 看
第7课时 角的平分线的性质(1)
第十二章 全等三角形
一、选择题
1.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ长度的最小值为( B )
A.1 B.2 C.3 D.4
第1题图
B
2.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D,如果AC=3cm,那么AE+DE=( B )
A.2cm B.3cm C.4cm D.5cm
第2题图
B
3.如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( D )
A.100° B.110° C.120° D.130°
第3题图
D
二、填空题
4.如图,在△ABC中,∠A=70°,根据作图痕迹推断∠BOC的度数为 125 °.
第4题图
125
5.如图,在△ABC中,∠B=90°,AC=10,AD为此三角形的一条角平分线,若BD=3,则△ADC的面积为 15 .
第5题图
6.△ABC的周长为6,∠A和∠B的平分线相交于点P,若点P到边AB的距离为1,则△ABC的面积为 3 .
15
3
三、解答题
7.如图,已知在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD∶DC=2∶1,BC=7.8cm,求点D到AB的距离.
第7题图
解:如图,过点D作DE⊥AB于点E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE,
∵BD∶DC=2∶1,BC=7.8cm,
∴DC=BC=2.6cm,
∴DE=DC=2.6cm,
∴点D到AB的距离为2.6cm.
8.如图,△ABC的外角平分线BD、CE相交于点P,若点P到AC的距离为2,求点P到AB的距离.
第8题图
解:如图,作PF⊥AC,交AC的延长线于点F,作PG⊥BC于点G,作PH⊥AB,交AB的延长线于点H,
∵BD,CE是△ABC的外角平分线,
∴PF=PG,PG=PH,
∴PF=PG=PH,
∵点P到AC的距离为2,即PF=2,
∴PH=2,
即点P到AB的距离为2.
9.如图,已知OD平分∠AOB,P是OD上一点,在OA,OB上取OA=OB,PM⊥BD于点M,PN⊥AD于点N,求证:PM=PN.
第9题图
证明:∵OD平分∠AOB,
∴∠1=∠2,
在△OBD和△OAD中,
,
∴△OBD≌△OAD(SAS),
∴∠3=∠4,
∴DO平分∠ADB,
∵PM⊥BD,PN⊥AD,
∴PM=PN.
一、填空题
10.如图,△ABC中,E为AC的中点,AD平分∠BAC,BA∶CA=2∶3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是 10 .
第10题图
10
二、解答题
11.如图,AD∥BC,DB平分∠ADC,CE平分∠BCD交AB于点E,交BD于点O,连接ED.求证:点O到EB与ED的距离相等.
第11题图
证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠BDC=∠ADC,∠ECD=∠BCD,
∴∠ODC+∠OCD=(∠ADC+∠BCD)=90°,
∴∠DOC=∠BOC=∠EOB=∠EOD=90°,
在△COD和△COB中,,
∴△COD≌△COB(ASA),
∴OB=OD,
在△BOE和△DOE中,,
∴△BOE≌△DOE(SAS),
∴∠BEO=∠DEO,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.0
第11题图
解答题
12.如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD,交AD的延长线于F,且BC=DC.
(1)BE与DF是否相等?请说明理由;
解:(1)BE=DF,理由如下:
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CF=CE,∠CFD=∠CEB=90°,
在Rt△CDF和Rt△CBE中,
,
∴Rt△CDF≌Rt△CBE(HL),
∴BE=DF;
第12题图
(2)若AB=14,AD=6,求DF的长.
解:(2)在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AF=AE,
∵AB=AE+BE=AF+DF=14①,
AD=AF-DF=6②,
∴①-②得2DF=8,
∴DF=4.
第12题图
谢 谢 观 看
第8课时 角的平分线的性质(2)
第十二章 全等三角形
一、选择题
1.如图,已知∠B=∠D=90°,BC=CD,∠BAC=35°,则∠DAC=( B )
A.25° B.35° C.50° D.70°
第1题图
B
2.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( C )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
第2题图
C
二、填空题
3.如图,∠AOB=78°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= 3 °.
第3题图
39
第4题图
4.如图,在△ACB中,∠C=90°,BD平分∠ABC交AC于点D,若AB=12,CD=6,则S△ABD= 36 .
36
三、解答题
5.如图,求作一个点P,到已知△ABC三边的距离相等.(不写作法,保留作图痕迹)
第5题图
解:如图所示,点P即为所求.
6.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
第6题图
解:如图,作DF⊥CA,交CA的延长线于点F,
∵CD平分∠ACB,DE⊥BC,
∴DF=DE,
∵S△ABC=14,
∴S△BCD+S△ACD=14,
∴DE·10+DF·4=14,
即5DE+2DE=14,
∴DE=2.
7.如图,CE=BF,且S△DCE=S△DBF,求证:AD平分∠BAC.
第7题图
证明:如图,过点D作DN⊥AC于点N,DM⊥AB于点M,
则S△DCE=DN·CE,
S△DBF=BF·DM,
∵S△DCE=S△DBF,
∴DN·CE=BF·DM,
∵CE=BF,∴DM=DN,
∴AD平分∠BAC.
一、选择题
8.如图,点O在△ABC内,且到三边的距离相等.若∠A=50°,则∠BOC=( A )
A.115° B.105° C.125° D.130°
第8题图
A
二、填空题
9.平面上有三条直线两两相交且不共点,那么平面上到此三条直线距离相等的点的个数是 4 .
4
三、解答题
10.如图,BP、CP分别是△ABC的外角∠CBD、∠BCE的平分线.求证:点P在∠BAC的平分线上.
第10题图
证明:如图,过点P作PM⊥AD于点M,作PN⊥BC于点N,作PG⊥AE于点G,
∵BP平分∠CBD,CP平分∠BCE,
∴PM=PN,PG=PN,
∴PM=PG,
∴点P在∠BAC的平分线上.
解答题
11.已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个直角三角板的直角顶点与点C重合,它的两条直角边分别与OA、OB相交于点D、E.
(1)如图1,当CD⊥OA于点D,CE⊥OB于点E时,求证:CD=CE;
第11题图1
(1)证明:∵OM平分∠AOB,CD⊥OA,CE⊥OB,
∴CD=CE;
(2)当直角三角板绕点C旋转到CD与OA不垂直时,在图2这种情况下,(1)中的结论是否还成立?若成立,请说明理由;若不成立,请写出你的猜想,不需说明理由.
第11题图2
(2)解:(1)中的结论仍然成立.理由如下:
如图,过点C分别作CK⊥OA于点K,CH⊥OB于点H,
∵OM平分∠AOB,CK⊥OA,CH⊥OB,
∴CK=CH,∠CKD=∠CHE=90°,
∵∠1与∠2都为旋转角,
∴∠1=∠2,
在△CKD与△CHE中,,
∴△CKD≌△CHE(ASA),
∴CD=CE.
谢 谢 观 看
第9课时 复习巩固
第十二章 全等三角形
一、选择题
1.如图,△AOC≌△BOD,点A与点B是对应点,则下列结论错误的是( C )
A.∠A=∠B B.AO=BO
C.AB=CD D.AC=BD
第1题图
2.在△ABC和△A'B'C'中,AB=A'B',∠A=∠A',若证△ABC≌△A'B'C'还要从下列条件中补选一个,错误的选法是( C )
A.∠B=∠B' B.∠C=∠C'
C.BC=B'C' D.AC=A'C'
C
C
3.如图,某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建立在△ABC的( A )
A.两个内角的平分线的交点处
B.两边上的高的交点处
C.两边上的中线的交点处
D.两边的垂直平分线的交点处
第3题图
A
二、填空题
4.如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需添加一个条件: DC=BC(答案不唯一) .
第4题图
DC=BC(答案不唯一)
第5题图
5.如图,已知△AOB≌△A'OB',∠B=30°,∠AOA'=52°,则∠A'CO= 82° .
82°
6.如图,△ABC中,AB=9,BC=7,AC=8,点O是△ABC的三个内角的平分线的交点,S△AOB、S△BOC、S△AOC分别表示△AOB、△BOC、△AOC的面积,则S△AOB∶S△BOC∶S△AOC= 9∶7∶8 .
第6题图
9∶7∶8
三、解答题
7.如图,点C,E,B,F在同一条直线上,AB=DE,AC=DF,BF=CE.
求证:AC∥DF.
第7题图
证明:∵CE=BF,
∴CE+BE=BF+BE,即BC=EF,
又∵AB=DE,AC=DF,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE,∴AC∥DF.
8.如图,在△ACB中,已知∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),求点B的坐标.
第8题图
解:如图,作AD⊥x轴于点D,BE⊥x轴于点E,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠CAD=90°,
∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∵C(-2,0),A(-6,3),
∴OC=2,CE=AD=3,OD=6,
∴BE=CD=OD-OC=4,OE=CE-OC=1,
∴点B的坐标是(1,4).
一、填空题
9.如图,在△ABC中,AB=4,BC=6,BD是△ABC的角平分线,DE⊥AB于点E,AF⊥BC于点F,若DE=2,则AF的长为 .
第9题图
二、解答题
10.如图,已知△ABC中,AB=AC,BD、CE是△ABC的高,BD与CE相交于点O.
(1)求证:BD=CE;
(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(AAS),∴BD=CE;
第10题图
(2)若∠A=80°,求∠BOC的度数.
(2)解:∵∠A=80°,∠ADB=∠AEC=90°,
∴∠BOC=∠EOD=360°-80°-90°-90°=100°.
第10题图
解答题
11.如图,AD是△ABC的角平分线,点F、E分别在边AC、AB上,连接DE、DF,且∠AFD+∠B=180°.
(1)求证:BD=FD;
第11题图
证明:(1)如图1,作DM⊥AB于点M,DN⊥AC于点N,
则∠DMB=∠DNF=90°,
∵AD平分∠BAC,∴DM=DN,
∵∠AFD+∠B=∠AFD+∠DFN=180°,
∴∠B=∠DFN,
在△DMB和△DNF中,,
∴△DMB≌△DNF(AAS),
∴BD=FD;
图1
(2)当AF+FD=AE时,求证:∠AFD=2∠AED.
证明:(2)如图2,在AB上截取AG=AF,连接DG,
∵AD平分∠BAC,∴∠DAF=∠DAG,
在△ADF和△ADG中,,
∴△ADF≌△ADG(SAS),
∴∠AFD=∠AGD,FD=GD,
∵AF+FD=AE,∴AG+GD=AE,
∵AE=AG+GE,∴GD=GE,
∴∠GDE=∠GED,
第11题图
∵∠AGD=∠GED+∠GDE=2∠GED,
∴∠AFD=2∠AED.
谢 谢 观 看
