第十四章 整式的乘法与因式分解 习题课件(共266张PPT) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 第十四章 整式的乘法与因式分解 习题课件(共266张PPT) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 10:25:59 | ||
图片预览


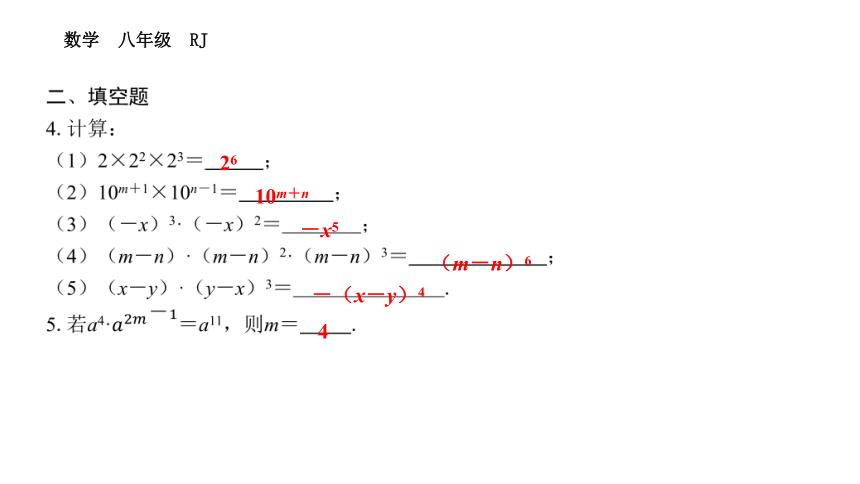








文档简介
(共266张PPT)
第1课时 同底数幂的乘法
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算:a5·a6=( A )
A.a11 B.a12 C.a30 D.a31
(2)下列计算正确的是( D )
A.x3·x3=2x3 B.x·x3=x3
C.x3·x2=x6 D.x3·x4=x7
(3)下列计算正确的是( D )
A.b3·b2=b6 B.x3+x3=x6
C.a4+a2=a6 D.m·m5=m6
A
D
D
2.计算-(-m2)·(-m)3·(-m)的正确结果是( C )
A.-m3 B.m5 C.m6 D.-m6
3.(1)已知2m=1,2n=3,则2m+n=( B )
A.2 B.3 C.4 D.6
(2)已知x+y-3=0,则2x·2y的值为( B )
A.64 B.8 C.6 D.12
C
B
B
二、填空题
4.计算:
(1)2×22×23= 26 ;
(2)10m+1×10n-1= 10m+n ;
(3)(-x)3·(-x)2= -x5 ;
(4)(m-n)·(m-n)2·(m-n)3= (m-n)6 ;
(5)(x-y)·(y-x)3= -(x-y)4 .
5.若a4·=a11,则m= 4 .
26
10m+n
-x5
(m-n)6
-(x-y)4
4
三、解答题
6.计算:
(1)(-x)(-x3)(-x3)(-x4);
解:原式=x4·x7
=x11.
(2)(-a2)·(-a)3;
解:原式=(-a2)·(-a3)
=a2+3
=a5.
(3)(x-2y)2(x-2y)3.
解:原式=(x-2y)2+3
=(x-2y)5.
7.计算下列各题:
(1)(a-b)3·(a-b)2·(b-a)5;
解:原式=(a-b)5·[-(a-b)5]
=-(a-b)10.
(2)a2·a3-(-a3)·a4+a6·(-a);
解:原式=a5+a7-a7
=a5.
(3)(m-n)2(n-m)3(m-n)6.
解:原式=(n-m)2(n-m)3(n-m)6
=(n-m)2+3+6
=(n-m)11.
8.(1)若ax+3=a2x+1(a≠0,a≠1),求x的值;
解:由题意得x+3=2x+1,
则x=2.
(2)若px·p6=p2x(p≠0,p≠1),求x的值;
解:由题意得px+6=p2x,
∴x+6=2x,则x=6.
(3)若an+1·am+n=a6(a≠0且a≠1),且2m=8,求mn的值.
解:由题意得,an+1·am+n=am+2n+1=a6,
则m+2n=5,
∵2m=8=23,∴m=3,
∴3+2n=5,∴n=1,
故mn=3.
一、填空题
9.已知x·xm·xn=x14(x≠0,x≠1),且m比n大3,则mn的值为 40 .
10.已知10α=3,10β=5,10γ=7,试把105写成底数是10的幂的形式是 10α+β+γ .
40
10α+β+γ
二、解答题
11.(1)若2a+5=9,求3×2a+4的值;
解:∵2a+5=9,
∴2a+4×2=9,
∴2a+4=,
则3×2a+4=3×=.
(2)已知a+b+c=3,求22a-3·23b-2·2a+3c的值.
解:22a-3·23b-2·2a+3c
=22a-3+3b-2+a+3c
=23(a+b+c)-5,
∵a+b+c=3,
∴原式=23×3-5=24=16.
12.规定运算:a*b=2a×2b.
(1)求2*3的值;
解:(1)∵a*b=2a×2b,
(2)若2*(x+1)=16,求x的值.
∴2*3=22×23=4×8=32;
解:(2)∵2*(x+1)=16,
∴22·2x+1=24,即22+x+1=24,
∴2+x+1=4,
解得:x=1.
解答题
13.记M(1)=-2,
M(2)=(-2)×(-2),
M(3)=(-2)×(-2)×(-2),
…,
M(n)=.
(1)计算:M(5)+M(6);
(2)求2M(2023)+M(2024)的值;
(3)说明2M(n)与M(n+1)互为相反数.
解:(1)M(5)+M(6)
=(-2)5+(-2)6
=-32+64=32;
(2)2M(2023)+M(2024)
=2×(-2)2023+(-2)2024
=-22024+22024=0;
(3)2M(n)+M(n+1)
=2·(-2)n+(-2)n+1
=(-2)n(2-2)=0,
∴2M(n)与M(n+1)互为相反数.
谢 谢 观 看
第2课时 幂的乘方
第十四章 整式的乘法与因式分解
一、选择题
1.计算:(-a4)2=( C )
A.2 B.-4 C. D.-a8
2.下列各式运算正确的是( D )
A.a3+a3= B.x3·x2=x6
C.(a3)2= D.(-a2)3=-a6
3.下列各式运算正确的是( B )
A.(x4)3=x7 B.(am)2=a2m
C.[(-a)2]5=-a10 D.(-a3)2=-a6
C
D
B
4.下列计算结果是a9的是( A )
A.a3·a6 B.(a3)6
C.a3+a6 D.a9+a9
A
二、解答题
5.计算:
(1)(102)3; (2)-(a2)4;
解:原式=106;
解:原式=-a8.
(3)(x3)5·x3; (4)[(-x)2]3;
解:原式=x15·x3=x18;
解:原式=x6.
(5)(-a)2(a2)2;
解:原式=a6;
(6)x·(-x2)2-x2·x3.
解:原式=x5-x5
=0.
6.计算:
(1)x2·x5·x+4(-x4)2+(x2)4;
解:原式=x8+4x8+x8
=6x8.
(2)9(x3)2-x2·x4-(x2)3;
解:原式=9x6-x6-x6
=7x6.
(3)a3·a·a4+7(a4)2+(-a2)4;
解:原式=a8+7a8+a8
=9a8.
(4)(-a)3·a2-(-a)2·(-a3).
解:原式=-a5+a2·a3
=0.
7.解方程:
(1)23x-1·22-x=2x+2;
解:∵23x-1·22-x=2x+2,
∴3x-1+2-x=x+2,
解得x=1.
(2)3x·92x=910.
解:∵3x·92x=910,
∴3x·34x=320,
∴x+4x=20,
解得x=4.
一、选择题
8.若x,y均为正整数,且2x·4y=32,则x+2y的值为( C )
A.3 B.4 C.5 D.6
C
二、填空题
9.已知am=3,a2m+n=45,则an= 5 .
10.已知27b=9×3a+3,16=4×22b-2,则a+b的值为 3 .
5
3
三、解答题
11.已知n为正整数,且x2n=4,求9(x3n)2-13(x2)2n的值.
解:∵x2n=4,
∴9(x3n)2-13(x2)2n
=9(x2n)3-13(x2n)2
=9×43-13×42
=368.
12.解答下列问题:
(1)已知3m=5,3n=2,求33m+2n+1的值;
解:∵3m=5,3n=2,
∴原式=(3m)3·(3n)2×3
=53×22×3
=125×4×3
=1500.
(2)若3x+4y-3=0,求27x·81y的值;
解:∵3x+4y-3=0,
∴3x+4y=3,
∴原式=33x·34y
=33x+4y
=33
=27.
(3)已知16m=4×22n-2,27n=9×3m+3,求(m-n)2024的值.
解:∵16m=4×22n-2,27n=9×3m+3,
∴24m=22×22n-2,33n=32×3m+3,
则4m=2+2n-2,3n=2+m+3,
解得:m=1,n=2,
则(m-n)2024=1.
13.比较大小:
(1)比较2100与375的大小;
解:∵2100=(24)25=1625,
375=(33)25=2725,
而16<27,
∴1625<2725,
∴2100<375.
(2)比较344、433、522的大小;
解:∵344=(34)11=8111,
433=(43)11=6411,
522=(52)11=2511,
而81>64>25,
∴8111>6411>2511,
即344>433>522.
(3)已知a2=2,b3=3,比较a、b的大小.
解:由b3=3可得b>0,
当a<0时,a<b;
当a>0时,a6=8,b6=9,
∵8<9,
∴a6<b6,
∴a<b,
综上所述,a<b.
解答题
14.若2a=2,4b=6,8c=12,试求a,b,c的数量关系.
解:∵4b=6,∴22b=6,
∵8c=12,∴23c=12,
∴2a·22b=2×6=12,
即2a+2b=12,
∴2a+2b=23c,
∴a+2b=3c.
谢 谢 观 看
第3课时 积的乘方
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算的结果是( C )
A.6x6 B.8x27 C.8x9 D.6x
(2)计算的结果是( C )
A.m6n B.m5n2 C.m6n2 D.m3n2
(3)计算的结果是( B )
A.-m5n B.-m6n3
C.m6n3 D.-m5n3
C
C
B
2.(1)下列计算正确的是( C )
A.x2·x4=x8 B.=x5
C.x2+x2=2x2 D.(3x)2=3x2
(2)下列运算中,正确的是( A )
A.=16x4y6
B.-=12x2y6
C.=-9x9y
D.(-x)3·x2·(-x)=x5
C
A
3.(1)计算:2200×=( A )
A.1 B.-1 C.2400 D.-2400
(2)计算:(-4)2023×=( D )
A.4 B.-4 C. D.-
4.已知xa=2,xb=4,则x2a+b的值是( D )
A.2 B.6 C.8 D.16
A
D
D
二、填空题
5.若(a3·ax)2=a20,则x的值为 7 .
6.计算:·= - .
7.计算:(1)-= -x3y6 ;
(2)(-a3)4+(-2a2)3= a12-8a6 .
7
-
-x3y6
a12-8a6
三、解答题
8.计算:
(1)(-5b)3;
解:原式=-125b3.
(2)-;
解:原式=-a4b6.
(3).
解:原式=a4b2.
9.计算:
(1)(-a3b6)2-(-a2b4)3-2a4b2·(ab5)2;
解:原式=a6b12+a6b12-2a4b2·a2b10
=2a6b12-2a6b12
=0.
(2)a3·a·a4+(-2a4)2+(a2)4;
解:原式=a8+4a8+a8
=6a8.
(3)(2a2)3+(-3a3)2+(a2)2·a2;
解:原式=8a6+9a6+a4·a2
=8a6+9a6+a6
=18a6.
(4)m·m5+(-2m3)2-4(m2)3;
解:原式=m6+4m6-4m6
=m6.
(5)××.
解:原式=×××
=××
=-1××
=-.
一、填空题
10.(1)计算:×41010= ;
(2)计算:[a(a-b)2]3·[a2(b-a)3]2= a7(a-b)12 ;
(3)如果=a9b12,那么m+n= 7 ;
(4)已知an=-1,b2n=3,则(-a2b)4n的值为 9 ;
(5)已知3m·9m·27m·81m=330,则m的值为 3 .
11.有一个棱长10cm的正方体,在某种物质的作用下,棱长每秒扩大到之前的102倍,则3秒后该正方体的体积是 1021 cm3.
a7(a-b)12
7
9
3
1021
二、解答题
12.(1)已知2x+5y-3=0,求4x·32y的值;
解:∵2x+5y-3=0,
∴2x+5y=3,
则原式=(22)x·(25)y
=22x·25y
=22x+5y
=23
=8.
(2)已知25m·2·10n=57·24,求m,n的值.
解:25m·2·10n=52m·2·(2×5)n
=52m+n·2n+1,
∵25m·2·10n=57·24,
∴52m+n·2n+1=57·24,
则,解得,
∴m的值为2,n的值为3.
13.计算下列各题:
(1)0.1259×(-8)10+×(2)12;
解:原式=(0.125×8)9×8+×
=1×8+1×
=.
(2)an-5·(an+1b3m-2)2+(an-1bm-2)3·(-b3m+2).
解:原式=an-5·(a2n+2b6m-4)+(a3n-3b3m-6)·(-b3m+2)
=a3n-3b6m-4-a3n-3b6m-4
=0.
解答题
14.若am=an(a>0且a≠1,m、n是正整数),则m=n.
试利用上述结论分别求下列各方程中x的值:
(1)2×8x=27;
解:(1)原方程可化为2×23x=27,
∴23x+1=27,
∴3x+1=7,
解得x=2;
(2)2x+1×3x+1=36x-2;
解:(2)原方程可化为(2×3)x+1=36x-2,
∴6x+1=62(x-2),
∴x+1=2(x-2),
解得x=5;
(3)2x+2+2x+1=24.
解:(3)原方程可化为2×2x+1+2x+1=24,
∴3×2x+1=3×8,
∴2x+1=8=23,
∴x+1=3,
解得x=2.
谢 谢 观 看
第4课时 整式的乘法(1)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算6x2·x3的结果是( B )
A.6x B.6x5 C.6x6 D.6x9
(2)计算(2x)3·(-x2)的结果为( C )
A.8x6 B.-2x5 C.-8x5 D.2x5
(3)计算:(-2x2y3)·3xy2=( B )
A.-6x2y6 B.-6x3y5
C.-5x3y5 D.-24x7y5
B
C
B
2.下列运算正确的是( D )
A.4x+5y=9xy B.2a3·a3=8a6
C.a2·a3=a6 D.(-ab)4=a4b4
3.若( )·(-xy)2=4x2y3,则括号里应填的单项式是( A )
A.4y B.-4y C.4xy D.-2xy
D
A
二、填空题
4.计算:(1)(-2x2)·3x4= -6x6 ;
(2)-4a3b2c·3ab3= -12a4b5c ;
(3)(3×105)×(8×105)= 2.4×1011 .(结果用科学记数法表示)
5.计算:3xmy3·(-2xym+1)= -6xm+1ym+4 .(m是正整数)
6.(1)已知3x3y·★=12x5y,则“★”所表示的式子是 4x2 ;
(2)若5am+1b2与3an+2bn的积是15a8b4,则nm= 8 .
-6x6
-12a4b5c
2.4×1011
-6xm+1ym+4
4x2
8
三、解答题
7.计算:
(1)·;
解:原式=-×a3bc2
=-a3bc2.
(2)·(-3xy);
解:原式=4x4y2·(-3xy)
=-12x5y3.
(3)(5×105)×(3×102).
解:原式=1.5×108.
8.计算下列各题:
(1)2x7·(-x3)-(-x3)2·x4;
解:原式=-2x10-x6·x4
=-2x10-x10
=-3x10.
(2)(-2x2y)3+(3x)2·(-x)4·y3;
解:原式=-8x6y3+9x2·x4y3
=-8x6y3+9x6y3
=x6y3.
(3)(-3a3)2·a3+(-4a2)·a7-(5a3)3;
解:原式=9a6·a3-4a2·a7-125a9
=9a9-4a9-125a9
=-120a9.
(4)先化简,再求值:(-2a2b3)(-ab2)2+·4b,其中a=2,b=1.
解:原式=-2a2b3·a2b4+a4b6·4b
=-2a4b7+a4b7
=-a4b7,
当a=2,b=1时,
原式=-24×1=-16.
一、选择题
9.计算2x·(-3xy)2·(-x2y)3的结果是( C )
A.18x8y5 B.6x9y5
C.-18x9y5 D.-6x4y5
C
二、填空题
10.(1)若2a3y2·(-4a2y3)=ma5yn,则m+n的值为 -3 ;
(2)若-5am+1·b2n-1·2ab2=-10a4b4,则m-n的值为 ;
(3)如果单项式-3x2a-by2与x3a+by5a+8b是同类项,那么这两个单项式的积是 10y4 .
-3
-x10y4
三、解答题
11.成都市环保局将一个长为2×106分米,宽为4×104分米,高为8×102分米的长方体废水池中的满池废水注入正方体贮水池净化,那么请你想一想,能否恰好有一个正方体贮水池将这些废水刚好装满?若有,求出正方体贮水池的棱长;若没有,请说明理由.
解:有,
∵长方体废水池的容积为:
(2×106)×(4×104)×(8×102)
=64×1012
=43×(104)3
=(4×104)3立方分米,
∴正方体水池的棱长为4×104分米.
解答题
12.解答下列各题:
(1)已知(2x3y2)·(-3xmy3)·(5x2yn)=-30x4y2,求m+n的值;
解:∵(2x3y2)·(-3xmy3)·(5x2yn)
=-30xm+5yn+5=-30x4y2,
∴m+5=4,n+5=2,即m=-1,n=-3,
则m+n=-4.
(2)若[-3(x+y)m(x-y)2n]2·[-(x+y)2]=-9(x+y)10(x-y)10-n,
求(m-n)3的值;
解:∵[-3(x+y)m(x-y)2n]2·[-(x+y)2]
=-9(x+y)2m+2(x-y)4n
=-9(x+y)10(x-y)10-n,
∴2m+2=10,4n=10-n,
∴m=4,n=2,
当m=4,n=2时,
(m-n)3=×(4-2)3=2.
(3)已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的平方根.
解:(-2x3m+1y2n)·(7xn-6y-3-m)
=-14x(3m+1)+(n-6)y2n+(-3-m)
=-14x3m+n-5y2n-m-3,
∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴,解得,
∴m2+n=7,
∴m2+n的平方根是±.
谢 谢 观 看
第5课时 整式的乘法(2)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算:x(x2-1)=( B )
A.x3-1 B.x3-x
C.x3+x D.x2-x
(2)把2a(ab-b+c)化简后得( D )
A.2a2b-ab+ac B.2a2-2ab+2ac
C.2a2b+2ab+2ac D.2a2b-2ab+2ac
B
D
(3)化简:(-3s+t)·(-7st2)=( B )
A.21s2t2-14st3 B.21s2t2-st3
C.-21s2t2+14st3 D.-21s2t2+st
B
2.已知x2-4x-1=0,则代数式x(x-4)+1的值为( A )
A.2 B.1 C.0 D.-1
3.某同学在计算-3x2乘一个多项式时错误的计算成了加法,得到的答案是x2-x+1,由此可以推断正确的计算结果是( C )
A.4x2-x+1 B.x2-x+1
C.-12x4+3x3-3x2 D.无法确定
A
C
二、填空题
4.计算:xm·(2xm-4x2-8y)= 2x2m-4xm+2-8xmy .(m为正整数)
5.(1)若(x2-a)x+2x的展开式中只含有x3这一项,则a的值是 2 ;
(2)若3x(x+1)=mx2+nx,则m+n= 6 .
2x2m-4xm+2-8xmy
2
6
三、解答题
6.计算:
(1)2ab2·(3a2b-2ab-1);
解:原式=6a3b3-4a2b3-2ab2.
(2)-3x·.
解:原式=-x3y3-6xy2+3x.
7.计算:
(1)2x-3x;
解:原式=x2-2x-x2+5x
=3x.
(2)2x(-x2+3x-4)+3x2;
解:原式=-2x3+6x2-8x+x3+3x2
=-x3+9x2-8x.
(3)3a·(a2+2a)-2a2(a-3).
解:原式=3a3+6a2-2a3+6a2
=a3+12a2.
8.解方程:2x(x+1)-(3x-2)x=1-x2.
解:去括号,得2x2+2x-3x2+2x=1-x2,
整理,得4x=1,
解得x=.
(2)当x=2时,先化简:A+B,再求其值.
解:(2)A+B=x+(6x2-4x-2)
=6x2-x-2,
当x=2时,
原式=6×22-×2-2=15.
9.已知A=x,B是多项式,王虎同学在计算A+B 时,误把A+B看成了A×B,结果得3x3-2x2-x.
(1)求多项式B;
解:(1)由题意可知:x·B=3x3-2x2-x,
∴B=6x2-4x-2;
一、选择题
10.(1)下列各式中,计算正确的有( B )
①(a-3b)(-6a)=-6a2+18ab;
②(-9xy+2)=3x3y2+2;
③(-4ab)=2a3b2;
④=ab2-2ab.
B
A.1个 B.2个 C.3个 D.4个
(2)已知a-b=3,b-c=-2,则代数式a2-ac-b(a-c)的值为( C )
A.4 B.-4 C.3 D.-3
C
二、填空题
11.若(mx2-nx+2)·(-2x2)-4x3的结果中不含x4和x3的项,则m= 0 ,n= 2 .
12.通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据如图所示的图形写出一个代数恒等式: 2a(a+b)=2a2+2ab .
第12题图
0
2
2a(a+b)=2a2+2ab
三、解答题
13.已知有理数a、b、c满足|a-b-3|+(b+1)2+|c-1|=0,求(-3ab)(a2c-6b2c)的值.
解:由|a-b-3|+(b+1)2+|c-1|=0,
得:,解得:,
∵(-3ab)(a2c-6b2c)=-3a3bc+18ab3c,
∴当a=2,b=-1,c=1时,
原式=-3×23×(-1)×1+18×2×(-1)3×1
=24-36
=-12.
14.已知ab=3,求(2a3b2-3a2b+4a)(-2b)的值.
解:(2a3b2-3a2b+4a)(-2b)
=-4a3b3+6a2b2-8ab
=-4(ab)3+6(ab)2-8ab
=-4×33+6×32-8×3
=-108+54-24
=-78.
解答题
15.若m2+m-1=0,求代数式m3+2m2+2023的值.
解:∵m2+m-1=0,
∴m2+m=1,m2=1-m,
∴m3+2m2+2023
=m(1-m)+2m2+2023
=m-m2+2m2+2023
=m2+m+2023
=2024.
谢 谢 观 看
第6课时 整式的乘法(3)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算(x+1)(x-2)的结果是( B )
A.x2+x-2 B.x2-x-2
C.x2+2 D.x2-2
(2)计算(x+1)(2x-5)的结果是( A )
A.2x2-3x-5 B.2x2-6x-5
C.2x2-3x+5 D.x2-3x-5
B
A
(3)计算:(3m+5)(-3m-5)=( C )
A.9m2-25
B.-9m2-25
C.-9m2-30m-25
D.-9m2+30m-25
C
2.(1)若(x+2)(x+a)=x2-bx-8,则ab的值为( D )
A.-8 B.-4 C. D.16
(2)将多项式(x2+x-3)(x2-2x+2a)展开,常数项为-30,则a=( C )
A.3 B.4 C.5 D.6
(3)若(x+1)(2x2-ax+1)的运算结果中,x2的系数为-6,则a的值是( C )
A.4 B.-4 C.8 D.-8
(4)要使多项式(x+p)(x-q)不含x的一次项,则p与q的关系是( A )
A.相等 B.互为相反数
C.互为倒数 D.乘积为-1
D
C
C
A
二、填空题
3.计算:(5m+2)(2m-1)= 10m2-m-2 .
4.若(x+a)(x+b)=x2+6x+5,则a+b的值为 6 .
5.已知三角形的底边是(6a+2b)cm,高是(2b-3a)cm,则这个三角形的面积是 (-9a2+3ab+2b2) cm2.
10m2-m-2
6
(-9a2+3ab+2b2)
三、解答题
6.计算:
(1)(a+1)(a-6);
解:原式=a2-6a+a-6
=a2-5a-6.
(2)(2y+3)(y-1);
解:原式=2y2-2y+3y-3
=2y2+y-3.
(3)(m+2n)(2m-n);
解:原式=2m2-mn+4mn-2n2
=2m2+3mn-2n2.
(4)(x+3y-4)(2x-y).
解:原式=2x2-xy+6xy-3y2-8x+4y
=2x2+5xy-3y2-8x+4y.
7.计算下列各题:
(1)6x(x2+2)-x(3x-2)(2x-3);
解:原式=6x3+12x-(3x2-2x)(2x-3)
=6x3+12x-(6x3-9x2-4x2+6x)
=6x3+12x-6x3+9x2+4x2-6x
=13x2+6x.
(2)(3y+2)(y-4)-(y-2)(y-3).
解:原式=3y2+2y-12y-8-(y2-5y+6)
=3y2-10y-8-y2+5y-6
=2y2-5y-14.
8.已知A=1+2x,B=1-2x+4x2,C=1-4x3.
(1)化简:A·B-C;
解:(1)∵A=1+2x,B=1-2x+4x2,C=1-4x3,
∴A·B-C
=(1+2x)(1-2x+4x2)-1+4x3
=1-2x+4x2+2x-4x2+8x3-1+4x3
=12x3;
(2)当x=-时,求A·B-C的值.
解:(2)由(1)得A·B-C=12x3,
当x=-时,
原式=12×(-)3=-.
一、选择题
9.若不管a取何值,多项式a3+2a2-a-2与(a2-ma+2n)(a+1)都相等,则m,n的值分别为( A )
A.-1,-1 B.-1,1
C.1,-1 D.1,1
A
二、填空题
10.如图,现有正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),若要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙),且卡片全部用上,则拼成的大长方形有 11 种.
第10题图
11
三、解答题
11.若(x2+px+8)(x2-3x-q)的展开式中不含x3和x2的项,求2p+q的值.
解:(x2+px+8)(x2-3x-q)
=x4-3x3-qx2+px3-3px2-pqx+8x2-24x-8q
=x4+(-3+p)x3+(-q-3p+8)x2+(-pq-24)x-8q,
∵展开式中不含x3和x2的项,
∴,
解得:p=3,q=-1,
∴2p+q=6-1=5.
解答题
12.你能化简(x-1)(x99+x98+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
(x-1)(x+1)= ;
(x-1)(x2+x+1)= ;
(x-1)(x3+x2+x+1)= ;
…,
(x-1)(x99+x98+…+x+1)= .
解:(1)(x-1)(x+1)=x2+x-x-1=x2-1;
(x-1)(x2+x+1)=x3+x2+x-x2-x-1=x3-1;
(x-1)(x3+x2+x+1)=x4+x3+x2+x-x3-x2-x-1=x4-1;
…,
(x-1)(x99+x98+…+x+1)=x100+x99+…+x2+x-(x99+x98+…+x+1)=x100-1,
故答案为:x2-1;x3-1;x4-1;x100-1;
(2)请你利用上面的结论计算:299+298+…+2+1.
解:(2)原式=(2-1)×(299+298+…+2+1)
=2100-1.
谢 谢 观 看
第7课时 整式的乘法(4)
第十四章 整式的乘法与因式分解
一、选择题
1.下列运算正确的是( C )
A.(a3)2=a5 B.a3·a2=a6
C.(ab)4=a4b4 D.a6÷a3=a2
2.下列各式的运算结果是x6的是( C )
A.x4+x2 B.x12÷x2 C.(x2)3 D.x2·x3
C
C
3.(1)计算:x5÷x2=( B )
A.x2 B.x3 C.2x D.x7
(2)计算(2xy2)3÷2xy2的结果是( D )
A.3 B.3xy2 C.8xy D.4x2y4
4.若2x=5,2y=3,则22x-y的值为( B )
A.25 B. C.9 D.75
B
D
B
二、填空题
5.计算:(-5)8·(-5)6÷(-5)12= 25 .
6.(1)若ax÷a3·a5=a6,则x= 4 ;
(2)已知a5=6,a2=2,则a3= 3 ;
(3)已知(3x+1)0=1,则x满足的条件是 x≠- .
25
4
3
x≠-
三、解答题
7.计算:
(1)÷y5;
解:原式=y6÷y5
=y.
(2)(-a2b4)8÷(-a2b4)2.
解:原式=(-a2b4)6
=a12b24.
8.计算下列各题:
(1)(-a2)3+a2·a3+a8÷(-a2);
解:原式=-a6+a5-a6
=-2a6+a5.
(2)x3·x6+x20÷x10-xn+8÷xn-1;
解:原式=x9+x10-x9
=x10.
(3)y4+(y2)4÷y4-(-y2)2;
解:原式=y4+y8÷y4-y4
=y4+y4-y4
=y4.
(4)x3·x5-(2x4)2+x10÷x2.
解:原式=x8-4x8+x8
=-2x8.
9.(1)已知2×8x×16=223,求x的值;
解:∵2×8x×16=223,
∴2×(23)x×24=223,
∴2×23x×24=223,
∴1+3x+4=23,
解得x=6.
①am+n的值;
②a3m-2n的值.
解:①am+n=am·an
=5×3=15;
②a3m-2n=a3m÷a2n
=(am)3÷(an)2
=33÷52
=.
(2)已知am=3,an=5,求:
一、填空题
10.(1)已知10a=20,10b=,则3a÷3b= 9 ;
(2)已知5x=6,5y=3,则5x+2y-1= ;
(3)已知25a·52b=56,4b÷4c=4,则代数式a2+ab+3c的值是 6 ;
(4)已知2m=4n-1,27n=3m-1,则n-m= 5 .
9
6
5
二、解答题
11.解答下列各题:
(1)若3x=4,3y=6,求92x-y+27x-y的值;
解:∵3x=4,3y=6,
∴92x-y+27x-y
=(32)2x-y+(33)x-y
=34x-2y+33x-3y
=(3x)4÷(3y)2+(3x)3÷(3y)3
=+
=.
(2)若26=a2=4b,求a+b的值.
解:26=(±23)2=(±8)2,
26=(22)3=43,
∵26=a2=4b,
∴a=±8,b=3,
∴a+b=11或-5.
解答题
12.(1)若33·9m+4÷272m-1的值为729,试求m的值;
解:∵33·9m+4÷272m-1
=33·32(m+4)÷33(2m-1)
=33+2(m+4)-3(2m-1)
=314-4m
=729
=36,
∴14-4m=6,
解得m=2.
(2)已知3m=4,3m-4n=,求200n的值;
解:∵3m=4,
∴3m-4n=3m÷34n=4÷34n=,
∴34n=81=34,
∴4n=4,即n=1,
∴200n=200.
(3)若mp=,m2q=7,mr=-,求m3p+4q-2r的值.
解:∵mp=,m2q=7,mr=-,
∴m3p+4q-2r
=(mp)3×(m2q)2÷(mr)2
=()3×72÷(-)2
=×72×
=.
谢 谢 观 看
第8课时 整式的乘法(5)
第十四章 整式的乘法与因式分解
一、选择题
1.计算(-4x3+2x)÷2x的结果正确的是( A )
A.-2x2+1 B.2x2+1
C.-2x3+1 D.-8x4+2x
2.2x3可以表示为( C )
A.x3·x3 B.2x4-x
C.x3+x3 D.2x6÷x2
A
C
4.面积为9a2-6ab+3a的长方形一边长为3a,另一边长为( D )
A.2a-3 B.2a-3b+1
C.3a-2b D.3a-2b+1
D
3.已知8a3bm÷28an+1b2=b2,则m,n的值分别为( B )
A.4,3 B.4,2 C.2,2 D.2,3
B
二、填空题
5.若8a5bn÷2amb=4a2b5,则mn= 18 .
6.已知长方形的面积为6a2b-4a2+2a,宽为2a,则长方形的周长为 6ab+2 .
18
6ab+2
三、解答题
7.计算:
(1)8x8÷2x3;
解:原式=4x5.
(2)20x3y5z÷(-5x2y3);
解:原式=-4xy2z.
(3)(-4a5b3)2÷8a2b3;
解:原式=16a10b6÷8a2b3
=2a8b3.
(4)9a5b4÷3a2b4-a·(-5a2);
解:原式=3a3+5a3
=8a3.
(5)-2x6-·8x5+(2x4)3÷(-x)5;
解:原式=-2x6-x2·8x5+8x12÷(-x5)
=-2x6-2x7-8x7
=-2x6-10x7.
(6)3a2b2÷a2+b·(a2b-3ab)-(2b)2.
解:原式=3b2+a2b2-3ab2-4b2
=-b2+a2b2-3ab2.
8.计算:
(1)(4m3-3m2n+2m)÷2m;
解:原式=2m2-mn+1.
(2)÷;
解:原式=-6x+2y-1.
(3)[6(m+n)a+3z4-6(m+n)a-2z2+3(m+n)a-1z]÷3(m+n)a-2z;
解:原式=2(m+n)5z3-2z+m+n.
(4)(3x4-2x3)÷(-x)-(x-x2)·3x.
解:原式=-3x3+2x2-(3x2-3x3)
=-3x3+2x2-3x2+3x3
=-x2.
一、选择题
9.已知x3+(a-1)x-6能被x-2整除,则a的值为( C )
A.1 B.-1 C.0 D.2
C
二、填空题
10.若-5a2m-3bn+4÷3am+2b5=-a4b2,则m÷n= 3 .
3
三、解答题
11.先化简,再求值:[(2x+y)(2x-y)-3(2x2-xy)+y2]÷,其中x=2,y=-1.
解:原式=(4x2-y2-6x2+3xy+y2)÷
=(-2x2+3xy)÷
=4x-6y,
当x=2,y=-1时,
原式=8+6=14.
12.阅读材料:
∵(x-2)(x+3)=x2+x-6,
∴(x2+x-6)÷(x-2)=x+3,
即x2+x-6能被x-2整除,
∴x-2是x2+x-6的一个因式,且当x=2时,x2+x-6=0.
解答问题:
(1)由(x+2)(x+3)=x2+5x+6,得x2+5x+6能被 整除,且当x= 时,x2+5x+6=0;
解:(1)∵(x+2)(x+3)=x2+5x+6,
∴x2+5x+6能被x+2整除或者能被x+3整除,
当x=-2或-3时,x2+5x+6=0,
故答案为:x+2或x+3,-2或-3;
x+2或x+3
-2或-3
(2)根据材料,已知多项式x2+mx-14能被x+2整除,试求m的值.
解:(2)∵x2+mx-14能被x+2整除,
当x=-2时,
原式=(-2)2+m×(-2)-14=0,
解得m=-5.
解答题
13.(1)计算:(a6b2)n+1÷(-anb)3÷a2n-3bn;
解:原式=a6n+6b2n+2÷(-a3nb3)÷a2n-3bn
=-a3n+6b2n-1÷a2n-3bn
=-an+9bn-1.
(2)已知(xmyn)2÷(x2y)3=x4y5,求2m-n的值;
解:∵(xmyn)2÷(x2y)3=x2m-6y2n-3=x4y5,
∴2m-6=4,2n-3=5,
解得:m=5,n=4,
则2m-n=2.
(3)计算:÷[3(-x-y)2(x-y)2]2.
解:原式=36(x+y)6(x-y)4÷[9(x+y)4(x-y)4]
=4(x+y)2
=4x2+8xy+4y2.
谢 谢 观 看
第9课时 专题幂的运算
第十四章 整式的乘法与因式分解
解答题
1.计算:
(1)×;
解:原式=
=.
(2)xm+15·xm-1;
解:原式=x(m+15)+(m-1)
=x2m+14.
(3)(-x)·(-x)6;
解:原式=(-x)7
=-x7.
(4)-m3·m4;
解:原式=-m3+4
=-m7.
(5)(3ab7)2;
解:原式=9a2b14.
(6)(-m)8÷(-m)3;
解:原式=(-m)5
=-m5.
(7)(xy)7÷(xy)4;
解:原式=(xy)3
=x3y3.
(8)x2m+2÷xm+2;
解:原式=x2m+2-m-2
=xm.
解:原式=(2a+b)(2n+1)+3+(n-4)
=(2a+b)3n.
(11)(x-y)2·(y-x)5.
解:原式=(y-x)2·(y-x)5
=(y-x)7.
(9)(x-y)5÷(y-x)3;
解:原式=-(y-x)5÷(y-x)3
=-(y-x)2.
(10)(2a+b)2n+1·(2a+b)3·(2a+b)n-4;
2.计算:
(1)x4·(-x)5+(-x)4·x5;
解:原式=-x9+x9
=0.
(2)(m4)2+m5·m3+(-m)4·m4;
解:原式=m4×2+m5+3+m4+4
=3m8.
(3)(-3a2)3+(-4a3)2;
解:原式=-27a6+16a6
=-11a6.
(4)x·(x2)2+x7÷x2-4x3·x2;
解:原式=x5+x5-4x5
=-2x5.
(5)(-3a4)2-a·a3·a4-a10÷a2;
解:原式=9a8-a8-a8
=7a8.
(6)0.254×44-×;
解:原式=(0.25×4)4-×
=1-×
=1-1×
=.
(5)(-3a4)2-a·a3·a4-a10÷a2;
解:原式=9a8-a8-a8
=7a8.
(7)×24+(-2)0-(-0.1)2024×102024;
解:原式=×2+1-(-0.1×10)2024
=-2+1-1
=-2.
(8)(a-b)2·(b-a)3+(a-b)4·(b-a).
解:原式=(b-a)5+(b-a)5
=2(b-a)5.
3.(1)已知xa+b=6,xb=3,求xa的值;
解:xa=xa+b-b=xa+b÷xb=6÷3=2.
(2)已知xm=5,xn=7,求x2m+n的值;
解:∵xm=5,xn=7,
∴x2m+n=xm·xm·xn=5×5×7=175.
(3)已知2x+3y-2=0,求9x·27y的值;
解:∵2x+3y-2=0,∴2x+3y=2,
∴9x·27y=32x·33y=32x+3y=32=9.
(4)已知10m=20,10n=4,求2m-n的值;
解:∵102m-n==100=102,
∴2m-n=2.
(5)若32·92a+1÷27a+1=81,求a的值;
解:∵32·92a+1÷27a+1=81,
∴32·32(2a+1)÷33(a+1)=34,
即2+2(2a+1)-3(a+1)=4,
解得a=3.
(6)若33x+1·53x+1=152x+4,求x的值.
解:33x+1·53x+1=153x+1=152x+4,
∴3x+1=2x+4,
∴x=3.
4.比较312×510与310×512的大小.
解:312×510=(3×5)10×32,
310×512=(3×5)10×52,
∵32<52,
∴312×510<310×512.
谢 谢 观 看
第10课时 专题整式的乘除
第十四章 整式的乘法与因式分解
解答题
1.计算:
(1)(-12a2b)÷2ab;
解:原式=-6a.
(2)(-2xy2)2·3x2y;
解:原式=4x2y4·3x2y
=12x4y5.
(3)5(a4)3+(-2a3)2·(-a6);
解:原式=5a12-4a6·a6
=a12.
(4)2x3y·(-2xy)+÷2x2.
解:原式=-4x4y2-8x9y3÷2x2
=-4x4y2-4x7y3.
2.计算:
(1)·ab;
解:原式=a2b3-a2b2.
(2)(-2a2)(3ab2-5ab3);
解:原式=-6a3b2+10a3b3.
(3)-3x·;
解:原式=-x3y3-6xy2+3x.
(4)·5xy2÷(-10x6y5)+(x2y-2xy)÷xy.
解:原式=8x6y3·5xy2÷(-10x6y5)+x-2
=40x7y5÷(-10x6y5)+x-2
=-4x+x-2
=-3x-2.
3.计算:
(1)(x-2)(x+3);
解:原式=x2+3x-2x-6
=x2+x-6.
(2)(3x+9)(6x-8);
解:原式=18x2-24x+54x-72
=18x2+30x-72.
(3)(a+b+1)(2a-b);
解:原式=2a2-ab+2ab-b2+2a-b
=2a2+ab+2a-b2-b.
(4)(2a-7)(a+6)-(a-2)(2a+1);
解:原式=2a2+12a-7a-42-(2a2+a-4a-2)
=2a2+5a-42-2a2+3a+2
=8a-40.
(5)(x-2)(x+1)-2(x-3)(x+2).
解:原式=x2+x-2x-2-2x2-4x+6x+12
=-x2+x+10.
4.(1)计算:(-3a2b3)÷;
解:原式=(-3a2b3)÷(3ab-ab2-2ab+ab2)
=(-3a2b3)÷ab
=-3ab2.
(2)先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
解:原式=6a3-12a2+9a-6a3-8a2
=-20a2+9a,
当a=-2时,
原式=-20×4-9×2=-98.
5.将多项式(x-2)(x2+ax-b)展开后不含x2和x的项,试求2a2-b的值.
解:原式=x3+ax2-bx-2x2-2ax+2b
=x3+(a-2)x2-(2a+b)x+2b,
∵多项式不含x2和x的项,
∴a-2=0,-(2a+b)=0,
∴a=2,b=-4,
∴2a2-b=2×22+4=12.
6.解不等式组:
.
解:不等式组可化为:
,
解不等式①得:x<,
解不等式②得:x<-1,
∴不等式组的解集为x<-1.
7.长方形的长为a厘米,宽为b厘米,其中a>b,如果将原长方形的长和宽各增加3厘米,得到的新长方形的面积为S1平方厘米,如果将原长方形的长和宽分别减少2厘米,得到的新长方形的面积为S2平方厘米.
(1)若a、b为正整数,请说明:S1与S2的差一定是5的倍数;
解:(1)由题意得:
S1=(a+3)(b+3)=ab+3(a+b)+9,
S2=(a-2)(b-2)=ab-2(a+b)+4,
∴S1-S2=ab+3(a+b)+9-ab+2(a+b)-4
=5(a+b)+5=5(a+b+1),
∴S1与S2的差一定是5的倍数;
(2)如果S1=2S2,求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积;
解:(2)∵S1=2S2,
∴ab+3a+3b+9=2(ab-2a-2b+4),
∴ab-7a-7b-1=0,
∴ab-7a-7b=1,
∵新长方形的面积为(a-7)(b-7)=ab-7a-7b+49=1+49=50平方厘米,
∴将原长方形的长和宽分别减少7厘米后得到的新长方形的面积为50平方厘米;
(3)如果用一个面积为S1的长方形和两个面积为S2的长方形恰好能没有缝隙没有重叠地拼成一个正方形,求a,b的值.
解:(3)由题意可得方程组:,
或,
解得或(不符合题意,舍),
∴a的值为7,b的值为4.5.
谢 谢 观 看
第11课时 平方差公式
第十四章 整式的乘法与因式分解
一、选择题
1.下列式子中可以用平方差公式计算的是( D )
A.(x+2)(x+2) B.(x+2)(-x-2)
C.(x-2)2 D.(x+2)(x-2)
2.下列计算正确的是( C )
A.x3+4x3=5x6
B.a2·a3=a6
C.(-2x3)4=16x12
D.(x+2y)(x-2y)=x2-2y2
D
C
3.若a-b=3,a2-b2=-9,则a+b=( D )
A.2 B.3 C.-2 D.-3
4.如图,边长为a的正方形中剪去一个边长为b的小正方形,剩下部分正好拼成一个等腰梯形,利用这两幅图形阴影部分的面积,能验证的数学公式是( A )
A.a2-b2=(a+b)(a-b)
B.(a+b)2-(a-b)2=4ab
C.(a+b)2=a2+2ab+b2
D.(a-b)2=a2-2ab+b2
第4题图
D
A
二、填空题
5.计算:2024×2022-20232= -1 .
6.若a2-4b2=12,且a-2b=-3,则a+b= -3.75 .
-1
-3.75
三、解答题
7.计算:
(1)(a+5)(a-5);
解:原式=a2-25.
(2)(x-2y)(2y+x);
解:原式=x2-4y2.
(3)(3m-2n)(-3m-2n);
解:原式=-(3m-2n)(3m+2n)
=-(9m2-4n2)
=4n2-9m2.
(4)(5ab-3xy)(-3xy-5ab);
解:原式=-(5ab-3xy)(5ab+3xy)
=-(25a2b2-9x2y2)
=9x2y2-25a2b2.
(5)(x3+2)(x3-2).
解:原式=(x3)2-22
=x6-4.
8.计算:
(1)20232-2022×2024;
解:原式=20232-(2023-1)(2023+1)
=20232-20232+12
=1.
(2)(5m+2)(5m-2)-(3m+1)(2m-1).
解:原式=(25m2-4)-(6m2-3m+2m-1)
=25m2-4-6m2+m+1
=19m2+m-3.
9.(1)已知m2-n2=24,m+n=8,求m-n的值;
解:∵m2-n2=(m+n)(m-n)=24,m+n=8,
∴m-n=3.
(2)先化简,再求值:(x+2y)(x-2y)-(2x-y)(-2x-y),其中x=8,y=-8.
解:原式=x2-4y2-y2+4x2
=5x2-5y2,
∵x=8,y=-8,
∴原式=5×82-5×(-8)2=0.
一、填空题
10.计算:(5+1)(52+1)(54+1)(58+1)(516+1)+= .
11.已知a1=(1+)(1-),a2=(1+)(1-),a3=(1+)(1-),…,an=(1+)(1-),Sn=a1·a2·a3·…·an,则2S2023= .
二、解答题
12.计算下列各题:
(1)1002-992+982-972+962-952+…+22-12;
解:原式=(100+99)(100-99)+(98+97)(98-97)+(96+95)(96-95)
+…+(2+1)(2-1)
=100+99+98+97+…+2+1
=5050.
(2)++…+.
解:原式=++…+
=-1×
=-50.
解答题
13.(1)计算并观察下列各式:
第1个:(a-b)(a+b)= ;
第2个:(a-b)(a2+ab+b2)= ;
第3个:(a-b)(a3+a2b+ab2+b3)= ;
……,
这些等式反映出多项式乘法的某种运算规律;
解:(1)a2-b2;a3-b3;a4-b4;
(2)猜想:若n为大于1的正整数,则(a-b)(an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1)= ;
an-bn
(3)利用(2)的猜想计算:2n-1+2n-2+2n-3+…+23+22+1= ;
2n-3
(4)拓展与应用:计算3n-1+3n-2+3n-3+…+33+32+1的值.
解:原式=×(3-1)(3n-1+3n-2+3n-3+…+33+32+3+1)-3
=×(3n-1n)-3
=.
谢 谢 观 看
第12课时 完全平方公式(1)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算:(c-a)2=( D )
A.c2-a2 B.a2+2ac+c2
C.c2+a2 D.c2-2ac+a2
(2)计算:(-a-b)2=( B )
A.a2+b2 B.a2+2ab+b2
C.a2-b2 D.a2-2ab+b2
D
B
(4)若(7x-a)2=49x2-bx+9,则|a+b|的值为( D )
A.18 B.24 C.39 D.45
D
(3)计算(x+2)2的结果为x2+□x+4,则“□”中的数为( D )
A.-2 B.2 C.-4 D.4
D
2.下列各式能写成两数和的平方的是( D )
A.x2+2x-1 B.1+x2
C.x2+x+1 D.x2+4x+4
3.如图,将图1中阴影部分拼成图2,根据两个图形中阴影部分的关系,下列计算公式可以表示该关系的是( B )
A.(a+b)(a-b)=a2-b2
B.(a-b)2=a2-2ab+b2
C.(a+b)2=a2+2ab+b2
D.(a+b)2=(a-b)2+4ab
第3题图
D
B
二、填空题
4.填上适当的数或代数式,使等式成立:
(1)x2+10x+ 25 =(x+ 5 )2;
(2)m2-8m+ 16 =(m- 4 )2;
(3)x2+xy+ y2 =(x+ y )2.
25
5
16
4
y2
y
三、解答题
5.计算:
(1)(2a+3b)2;
解:原式=(2a)2+2·2a·3b+(3b)2
=4a2+12ab+9b2.
(2)(-2m+n)2;
解:原式=(-2m)2-2·2m·n+n2
=4m2-4mn+n2.
(3)(-2m-n)2.
解:原式=(-2m)2+2(-2m)(-n)+(-n)2
=4m2+4mn+n2.
6.计算:
(1)(2a+b)2-(2a-b)2;
解:原式=4a2+4ab+b2-(4a2-4ab+b2)
=8ab.
(2)(3x-5)2-(2x+7)2.
解:原式=9x2-30x+25-(4x2+28x+49)
=9x2-30x+25-4x2-28x-49
=5x2-58x-24.
7.解方程:-=1.
解:去括号得:x2+x+-x2+=1,
解得:x=.
8.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆形钢板,求剩下的钢板的面积.
第8题图
解:剩下的钢板的面积为π-π-=πab.
一、选择题
9.若n为正整数,则(2n+1)2-(2n-1)2( B )
A.一定能被6整除
B.一定能被8整除
C.一定能被10整除
D.一定能被12整除
B
二、填空题
10.(1)若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k= -3 ;
(2)若x2-2(k-1)x+9是完全平方式,则k的值为 4或-2 .
-3
4或-2
三、解答题
11.计算:
(1)(2x-1)(4x2-1)(2x+1);
解:原式=(4x2-1)(4x2-1)
=(4x2-1)2
=16x4-8x2+1.
(2)(x+y)2-4(x+y)(x-y)+4(x-y)2;
解:原式=[x+y-2(x-y)]2
=(3y-x)2
=x2-6xy+9y2.
(3)4(a+2)2-7(a+3)(a-3)+3(a-1)2.
解:原式=4(a2+4a+4)-7(a2-9)+3(a2-2a+1)
=4a2+16a+16-7a2+63+3a2-6a+3
=10a+82.
解答题
12.如图,大正方形、小正方形的边长分别为a、b.
(1)用含a、b的代数式表示阴影部分的面积S;
解:(1)∵大正方形、小正方形的边长分别为a、b,
∴S=a2+b2-a2-(a+b)b
=a2+b2-ab;
第12题图
(2)如果a+b=9,ab=6,求阴影部分的面积.
解:(2)∵a+b=9,ab=6,
∴S=a2+b2-ab
=(a+b)2-ab
=×92-×6
=,
故阴影部分的面积为.
第12题图
谢 谢 观 看
第13课时 完全平方公式(2)
第十四章 整式的乘法与因式分解
一、选择题
1.计算(x-2)2正确的是( D )
A.x2-4 B.x2-4x-4
C.x2-2x+4 D.x2-4x+4
2.将10.52变形正确的是( C )
A.10.52=102+0.52
B.10.52=(11+0.5)(11-0.5)
C.10.52=102+2×10×0.5+0.52
D.10.52=112-11×0.5+0.52
D
C
3.若x2+(a-1)x+25是一个完全平方式,则a的值为( B )
A.-9 B.-9或11
C.9或-11 D.11
4.若ab=1,a+b=3,则2a2+2b2的值是( D )
A.7 B.10 C.12 D.14
B
D
二、填空题
5.(1)若a2+b2=19,a+b=5,则ab= 3 ;
(2)若a2+b2=13,(a-b)2=1,则(a+b)2= 25 .
3
25
三、解答题
6.计算:
(1)9992;
解:原式=(1000-1)2
=1000000-2000+1
=998001.
(2)1.23452+0.76552+2.469×0.7655.
解:原式=1.23452+2×1.2345×0.7655+0.76552
=(1.2345+0.7655)2
=4.
7.计算:
(1);
解:原式=
=
=1-x2+x4.
(2)(3x+2y-4)(2y-3x+4);
解:原式=[2y+(3x-4)][2y-(3x-4)]
=(2y)2-(3x-4)2
=4y2-9x2+24x-16.
(3)(m-n-3)2.
解:原式=(m-n)2+2(m-n)×(-3)+9
=m2+n2-2mn+6n-6m+9.
8.(1)已知xy=1,x-y=5,求x2+y2的值;
解:将x-y=5两边同时平方,
得:(x-y)2=25,
即x2+y2-2xy=25,
∵xy=1,
∴x2+y2=25+2xy=27.
(2)已知a-=4,求a2+的值.
解:将a-=4两边同时平方,
得:=42=16,
即a2+-2=16,
∴a2+=16+2=18.
一、填空题
9.多项式1+4a2加上一个单项式后,使它成为一个整式的完全平方式,则单项式可以为 4a4(或±4a或-1或-4a2) .(写出一个即可)
10.已知(a-2022)2+(2023-a)2=5,则(a-2022)(a-2023)= 2 .
11.如果a+b+|-1|=4+2-4,那么a+2b-3c= 0 .
4a4(或±4a或-1或-4a2)
2
0
二、解答题
12.比较代数式2x2+5x-1与代数式x2+7x-4的值的大小.
解:(2x2+5x-1)-(x2+7x-4)
=2x2+5x-1-x2-7x+4
=x2-2x+3
=(x-1)2+2,
∵(x-1)2+2>0,
∴代数式2x2+5x-1的值比代数式x2+7x-4的值大.
解答题
13.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例,如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应(a+b)3=a3+3a2b+3ab2+b3展开式中的系数.
根据上述规律,解答下列问题:
(1)求(a+b)5的展开式;
解:(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
第13题图
(2)计算:25+5×24+10×23+10×22+5×2+1;
解:(2)25+5×24+10×23+10×22+5×2+1
=25+5×24×1+10×23×12+10×22×13+5×2×14+15
=(2+1)5
=35;
第13题图
(3)若(x+1)5·(2x2+ax-b)(a、b为常数)的展开式中不含x2和x的项,求a、b的值.
解:(3)(x+1)5=x5+5x4+10x3+10x2+5x+1,
∵展开式中不含x2和x的项,
∴取(10x2+5x+1)(2x2+ax-b)
=20x4+10ax3-10bx2+10x3+5ax2-5bx+2x2+ax-b
=20x4+(10a+10)x3+(-10b+5a+2)x2+(-5b+a)x-b,
∴含x2的项的系数为-10b+5a+2=0,
含x的项的系数为-5b+a=0,
∴a=-,b=-.
谢 谢 观 看
第14课时 专题乘法公式
第十四章 整式的乘法与因式分解
解答题
1.计算:
(1)(x-3)(x+3);
解:原式=x2-9.
(2)(x+3y)(x-3y);
解:原式=x2-9y2.
(3);
解:原式=-22
=x6-4.
(4)(2m-n)(-2m-n);
解:原式=(n-2m)(n+2m)
=n2-4m2.
(5)101×99;
解:原式=(100+1)(100-1)
=1002-1
=9999.
(6)145.52-135.52.
解:原式=(145.5+135.5)(145.5-135.5)
=281×10
=2810.
2.计算:
(1)(4m+n)2; (2);
解:原式=16m2+8mn+n2;
解:原式=y2-y+.
(3)(-2x+5)2; (4);
解:原式=4x2-20x+25;
解:原式=x2-xy+y2.
(5)1022; (6)992.
解:原式=(100+2)2
=10000+400+4
=10404;
解:原式=(100-1)2
=10000-200+1
=9801.
3.计算:
(1)(x+2y)2(x-2y)2;
解:原式=[(x+2y)(x-2y)]2
=(x2-4y2)2
=x4-8x2y2+16y4.
(2)(1-3y)(1+3y)(1+9y2);
解:原式=(1-9y2)(1+9y2)
=1-81y4.
(3)1232-122×124;
解:原式=1232-(123-1)(123+1)
=1232-(1232-1)
=1.
(4)(3-2x+y)(3+2x-y).
解:原式=[3-(2x-y)][3+(2x-y)]
=9-(2x-y)2
=9-4x2+4xy-y2.
4.(1)计算:[(a-2b)(a+2b)-(2b-a)2]÷(-4b);
解:原式=(a2-4b2-4b2+4ab-a2)÷(-4b)
=(-8b2+4ab)÷(-4b)
=2b-a.
(2)先化简,再求值:(2x+3y)(2x-3y)-4x(x-y)+(x-2y)2,其中x,y满足x2-6x+9+|2y-1|=0;
解:原式=4x2-9y2-4x2+4xy+x2-4xy+4y2
=x2-5y2,
由题意得(x-3)2+|2y-1|=0,
∴x-3=0,2y-1=0,解得x=3,y=,
∴原式=9-=.
(3)已知x2+y2-2x+6y+10=0,求x+y的值;
解:原方程变形为:x2-2x+1+y2+6y+9=0,
即(x-1)2+(y+3)2=0,
∴x-1=0,y+3=0,
∴x=1,y=-3,
∴x+y=-2.
解:①原式=(x+y)2-2xy,
当x+y=5,xy=-3时,
原式=25-2×(-3)
=31;
②原式=1-y-x+xy
=1-(x+y)+xy,
当x+y=5,xy=-3时,
原式=1-5+(-3)
=-7.
(4)已知x+y=5,xy=-3,求:
①x2+y2的值;
②(1-x)(1-y)的值.
5.计算:(1-)(1-)…(1-)(1-).
解:原式=(1-)(1+)(1-)(1+)×…×(1-)(1+)(1-)
(1+)
=××××…××××
=×
=.
6.阅读理解:
若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值.
解:设80-x=a,x-60=b,
则ab=(80-x)(x-60)=30,
a+b=80-x+x-60=20,
∴(80-x)2+(x-60)2=a2+b2=(a+b)2-2ab=202-2×30=340.
解决问题:
若x满足(30-x)(x-20)=-10,求(30-x)2+(x-20)2的值.
解:设30-x=a,x-20=b,
则ab=(30-x)(x-20)=-10,
a+b=30-x+x-20=10,
∴(30-x)2+(x-20)2
=a2+b2
=(a+b)2-2ab
=102-2×(-10)
=120.
谢 谢 观 看
第15课时 提公因式法
第十四章 整式的乘法与因式分解
一、选择题
1.下列从左到右的变形是分解因式的是( C )
A.3x+3y-5=3(x+y)-5
B.(x+1)(x-1)=x2-1
C.x2-9=(x+3)(x-3)
D.x2+1=x
2.多项式4xy3z-8x3y2的公因式是( D )
A.4xy B.-4xyz C.-4x2y D.4xy2
C
D
3.将x2+mx+n分解成(x-7)(x+2),则m,n的值分别为( D )
A.5,-14 B.-5,14
C.5,14 D.-5,-14
D
二、填空题
4.分解因式:3a2b+6ab+3b= 3b(a+1)2 .
5.若ab=-3,a-2b=5,则a2b-2ab2的值是 -15 .
3b(a+1)2
-15
三、解答题
6.分解因式:
(1)3x2y-6xy;
解:原式=3xy(x-2).
(2)5x2y3-25x3y2;
解:原式=5x2y2(y-5x).
(3)15x3y2+5x2y-20x2y3;
解:原式=5x2y(3xy+1-4y2).
(4)-4m3+16m2-26m;
解:原式=-2m(2m2-8m+13).
(5)-9x3y2-6x2y2+3xy;
解:原式=-3xy(3x2y+2xy-1).
(6)2m(a-b)-3n(a-b);
解:原式=(a-b)(2m-3n).
(7)8amb3-12am+1b2+16am+2b.
解:原式=4amb(2b2-3ab+4a2).
7.计算:123×6.28+628×1.32-15.5×62.8.
解:原式=6.28×(123+100×1.32-15.5×10)
=6.28×(123+132-155)
=628.
8.利用提公因式法先化简,再求值:(a-b)2+b(a-b),其中a=2,b=-.
解:原式=(a-b)[(a-b)+b]
=a(a-b)
=a2-ab,
当a=2,b=-时,
原式=22-2×=5.
解答题
9.分解因式:
(1)4a2n+1bm-6an+2bm-1(m、n为大于1的自然数);
解:原式=2an+2bm-1(2an-1b-3).
(2)3a(a+b)(a-b)-2b(b-a);
解:原式=3a(a+b)(a-b)+2b(a-b)
=(a-b)(3a2+3ab+2b).
(3)5a3b(a-b)3-10a4b3(b-a)2.
解:原式=5a3b(a-b)2(a-b-2ab2).
10.已知正整数n满足5n+2×2n+1-5n+1×2n+2=3000,求n的值.
解:∵5n+2×2n+1-5n+1×2n+2
=5×10n+1-2×10n+1
=3×10n+1,
∴3×10n+1=3000,
即10n+1=1000=103,
∴n=2.
11.计算:
(1);
解:原式=
=
=-23
=-8.
(2).
解:原式=
=.
解答题
12.阅读材料:
若一个整式A等于整式B与整式C之积,则称整式B和整式C为整式A的因式.
如:①∵36=4×9,∴4和9是36的因数;
∵x2-x-2=(x+1)(x-2),
∴x+1和x-2是x2-x-2的因式;
②若x+1是x2+ax-2的因式,求常数a的值.
解:∵x+1是x2+ax-2的因式,
∴存在一个整式mx+n,使得x2+ax-2=(x+1)(mx+n),
∵当x=-1时,(x+1)(mx+n)=0,
∴当x=-1时,x2+ax-2=0,
∴1-a-2=0,解得a=-1.
根据材料内容,解答下列问题:
(1)若x+5是整式x2+mx-10的一个因式,则m= ;
解:(1)∵x+5是整式x2+mx-10的一个因式,
∴当x=-5时,x2+mx-10=0,
即25-5m-10=0,
解得m=3.
3
(2)若整式x2-1是3x4-ax2+bx+1的因式,求的值.
解:(2)∵整式x2-1是3x4-ax2+bx+1的因式,
∴存在一个整式3x2+mx-1,使得3x4-ax2+bx+1=(x2-1)(3x2+mx-1),
∴当x=1时,(x2-1)(3x2+mx-1)=0,
即3x4-ax2+bx+1=0,
则3-a+b+1=0①,
当x=-1时,(x2-1)(3x2+mx-1)=0,
即3x4-ax2+bx+1=0,
则3-a-b+1=0②,
联立①②,解得a=4,b=0,
∴==2.
谢 谢 观 看
第16课时 公式法(1)
第十四章 整式的乘法与因式分解
一、选择题
1.下列多项式中,能用公式法分解因式的是( C )
A.x2-xy B.x2+xy C.x2-y2 D.x2+y2
2.因式分解x2y-4y的正确结果是( A )
A.y(x+2)(x-2) B.y(x+4)(x-4)
C.y(x2-4) D.y(x-2)2
3.已知a-b=1,则a2-b2-2b的值为( C )
A.4 B.3 C.1 D.0
C
A
C
二、填空题
4.分解因式:
(1)16x2-25= (4x+5)(4x-5) ;
(2)4a3b3-ab= ab(2ab+1)(2ab-1) ;
(3)-x2+2= -(x+2)(x-2) ;
(4)m2(x-2)+(2-x)= (x-2)(m+1)(m-1) .
5.计算:20232-20222= 4045 .
6.若|x+y-5|+(x-y+1)2=0,则x2-y2= -5 .
(4x+5)(4x-5)
ab(2ab+1)(2ab-1)
-(x+2)(x-2)
(x-2)(m+1)(m-1)
4045
-5
三、解答题
7.用平方差公式分解因式:
(1)36-x2;
解:原式=(6+x)(6-x).
(2)-a2+b2;
解:原式=(b+a)(b-a).
(3)x2-16y2;
解:原式=(x+4y)(x-4y).
(4)x2y2-z2;
解:原式=(xy+z)(xy-z).
(5)(x+2)2-9;
解:原式=(x+2+3)(x+2-3)
=(x+5)(x-1).
(6)a4-16;
解:原式=(a2+4)(a2-4)
=(a2+4)(a+2)(a-2).
(7)x2(x-2)+4y2(2-x).
解:原式=(x-2)(x2-4y2)
=(x-2)(x+2y)(x-2y).
8.已知x、y满足,求x2-y2的值.
解:,
①+②,得3x+3y=15,即x+y=5,
①-②,得x-y=3,
∴x2-y2=(x+y)(x-y)=15.
9.若n为整数,证明:(n+13)2-n2能被13整除.
证明:∵(n+13)2-n2
=(n+13-n)(n+13+n)
=13(2n+13),
∵n为整数,
∴(n+13)2-n2能被13整除.
一、填空题
10.如果(a2+b2+2)(a2+b2-2)=5,那么a2+b2= 3 .
11.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:x-y=0,x+y=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3-xy2,取x=13,y=3时,用上述方法产生的密码是: 131610(答案不唯一) .(写出一个即可)
3
131610
(答案不唯一)
二、解答题
12.把下列各式分解因式:
(1)(2x+3y)2-(3x+2y)2;
解:原式=(2x+3y+3x+2y)(2x+3y-3x-2y)
=(5x+5y)(-x+y)
=-5(x+y)(x-y).
(2)9(a+b)2-64(a-b)2.
解:原式=(3a+3b-8a+8b)(3a+3b+8a-8b)
=(11b-5a)(11a-5b).
13.(1)填空:a2-b2=(a-b)( );
a3-b3=(a-b)(a2+ab+b2);
a4-b4=(a-b)(a3+a2b+ab2+b3);
a5-b5=(a-b)( );
解:(1)a2-b2=(a-b)(a+b);
a3-b3=(a-b)(a2+ab+b2);
a4-b4=(a-b)(a3+a2b+ab2+b3);
a5-b5=(a-b)(a4+a3b+a2b2+ab3+b4),
(2)猜想:an-bn=(a-b)( );
(其中n为正整数,且n≥2)
an-1+an-2b+…+abn-2+bn-1
a+b
a4+a3b+a2b2+ab3+b4
(3)利用(2)猜想的结论化简:29+28+27+…+23+22+2.
解:(3)29+28+27+…+23+22+2
=(2-1)(29+28·1+27·12+…+23·16+22·17+2·18+19)-1
=210-1-1
=1024-2
=1022.
解答题
14.计算:
(1)++…+;
解:原式=++…+
=1-2+2-3+…+99-100
=1-100
=-99.
(2)(1-)(1-)(1-)…(1-)(1-).
解:原式=(1-)(1+)(1-)(1+)…(1-)(1+)(1-)
(1+)
=××××…××××
=×
=.
谢 谢 观 看
第17课时 公式法(2)
第十四章 整式的乘法与因式分解
一、选择题
1.下列各式中能用完全平方公式进行因式分解的是( D )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
2.分解因式:4x2+4x+1=( C )
A.4x(x+1)+1 B.(4x+1)2
C.(2x+1)2 D.(2x-1)2
D
C
3.分解因式(x-1)2-2(x-1)+1的结果是( D )
A.(x-1)(x-2) B.x2
C.(x+1)2 D.(x-2)2
D
二、填空题
4.分解因式:
(1)2a3-8a2+8a= 2a(a-2)2 ;
(2)3x2-6x+3= 3(x-1)2 ;
(3)3m2-6mn+3n2= 3(m-n)2 .
2a(a-2)2
3(x-1)2
3(m-n)2
三、解答题
5.分解因式:
(1)-x2+4xy-4y2;
解:原式=-(x2-4xy+4y2)
=-(x-2y)2.
(2)a2x-6ax+9x;
解:原式=x(a2-6a+9)
=x(a-3)2.
(3)-a2+ab-b2;
解:原式=-(a-b)2.
(4)(x-y)2+4xy;
解:原式=(x+y)2.
(5)-4a2;
解:原式=(a2+1+2a)(a2+1-2a)
=(a+1)2(a-1)2.
(6)(2x+y)2-2(2x+y)(x-2y)+(x-2y)2.
解:原式=[2x+y-(x-2y)]2
=(x+3y)2.
6.计算:40×3.152+80×3.15×1.85+40×1.852.
解:原式=40×(3.152+2×3.15×1.85+1.852)
=40×(3.15+1.85)2
=40×25
=1000.
7.阅读材料:
例:求代数式y2+4y+8的最小值.
解:∵y2+4y+8=(y2+4y+4)+4=(y+2)2+4≥4,
∴当y=-2时,代数式y2+4y+8有最小值,最小值是4.
仿照例题,解决下列问题:
(1)求代数式m2+2m+3的最小值;
解:(1)m2+2m+3
=(m2+2m+1)+2
=(m+1)2+2≥2,
∴当m=-1时,代数式m2+2m+3有最小值,最小值是2;
(2)求代数式-m2+3m+的最大值.
解:(2)-m2+3m+
=-++
=-+3≤3,
∴当m=时,代数式-m2+3m+有最大值,最大值是3.
一、填空题
8.(1)设a、b为整数,且a2-2a+b2+6b=-10,则(b+1)a的值为 -2 ;
(2)已知实数x满足x+=3,则的值为 ;
(3)若x=+1,则(x+1)2-4(x+1)+4的值为 2 .
-2
2
二、解答题
9.分解因式:
(1)a2-b2-2a+2b;
解:原式=(a+b)(a-b)-2(a-b)
=(a-b)(a+b-2).
(2)m2-25+9n2+6mn;
解:原式=(m2+6mn+9n2)-25
=(m+3n)2-25
=(m+3n+5)(m+3n-5).
(3)(a+c)(a-c)+b(b+2a).
解:原式=a2-c2+b2+2ab
=a2+2ab+b2-c2
=(a+b)2-c2
=(a+b+c)(a+b-c).
10.若x+y=2,y-z=-1,求代数式x2+y2+z2+xy-yz+xz的值.
解:∵x+y=2,y-z=-1,
∴x+z=3,
x2+y2+z2+xy-yz+xz
=(2x2+2y2+2z2+2xy-2yz+2xz)
=[(x+y)2+(y-z)2+(x+z)2]
=[22+(-1)2+32]
=7.
解答题
11.阅读材料:
例:若x满足(210-x)(x-200)=-204,试求(210-x)2+(x-200)2的值.
解:设210-x=a,x-200=b,
则ab=-204且a+b=210-x+x-200=10,
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2-2ab=102-2×(-204)=508,
即(210-x)2+(x-200)2的值为508.
仿照例题,解决问题:
若x满足(300-x)2+(302-x)2=512,试求(300-x)(302-x)的值.
解:设302-x=a,300-x=b,
∴a-b=2,
∵(a-b)2=a2-2ab+b2,a2+b2=512,
∴ab=[a2+b2-(a-b)2]=254,
即(300-x)(302-x)的值为254.
谢 谢 观 看
第18课时 十字相乘法
第十四章 整式的乘法与因式分解
一、选择题
1.对x2-3x+2分解因式,结果为( B )
A.x(x-3)+2 B.(x-1)(x-2)
C.(x-1)(x+2) D.(x+1)(x-2)
2.若多项式x2-mx+24可以分解因式,则整数m可取的值共有( D )
A.4个 B.6个 C.7个 D.8个
B
D
二、填空题
3.分解因式:
(1)ax2+2ax-3a= a(x+3)(x-1) ;
(2)(a+2)(a-2)+3a= (a-1)(a+4) ;
(3)x2-4x-12= (x-6)(x+2) ;
(4)3x2+3x-6= 3(x+2)(x-1) ;
(5)2x2-3x+1= (2x-1)(x-1) .
a(x+3)(x-1)
(a-1)(a+4)
(x-6)(x+2)
3(x+2)(x-1)
(2x-1)(x-1)
三、解答题
4.分解因式:
(1)x2-2x-15; (2)x2-10x-24;
解:原式=(x-5)(x+3)
解:原式=(x-12)(x+2)
(3)a2-15a+36; (4)x2-5xy+6y2;
解:原式=(a-12)(a-3)
解:原式=(x-2y)(x-3y)
(7)-ax2+4ax+5a.
解:原式=-a(x2-4x-5)
=-a(x-5)(x+1).
(5)x2+8xy-33y2; (6)(x+1)(x+3)-15;
解:原式=(x+11y)(x-3y)
解:原式=x2+4x+3-15
=x2+4x-12
=(x+6)(x-2).
5.把下列各式分解因式:
(1)5x2+7x-6;
解:原式=(5x-3)(x+2).
(2)3x2-7x+2;
解:原式=(3x-1)(x-2).
(3)10x2-17x+3;
解:原式=(5x-1)(2x-3).
(4)-6y2+11y+10;
解:原式=-(3y+2)(2y-5).
(5)2x2-7xy+6y2;
解:原式=(x-2y)(2x-3y).
(6)6x4-7x2+2.
解:原式=(2x2-1)(3x2-2).
一、填空题
6.若3x2+8xy-3y2=0,则代数式的值为 或-3 .
7.若x-2是x2+kx-14的一个因式,则k= 5 .
8.若x2-y2+kx+5y-6能分解为两个一次因式的积,则k的值为 ±1 .
或-3
5
±1
二、解答题
9.把下列各式分解因式:
(1)x4-10x2+9;
解:原式=(x2-1)(x2-9)
=(x+1)(x-1)(x+3)(x-3).
(2)7(x+y)3-5(x+y)2-2(x+y);
解:原式=(x+y)(7x+7y+2)(x+y-1).
(3)+22(a2+8a)+120;
解:原式=(a2+8a+12)(a2+8a+10)
=(a+2)(a+6)(a2+8a+10).
(4)(x2+2x-3)(x2+2x-24)+90;
解:原式=(x2+2x)2-27(x2+2x)+72+90
=(x2+2x)2-27(x2+2x)+162
=(x2+2x-9)(x2+2x-18).
(5)x(x+1)(x+2)(x+3)-8.
解:原式=(x2+3x)(x2+3x+2)-8
=(x2+3x)2+2(x2+3x)-8
=(x2+3x+4)(x2+3x-2).
解答题
10.阅读材料:
“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的关于x,y的二次三项式来说,方法的关键是把含x2的项的系数a分解成两个因数a1,a2的积,即a=a1a2,把含y2的项的系数c分解成两个因数c1,c2的积,即c=c1c2,并使a1c2+a2c1正好等于含xy的项的系数b,那么可以直接写出结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
解:如图1,其中1=1×1,-8=(-4)×2,而-2=1×2+1×(-4),
∴x2-2xy-8y2=(x-4y)(x+2y).
第10题图1
例:分解因式:x2-2xy-8y2.
而对于形如ax2+bxy+cy2+dx+ey+f的关于x,y的二元二次式也可以用十字相乘法来分解,如图2,把a分解成两个因数m,n作为第1列,c分解成两个因数p,q作为第2列,f分解成两个因数j,k作为第3列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,那么原式=(mx+py+j)(nx+qy+k).
第10题图2
例:分解因式:x2+2xy-3y2+3x+y+2.
解:如图3,其中1=1×1,-3=(-1)×3,2=1×2,
而2=1×3+1×(-1),1=(-1)×2+3×1,3=1×2+1×1,
∴x2+2xy-3y2+3x+y+2=(x-y+1)(x+3y+2).
第10题图3
请同学们通过上述材料,完成下列问题:
(1)分解因式:
(i)6x2-17xy+12y2= ;
(ii)2x2-xy-6y2+2x+17y-12= ;
(iii)x2-xy-6y2+2x-6y= .
(3x-4y)(2x-3y)
(x-2y+3)(2x+3y-4)
(x-3y)(x+2y+2)
(2)若关于x,y的二元二次式x2+7xy-18y2-5x+my-24可以分解成两个一次因式的积,求m的值.
或
解:(2)如图,
∴m=3×9+(-8)×(-2)=43或m=9×(-8)+3×(-2)=-78,
∴m的值为43或-78.
或
谢 谢 观 看
第19课时 复习巩固
第十四章 整式的乘法与因式分解
一、选择题
1.下列运算正确的是( D )
A.a2·a3=a6
B.(a2)3=a5
C.a6÷a2=a3
D.(a+2b)(a-2b)=a2-4b2
2.若(x-3)(x+a)=x2+bx-15,则ab的值为( A )
A.25 B.5 C.32 D.-25
D
A
3.已知3a=1,3b=2,则3a+b的值为( B )
A.1 B.2 C.3 D.27
4.若x+y=2,则多项式x2+2xy+2y2的值为( C )
A.2 B.4 C.8 D.16
5.计算52022×的结果是( C )
A.5 B.-5 C.- D.
B
C
C
二、填空题
6.(1)已知a+=5,则a2+= 23 ;
(2)若2m=a,8n=b,m、n为正整数,则23m+9n= a3b3 ;
(3)若x2+x-1=0,则代数式x3+2x2-7的值是 -6 .
23
a3b3
-6
三、解答题
7.计算:
(1)x3·xn-1-xn-2·x4+xn+2;
解:原式=xn+2-xn-2+4+xn+2
=xn+2.
(2)(m-n)2·(n-m)2÷(n-m)3;
解:原式=(n-m)4÷(n-m)3
=n-m.
(3)(x+1)2-(x-1)(x+2).
解:原式=(x2+2x+1)-(x2+x-2)
=x+3.
8.解答下列各题:
(1)已知(a+b)2=7,(a-b)2=4,求ab的值;
解:∵(a+b)2=7,(a-b)2=4,
∴ab=×[(a+b)2-(a-b)2]
=×3
=.
(2)化简求值:[4(x2+y)(x2-y)-(2x2-y)2]÷y,其中x=,y=3.
解:原式=(4x4-4y2-4x4+4x2y-y2)÷y
=(-5y2+4x2y)÷y
=-5y+4x2,
当x=,y=3时,
原式=-15+1=-14.
9.分解因式:
(1)m3(x-2)+m(2-x);
解:原式=m3(x-2)-m(x-2)
=m(x-2)(m2-1)
=m(x-2)(m+1)(m-1).
(2)25(x+y)2-36(x-y)2.
解:原式=[5(x+y)]2-[6(x-y)]2
=(5x+5y+6x-6y)(5x+5y-6x+6y)
=(11x-y)(11y-x).
一、填空题
10.我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=,则h(2)= ;
(2)如果h(1)=k(k≠0),那么h(n)·h(2023)= kn+2023 .(用含n和k的代数式表示,其中n为正整数)
11.若a=x+2021,b=x+2022,c=x+2023,则代数式2(a2+b2+c2-ab-bc-ac)的值是 6 .
kn+2023
6
二、解答题
12.已知(x-y)2=9,x2+y2=5,求[x(x2y2-xy)-y(x2-x3y)]÷x2y的值.
解:∵(x-y)2=x2+y2-2xy=9,x2+y2=5,
∴2xy=-4,即xy=-2,
∴原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y
=2(xy-1)
=-6.
13.以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)已知(x+3)2(x2+mx+n)既不含二次项,也不含一次项,求m+n的值;
解:(1)原式=(x2+6x+9)(x2+mx+n)
=x4+(m+6)x3+(6m+n+9)x2+(9m+6n)x+9n,
∵既不含二次项,也不含一次项,
∴6m+n+9=0,9m+6n=0,
解得:m=-2,n=3,
∴m+n=1;
(2)多项式M与多项式x2-3x+1的乘积为2x4+ax3+bx2+cx-3,求2a+b+c的值.
解:(2)∵多项式M与多项式x2-3x+1的乘积为2x4+ax3+bx2+cx-3,
∴设多项式M=2x2+px-3,
∴(2x2+px-3)(x2-3x+1)
=2x4-6x3+2x2+px3-3px2+px-3x2+9x-3
=2x4+(p-6)x3+(2-3p-3)x2+(p+9)x-3
=2x4+ax3+bx2+cx-3,
∴a=p-6,b=-3p-1,c=p+9,
∴2a+b+c=2p-12-3p-1+p+9=-4.
解答题
14.1261年,我国宋代数学家杨辉写了一本书《详解九章算法》,书中记载了一个用数字排成的三角形我们叫做杨辉三角(如图).
(1)请写出第五行的数字为 ;
解:(1)由规律可得出第五行的数字为1、5、10、10、5、1
第14题图
1、5、10、10、5、1
(2)第n行杨辉三角数字与(a+b)n的展开结果关系如图所示,请写出(a+b)5的展开结果;
解:(2)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
第14题图
(3)已知(a-b)1=a-b,(a-b)2=a2-2ab+b2,(a-b)3=a3-3a2b+3ab2-b3,(a-b)4=a4-4a3b+6a2b2-4ab3+b4,请写出(a-b)5的展开结果.
解:(3)(a-b)5=a5-5a4b+10a3b2-10a2b3+5ab4-b5.
谢 谢 观 看
第1课时 同底数幂的乘法
第十四章 整式的乘法与因式分解
一、选择题
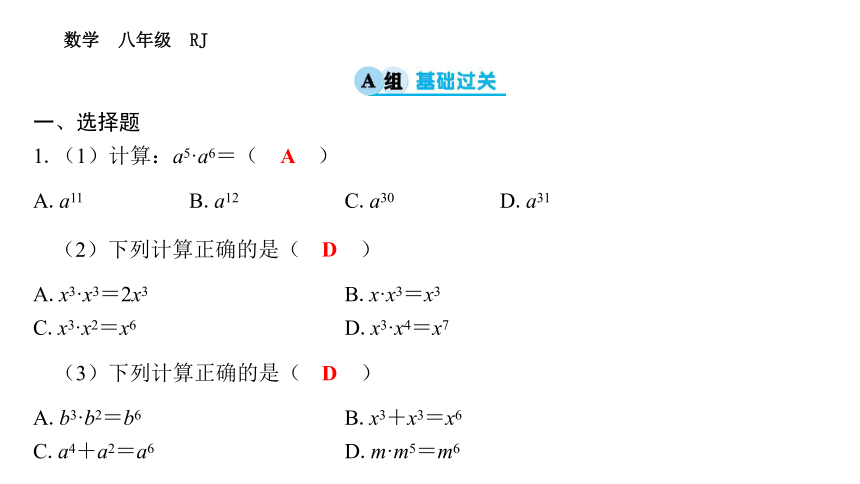
1.(1)计算:a5·a6=( A )
A.a11 B.a12 C.a30 D.a31
(2)下列计算正确的是( D )
A.x3·x3=2x3 B.x·x3=x3
C.x3·x2=x6 D.x3·x4=x7
(3)下列计算正确的是( D )
A.b3·b2=b6 B.x3+x3=x6
C.a4+a2=a6 D.m·m5=m6
A
D
D
2.计算-(-m2)·(-m)3·(-m)的正确结果是( C )
A.-m3 B.m5 C.m6 D.-m6
3.(1)已知2m=1,2n=3,则2m+n=( B )
A.2 B.3 C.4 D.6
(2)已知x+y-3=0,则2x·2y的值为( B )
A.64 B.8 C.6 D.12
C
B
B
二、填空题
4.计算:
(1)2×22×23= 26 ;
(2)10m+1×10n-1= 10m+n ;
(3)(-x)3·(-x)2= -x5 ;
(4)(m-n)·(m-n)2·(m-n)3= (m-n)6 ;
(5)(x-y)·(y-x)3= -(x-y)4 .
5.若a4·=a11,则m= 4 .
26
10m+n
-x5
(m-n)6
-(x-y)4
4
三、解答题
6.计算:
(1)(-x)(-x3)(-x3)(-x4);
解:原式=x4·x7
=x11.
(2)(-a2)·(-a)3;
解:原式=(-a2)·(-a3)
=a2+3
=a5.
(3)(x-2y)2(x-2y)3.
解:原式=(x-2y)2+3
=(x-2y)5.
7.计算下列各题:
(1)(a-b)3·(a-b)2·(b-a)5;
解:原式=(a-b)5·[-(a-b)5]
=-(a-b)10.
(2)a2·a3-(-a3)·a4+a6·(-a);
解:原式=a5+a7-a7
=a5.
(3)(m-n)2(n-m)3(m-n)6.
解:原式=(n-m)2(n-m)3(n-m)6
=(n-m)2+3+6
=(n-m)11.
8.(1)若ax+3=a2x+1(a≠0,a≠1),求x的值;
解:由题意得x+3=2x+1,
则x=2.
(2)若px·p6=p2x(p≠0,p≠1),求x的值;
解:由题意得px+6=p2x,
∴x+6=2x,则x=6.
(3)若an+1·am+n=a6(a≠0且a≠1),且2m=8,求mn的值.
解:由题意得,an+1·am+n=am+2n+1=a6,
则m+2n=5,
∵2m=8=23,∴m=3,
∴3+2n=5,∴n=1,
故mn=3.
一、填空题
9.已知x·xm·xn=x14(x≠0,x≠1),且m比n大3,则mn的值为 40 .
10.已知10α=3,10β=5,10γ=7,试把105写成底数是10的幂的形式是 10α+β+γ .
40
10α+β+γ
二、解答题
11.(1)若2a+5=9,求3×2a+4的值;
解:∵2a+5=9,
∴2a+4×2=9,
∴2a+4=,
则3×2a+4=3×=.
(2)已知a+b+c=3,求22a-3·23b-2·2a+3c的值.
解:22a-3·23b-2·2a+3c
=22a-3+3b-2+a+3c
=23(a+b+c)-5,
∵a+b+c=3,
∴原式=23×3-5=24=16.
12.规定运算:a*b=2a×2b.
(1)求2*3的值;
解:(1)∵a*b=2a×2b,
(2)若2*(x+1)=16,求x的值.
∴2*3=22×23=4×8=32;
解:(2)∵2*(x+1)=16,
∴22·2x+1=24,即22+x+1=24,
∴2+x+1=4,
解得:x=1.
解答题
13.记M(1)=-2,
M(2)=(-2)×(-2),
M(3)=(-2)×(-2)×(-2),
…,
M(n)=.
(1)计算:M(5)+M(6);
(2)求2M(2023)+M(2024)的值;
(3)说明2M(n)与M(n+1)互为相反数.
解:(1)M(5)+M(6)
=(-2)5+(-2)6
=-32+64=32;
(2)2M(2023)+M(2024)
=2×(-2)2023+(-2)2024
=-22024+22024=0;
(3)2M(n)+M(n+1)
=2·(-2)n+(-2)n+1
=(-2)n(2-2)=0,
∴2M(n)与M(n+1)互为相反数.
谢 谢 观 看
第2课时 幂的乘方
第十四章 整式的乘法与因式分解
一、选择题
1.计算:(-a4)2=( C )
A.2 B.-4 C. D.-a8
2.下列各式运算正确的是( D )
A.a3+a3= B.x3·x2=x6
C.(a3)2= D.(-a2)3=-a6
3.下列各式运算正确的是( B )
A.(x4)3=x7 B.(am)2=a2m
C.[(-a)2]5=-a10 D.(-a3)2=-a6
C
D
B
4.下列计算结果是a9的是( A )
A.a3·a6 B.(a3)6
C.a3+a6 D.a9+a9
A
二、解答题
5.计算:
(1)(102)3; (2)-(a2)4;
解:原式=106;
解:原式=-a8.
(3)(x3)5·x3; (4)[(-x)2]3;
解:原式=x15·x3=x18;
解:原式=x6.
(5)(-a)2(a2)2;
解:原式=a6;
(6)x·(-x2)2-x2·x3.
解:原式=x5-x5
=0.
6.计算:
(1)x2·x5·x+4(-x4)2+(x2)4;
解:原式=x8+4x8+x8
=6x8.
(2)9(x3)2-x2·x4-(x2)3;
解:原式=9x6-x6-x6
=7x6.
(3)a3·a·a4+7(a4)2+(-a2)4;
解:原式=a8+7a8+a8
=9a8.
(4)(-a)3·a2-(-a)2·(-a3).
解:原式=-a5+a2·a3
=0.
7.解方程:
(1)23x-1·22-x=2x+2;
解:∵23x-1·22-x=2x+2,
∴3x-1+2-x=x+2,
解得x=1.
(2)3x·92x=910.
解:∵3x·92x=910,
∴3x·34x=320,
∴x+4x=20,
解得x=4.
一、选择题
8.若x,y均为正整数,且2x·4y=32,则x+2y的值为( C )
A.3 B.4 C.5 D.6
C
二、填空题
9.已知am=3,a2m+n=45,则an= 5 .
10.已知27b=9×3a+3,16=4×22b-2,则a+b的值为 3 .
5
3
三、解答题
11.已知n为正整数,且x2n=4,求9(x3n)2-13(x2)2n的值.
解:∵x2n=4,
∴9(x3n)2-13(x2)2n
=9(x2n)3-13(x2n)2
=9×43-13×42
=368.
12.解答下列问题:
(1)已知3m=5,3n=2,求33m+2n+1的值;
解:∵3m=5,3n=2,
∴原式=(3m)3·(3n)2×3
=53×22×3
=125×4×3
=1500.
(2)若3x+4y-3=0,求27x·81y的值;
解:∵3x+4y-3=0,
∴3x+4y=3,
∴原式=33x·34y
=33x+4y
=33
=27.
(3)已知16m=4×22n-2,27n=9×3m+3,求(m-n)2024的值.
解:∵16m=4×22n-2,27n=9×3m+3,
∴24m=22×22n-2,33n=32×3m+3,
则4m=2+2n-2,3n=2+m+3,
解得:m=1,n=2,
则(m-n)2024=1.
13.比较大小:
(1)比较2100与375的大小;
解:∵2100=(24)25=1625,
375=(33)25=2725,
而16<27,
∴1625<2725,
∴2100<375.
(2)比较344、433、522的大小;
解:∵344=(34)11=8111,
433=(43)11=6411,
522=(52)11=2511,
而81>64>25,
∴8111>6411>2511,
即344>433>522.
(3)已知a2=2,b3=3,比较a、b的大小.
解:由b3=3可得b>0,
当a<0时,a<b;
当a>0时,a6=8,b6=9,
∵8<9,
∴a6<b6,
∴a<b,
综上所述,a<b.
解答题
14.若2a=2,4b=6,8c=12,试求a,b,c的数量关系.
解:∵4b=6,∴22b=6,
∵8c=12,∴23c=12,
∴2a·22b=2×6=12,
即2a+2b=12,
∴2a+2b=23c,
∴a+2b=3c.
谢 谢 观 看
第3课时 积的乘方
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算的结果是( C )
A.6x6 B.8x27 C.8x9 D.6x
(2)计算的结果是( C )
A.m6n B.m5n2 C.m6n2 D.m3n2
(3)计算的结果是( B )
A.-m5n B.-m6n3
C.m6n3 D.-m5n3
C
C
B
2.(1)下列计算正确的是( C )
A.x2·x4=x8 B.=x5
C.x2+x2=2x2 D.(3x)2=3x2
(2)下列运算中,正确的是( A )
A.=16x4y6
B.-=12x2y6
C.=-9x9y
D.(-x)3·x2·(-x)=x5
C
A
3.(1)计算:2200×=( A )
A.1 B.-1 C.2400 D.-2400
(2)计算:(-4)2023×=( D )
A.4 B.-4 C. D.-
4.已知xa=2,xb=4,则x2a+b的值是( D )
A.2 B.6 C.8 D.16
A
D
D
二、填空题
5.若(a3·ax)2=a20,则x的值为 7 .
6.计算:·= - .
7.计算:(1)-= -x3y6 ;
(2)(-a3)4+(-2a2)3= a12-8a6 .
7
-
-x3y6
a12-8a6
三、解答题
8.计算:
(1)(-5b)3;
解:原式=-125b3.
(2)-;
解:原式=-a4b6.
(3).
解:原式=a4b2.
9.计算:
(1)(-a3b6)2-(-a2b4)3-2a4b2·(ab5)2;
解:原式=a6b12+a6b12-2a4b2·a2b10
=2a6b12-2a6b12
=0.
(2)a3·a·a4+(-2a4)2+(a2)4;
解:原式=a8+4a8+a8
=6a8.
(3)(2a2)3+(-3a3)2+(a2)2·a2;
解:原式=8a6+9a6+a4·a2
=8a6+9a6+a6
=18a6.
(4)m·m5+(-2m3)2-4(m2)3;
解:原式=m6+4m6-4m6
=m6.
(5)××.
解:原式=×××
=××
=-1××
=-.
一、填空题
10.(1)计算:×41010= ;
(2)计算:[a(a-b)2]3·[a2(b-a)3]2= a7(a-b)12 ;
(3)如果=a9b12,那么m+n= 7 ;
(4)已知an=-1,b2n=3,则(-a2b)4n的值为 9 ;
(5)已知3m·9m·27m·81m=330,则m的值为 3 .
11.有一个棱长10cm的正方体,在某种物质的作用下,棱长每秒扩大到之前的102倍,则3秒后该正方体的体积是 1021 cm3.
a7(a-b)12
7
9
3
1021
二、解答题
12.(1)已知2x+5y-3=0,求4x·32y的值;
解:∵2x+5y-3=0,
∴2x+5y=3,
则原式=(22)x·(25)y
=22x·25y
=22x+5y
=23
=8.
(2)已知25m·2·10n=57·24,求m,n的值.
解:25m·2·10n=52m·2·(2×5)n
=52m+n·2n+1,
∵25m·2·10n=57·24,
∴52m+n·2n+1=57·24,
则,解得,
∴m的值为2,n的值为3.
13.计算下列各题:
(1)0.1259×(-8)10+×(2)12;
解:原式=(0.125×8)9×8+×
=1×8+1×
=.
(2)an-5·(an+1b3m-2)2+(an-1bm-2)3·(-b3m+2).
解:原式=an-5·(a2n+2b6m-4)+(a3n-3b3m-6)·(-b3m+2)
=a3n-3b6m-4-a3n-3b6m-4
=0.
解答题
14.若am=an(a>0且a≠1,m、n是正整数),则m=n.
试利用上述结论分别求下列各方程中x的值:
(1)2×8x=27;
解:(1)原方程可化为2×23x=27,
∴23x+1=27,
∴3x+1=7,
解得x=2;
(2)2x+1×3x+1=36x-2;
解:(2)原方程可化为(2×3)x+1=36x-2,
∴6x+1=62(x-2),
∴x+1=2(x-2),
解得x=5;
(3)2x+2+2x+1=24.
解:(3)原方程可化为2×2x+1+2x+1=24,
∴3×2x+1=3×8,
∴2x+1=8=23,
∴x+1=3,
解得x=2.
谢 谢 观 看
第4课时 整式的乘法(1)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算6x2·x3的结果是( B )
A.6x B.6x5 C.6x6 D.6x9
(2)计算(2x)3·(-x2)的结果为( C )
A.8x6 B.-2x5 C.-8x5 D.2x5
(3)计算:(-2x2y3)·3xy2=( B )
A.-6x2y6 B.-6x3y5
C.-5x3y5 D.-24x7y5
B
C
B
2.下列运算正确的是( D )
A.4x+5y=9xy B.2a3·a3=8a6
C.a2·a3=a6 D.(-ab)4=a4b4
3.若( )·(-xy)2=4x2y3,则括号里应填的单项式是( A )
A.4y B.-4y C.4xy D.-2xy
D
A
二、填空题
4.计算:(1)(-2x2)·3x4= -6x6 ;
(2)-4a3b2c·3ab3= -12a4b5c ;
(3)(3×105)×(8×105)= 2.4×1011 .(结果用科学记数法表示)
5.计算:3xmy3·(-2xym+1)= -6xm+1ym+4 .(m是正整数)
6.(1)已知3x3y·★=12x5y,则“★”所表示的式子是 4x2 ;
(2)若5am+1b2与3an+2bn的积是15a8b4,则nm= 8 .
-6x6
-12a4b5c
2.4×1011
-6xm+1ym+4
4x2
8
三、解答题
7.计算:
(1)·;
解:原式=-×a3bc2
=-a3bc2.
(2)·(-3xy);
解:原式=4x4y2·(-3xy)
=-12x5y3.
(3)(5×105)×(3×102).
解:原式=1.5×108.
8.计算下列各题:
(1)2x7·(-x3)-(-x3)2·x4;
解:原式=-2x10-x6·x4
=-2x10-x10
=-3x10.
(2)(-2x2y)3+(3x)2·(-x)4·y3;
解:原式=-8x6y3+9x2·x4y3
=-8x6y3+9x6y3
=x6y3.
(3)(-3a3)2·a3+(-4a2)·a7-(5a3)3;
解:原式=9a6·a3-4a2·a7-125a9
=9a9-4a9-125a9
=-120a9.
(4)先化简,再求值:(-2a2b3)(-ab2)2+·4b,其中a=2,b=1.
解:原式=-2a2b3·a2b4+a4b6·4b
=-2a4b7+a4b7
=-a4b7,
当a=2,b=1时,
原式=-24×1=-16.
一、选择题
9.计算2x·(-3xy)2·(-x2y)3的结果是( C )
A.18x8y5 B.6x9y5
C.-18x9y5 D.-6x4y5
C
二、填空题
10.(1)若2a3y2·(-4a2y3)=ma5yn,则m+n的值为 -3 ;
(2)若-5am+1·b2n-1·2ab2=-10a4b4,则m-n的值为 ;
(3)如果单项式-3x2a-by2与x3a+by5a+8b是同类项,那么这两个单项式的积是 10y4 .
-3
-x10y4
三、解答题
11.成都市环保局将一个长为2×106分米,宽为4×104分米,高为8×102分米的长方体废水池中的满池废水注入正方体贮水池净化,那么请你想一想,能否恰好有一个正方体贮水池将这些废水刚好装满?若有,求出正方体贮水池的棱长;若没有,请说明理由.
解:有,
∵长方体废水池的容积为:
(2×106)×(4×104)×(8×102)
=64×1012
=43×(104)3
=(4×104)3立方分米,
∴正方体水池的棱长为4×104分米.
解答题
12.解答下列各题:
(1)已知(2x3y2)·(-3xmy3)·(5x2yn)=-30x4y2,求m+n的值;
解:∵(2x3y2)·(-3xmy3)·(5x2yn)
=-30xm+5yn+5=-30x4y2,
∴m+5=4,n+5=2,即m=-1,n=-3,
则m+n=-4.
(2)若[-3(x+y)m(x-y)2n]2·[-(x+y)2]=-9(x+y)10(x-y)10-n,
求(m-n)3的值;
解:∵[-3(x+y)m(x-y)2n]2·[-(x+y)2]
=-9(x+y)2m+2(x-y)4n
=-9(x+y)10(x-y)10-n,
∴2m+2=10,4n=10-n,
∴m=4,n=2,
当m=4,n=2时,
(m-n)3=×(4-2)3=2.
(3)已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的平方根.
解:(-2x3m+1y2n)·(7xn-6y-3-m)
=-14x(3m+1)+(n-6)y2n+(-3-m)
=-14x3m+n-5y2n-m-3,
∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴,解得,
∴m2+n=7,
∴m2+n的平方根是±.
谢 谢 观 看
第5课时 整式的乘法(2)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算:x(x2-1)=( B )
A.x3-1 B.x3-x
C.x3+x D.x2-x
(2)把2a(ab-b+c)化简后得( D )
A.2a2b-ab+ac B.2a2-2ab+2ac
C.2a2b+2ab+2ac D.2a2b-2ab+2ac
B
D
(3)化简:(-3s+t)·(-7st2)=( B )
A.21s2t2-14st3 B.21s2t2-st3
C.-21s2t2+14st3 D.-21s2t2+st
B
2.已知x2-4x-1=0,则代数式x(x-4)+1的值为( A )
A.2 B.1 C.0 D.-1
3.某同学在计算-3x2乘一个多项式时错误的计算成了加法,得到的答案是x2-x+1,由此可以推断正确的计算结果是( C )
A.4x2-x+1 B.x2-x+1
C.-12x4+3x3-3x2 D.无法确定
A
C
二、填空题
4.计算:xm·(2xm-4x2-8y)= 2x2m-4xm+2-8xmy .(m为正整数)
5.(1)若(x2-a)x+2x的展开式中只含有x3这一项,则a的值是 2 ;
(2)若3x(x+1)=mx2+nx,则m+n= 6 .
2x2m-4xm+2-8xmy
2
6
三、解答题
6.计算:
(1)2ab2·(3a2b-2ab-1);
解:原式=6a3b3-4a2b3-2ab2.
(2)-3x·.
解:原式=-x3y3-6xy2+3x.
7.计算:
(1)2x-3x;
解:原式=x2-2x-x2+5x
=3x.
(2)2x(-x2+3x-4)+3x2;
解:原式=-2x3+6x2-8x+x3+3x2
=-x3+9x2-8x.
(3)3a·(a2+2a)-2a2(a-3).
解:原式=3a3+6a2-2a3+6a2
=a3+12a2.
8.解方程:2x(x+1)-(3x-2)x=1-x2.
解:去括号,得2x2+2x-3x2+2x=1-x2,
整理,得4x=1,
解得x=.
(2)当x=2时,先化简:A+B,再求其值.
解:(2)A+B=x+(6x2-4x-2)
=6x2-x-2,
当x=2时,
原式=6×22-×2-2=15.
9.已知A=x,B是多项式,王虎同学在计算A+B 时,误把A+B看成了A×B,结果得3x3-2x2-x.
(1)求多项式B;
解:(1)由题意可知:x·B=3x3-2x2-x,
∴B=6x2-4x-2;
一、选择题
10.(1)下列各式中,计算正确的有( B )
①(a-3b)(-6a)=-6a2+18ab;
②(-9xy+2)=3x3y2+2;
③(-4ab)=2a3b2;
④=ab2-2ab.
B
A.1个 B.2个 C.3个 D.4个
(2)已知a-b=3,b-c=-2,则代数式a2-ac-b(a-c)的值为( C )
A.4 B.-4 C.3 D.-3
C
二、填空题
11.若(mx2-nx+2)·(-2x2)-4x3的结果中不含x4和x3的项,则m= 0 ,n= 2 .
12.通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据如图所示的图形写出一个代数恒等式: 2a(a+b)=2a2+2ab .
第12题图
0
2
2a(a+b)=2a2+2ab
三、解答题
13.已知有理数a、b、c满足|a-b-3|+(b+1)2+|c-1|=0,求(-3ab)(a2c-6b2c)的值.
解:由|a-b-3|+(b+1)2+|c-1|=0,
得:,解得:,
∵(-3ab)(a2c-6b2c)=-3a3bc+18ab3c,
∴当a=2,b=-1,c=1时,
原式=-3×23×(-1)×1+18×2×(-1)3×1
=24-36
=-12.
14.已知ab=3,求(2a3b2-3a2b+4a)(-2b)的值.
解:(2a3b2-3a2b+4a)(-2b)
=-4a3b3+6a2b2-8ab
=-4(ab)3+6(ab)2-8ab
=-4×33+6×32-8×3
=-108+54-24
=-78.
解答题
15.若m2+m-1=0,求代数式m3+2m2+2023的值.
解:∵m2+m-1=0,
∴m2+m=1,m2=1-m,
∴m3+2m2+2023
=m(1-m)+2m2+2023
=m-m2+2m2+2023
=m2+m+2023
=2024.
谢 谢 观 看
第6课时 整式的乘法(3)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算(x+1)(x-2)的结果是( B )
A.x2+x-2 B.x2-x-2
C.x2+2 D.x2-2
(2)计算(x+1)(2x-5)的结果是( A )
A.2x2-3x-5 B.2x2-6x-5
C.2x2-3x+5 D.x2-3x-5
B
A
(3)计算:(3m+5)(-3m-5)=( C )
A.9m2-25
B.-9m2-25
C.-9m2-30m-25
D.-9m2+30m-25
C
2.(1)若(x+2)(x+a)=x2-bx-8,则ab的值为( D )
A.-8 B.-4 C. D.16
(2)将多项式(x2+x-3)(x2-2x+2a)展开,常数项为-30,则a=( C )
A.3 B.4 C.5 D.6
(3)若(x+1)(2x2-ax+1)的运算结果中,x2的系数为-6,则a的值是( C )
A.4 B.-4 C.8 D.-8
(4)要使多项式(x+p)(x-q)不含x的一次项,则p与q的关系是( A )
A.相等 B.互为相反数
C.互为倒数 D.乘积为-1
D
C
C
A
二、填空题
3.计算:(5m+2)(2m-1)= 10m2-m-2 .
4.若(x+a)(x+b)=x2+6x+5,则a+b的值为 6 .
5.已知三角形的底边是(6a+2b)cm,高是(2b-3a)cm,则这个三角形的面积是 (-9a2+3ab+2b2) cm2.
10m2-m-2
6
(-9a2+3ab+2b2)
三、解答题
6.计算:
(1)(a+1)(a-6);
解:原式=a2-6a+a-6
=a2-5a-6.
(2)(2y+3)(y-1);
解:原式=2y2-2y+3y-3
=2y2+y-3.
(3)(m+2n)(2m-n);
解:原式=2m2-mn+4mn-2n2
=2m2+3mn-2n2.
(4)(x+3y-4)(2x-y).
解:原式=2x2-xy+6xy-3y2-8x+4y
=2x2+5xy-3y2-8x+4y.
7.计算下列各题:
(1)6x(x2+2)-x(3x-2)(2x-3);
解:原式=6x3+12x-(3x2-2x)(2x-3)
=6x3+12x-(6x3-9x2-4x2+6x)
=6x3+12x-6x3+9x2+4x2-6x
=13x2+6x.
(2)(3y+2)(y-4)-(y-2)(y-3).
解:原式=3y2+2y-12y-8-(y2-5y+6)
=3y2-10y-8-y2+5y-6
=2y2-5y-14.
8.已知A=1+2x,B=1-2x+4x2,C=1-4x3.
(1)化简:A·B-C;
解:(1)∵A=1+2x,B=1-2x+4x2,C=1-4x3,
∴A·B-C
=(1+2x)(1-2x+4x2)-1+4x3
=1-2x+4x2+2x-4x2+8x3-1+4x3
=12x3;
(2)当x=-时,求A·B-C的值.
解:(2)由(1)得A·B-C=12x3,
当x=-时,
原式=12×(-)3=-.
一、选择题
9.若不管a取何值,多项式a3+2a2-a-2与(a2-ma+2n)(a+1)都相等,则m,n的值分别为( A )
A.-1,-1 B.-1,1
C.1,-1 D.1,1
A
二、填空题
10.如图,现有正方形卡片A类、B类和长方形卡片C类各若干张(a≠b),若要选用上述3类卡片共12张拼成一个大长方形(拼接时不可重叠,不可有缝隙),且卡片全部用上,则拼成的大长方形有 11 种.
第10题图
11
三、解答题
11.若(x2+px+8)(x2-3x-q)的展开式中不含x3和x2的项,求2p+q的值.
解:(x2+px+8)(x2-3x-q)
=x4-3x3-qx2+px3-3px2-pqx+8x2-24x-8q
=x4+(-3+p)x3+(-q-3p+8)x2+(-pq-24)x-8q,
∵展开式中不含x3和x2的项,
∴,
解得:p=3,q=-1,
∴2p+q=6-1=5.
解答题
12.你能化简(x-1)(x99+x98+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,然后归纳出一些方法.
(1)分别化简下列各式:
(x-1)(x+1)= ;
(x-1)(x2+x+1)= ;
(x-1)(x3+x2+x+1)= ;
…,
(x-1)(x99+x98+…+x+1)= .
解:(1)(x-1)(x+1)=x2+x-x-1=x2-1;
(x-1)(x2+x+1)=x3+x2+x-x2-x-1=x3-1;
(x-1)(x3+x2+x+1)=x4+x3+x2+x-x3-x2-x-1=x4-1;
…,
(x-1)(x99+x98+…+x+1)=x100+x99+…+x2+x-(x99+x98+…+x+1)=x100-1,
故答案为:x2-1;x3-1;x4-1;x100-1;
(2)请你利用上面的结论计算:299+298+…+2+1.
解:(2)原式=(2-1)×(299+298+…+2+1)
=2100-1.
谢 谢 观 看
第7课时 整式的乘法(4)
第十四章 整式的乘法与因式分解
一、选择题
1.下列运算正确的是( C )
A.(a3)2=a5 B.a3·a2=a6
C.(ab)4=a4b4 D.a6÷a3=a2
2.下列各式的运算结果是x6的是( C )
A.x4+x2 B.x12÷x2 C.(x2)3 D.x2·x3
C
C
3.(1)计算:x5÷x2=( B )
A.x2 B.x3 C.2x D.x7
(2)计算(2xy2)3÷2xy2的结果是( D )
A.3 B.3xy2 C.8xy D.4x2y4
4.若2x=5,2y=3,则22x-y的值为( B )
A.25 B. C.9 D.75
B
D
B
二、填空题
5.计算:(-5)8·(-5)6÷(-5)12= 25 .
6.(1)若ax÷a3·a5=a6,则x= 4 ;
(2)已知a5=6,a2=2,则a3= 3 ;
(3)已知(3x+1)0=1,则x满足的条件是 x≠- .
25
4
3
x≠-
三、解答题
7.计算:
(1)÷y5;
解:原式=y6÷y5
=y.
(2)(-a2b4)8÷(-a2b4)2.
解:原式=(-a2b4)6
=a12b24.
8.计算下列各题:
(1)(-a2)3+a2·a3+a8÷(-a2);
解:原式=-a6+a5-a6
=-2a6+a5.
(2)x3·x6+x20÷x10-xn+8÷xn-1;
解:原式=x9+x10-x9
=x10.
(3)y4+(y2)4÷y4-(-y2)2;
解:原式=y4+y8÷y4-y4
=y4+y4-y4
=y4.
(4)x3·x5-(2x4)2+x10÷x2.
解:原式=x8-4x8+x8
=-2x8.
9.(1)已知2×8x×16=223,求x的值;
解:∵2×8x×16=223,
∴2×(23)x×24=223,
∴2×23x×24=223,
∴1+3x+4=23,
解得x=6.
①am+n的值;
②a3m-2n的值.
解:①am+n=am·an
=5×3=15;
②a3m-2n=a3m÷a2n
=(am)3÷(an)2
=33÷52
=.
(2)已知am=3,an=5,求:
一、填空题
10.(1)已知10a=20,10b=,则3a÷3b= 9 ;
(2)已知5x=6,5y=3,则5x+2y-1= ;
(3)已知25a·52b=56,4b÷4c=4,则代数式a2+ab+3c的值是 6 ;
(4)已知2m=4n-1,27n=3m-1,则n-m= 5 .
9
6
5
二、解答题
11.解答下列各题:
(1)若3x=4,3y=6,求92x-y+27x-y的值;
解:∵3x=4,3y=6,
∴92x-y+27x-y
=(32)2x-y+(33)x-y
=34x-2y+33x-3y
=(3x)4÷(3y)2+(3x)3÷(3y)3
=+
=.
(2)若26=a2=4b,求a+b的值.
解:26=(±23)2=(±8)2,
26=(22)3=43,
∵26=a2=4b,
∴a=±8,b=3,
∴a+b=11或-5.
解答题
12.(1)若33·9m+4÷272m-1的值为729,试求m的值;
解:∵33·9m+4÷272m-1
=33·32(m+4)÷33(2m-1)
=33+2(m+4)-3(2m-1)
=314-4m
=729
=36,
∴14-4m=6,
解得m=2.
(2)已知3m=4,3m-4n=,求200n的值;
解:∵3m=4,
∴3m-4n=3m÷34n=4÷34n=,
∴34n=81=34,
∴4n=4,即n=1,
∴200n=200.
(3)若mp=,m2q=7,mr=-,求m3p+4q-2r的值.
解:∵mp=,m2q=7,mr=-,
∴m3p+4q-2r
=(mp)3×(m2q)2÷(mr)2
=()3×72÷(-)2
=×72×
=.
谢 谢 观 看
第8课时 整式的乘法(5)
第十四章 整式的乘法与因式分解
一、选择题
1.计算(-4x3+2x)÷2x的结果正确的是( A )
A.-2x2+1 B.2x2+1
C.-2x3+1 D.-8x4+2x
2.2x3可以表示为( C )
A.x3·x3 B.2x4-x
C.x3+x3 D.2x6÷x2
A
C
4.面积为9a2-6ab+3a的长方形一边长为3a,另一边长为( D )
A.2a-3 B.2a-3b+1
C.3a-2b D.3a-2b+1
D
3.已知8a3bm÷28an+1b2=b2,则m,n的值分别为( B )
A.4,3 B.4,2 C.2,2 D.2,3
B
二、填空题
5.若8a5bn÷2amb=4a2b5,则mn= 18 .
6.已知长方形的面积为6a2b-4a2+2a,宽为2a,则长方形的周长为 6ab+2 .
18
6ab+2
三、解答题
7.计算:
(1)8x8÷2x3;
解:原式=4x5.
(2)20x3y5z÷(-5x2y3);
解:原式=-4xy2z.
(3)(-4a5b3)2÷8a2b3;
解:原式=16a10b6÷8a2b3
=2a8b3.
(4)9a5b4÷3a2b4-a·(-5a2);
解:原式=3a3+5a3
=8a3.
(5)-2x6-·8x5+(2x4)3÷(-x)5;
解:原式=-2x6-x2·8x5+8x12÷(-x5)
=-2x6-2x7-8x7
=-2x6-10x7.
(6)3a2b2÷a2+b·(a2b-3ab)-(2b)2.
解:原式=3b2+a2b2-3ab2-4b2
=-b2+a2b2-3ab2.
8.计算:
(1)(4m3-3m2n+2m)÷2m;
解:原式=2m2-mn+1.
(2)÷;
解:原式=-6x+2y-1.
(3)[6(m+n)a+3z4-6(m+n)a-2z2+3(m+n)a-1z]÷3(m+n)a-2z;
解:原式=2(m+n)5z3-2z+m+n.
(4)(3x4-2x3)÷(-x)-(x-x2)·3x.
解:原式=-3x3+2x2-(3x2-3x3)
=-3x3+2x2-3x2+3x3
=-x2.
一、选择题
9.已知x3+(a-1)x-6能被x-2整除,则a的值为( C )
A.1 B.-1 C.0 D.2
C
二、填空题
10.若-5a2m-3bn+4÷3am+2b5=-a4b2,则m÷n= 3 .
3
三、解答题
11.先化简,再求值:[(2x+y)(2x-y)-3(2x2-xy)+y2]÷,其中x=2,y=-1.
解:原式=(4x2-y2-6x2+3xy+y2)÷
=(-2x2+3xy)÷
=4x-6y,
当x=2,y=-1时,
原式=8+6=14.
12.阅读材料:
∵(x-2)(x+3)=x2+x-6,
∴(x2+x-6)÷(x-2)=x+3,
即x2+x-6能被x-2整除,
∴x-2是x2+x-6的一个因式,且当x=2时,x2+x-6=0.
解答问题:
(1)由(x+2)(x+3)=x2+5x+6,得x2+5x+6能被 整除,且当x= 时,x2+5x+6=0;
解:(1)∵(x+2)(x+3)=x2+5x+6,
∴x2+5x+6能被x+2整除或者能被x+3整除,
当x=-2或-3时,x2+5x+6=0,
故答案为:x+2或x+3,-2或-3;
x+2或x+3
-2或-3
(2)根据材料,已知多项式x2+mx-14能被x+2整除,试求m的值.
解:(2)∵x2+mx-14能被x+2整除,
当x=-2时,
原式=(-2)2+m×(-2)-14=0,
解得m=-5.
解答题
13.(1)计算:(a6b2)n+1÷(-anb)3÷a2n-3bn;
解:原式=a6n+6b2n+2÷(-a3nb3)÷a2n-3bn
=-a3n+6b2n-1÷a2n-3bn
=-an+9bn-1.
(2)已知(xmyn)2÷(x2y)3=x4y5,求2m-n的值;
解:∵(xmyn)2÷(x2y)3=x2m-6y2n-3=x4y5,
∴2m-6=4,2n-3=5,
解得:m=5,n=4,
则2m-n=2.
(3)计算:÷[3(-x-y)2(x-y)2]2.
解:原式=36(x+y)6(x-y)4÷[9(x+y)4(x-y)4]
=4(x+y)2
=4x2+8xy+4y2.
谢 谢 观 看
第9课时 专题幂的运算
第十四章 整式的乘法与因式分解
解答题
1.计算:
(1)×;
解:原式=
=.
(2)xm+15·xm-1;
解:原式=x(m+15)+(m-1)
=x2m+14.
(3)(-x)·(-x)6;
解:原式=(-x)7
=-x7.
(4)-m3·m4;
解:原式=-m3+4
=-m7.
(5)(3ab7)2;
解:原式=9a2b14.
(6)(-m)8÷(-m)3;
解:原式=(-m)5
=-m5.
(7)(xy)7÷(xy)4;
解:原式=(xy)3
=x3y3.
(8)x2m+2÷xm+2;
解:原式=x2m+2-m-2
=xm.
解:原式=(2a+b)(2n+1)+3+(n-4)
=(2a+b)3n.
(11)(x-y)2·(y-x)5.
解:原式=(y-x)2·(y-x)5
=(y-x)7.
(9)(x-y)5÷(y-x)3;
解:原式=-(y-x)5÷(y-x)3
=-(y-x)2.
(10)(2a+b)2n+1·(2a+b)3·(2a+b)n-4;
2.计算:
(1)x4·(-x)5+(-x)4·x5;
解:原式=-x9+x9
=0.
(2)(m4)2+m5·m3+(-m)4·m4;
解:原式=m4×2+m5+3+m4+4
=3m8.
(3)(-3a2)3+(-4a3)2;
解:原式=-27a6+16a6
=-11a6.
(4)x·(x2)2+x7÷x2-4x3·x2;
解:原式=x5+x5-4x5
=-2x5.
(5)(-3a4)2-a·a3·a4-a10÷a2;
解:原式=9a8-a8-a8
=7a8.
(6)0.254×44-×;
解:原式=(0.25×4)4-×
=1-×
=1-1×
=.
(5)(-3a4)2-a·a3·a4-a10÷a2;
解:原式=9a8-a8-a8
=7a8.
(7)×24+(-2)0-(-0.1)2024×102024;
解:原式=×2+1-(-0.1×10)2024
=-2+1-1
=-2.
(8)(a-b)2·(b-a)3+(a-b)4·(b-a).
解:原式=(b-a)5+(b-a)5
=2(b-a)5.
3.(1)已知xa+b=6,xb=3,求xa的值;
解:xa=xa+b-b=xa+b÷xb=6÷3=2.
(2)已知xm=5,xn=7,求x2m+n的值;
解:∵xm=5,xn=7,
∴x2m+n=xm·xm·xn=5×5×7=175.
(3)已知2x+3y-2=0,求9x·27y的值;
解:∵2x+3y-2=0,∴2x+3y=2,
∴9x·27y=32x·33y=32x+3y=32=9.
(4)已知10m=20,10n=4,求2m-n的值;
解:∵102m-n==100=102,
∴2m-n=2.
(5)若32·92a+1÷27a+1=81,求a的值;
解:∵32·92a+1÷27a+1=81,
∴32·32(2a+1)÷33(a+1)=34,
即2+2(2a+1)-3(a+1)=4,
解得a=3.
(6)若33x+1·53x+1=152x+4,求x的值.
解:33x+1·53x+1=153x+1=152x+4,
∴3x+1=2x+4,
∴x=3.
4.比较312×510与310×512的大小.
解:312×510=(3×5)10×32,
310×512=(3×5)10×52,
∵32<52,
∴312×510<310×512.
谢 谢 观 看
第10课时 专题整式的乘除
第十四章 整式的乘法与因式分解
解答题
1.计算:
(1)(-12a2b)÷2ab;
解:原式=-6a.
(2)(-2xy2)2·3x2y;
解:原式=4x2y4·3x2y
=12x4y5.
(3)5(a4)3+(-2a3)2·(-a6);
解:原式=5a12-4a6·a6
=a12.
(4)2x3y·(-2xy)+÷2x2.
解:原式=-4x4y2-8x9y3÷2x2
=-4x4y2-4x7y3.
2.计算:
(1)·ab;
解:原式=a2b3-a2b2.
(2)(-2a2)(3ab2-5ab3);
解:原式=-6a3b2+10a3b3.
(3)-3x·;
解:原式=-x3y3-6xy2+3x.
(4)·5xy2÷(-10x6y5)+(x2y-2xy)÷xy.
解:原式=8x6y3·5xy2÷(-10x6y5)+x-2
=40x7y5÷(-10x6y5)+x-2
=-4x+x-2
=-3x-2.
3.计算:
(1)(x-2)(x+3);
解:原式=x2+3x-2x-6
=x2+x-6.
(2)(3x+9)(6x-8);
解:原式=18x2-24x+54x-72
=18x2+30x-72.
(3)(a+b+1)(2a-b);
解:原式=2a2-ab+2ab-b2+2a-b
=2a2+ab+2a-b2-b.
(4)(2a-7)(a+6)-(a-2)(2a+1);
解:原式=2a2+12a-7a-42-(2a2+a-4a-2)
=2a2+5a-42-2a2+3a+2
=8a-40.
(5)(x-2)(x+1)-2(x-3)(x+2).
解:原式=x2+x-2x-2-2x2-4x+6x+12
=-x2+x+10.
4.(1)计算:(-3a2b3)÷;
解:原式=(-3a2b3)÷(3ab-ab2-2ab+ab2)
=(-3a2b3)÷ab
=-3ab2.
(2)先化简,再求值:3a(2a2-4a+3)-2a2(3a+4),其中a=-2.
解:原式=6a3-12a2+9a-6a3-8a2
=-20a2+9a,
当a=-2时,
原式=-20×4-9×2=-98.
5.将多项式(x-2)(x2+ax-b)展开后不含x2和x的项,试求2a2-b的值.
解:原式=x3+ax2-bx-2x2-2ax+2b
=x3+(a-2)x2-(2a+b)x+2b,
∵多项式不含x2和x的项,
∴a-2=0,-(2a+b)=0,
∴a=2,b=-4,
∴2a2-b=2×22+4=12.
6.解不等式组:
.
解:不等式组可化为:
,
解不等式①得:x<,
解不等式②得:x<-1,
∴不等式组的解集为x<-1.
7.长方形的长为a厘米,宽为b厘米,其中a>b,如果将原长方形的长和宽各增加3厘米,得到的新长方形的面积为S1平方厘米,如果将原长方形的长和宽分别减少2厘米,得到的新长方形的面积为S2平方厘米.
(1)若a、b为正整数,请说明:S1与S2的差一定是5的倍数;
解:(1)由题意得:
S1=(a+3)(b+3)=ab+3(a+b)+9,
S2=(a-2)(b-2)=ab-2(a+b)+4,
∴S1-S2=ab+3(a+b)+9-ab+2(a+b)-4
=5(a+b)+5=5(a+b+1),
∴S1与S2的差一定是5的倍数;
(2)如果S1=2S2,求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积;
解:(2)∵S1=2S2,
∴ab+3a+3b+9=2(ab-2a-2b+4),
∴ab-7a-7b-1=0,
∴ab-7a-7b=1,
∵新长方形的面积为(a-7)(b-7)=ab-7a-7b+49=1+49=50平方厘米,
∴将原长方形的长和宽分别减少7厘米后得到的新长方形的面积为50平方厘米;
(3)如果用一个面积为S1的长方形和两个面积为S2的长方形恰好能没有缝隙没有重叠地拼成一个正方形,求a,b的值.
解:(3)由题意可得方程组:,
或,
解得或(不符合题意,舍),
∴a的值为7,b的值为4.5.
谢 谢 观 看
第11课时 平方差公式
第十四章 整式的乘法与因式分解
一、选择题
1.下列式子中可以用平方差公式计算的是( D )
A.(x+2)(x+2) B.(x+2)(-x-2)
C.(x-2)2 D.(x+2)(x-2)
2.下列计算正确的是( C )
A.x3+4x3=5x6
B.a2·a3=a6
C.(-2x3)4=16x12
D.(x+2y)(x-2y)=x2-2y2
D
C
3.若a-b=3,a2-b2=-9,则a+b=( D )
A.2 B.3 C.-2 D.-3
4.如图,边长为a的正方形中剪去一个边长为b的小正方形,剩下部分正好拼成一个等腰梯形,利用这两幅图形阴影部分的面积,能验证的数学公式是( A )
A.a2-b2=(a+b)(a-b)
B.(a+b)2-(a-b)2=4ab
C.(a+b)2=a2+2ab+b2
D.(a-b)2=a2-2ab+b2
第4题图
D
A
二、填空题
5.计算:2024×2022-20232= -1 .
6.若a2-4b2=12,且a-2b=-3,则a+b= -3.75 .
-1
-3.75
三、解答题
7.计算:
(1)(a+5)(a-5);
解:原式=a2-25.
(2)(x-2y)(2y+x);
解:原式=x2-4y2.
(3)(3m-2n)(-3m-2n);
解:原式=-(3m-2n)(3m+2n)
=-(9m2-4n2)
=4n2-9m2.
(4)(5ab-3xy)(-3xy-5ab);
解:原式=-(5ab-3xy)(5ab+3xy)
=-(25a2b2-9x2y2)
=9x2y2-25a2b2.
(5)(x3+2)(x3-2).
解:原式=(x3)2-22
=x6-4.
8.计算:
(1)20232-2022×2024;
解:原式=20232-(2023-1)(2023+1)
=20232-20232+12
=1.
(2)(5m+2)(5m-2)-(3m+1)(2m-1).
解:原式=(25m2-4)-(6m2-3m+2m-1)
=25m2-4-6m2+m+1
=19m2+m-3.
9.(1)已知m2-n2=24,m+n=8,求m-n的值;
解:∵m2-n2=(m+n)(m-n)=24,m+n=8,
∴m-n=3.
(2)先化简,再求值:(x+2y)(x-2y)-(2x-y)(-2x-y),其中x=8,y=-8.
解:原式=x2-4y2-y2+4x2
=5x2-5y2,
∵x=8,y=-8,
∴原式=5×82-5×(-8)2=0.
一、填空题
10.计算:(5+1)(52+1)(54+1)(58+1)(516+1)+= .
11.已知a1=(1+)(1-),a2=(1+)(1-),a3=(1+)(1-),…,an=(1+)(1-),Sn=a1·a2·a3·…·an,则2S2023= .
二、解答题
12.计算下列各题:
(1)1002-992+982-972+962-952+…+22-12;
解:原式=(100+99)(100-99)+(98+97)(98-97)+(96+95)(96-95)
+…+(2+1)(2-1)
=100+99+98+97+…+2+1
=5050.
(2)++…+.
解:原式=++…+
=-1×
=-50.
解答题
13.(1)计算并观察下列各式:
第1个:(a-b)(a+b)= ;
第2个:(a-b)(a2+ab+b2)= ;
第3个:(a-b)(a3+a2b+ab2+b3)= ;
……,
这些等式反映出多项式乘法的某种运算规律;
解:(1)a2-b2;a3-b3;a4-b4;
(2)猜想:若n为大于1的正整数,则(a-b)(an-1+an-2b+an-3b2+…+a2bn-3+abn-2+bn-1)= ;
an-bn
(3)利用(2)的猜想计算:2n-1+2n-2+2n-3+…+23+22+1= ;
2n-3
(4)拓展与应用:计算3n-1+3n-2+3n-3+…+33+32+1的值.
解:原式=×(3-1)(3n-1+3n-2+3n-3+…+33+32+3+1)-3
=×(3n-1n)-3
=.
谢 谢 观 看
第12课时 完全平方公式(1)
第十四章 整式的乘法与因式分解
一、选择题
1.(1)计算:(c-a)2=( D )
A.c2-a2 B.a2+2ac+c2
C.c2+a2 D.c2-2ac+a2
(2)计算:(-a-b)2=( B )
A.a2+b2 B.a2+2ab+b2
C.a2-b2 D.a2-2ab+b2
D
B
(4)若(7x-a)2=49x2-bx+9,则|a+b|的值为( D )
A.18 B.24 C.39 D.45
D
(3)计算(x+2)2的结果为x2+□x+4,则“□”中的数为( D )
A.-2 B.2 C.-4 D.4
D
2.下列各式能写成两数和的平方的是( D )
A.x2+2x-1 B.1+x2
C.x2+x+1 D.x2+4x+4
3.如图,将图1中阴影部分拼成图2,根据两个图形中阴影部分的关系,下列计算公式可以表示该关系的是( B )
A.(a+b)(a-b)=a2-b2
B.(a-b)2=a2-2ab+b2
C.(a+b)2=a2+2ab+b2
D.(a+b)2=(a-b)2+4ab
第3题图
D
B
二、填空题
4.填上适当的数或代数式,使等式成立:
(1)x2+10x+ 25 =(x+ 5 )2;
(2)m2-8m+ 16 =(m- 4 )2;
(3)x2+xy+ y2 =(x+ y )2.
25
5
16
4
y2
y
三、解答题
5.计算:
(1)(2a+3b)2;
解:原式=(2a)2+2·2a·3b+(3b)2
=4a2+12ab+9b2.
(2)(-2m+n)2;
解:原式=(-2m)2-2·2m·n+n2
=4m2-4mn+n2.
(3)(-2m-n)2.
解:原式=(-2m)2+2(-2m)(-n)+(-n)2
=4m2+4mn+n2.
6.计算:
(1)(2a+b)2-(2a-b)2;
解:原式=4a2+4ab+b2-(4a2-4ab+b2)
=8ab.
(2)(3x-5)2-(2x+7)2.
解:原式=9x2-30x+25-(4x2+28x+49)
=9x2-30x+25-4x2-28x-49
=5x2-58x-24.
7.解方程:-=1.
解:去括号得:x2+x+-x2+=1,
解得:x=.
8.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆形钢板,求剩下的钢板的面积.
第8题图
解:剩下的钢板的面积为π-π-=πab.
一、选择题
9.若n为正整数,则(2n+1)2-(2n-1)2( B )
A.一定能被6整除
B.一定能被8整除
C.一定能被10整除
D.一定能被12整除
B
二、填空题
10.(1)若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k= -3 ;
(2)若x2-2(k-1)x+9是完全平方式,则k的值为 4或-2 .
-3
4或-2
三、解答题
11.计算:
(1)(2x-1)(4x2-1)(2x+1);
解:原式=(4x2-1)(4x2-1)
=(4x2-1)2
=16x4-8x2+1.
(2)(x+y)2-4(x+y)(x-y)+4(x-y)2;
解:原式=[x+y-2(x-y)]2
=(3y-x)2
=x2-6xy+9y2.
(3)4(a+2)2-7(a+3)(a-3)+3(a-1)2.
解:原式=4(a2+4a+4)-7(a2-9)+3(a2-2a+1)
=4a2+16a+16-7a2+63+3a2-6a+3
=10a+82.
解答题
12.如图,大正方形、小正方形的边长分别为a、b.
(1)用含a、b的代数式表示阴影部分的面积S;
解:(1)∵大正方形、小正方形的边长分别为a、b,
∴S=a2+b2-a2-(a+b)b
=a2+b2-ab;
第12题图
(2)如果a+b=9,ab=6,求阴影部分的面积.
解:(2)∵a+b=9,ab=6,
∴S=a2+b2-ab
=(a+b)2-ab
=×92-×6
=,
故阴影部分的面积为.
第12题图
谢 谢 观 看
第13课时 完全平方公式(2)
第十四章 整式的乘法与因式分解
一、选择题
1.计算(x-2)2正确的是( D )
A.x2-4 B.x2-4x-4
C.x2-2x+4 D.x2-4x+4
2.将10.52变形正确的是( C )
A.10.52=102+0.52
B.10.52=(11+0.5)(11-0.5)
C.10.52=102+2×10×0.5+0.52
D.10.52=112-11×0.5+0.52
D
C
3.若x2+(a-1)x+25是一个完全平方式,则a的值为( B )
A.-9 B.-9或11
C.9或-11 D.11
4.若ab=1,a+b=3,则2a2+2b2的值是( D )
A.7 B.10 C.12 D.14
B
D
二、填空题
5.(1)若a2+b2=19,a+b=5,则ab= 3 ;
(2)若a2+b2=13,(a-b)2=1,则(a+b)2= 25 .
3
25
三、解答题
6.计算:
(1)9992;
解:原式=(1000-1)2
=1000000-2000+1
=998001.
(2)1.23452+0.76552+2.469×0.7655.
解:原式=1.23452+2×1.2345×0.7655+0.76552
=(1.2345+0.7655)2
=4.
7.计算:
(1);
解:原式=
=
=1-x2+x4.
(2)(3x+2y-4)(2y-3x+4);
解:原式=[2y+(3x-4)][2y-(3x-4)]
=(2y)2-(3x-4)2
=4y2-9x2+24x-16.
(3)(m-n-3)2.
解:原式=(m-n)2+2(m-n)×(-3)+9
=m2+n2-2mn+6n-6m+9.
8.(1)已知xy=1,x-y=5,求x2+y2的值;
解:将x-y=5两边同时平方,
得:(x-y)2=25,
即x2+y2-2xy=25,
∵xy=1,
∴x2+y2=25+2xy=27.
(2)已知a-=4,求a2+的值.
解:将a-=4两边同时平方,
得:=42=16,
即a2+-2=16,
∴a2+=16+2=18.
一、填空题
9.多项式1+4a2加上一个单项式后,使它成为一个整式的完全平方式,则单项式可以为 4a4(或±4a或-1或-4a2) .(写出一个即可)
10.已知(a-2022)2+(2023-a)2=5,则(a-2022)(a-2023)= 2 .
11.如果a+b+|-1|=4+2-4,那么a+2b-3c= 0 .
4a4(或±4a或-1或-4a2)
2
0
二、解答题
12.比较代数式2x2+5x-1与代数式x2+7x-4的值的大小.
解:(2x2+5x-1)-(x2+7x-4)
=2x2+5x-1-x2-7x+4
=x2-2x+3
=(x-1)2+2,
∵(x-1)2+2>0,
∴代数式2x2+5x-1的值比代数式x2+7x-4的值大.
解答题
13.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例,如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应(a+b)3=a3+3a2b+3ab2+b3展开式中的系数.
根据上述规律,解答下列问题:
(1)求(a+b)5的展开式;
解:(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
第13题图
(2)计算:25+5×24+10×23+10×22+5×2+1;
解:(2)25+5×24+10×23+10×22+5×2+1
=25+5×24×1+10×23×12+10×22×13+5×2×14+15
=(2+1)5
=35;
第13题图
(3)若(x+1)5·(2x2+ax-b)(a、b为常数)的展开式中不含x2和x的项,求a、b的值.
解:(3)(x+1)5=x5+5x4+10x3+10x2+5x+1,
∵展开式中不含x2和x的项,
∴取(10x2+5x+1)(2x2+ax-b)
=20x4+10ax3-10bx2+10x3+5ax2-5bx+2x2+ax-b
=20x4+(10a+10)x3+(-10b+5a+2)x2+(-5b+a)x-b,
∴含x2的项的系数为-10b+5a+2=0,
含x的项的系数为-5b+a=0,
∴a=-,b=-.
谢 谢 观 看
第14课时 专题乘法公式
第十四章 整式的乘法与因式分解
解答题
1.计算:
(1)(x-3)(x+3);
解:原式=x2-9.
(2)(x+3y)(x-3y);
解:原式=x2-9y2.
(3);
解:原式=-22
=x6-4.
(4)(2m-n)(-2m-n);
解:原式=(n-2m)(n+2m)
=n2-4m2.
(5)101×99;
解:原式=(100+1)(100-1)
=1002-1
=9999.
(6)145.52-135.52.
解:原式=(145.5+135.5)(145.5-135.5)
=281×10
=2810.
2.计算:
(1)(4m+n)2; (2);
解:原式=16m2+8mn+n2;
解:原式=y2-y+.
(3)(-2x+5)2; (4);
解:原式=4x2-20x+25;
解:原式=x2-xy+y2.
(5)1022; (6)992.
解:原式=(100+2)2
=10000+400+4
=10404;
解:原式=(100-1)2
=10000-200+1
=9801.
3.计算:
(1)(x+2y)2(x-2y)2;
解:原式=[(x+2y)(x-2y)]2
=(x2-4y2)2
=x4-8x2y2+16y4.
(2)(1-3y)(1+3y)(1+9y2);
解:原式=(1-9y2)(1+9y2)
=1-81y4.
(3)1232-122×124;
解:原式=1232-(123-1)(123+1)
=1232-(1232-1)
=1.
(4)(3-2x+y)(3+2x-y).
解:原式=[3-(2x-y)][3+(2x-y)]
=9-(2x-y)2
=9-4x2+4xy-y2.
4.(1)计算:[(a-2b)(a+2b)-(2b-a)2]÷(-4b);
解:原式=(a2-4b2-4b2+4ab-a2)÷(-4b)
=(-8b2+4ab)÷(-4b)
=2b-a.
(2)先化简,再求值:(2x+3y)(2x-3y)-4x(x-y)+(x-2y)2,其中x,y满足x2-6x+9+|2y-1|=0;
解:原式=4x2-9y2-4x2+4xy+x2-4xy+4y2
=x2-5y2,
由题意得(x-3)2+|2y-1|=0,
∴x-3=0,2y-1=0,解得x=3,y=,
∴原式=9-=.
(3)已知x2+y2-2x+6y+10=0,求x+y的值;
解:原方程变形为:x2-2x+1+y2+6y+9=0,
即(x-1)2+(y+3)2=0,
∴x-1=0,y+3=0,
∴x=1,y=-3,
∴x+y=-2.
解:①原式=(x+y)2-2xy,
当x+y=5,xy=-3时,
原式=25-2×(-3)
=31;
②原式=1-y-x+xy
=1-(x+y)+xy,
当x+y=5,xy=-3时,
原式=1-5+(-3)
=-7.
(4)已知x+y=5,xy=-3,求:
①x2+y2的值;
②(1-x)(1-y)的值.
5.计算:(1-)(1-)…(1-)(1-).
解:原式=(1-)(1+)(1-)(1+)×…×(1-)(1+)(1-)
(1+)
=××××…××××
=×
=.
6.阅读理解:
若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值.
解:设80-x=a,x-60=b,
则ab=(80-x)(x-60)=30,
a+b=80-x+x-60=20,
∴(80-x)2+(x-60)2=a2+b2=(a+b)2-2ab=202-2×30=340.
解决问题:
若x满足(30-x)(x-20)=-10,求(30-x)2+(x-20)2的值.
解:设30-x=a,x-20=b,
则ab=(30-x)(x-20)=-10,
a+b=30-x+x-20=10,
∴(30-x)2+(x-20)2
=a2+b2
=(a+b)2-2ab
=102-2×(-10)
=120.
谢 谢 观 看
第15课时 提公因式法
第十四章 整式的乘法与因式分解
一、选择题
1.下列从左到右的变形是分解因式的是( C )
A.3x+3y-5=3(x+y)-5
B.(x+1)(x-1)=x2-1
C.x2-9=(x+3)(x-3)
D.x2+1=x
2.多项式4xy3z-8x3y2的公因式是( D )
A.4xy B.-4xyz C.-4x2y D.4xy2
C
D
3.将x2+mx+n分解成(x-7)(x+2),则m,n的值分别为( D )
A.5,-14 B.-5,14
C.5,14 D.-5,-14
D
二、填空题
4.分解因式:3a2b+6ab+3b= 3b(a+1)2 .
5.若ab=-3,a-2b=5,则a2b-2ab2的值是 -15 .
3b(a+1)2
-15
三、解答题
6.分解因式:
(1)3x2y-6xy;
解:原式=3xy(x-2).
(2)5x2y3-25x3y2;
解:原式=5x2y2(y-5x).
(3)15x3y2+5x2y-20x2y3;
解:原式=5x2y(3xy+1-4y2).
(4)-4m3+16m2-26m;
解:原式=-2m(2m2-8m+13).
(5)-9x3y2-6x2y2+3xy;
解:原式=-3xy(3x2y+2xy-1).
(6)2m(a-b)-3n(a-b);
解:原式=(a-b)(2m-3n).
(7)8amb3-12am+1b2+16am+2b.
解:原式=4amb(2b2-3ab+4a2).
7.计算:123×6.28+628×1.32-15.5×62.8.
解:原式=6.28×(123+100×1.32-15.5×10)
=6.28×(123+132-155)
=628.
8.利用提公因式法先化简,再求值:(a-b)2+b(a-b),其中a=2,b=-.
解:原式=(a-b)[(a-b)+b]
=a(a-b)
=a2-ab,
当a=2,b=-时,
原式=22-2×=5.
解答题
9.分解因式:
(1)4a2n+1bm-6an+2bm-1(m、n为大于1的自然数);
解:原式=2an+2bm-1(2an-1b-3).
(2)3a(a+b)(a-b)-2b(b-a);
解:原式=3a(a+b)(a-b)+2b(a-b)
=(a-b)(3a2+3ab+2b).
(3)5a3b(a-b)3-10a4b3(b-a)2.
解:原式=5a3b(a-b)2(a-b-2ab2).
10.已知正整数n满足5n+2×2n+1-5n+1×2n+2=3000,求n的值.
解:∵5n+2×2n+1-5n+1×2n+2
=5×10n+1-2×10n+1
=3×10n+1,
∴3×10n+1=3000,
即10n+1=1000=103,
∴n=2.
11.计算:
(1);
解:原式=
=
=-23
=-8.
(2).
解:原式=
=.
解答题
12.阅读材料:
若一个整式A等于整式B与整式C之积,则称整式B和整式C为整式A的因式.
如:①∵36=4×9,∴4和9是36的因数;
∵x2-x-2=(x+1)(x-2),
∴x+1和x-2是x2-x-2的因式;
②若x+1是x2+ax-2的因式,求常数a的值.
解:∵x+1是x2+ax-2的因式,
∴存在一个整式mx+n,使得x2+ax-2=(x+1)(mx+n),
∵当x=-1时,(x+1)(mx+n)=0,
∴当x=-1时,x2+ax-2=0,
∴1-a-2=0,解得a=-1.
根据材料内容,解答下列问题:
(1)若x+5是整式x2+mx-10的一个因式,则m= ;
解:(1)∵x+5是整式x2+mx-10的一个因式,
∴当x=-5时,x2+mx-10=0,
即25-5m-10=0,
解得m=3.
3
(2)若整式x2-1是3x4-ax2+bx+1的因式,求的值.
解:(2)∵整式x2-1是3x4-ax2+bx+1的因式,
∴存在一个整式3x2+mx-1,使得3x4-ax2+bx+1=(x2-1)(3x2+mx-1),
∴当x=1时,(x2-1)(3x2+mx-1)=0,
即3x4-ax2+bx+1=0,
则3-a+b+1=0①,
当x=-1时,(x2-1)(3x2+mx-1)=0,
即3x4-ax2+bx+1=0,
则3-a-b+1=0②,
联立①②,解得a=4,b=0,
∴==2.
谢 谢 观 看
第16课时 公式法(1)
第十四章 整式的乘法与因式分解
一、选择题
1.下列多项式中,能用公式法分解因式的是( C )
A.x2-xy B.x2+xy C.x2-y2 D.x2+y2
2.因式分解x2y-4y的正确结果是( A )
A.y(x+2)(x-2) B.y(x+4)(x-4)
C.y(x2-4) D.y(x-2)2
3.已知a-b=1,则a2-b2-2b的值为( C )
A.4 B.3 C.1 D.0
C
A
C
二、填空题
4.分解因式:
(1)16x2-25= (4x+5)(4x-5) ;
(2)4a3b3-ab= ab(2ab+1)(2ab-1) ;
(3)-x2+2= -(x+2)(x-2) ;
(4)m2(x-2)+(2-x)= (x-2)(m+1)(m-1) .
5.计算:20232-20222= 4045 .
6.若|x+y-5|+(x-y+1)2=0,则x2-y2= -5 .
(4x+5)(4x-5)
ab(2ab+1)(2ab-1)
-(x+2)(x-2)
(x-2)(m+1)(m-1)
4045
-5
三、解答题
7.用平方差公式分解因式:
(1)36-x2;
解:原式=(6+x)(6-x).
(2)-a2+b2;
解:原式=(b+a)(b-a).
(3)x2-16y2;
解:原式=(x+4y)(x-4y).
(4)x2y2-z2;
解:原式=(xy+z)(xy-z).
(5)(x+2)2-9;
解:原式=(x+2+3)(x+2-3)
=(x+5)(x-1).
(6)a4-16;
解:原式=(a2+4)(a2-4)
=(a2+4)(a+2)(a-2).
(7)x2(x-2)+4y2(2-x).
解:原式=(x-2)(x2-4y2)
=(x-2)(x+2y)(x-2y).
8.已知x、y满足,求x2-y2的值.
解:,
①+②,得3x+3y=15,即x+y=5,
①-②,得x-y=3,
∴x2-y2=(x+y)(x-y)=15.
9.若n为整数,证明:(n+13)2-n2能被13整除.
证明:∵(n+13)2-n2
=(n+13-n)(n+13+n)
=13(2n+13),
∵n为整数,
∴(n+13)2-n2能被13整除.
一、填空题
10.如果(a2+b2+2)(a2+b2-2)=5,那么a2+b2= 3 .
11.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:x-y=0,x+y=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3-xy2,取x=13,y=3时,用上述方法产生的密码是: 131610(答案不唯一) .(写出一个即可)
3
131610
(答案不唯一)
二、解答题
12.把下列各式分解因式:
(1)(2x+3y)2-(3x+2y)2;
解:原式=(2x+3y+3x+2y)(2x+3y-3x-2y)
=(5x+5y)(-x+y)
=-5(x+y)(x-y).
(2)9(a+b)2-64(a-b)2.
解:原式=(3a+3b-8a+8b)(3a+3b+8a-8b)
=(11b-5a)(11a-5b).
13.(1)填空:a2-b2=(a-b)( );
a3-b3=(a-b)(a2+ab+b2);
a4-b4=(a-b)(a3+a2b+ab2+b3);
a5-b5=(a-b)( );
解:(1)a2-b2=(a-b)(a+b);
a3-b3=(a-b)(a2+ab+b2);
a4-b4=(a-b)(a3+a2b+ab2+b3);
a5-b5=(a-b)(a4+a3b+a2b2+ab3+b4),
(2)猜想:an-bn=(a-b)( );
(其中n为正整数,且n≥2)
an-1+an-2b+…+abn-2+bn-1
a+b
a4+a3b+a2b2+ab3+b4
(3)利用(2)猜想的结论化简:29+28+27+…+23+22+2.
解:(3)29+28+27+…+23+22+2
=(2-1)(29+28·1+27·12+…+23·16+22·17+2·18+19)-1
=210-1-1
=1024-2
=1022.
解答题
14.计算:
(1)++…+;
解:原式=++…+
=1-2+2-3+…+99-100
=1-100
=-99.
(2)(1-)(1-)(1-)…(1-)(1-).
解:原式=(1-)(1+)(1-)(1+)…(1-)(1+)(1-)
(1+)
=××××…××××
=×
=.
谢 谢 观 看
第17课时 公式法(2)
第十四章 整式的乘法与因式分解
一、选择题
1.下列各式中能用完全平方公式进行因式分解的是( D )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
2.分解因式:4x2+4x+1=( C )
A.4x(x+1)+1 B.(4x+1)2
C.(2x+1)2 D.(2x-1)2
D
C
3.分解因式(x-1)2-2(x-1)+1的结果是( D )
A.(x-1)(x-2) B.x2
C.(x+1)2 D.(x-2)2
D
二、填空题
4.分解因式:
(1)2a3-8a2+8a= 2a(a-2)2 ;
(2)3x2-6x+3= 3(x-1)2 ;
(3)3m2-6mn+3n2= 3(m-n)2 .
2a(a-2)2
3(x-1)2
3(m-n)2
三、解答题
5.分解因式:
(1)-x2+4xy-4y2;
解:原式=-(x2-4xy+4y2)
=-(x-2y)2.
(2)a2x-6ax+9x;
解:原式=x(a2-6a+9)
=x(a-3)2.
(3)-a2+ab-b2;
解:原式=-(a-b)2.
(4)(x-y)2+4xy;
解:原式=(x+y)2.
(5)-4a2;
解:原式=(a2+1+2a)(a2+1-2a)
=(a+1)2(a-1)2.
(6)(2x+y)2-2(2x+y)(x-2y)+(x-2y)2.
解:原式=[2x+y-(x-2y)]2
=(x+3y)2.
6.计算:40×3.152+80×3.15×1.85+40×1.852.
解:原式=40×(3.152+2×3.15×1.85+1.852)
=40×(3.15+1.85)2
=40×25
=1000.
7.阅读材料:
例:求代数式y2+4y+8的最小值.
解:∵y2+4y+8=(y2+4y+4)+4=(y+2)2+4≥4,
∴当y=-2时,代数式y2+4y+8有最小值,最小值是4.
仿照例题,解决下列问题:
(1)求代数式m2+2m+3的最小值;
解:(1)m2+2m+3
=(m2+2m+1)+2
=(m+1)2+2≥2,
∴当m=-1时,代数式m2+2m+3有最小值,最小值是2;
(2)求代数式-m2+3m+的最大值.
解:(2)-m2+3m+
=-++
=-+3≤3,
∴当m=时,代数式-m2+3m+有最大值,最大值是3.
一、填空题
8.(1)设a、b为整数,且a2-2a+b2+6b=-10,则(b+1)a的值为 -2 ;
(2)已知实数x满足x+=3,则的值为 ;
(3)若x=+1,则(x+1)2-4(x+1)+4的值为 2 .
-2
2
二、解答题
9.分解因式:
(1)a2-b2-2a+2b;
解:原式=(a+b)(a-b)-2(a-b)
=(a-b)(a+b-2).
(2)m2-25+9n2+6mn;
解:原式=(m2+6mn+9n2)-25
=(m+3n)2-25
=(m+3n+5)(m+3n-5).
(3)(a+c)(a-c)+b(b+2a).
解:原式=a2-c2+b2+2ab
=a2+2ab+b2-c2
=(a+b)2-c2
=(a+b+c)(a+b-c).
10.若x+y=2,y-z=-1,求代数式x2+y2+z2+xy-yz+xz的值.
解:∵x+y=2,y-z=-1,
∴x+z=3,
x2+y2+z2+xy-yz+xz
=(2x2+2y2+2z2+2xy-2yz+2xz)
=[(x+y)2+(y-z)2+(x+z)2]
=[22+(-1)2+32]
=7.
解答题
11.阅读材料:
例:若x满足(210-x)(x-200)=-204,试求(210-x)2+(x-200)2的值.
解:设210-x=a,x-200=b,
则ab=-204且a+b=210-x+x-200=10,
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2-2ab=102-2×(-204)=508,
即(210-x)2+(x-200)2的值为508.
仿照例题,解决问题:
若x满足(300-x)2+(302-x)2=512,试求(300-x)(302-x)的值.
解:设302-x=a,300-x=b,
∴a-b=2,
∵(a-b)2=a2-2ab+b2,a2+b2=512,
∴ab=[a2+b2-(a-b)2]=254,
即(300-x)(302-x)的值为254.
谢 谢 观 看
第18课时 十字相乘法
第十四章 整式的乘法与因式分解
一、选择题
1.对x2-3x+2分解因式,结果为( B )
A.x(x-3)+2 B.(x-1)(x-2)
C.(x-1)(x+2) D.(x+1)(x-2)
2.若多项式x2-mx+24可以分解因式,则整数m可取的值共有( D )
A.4个 B.6个 C.7个 D.8个
B
D
二、填空题
3.分解因式:
(1)ax2+2ax-3a= a(x+3)(x-1) ;
(2)(a+2)(a-2)+3a= (a-1)(a+4) ;
(3)x2-4x-12= (x-6)(x+2) ;
(4)3x2+3x-6= 3(x+2)(x-1) ;
(5)2x2-3x+1= (2x-1)(x-1) .
a(x+3)(x-1)
(a-1)(a+4)
(x-6)(x+2)
3(x+2)(x-1)
(2x-1)(x-1)
三、解答题
4.分解因式:
(1)x2-2x-15; (2)x2-10x-24;
解:原式=(x-5)(x+3)
解:原式=(x-12)(x+2)
(3)a2-15a+36; (4)x2-5xy+6y2;
解:原式=(a-12)(a-3)
解:原式=(x-2y)(x-3y)
(7)-ax2+4ax+5a.
解:原式=-a(x2-4x-5)
=-a(x-5)(x+1).
(5)x2+8xy-33y2; (6)(x+1)(x+3)-15;
解:原式=(x+11y)(x-3y)
解:原式=x2+4x+3-15
=x2+4x-12
=(x+6)(x-2).
5.把下列各式分解因式:
(1)5x2+7x-6;
解:原式=(5x-3)(x+2).
(2)3x2-7x+2;
解:原式=(3x-1)(x-2).
(3)10x2-17x+3;
解:原式=(5x-1)(2x-3).
(4)-6y2+11y+10;
解:原式=-(3y+2)(2y-5).
(5)2x2-7xy+6y2;
解:原式=(x-2y)(2x-3y).
(6)6x4-7x2+2.
解:原式=(2x2-1)(3x2-2).
一、填空题
6.若3x2+8xy-3y2=0,则代数式的值为 或-3 .
7.若x-2是x2+kx-14的一个因式,则k= 5 .
8.若x2-y2+kx+5y-6能分解为两个一次因式的积,则k的值为 ±1 .
或-3
5
±1
二、解答题
9.把下列各式分解因式:
(1)x4-10x2+9;
解:原式=(x2-1)(x2-9)
=(x+1)(x-1)(x+3)(x-3).
(2)7(x+y)3-5(x+y)2-2(x+y);
解:原式=(x+y)(7x+7y+2)(x+y-1).
(3)+22(a2+8a)+120;
解:原式=(a2+8a+12)(a2+8a+10)
=(a+2)(a+6)(a2+8a+10).
(4)(x2+2x-3)(x2+2x-24)+90;
解:原式=(x2+2x)2-27(x2+2x)+72+90
=(x2+2x)2-27(x2+2x)+162
=(x2+2x-9)(x2+2x-18).
(5)x(x+1)(x+2)(x+3)-8.
解:原式=(x2+3x)(x2+3x+2)-8
=(x2+3x)2+2(x2+3x)-8
=(x2+3x+4)(x2+3x-2).
解答题
10.阅读材料:
“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的关于x,y的二次三项式来说,方法的关键是把含x2的项的系数a分解成两个因数a1,a2的积,即a=a1a2,把含y2的项的系数c分解成两个因数c1,c2的积,即c=c1c2,并使a1c2+a2c1正好等于含xy的项的系数b,那么可以直接写出结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
解:如图1,其中1=1×1,-8=(-4)×2,而-2=1×2+1×(-4),
∴x2-2xy-8y2=(x-4y)(x+2y).
第10题图1
例:分解因式:x2-2xy-8y2.
而对于形如ax2+bxy+cy2+dx+ey+f的关于x,y的二元二次式也可以用十字相乘法来分解,如图2,把a分解成两个因数m,n作为第1列,c分解成两个因数p,q作为第2列,f分解成两个因数j,k作为第3列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,那么原式=(mx+py+j)(nx+qy+k).
第10题图2
例:分解因式:x2+2xy-3y2+3x+y+2.
解:如图3,其中1=1×1,-3=(-1)×3,2=1×2,
而2=1×3+1×(-1),1=(-1)×2+3×1,3=1×2+1×1,
∴x2+2xy-3y2+3x+y+2=(x-y+1)(x+3y+2).
第10题图3
请同学们通过上述材料,完成下列问题:
(1)分解因式:
(i)6x2-17xy+12y2= ;
(ii)2x2-xy-6y2+2x+17y-12= ;
(iii)x2-xy-6y2+2x-6y= .
(3x-4y)(2x-3y)
(x-2y+3)(2x+3y-4)
(x-3y)(x+2y+2)
(2)若关于x,y的二元二次式x2+7xy-18y2-5x+my-24可以分解成两个一次因式的积,求m的值.
或
解:(2)如图,
∴m=3×9+(-8)×(-2)=43或m=9×(-8)+3×(-2)=-78,
∴m的值为43或-78.
或
谢 谢 观 看
第19课时 复习巩固
第十四章 整式的乘法与因式分解
一、选择题
1.下列运算正确的是( D )
A.a2·a3=a6
B.(a2)3=a5
C.a6÷a2=a3
D.(a+2b)(a-2b)=a2-4b2
2.若(x-3)(x+a)=x2+bx-15,则ab的值为( A )
A.25 B.5 C.32 D.-25
D
A
3.已知3a=1,3b=2,则3a+b的值为( B )
A.1 B.2 C.3 D.27
4.若x+y=2,则多项式x2+2xy+2y2的值为( C )
A.2 B.4 C.8 D.16
5.计算52022×的结果是( C )
A.5 B.-5 C.- D.
B
C
C
二、填空题
6.(1)已知a+=5,则a2+= 23 ;
(2)若2m=a,8n=b,m、n为正整数,则23m+9n= a3b3 ;
(3)若x2+x-1=0,则代数式x3+2x2-7的值是 -6 .
23
a3b3
-6
三、解答题
7.计算:
(1)x3·xn-1-xn-2·x4+xn+2;
解:原式=xn+2-xn-2+4+xn+2
=xn+2.
(2)(m-n)2·(n-m)2÷(n-m)3;
解:原式=(n-m)4÷(n-m)3
=n-m.
(3)(x+1)2-(x-1)(x+2).
解:原式=(x2+2x+1)-(x2+x-2)
=x+3.
8.解答下列各题:
(1)已知(a+b)2=7,(a-b)2=4,求ab的值;
解:∵(a+b)2=7,(a-b)2=4,
∴ab=×[(a+b)2-(a-b)2]
=×3
=.
(2)化简求值:[4(x2+y)(x2-y)-(2x2-y)2]÷y,其中x=,y=3.
解:原式=(4x4-4y2-4x4+4x2y-y2)÷y
=(-5y2+4x2y)÷y
=-5y+4x2,
当x=,y=3时,
原式=-15+1=-14.
9.分解因式:
(1)m3(x-2)+m(2-x);
解:原式=m3(x-2)-m(x-2)
=m(x-2)(m2-1)
=m(x-2)(m+1)(m-1).
(2)25(x+y)2-36(x-y)2.
解:原式=[5(x+y)]2-[6(x-y)]2
=(5x+5y+6x-6y)(5x+5y-6x+6y)
=(11x-y)(11y-x).
一、填空题
10.我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=,则h(2)= ;
(2)如果h(1)=k(k≠0),那么h(n)·h(2023)= kn+2023 .(用含n和k的代数式表示,其中n为正整数)
11.若a=x+2021,b=x+2022,c=x+2023,则代数式2(a2+b2+c2-ab-bc-ac)的值是 6 .
kn+2023
6
二、解答题
12.已知(x-y)2=9,x2+y2=5,求[x(x2y2-xy)-y(x2-x3y)]÷x2y的值.
解:∵(x-y)2=x2+y2-2xy=9,x2+y2=5,
∴2xy=-4,即xy=-2,
∴原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y
=2(xy-1)
=-6.
13.以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)已知(x+3)2(x2+mx+n)既不含二次项,也不含一次项,求m+n的值;
解:(1)原式=(x2+6x+9)(x2+mx+n)
=x4+(m+6)x3+(6m+n+9)x2+(9m+6n)x+9n,
∵既不含二次项,也不含一次项,
∴6m+n+9=0,9m+6n=0,
解得:m=-2,n=3,
∴m+n=1;
(2)多项式M与多项式x2-3x+1的乘积为2x4+ax3+bx2+cx-3,求2a+b+c的值.
解:(2)∵多项式M与多项式x2-3x+1的乘积为2x4+ax3+bx2+cx-3,
∴设多项式M=2x2+px-3,
∴(2x2+px-3)(x2-3x+1)
=2x4-6x3+2x2+px3-3px2+px-3x2+9x-3
=2x4+(p-6)x3+(2-3p-3)x2+(p+9)x-3
=2x4+ax3+bx2+cx-3,
∴a=p-6,b=-3p-1,c=p+9,
∴2a+b+c=2p-12-3p-1+p+9=-4.
解答题
14.1261年,我国宋代数学家杨辉写了一本书《详解九章算法》,书中记载了一个用数字排成的三角形我们叫做杨辉三角(如图).
(1)请写出第五行的数字为 ;
解:(1)由规律可得出第五行的数字为1、5、10、10、5、1
第14题图
1、5、10、10、5、1
(2)第n行杨辉三角数字与(a+b)n的展开结果关系如图所示,请写出(a+b)5的展开结果;
解:(2)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
第14题图
(3)已知(a-b)1=a-b,(a-b)2=a2-2ab+b2,(a-b)3=a3-3a2b+3ab2-b3,(a-b)4=a4-4a3b+6a2b2-4ab3+b4,请写出(a-b)5的展开结果.
解:(3)(a-b)5=a5-5a4b+10a3b2-10a2b3+5ab4-b5.
谢 谢 观 看
