第十一章 三角形 习题课件(共127张PPT) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 第十一章 三角形 习题课件(共127张PPT) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 10:27:06 | ||
图片预览










文档简介
(共127张PPT)
第1课时 与三角形有关的线段(1)
第十一章 三角形
一、选择题
1.若一个三角形的两边长分别为2和4,则第三边长可能是( B )
A.2 B.4 C.6 D.8
2.一个三角形的三条边长分别为1、2、x,则x的取值范围是( D )
A.1≤x≤3 B.1<x≤3
C.1≤x<3 D.1<x<3
3.现有两根木棒分别长40cm和50cm,要从下列长度的木棒中选出一根,与前面两根木棒钉成一个三角架(木棒不能剩余),则一共可选出( A )
①5cm;②10cm;③40cm;④45cm;⑤80cm;⑥90cm.
A.3根 B.4根 C.5根 D.6根
B
D
A
二、填空题
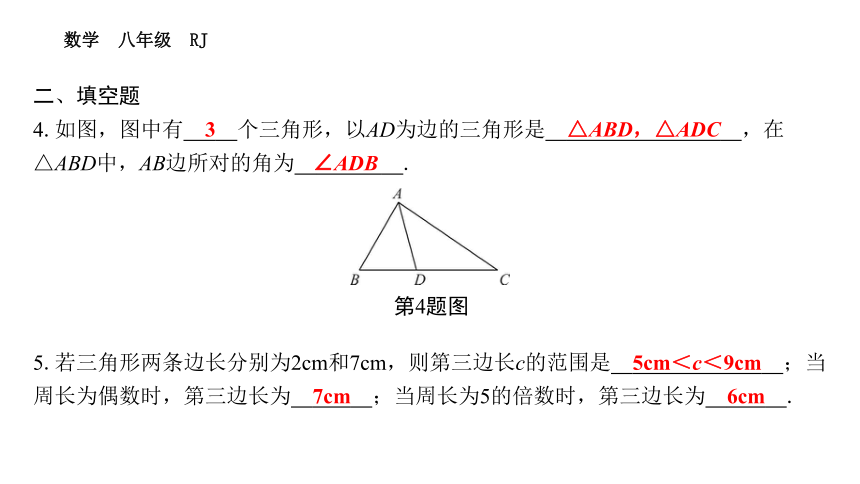
4.如图,图中有 3 个三角形,以AD为边的三角形是 △ABD,△ADC ,在△ABD中,AB边所对的角为 ∠ADB .
第4题图
5.若三角形两条边长分别为2cm和7cm,则第三边长c的范围是 5cm<c<9cm ;当周长为偶数时,第三边长为 7cm ;当周长为5的倍数时,第三边长为 6cm .
3
△ABD,△ADC
∠ADB
5cm<c<9cm
7cm
6cm
三、解答题
6.已知三角形的两边长为4和6,第三条边长x最短.
(1)求x的取值范围;
解:(1)由三角形的三边关系,得2<x<10,
∵x为最短边长,
∴x的取值范围是2<x≤4;
(2)当x为何值时,组成的三角形周长最大?最大值是多少?
解:(2)当x=4时,组成的三角形周长最大,
最大值是4+6+4=14.
7.一个等腰三角形的周长为12cm,腰与底相差3cm,求这个三角形的各边长.
解:分两种情况:
①当腰比底大3cm时,
设底边长为xcm,则腰长为(x+3)cm,
根据题意得2(x+3)+x=12,解得x=2,
∴x+3=5cm,
此时三角形的三边长分别为5cm,5cm,2cm;
②当腰比底小3cm时,
设腰长为ycm,则底边长为(y+3)cm,
根据题意得y+3+2y=12,解得y=3,
∴y+3=6cm,
∵3+3不大于6,
∴当腰比底小3cm时,组不成三角形,
综上所述,这个三角形的三边长分别为5cm,5cm,2cm.
8.已知a、b、c为△ABC的三边长,若b,c满足|c-6|=-(b-4)2,且a满足|a-4|=2,求△ABC的各边长并判断△ABC的形状.
解:∵|c-6|=-(b-4)2,
∴|c-6|+(b-4)2=0,
∴c=6,b=4,
∵|a-4|=2,∴a-4=±2,即a=6或2,
当a=6时,a,b,c分别为6,4,6,此时△ABC为等腰三角形;
当a=2时,a,b,c分别为2,4,6,
∵2+4不大于6,
∴当a=2时,以a、b、c为三边长组不成三角形,
综上所述,△ABC的三边长分别为6,4,6,△ABC为等腰三角形.
一、填空题
9.已知一个三角形的三边长分别是a、b、c,其中a和b满足方程组,若这个三角形的周长为整数,则这个三角形的周长为 9 .
9
二、解答题
10.一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm,它的周长不超过37cm,求x的取值范围.
解:∵一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm,它的周长不超过37cm,
∴,
解得:3<x≤10.
11.若△ABC的三边长分别为m-2、2m+1、8.
(1)求m的取值范围;
解:(1)根据三角形的三边关系,
得,
解得3<m<5;
(2)若△ABC的三边长均为整数,求△ABC的周长.
解:(2)∵△ABC的三边长均为整数,且3<m<5,
∴m=4,即m-2=2,2m+1=9,
∴C△ABC=2+9+8=19.
12.已知a、b、c是三角形三边长,试化简:
|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|.
解:∵a、b、c是三角形三边长,
∴b+c-a>0,b-c-a<0,c-a-b<0,a-b+c>0,
∴原式=b+c-a-b+c+a-c+a+b-a+b-c
=2b.
解答题
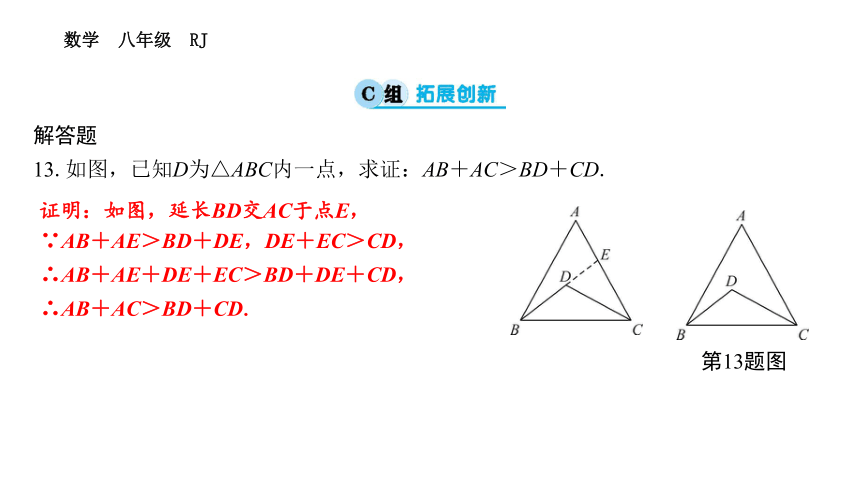
13.如图,已知D为△ABC内一点,求证:AB+AC>BD+CD.
第13题图
证明:如图,延长BD交AC于点E,
∵AB+AE>BD+DE,DE+EC>CD,
∴AB+AE+DE+EC>BD+DE+CD,
∴AB+AC>BD+CD.
谢 谢 观 看
第2课时 与三角形有关的线段(2)
第十一章 三角形
一、选择题
1.如图,已知BD=CD,则AD一定是△ABC的( C )
A.角平分线 B.高
C.中线 D.无法确定
第1题图
C
2.如图,△ABC中AC边上的高是( D )
A.线段DA B.线段BA
C.线段BC D.线段BD
第2题图
D
3.如图所示的图形中,具有稳定性的有( B )
A.1个 B.2个 C.3个 D.4个
第3题图
B
二、填空题
4.如图,在△ABC中,
第4题图
(1)若AD是△ABC的角平分线,则∠ BAD =∠ DAC =∠ BAC ;
(2)若AE是△ABC的中线,则 BE = EC = BC ;
(3)若AF是△ABC的高,则∠ AFB =∠ AFC =90°.
BAD
DAC
BAC
BE
EC
BC
AFB
AFC
5.如图,AD是△ABC的中线,AE是△ABD的中线,若S△BAE=9,则S△BAC= 36 .
第5题图
36
第6题图
6.如图,在△ABC中,AB边上的高是 CE ,BC边上的高是 AD ;在△BCF中,CF边上的高是 BC .
CE
AD
BC
三、解答题
7.(1)如图,已知△ABC和△EFD,在图中分别画出这两个三角形的三条高;
第7(1)题图
解:△ABC和△EFD的高如图所示.
(2)如图,已知△ABC.
第7(2)题图
①画中线AD;
②画△ABD的高BE及△ACD的高CF.
解:①中线AD如图所示;
②△ABD的高BE及△ACD的高CF如图所示.
8.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
第8题图
解:∵BD是△ABC的中线,
∴点D是AC的中点,
∴AC=2AD=4,
∴C△ABC=AB+BC+AC=5+4=9.
一、选择题
9.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法错误的是( C )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
第9题图
C
二、填空题
10.如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有 6 个.
第10题图
6
三、解答题
11.如图,在△ABC中,已知点D、E、F分别为BC、AD、CE的中点,若阴影部分的面积为4,求△ABC的面积.
第11题图
解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC,
∴S△BCE=S△ABC,
∵点F是CE的中点,
∴S△BEF=S△BCE=S△ABC,
∴S△ABC=4S△BEF=4×4=16.
解答题
12.△ABC中,AB∶AC=3∶2,BC=AC+1,若△ABC的中线BD把△ABC的周长分成8∶7的两部分,求边AB,AC的长.
解:由题意画出示意图如图所示,
设AB=3x,AC=2x,则BC=2x+1,
∴C△ABC=AB+AC+BC=7x+1,
分两种情况讨论:
①3x+x=(7x+1)×,
解得:x=2,
∴AB=6,AC=4;
②3x+x=(7x+1)×,
解得:x=,
∴AB=,AC=,
答:边AB的长为6,AC的长为4或边AB的长为,AC的长为.
谢 谢 观 看
第3课时 三角形的内角(1)
第十一章 三角形
一、选择题
1.在△ABC中,∠A=75°,∠B=65°,则下列关于∠C的说法正确的是( A )
A.它等于40° B.它等于50°
C.它是个直角 D.它是个钝角
2.已知∠A∶∠B∶∠C=1∶2∶2,则△ABC三个内角的度数分别是( D )
A.40°、80°、80° B.35°、70°、70°
C.30°、60°、60° D.36°、72°、72°
3.已知△ABC中,2(∠B+∠C)=3∠A,则∠A的度数是( B )
A.54° B.72° C.108° D.144°
A
D
B
二、填空题
4.(1)在△ABC中,若∠C=80°,∠A=30°,则∠B= 70° ;
(2)在△ABC中,若∠A=40°,∠B=∠C,则∠B= 70° .
70°
70°
三、解答题
5.已知在△ABC中,∠A=2∠B,∠C=∠B+20°,求△ABC的各内角度数.
解:∵∠A+∠B+∠C=180°,
∠A=2∠B,∠C=∠B+20°,
∴2∠B+∠B+∠B+20°=180°,
∴∠B=40°,
∴∠A=2∠B=80°,∠C=∠B+20°=60°.
6.如图,在△ABC中,CE平分∠ACB,∠1=∠2,若∠ACE=23°,求∠EDC的度数.
第6题图
解:∵CE平分∠ACB,∠ACE=23°,
∴∠1=∠ACE=23°,
∵∠1=∠2,∴∠2=23°,
∵∠EDC+∠2+∠1=180°,
∴∠EDC=180°-(∠2+∠1)=134°.
7.如图,在△ABC中,∠A=50°,∠ABD=35°,∠ACB=70°,且CE平分∠ACB,求∠BEC的度数.
第7题图
解:∵∠A=50°,∠ACB=70°,
∴∠ABC=180°-∠A-∠ACB=60°,
∵∠ABD=35°,
∴∠CBD=∠ABC-∠ABD=25°,
∵CE平分∠ACB,
∴∠BCE=∠ACB=35°,
∴在△BCE中,∠BEC=180°-∠CBD-∠BCE=120°.
8.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,求∠C的度数.
第8题图
解:如图,
由题意得∠BAE=45°,∠CAE=15°,∠DBC=85°,
∵AE∥BD,∴∠DBA=∠BAE=45°,
∴∠ABC=∠DBC-∠DBA=40°,∠BAC=∠BAE+∠CAE=60°,
由三角形的内角和定理,得:
∠C=180°-∠BAC-∠ABC=80°.
一、填空题
9.设三角形的三个内角分别为α、β、γ,且α≥β≥γ,α=2γ,则β的最大值与最小值的和是 117° .
10.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC上,点G在DE的延长线上,连接GF,且∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为 70° .
117°
70°
第10题图
二、解答题
11.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的点A'处,折痕为DE.已知∠BDA'=110°,∠C=70°,∠B=80°,设∠CFD=α,∠CEA'=β,求α和β的度数.
第11题图
解:∵∠C=70°,∠B=80°,
∴∠A=180°-∠B-∠C=30°,
∵∠BDA'=110°,
∴∠ADA'=180°-∠BDA'=70°,
∴∠AFD=180°-∠ADA'-∠A=80°,
∴α=180°-∠AFD=100°,
∴∠A'FE=α=100°,
由折叠可知,∠A'=∠A=30°,
∴β=180°-∠A'-∠A'FE=50°.
解答题
12.如图,BD、CE相交于点A,连接CB,DE.
(1)探索∠B、∠C、∠D、∠E之间的数量关系,并说明理由;
解:(1)∠B+∠C=∠D+∠E,理由如下:
∵∠B+∠C+∠BAC=180°,∠D+∠E+∠DAE=180°,∠BAC=∠DAE,
∴∠B+∠C=∠D+∠E;
第12题图
(2)若∠BCE、∠BDE的角平分线相交于点O,利用(1)中的结论探索∠B、∠E、∠O之间的数量关系,并说明理由.
解:(2)∠B+∠E=2∠O,理由如下:
如图,
第12题图
类似于(1)中的结论,有:
∠B+∠BCO=∠O+∠BDO,
而∠BCO=∠BCA,∠BDO=∠BDE,
∴∠O=∠B+(∠BCA-∠BDE),
∵∠B+∠BCA=∠E+∠BDE,
∴∠BCA-∠BDE=∠E-∠B,
∴∠O=∠B+(∠E-∠B),
∴∠B+∠E=2∠O.
谢 谢 观 看
第4课时 三角形的内角(2)
第十一章 三角形
一、选择题
1.在一个直角三角形中,有一个锐角为35°,则另一个锐角的度数是( C )
A.75° B.65° C.55° D.45°
2.如图,△ABC中,∠C=90°,则∠B=( D )
A.15° B.30° C.50° D.60°
第2题图
C
D
3.如图,已知在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( B )
A.90° B.20° C.45° D.70°
第3题图
B
第4题图
4.如图,在△ABC中,∠ACB=90°,过点C作CD∥AB交∠ABC的平分线于点D,若∠ABD=20°,则∠ACD的度数为( D )
D
A.20° B.30° C.40° D.50°
二、填空题
5.在Rt△ABC中,∠C=90°,∠A=70°,则∠B= 20° .
6.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为点E.若∠CAD=20°,则∠EDB的度数是 40° .
第6题图
20°
40°
三、解答题
7.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD的延长线于点E.若∠DBE=28°,求∠CAB的度数.
第7题图
解:∵BE⊥AE,
∴∠E=90°=∠C,
∵∠ADC=∠BDE,
∴∠CAD=∠DBE=28°,
∵AE平分∠CAB,
∴∠CAB=2∠CAD=56°.
8.如图,在Rt△ABC中,∠C=90°,∠CAB、∠CBA的角平分线AD、BE交于点F,求∠AFB的度数.
第8题图
解:∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵AD平分∠CAB,BE平分∠CBA,
∴∠FAB=∠CAB,∠FBA=∠CBA,
∴∠FAB+∠FBA=(∠CAB+∠CBA)=45°,
∴∠AFB=180°-(∠FAB+∠FBA)=135°.
9.如图,AB、ED分别垂直于BD,点B、D是垂足,且∠ACB=∠CED.求证:△ACE是直角三角形.
第9题图
证明:∵ED⊥BD,
∴∠CDE=90°,
∴∠CED+∠DCE=90°,
∵∠ACB=∠CED,
∴∠ACB+∠DCE=90°,
∴∠ACE=180°-(∠ACB+∠DCE)=90°,
∴△ACE是直角三角形.
一、选择题
10.如图,CD是Rt△ABC斜边AB上的高,且CB>CA,图中相等的角共有( D )
A.2对 B.3对 C.4对 D.5对
第10题图
D
11.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上的点E处,若∠A=25°,则∠ADE的度数为( A )
A.40° B.50° C.65° D.75°
第11题图
A
二、解答题
12.如图,在△ABC中,∠A=30°,∠B=60°,CE平分∠ACB,点F在CE上.
(1)求∠ACE的度数;
(1)解:∵∠A=30°,∠B=60°,
∴∠ACB=180°-∠A-∠B=90°,
又∵CE平分∠ACB,
∴∠ACE=∠ACB=45°;
第12题图
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
(2)证明:∵CD⊥AB,∠B=60°,
∴∠BCD=90°-∠B=30°,
又∵∠BCE=∠ACE=45°,
∴∠DCF=∠BCE-∠BCD=15°,
又∵∠CDF=75°,
∴∠CFD=180°-∠CDF-∠DCF=90°,
∴△CFD是直角三角形.
第12题图
解答题
13.如图,已知在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数;
解:(1)∵∠B=70°,∠C=30°,
∴∠BAC=180°-∠B-∠C=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°;
第13题图
(2)求∠DAE的度数;
解:(2)∵AD⊥BC,∴∠ADE=∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠BAD=90°-∠B=20°,
∴∠DAE=∠BAE-∠BAD=20°;
第13题图
解:(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C),
∵AD⊥BC,∴∠ADB=90°,
∴∠B+∠BAD=90°,∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-(∠B+∠C)-(90°-∠B)=(∠B-∠C),
第13题图
(3)探究:如果将条件“∠B=70°,∠C=30°”改成“∠B-∠C=40°”,能否得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
∵∠B-∠C=40°,
∴∠DAE=×40°=20°.
谢 谢 观 看
第5课时 三角形的外角
第十一章 三角形
一、选择题
1.如图,已知∠ACD=130°,∠B=20°,则∠A的度数是( A )
A.110° B.130° C.150° D.90°
第1题图
2.将一副直角三角板按如图所示的方式叠放,则∠1的度数为( A )
A.105° B.100° C.95° D.110°
第2题图
A
A
3.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( D )
A.75° B.105° C.135° D.165°
第3题图
D
4.如图,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,若∠ABP=20°,∠ACP=50°,则∠A=( A )
A.60° B.80° C.70° D.50°
第4题图
A
二、填空题
5.△ABC中,∠B=65°,∠A比∠C小35°,则与∠C相邻的外角的度数为 105° .
6.如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2= 101° .
第6题图
105°
101°
三、解答题
7.如图,已知D为BC上一点,∠B=∠1,∠BAC=64°,求∠2的度数.
第7题图
解:∵∠BAC=64°,
∴∠BAD+∠1=64°,
∵∠B=∠1,
∴∠B+∠BAD=64°,
∵∠2是△ABD的外角,
∴∠2=∠B+∠BAD=64°.
8.如图,若∠A=27°,∠B=45°,∠C=38°,求∠DFE的度数.
第8题图
解:∵∠A=27°,∠C=38°,
∴∠AEB=∠A+∠C=65°,
∵∠B=45°,
∴∠DFE=∠B+∠BEF=110°.
9.如图,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC,求∠4的度数.
第9题图
解:∵∠1=100°,∠C=80°,
∴∠3=∠1-∠C=20°,
∵∠2=∠3,∴∠2=10°,
∴∠ABC=180°-∠1-∠2=70°,
∵BE平分∠ABC,∴∠ABE=∠ABC=35°,
∵∠4=∠2+∠ABE,
∴∠4=45°.
一、填空题
10.如图,∠CAD和∠CBD的平分线相交于点P.设∠CAD、∠CBD、∠C、∠D的度数依次为a、b、c、d,用仅含其中2个字母的代数式来表示∠P的度数为 .
第10题图
二、解答题
11.如图,点D、E分别在AC、AB上,BD、CE交于点F,∠B∶∠C=3∶2.
(1)若∠A=60°,∠DFE=100°,求∠BEC的度数;
解:(1)设∠B=3x,则∠C=2x,
∵∠DFE=∠FDC+∠C,∠FDC=∠A+∠B,
∴∠DFE=∠C+∠A+∠B,
即3x+2x+60°=100°,解得x=8°,
∴∠B=24°,∠C=16°,
∴∠BEC=∠A+∠C=76°;
第11题图
(2)若∠DFE-∠A=130°,求∠B的度数.
解:(2)∵∠DFE=∠C+∠A+∠B,
∴∠DFE-∠A=∠C+∠B,
∴3x+2x=130°,解得x=26°,
∴∠B=78°.
第11题图
解答题
12.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠P= ;
122°
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E,其中∠A=α,求∠E的度数;(用含α的代数式表示)
解:(2)如图,∵CE平分∠ACB,BE平分∠ABD,
∴∠1=∠ACB,∠2=∠ABD,
又∵∠ABD=∠A+∠ACB,
∴∠2=∠A+∠1,
∴∠E=∠2-∠1=∠A+∠1-∠1=;
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠Q与∠A的数量关系,并证明.
解:(3)∠Q=90°-∠A,
证明:∵BQ平分∠CBM,CQ平分∠BCN,
∴∠QBC=(∠A+∠ACB),∠QCB=(∠A+∠ABC),
∴∠Q=180°-∠QBC-∠QCB
=180°-(∠A+∠ACB)-(∠A+∠ABC)
=180°-∠A-(∠A+∠ABC+∠ACB)
=180°-∠A-90°
=90°-∠A.
谢 谢 观 看
第6课时 专题与角平分线有关的三角形内角和问题
第十一章 三角形
一、选择题
1.如图,点O是△ABC内一点,∠A= 80°,BO、CO分别是∠ABC、∠ACB的角平分线,则∠BOC的度数为( C )
A.140° B.135° C.130° D.125°
第1题图
C
2.如图,BP、CP分别为∠ABC、∠ACE的角平分线,若∠A= 45°,则∠P的度数是( B )
A.20° B.22.5° C.25° D.30°
第2题图
B
二、填空题
3.如图,在△ABC中,点O是∠ABC和∠ACB的平分线的交点,点E,D分别是OB,OC延长线上的点,∠CBE和∠BCD的平分线交于点P,∠A=α,则∠P的度数为 45°-α .(用含α的代数式表示)
第3题图
45°-α
三、解答题
4.如图,已知△OAB中,∠O=70°,∠OAB的平分线与△OBA的外角∠ABN的平分线所在的直线交于点D,求∠ADB的度数.
第4题图
解:∵AD平分∠OAB,
BC平分∠ABN,
∴∠ABC=∠ABN,
∠BAD=∠OAB,
∴∠ADB=∠ABC-∠BAD=(∠ABN-∠OAB)=∠O=35°.
5.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数.
第5题图
解:∵AD是BC上的高,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°-∠C=20°,
∵∠BAC=50°,AE平分∠BAC,
∴∠ABC=180°-∠BAC-∠C=60°,∠BAO=∠BAC=25°,
∵BF平分∠ABC,∴∠ABO=∠ABC=30°,
∴∠AOB=180°-∠ABO-∠BAO=125°.
6.如图所示,在△ABC中,∠A=40°,BP、CP是△ABC的外角平分线,求∠P的度数.
第6题图
解:∵BP、CP是△ABC的外角平分线,
∴∠PBC+∠PCB=(∠A+∠ACB+∠A+∠ABC)=110°,
∴∠P=180°-(∠PBC+∠PCB)=70°.
一、选择题
7.如图,△ABC中,∠ABD=∠DBE=∠EBC,∠ACD=∠DCE=∠ECB,若∠BEC=145°,则∠BDC的度数为( D )
A.80° B.90° C.100° D.110°
第7题图
D
二、填空题
8.如图,AB∥CD,∠1=∠2,BC交AD于点E.
(1)如图1,若AD⊥BD于点D,∠DAB=40°,则∠3的度数为 25 °;
25
(2)如图2,∠BAD与∠BDF的平分线交于点P,若∠ADB=70°,则∠P的度数为 55 °.
55
三、解答题
9.在△ABC中,若存在一个内角角度是另外一个内角角度的n倍(n为大于1的正整数),则称△ABC为n倍角三角形.例如,在△ABC中,∠A=80°,∠B=75°,∠C=25°,可知∠B=3∠C,故△ABC为3倍角三角形.
(1)在△ABC中,∠A=80°,∠B=60°,则△ABC为 倍角三角形;
2
(2)若锐角△MNP是3倍角三角形,且最小内角为α,则α的范围为 ;
22.5°<α<30°
(3)如图,直线MN与直线PQ垂直相交于点O,点A在射线OP上运动(点A不与点O重合),点B在射线OM上运动(点B不与点O重合).延长BA至点G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于点E、F,若△AEF为4倍角三角形,求∠ABO的度数.
第9(3)题图
解:(3)∵AE平分∠BAO,AF平分∠OAG,
∴∠EAB=∠EAO,∠OAF=∠FAG,
∴∠EAF=∠EAO+∠OAF=(∠BAO+∠OAG)=90°,
∵△EAF是4倍角三角形,∠F>∠E,
∴∠E=×90°或×90°,即∠E=22.5°或18°,
∵OE平分∠BOQ,∴∠E=∠ABO,
∴∠ABO=2∠E=45°或36°.
解答题
10.如图1,直线m与直线n相交于点O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO、∠ABO的角平分线.
(1)若∠BAO=50°,∠ABO=40°,求∠ACB的度数;
解:(1)∵AC、BC分别是∠BAO、∠ABO的角平分线,
∴∠CAB=∠BAO=25°,∠CBA=∠ABO=20°,
∴∠ACB=180°-∠CAB-∠CBA=135°;
(2)如图2,若∠AOB=α,BD是△AOB的外角∠OBE的角平分线,BD与AC延长线交于点D,点A、B在运动的过程中,∠ADB的度数是否发生变化?若发生变化,请说明理由;若不发生变化,试求出其度数(用含α的代数式表示);
解:(2)∠ADB的度数不发生变化,
∵AC平分∠BAO,BD平分∠OBE,
∴∠BAD=∠BAO,∠EBD=∠OBE,
∴∠ADB=∠EBD-∠BAD=(∠OBE-∠BAO)=∠AOB=α;
(3)如图3,若直线m与直线n相互垂直,延长AB至E,已知∠OBE、∠ABO的角平分线与∠BOQ的角平分线及其延长线分别相交于点D、F,在△BDF中,如果有一个角是另一个角的3倍,请直接写出∠BAO的度数.
解:(3)∠BAO=60°或45°.
谢 谢 观 看
第7课时 多边形
第十一章 三角形
一、选择题
1.下列图形中是多边形的是( D )
A
B
C
D
2.下列图形中∠1是外角的是( D )
A
B
C
D
D
D
3.下列说法正确的是( B )
A.一个多边形外角的个数与边数相同
B.一个多边形外角的个数是边数的二倍
C.每个角都相等的多边形是正多边形
D.每条边都相等的多边形是正多边形
4.如图所示的图形中,矩形的个数是( D )
A.3个 B.4个 C.5个 D.6个
第4题图
B
D
5.长方形剪去一个角后所得的图形一定不是( C )
A.五边形 B.梯形 C.长方形 D.三角形
C
二、填空题
6.如图所示,将多边形分割成三角形,①中可分割出2个三角形,②中可分割出3个三角形,③中可分割出4个三角形,…,由此能猜测出n边形可以分割出 (n-1) 个三角形.
第6题图
(n-1)
第7题图
7.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为 4 .
4
三、解答题
8.画出下列多边形的全部对角线.
第8题图
解:如图所示:
9.一个四边形的周长是46cm,已知第一条边的边长是acm,第二条边的边长比第一条边的边长的三倍少5cm,第三条边的边长等于第一、第二条边的边长之和.
(1)请用含a的式子表示第四条边的边长;
解:(1)由题意得:第二条边的边长为(3a-5)cm,第三条边的边长为a+3a-5=(4a-5)cm,
则第四条边的边长为46-a-(3a-5)-(4a-5)=(56-8a)cm,
答:第四条边的边长为(56-8a)cm;
(2)当a=7时还能得到四边形吗?为什么?此时的图形是什么形状?
解:(2)当a=7时不能得到四边形,理由如下:
∵此时第四条边的边长为56-8a=0cm,只剩下三条边,
∴三条边的边长分别为a=7cm,3a-5=16cm,4a-5=23cm,
∵7+16=23cm,∴图形是线段,
答:当a=7时不能得到四边形,此时的图形是线段.
一、选择题
10.若一个多边形截去一个角后,变成十五边形,则原来的多边形的边数为( A )
A.14或15或16 B.15或16
C.14或16 D.15或16或17
A
二、填空题
11.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k条对角线,则(m-k)n的值是 125 .
125
三、解答题
12.已知正n边形的周长为60,边长为a.
(1)当n=3时,请直接写出a的值;
解:(1)a=60÷3=20;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n=3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若对,请给出证明;若不对,请求出不符合这一说法的n的值.
解:(2)这种说法不对.
令a=b,得=,
∴60n+420=67n,
解得n=60,
∴当n=60时,a=b,
即不符合这一说法的n的值为60.
解答题
13.阅读材料:
我们知道计算n边形的对角线条数公式为,如果有一个n边形的对角线一共有20条,那么可以得到方程=20,去分母得n(n-3)=40,由于n为大于等于3的整数,且n比n-3的值大3,所以满足积为40且相差3的因数只有8和5,符合方程的整数解为n=8,即多边形是八边形.根据材料内容,回答下列问题:
(1)若有一个多边形的对角线一共有14条,求这个多边形的边数;
解:(1)由题意得,=14,
去分母得:n(n-3)=28,
∵n为大于等于3的整数,且n比n-3的值大3,
∴满足积为28且相差3的因数只有7和4,
符合方程的整数解为n=7,
即这个多边形的边数为7;
(2)A同学说:“我求得一个多边形的对角线一共有30条.”你认为A同学的说法正确吗?为什么?
解:(2)A同学的说法不正确,理由如下:
∵=30,去分母得n(n-3)=60,
当n=9时,n(n-3)=9×6=54<60,
当n=10时,n(n-3)=10×7=70>60,
∴符合方程的正整数n不存在,即多边形的对角线不可能有30条,
∴A同学的说法不正确.
谢 谢 观 看
第8课时 多边形的内角和
第十一章 三角形
一、选择题
1.内角和为540°的多边形是( C )
A.三角形 B.四边形 C.五边形 D.六边形
2.已知一个正多边形的一个内角为150度,则它的边数为( A )
A.12 B.9 C.8 D.7
3.一个正多边形,它的一个内角恰好是一个外角的4倍,则这个正多边形的边数是( C )
A.8 B.9 C.10 D.12
C
A
C
4.如图,在一个三角形纸片ABC中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为( C )
A.90° B.180° C.270° D.315°
第4题图
C
二、填空题
5.九边形的内角和为 1260° ,从一个顶点出发有 6 条对角线,共有 27 条对角线.
6.如图,已知∠1+∠2+∠3=310°,则∠4= 50° .
第6题图
1260°
6
27
50°
三、解答题
7.已知一个多边形的内角和与外角和之比是3∶2,求这个多边形的边数.
解:设这个多边形的边数为n,
依题意得:(n-2)×180°=×360°,
解得n=5,
∴这个多边形的边数为5.
8.如图,若正五边形ABCDE和长方形AFCG按如图方式叠放在一起,求∠EAF的度数.
第8题图
解:∵正五边形内角和为540°,
∴其每个内角为540°÷5=108°,
∵长方形每个内角为90°,∴∠F=90°,
∴∠ABC=108°,∠ABF=180°-∠ABC=72°,
∴∠BAF=180°-∠F-∠ABF=18°,
∴∠EAF=∠EAB+∠BAF=126°.
9.如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(1)解:∵六边形ABCDEF的各内角相等,
∴一个内角的度数为=120°,
∴∠E=∠F=∠FAB=120°,
∵∠1=48°,
∴∠FAD=∠FAB-∠1=72°,
∵∠2+∠FAD+∠F+∠E=360°,
∴∠2=360°-∠FAD-∠F-∠E=48°;
第9题图
(2)求证:AB∥DE.
(2)证明:由(1)知∠E=∠F=∠FAB=120°,
∴∠1=∠FAB-∠DAF=120°-∠DAF,
∠2=360°-∠E-∠F-∠DAF=120°-∠DAF,
∴∠1=∠2,∴AB∥DE.
第9题图
一、选择题
10.如图,在正五边形ABCDE中,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G=( B )
A.36° B.54° C.60° D.72°
第10题图
B
二、填空题
11.已知一个多边形,少算一个内角的度数,其余内角和为2100°,则这个多边形的边数为 14 .
14
三、解答题
12.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
第12题图
解:如图,连接CG,
∵∠COG=∠AOB,
∴∠6+∠7=∠OCG+∠OGC,
又∵在五边形CDEFG中,
∠1+∠2+∠OCG+∠OGC+∠3+∠4+∠5=(5-2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
解答题
13.(1)如图1,在△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的平分线交于点D,若∠ABC=75°,∠ACB=45°,求∠D的度数;
解:(1)∵BD平分∠ABC,CD平分∠ACE,
∴∠DBC=∠ABC,∠DCE=∠ACE,
∵∠ACE=∠ABC+∠A,
∠DCE=∠DBC+∠D,
∴∠DCE=∠ACE=(∠ABC+∠A),
即∠DBC+∠D=(∠ABC+∠A),
∴∠D=∠A,
∵∠ABC=75°,∠ACB=45°,
∴∠A=180°-∠ABC-∠ACB=60°,
∴∠D=∠A=30°;
(2)如图2,在四边形MNCB中,BD平分∠MBC,且与四边形MNCB的外角∠NCE的平分线交于点D,若∠BMN=130°,∠CNM=100°,求∠D的度数.
解:(2)如图,延长BM,CN交于点A,
∵∠BMN=∠ANM+∠A,
∠CNM=∠AMN+∠A=180°-∠ANM,
∴∠A=∠BMN+∠CNM-180°=50°,
由(1)知∠D=∠A,
∴∠D=25°.
谢 谢 观 看
第9课时 复习巩固
第十一章 三角形
一、选择题
1.以下列长度的各组线段为边,能组成三角形的是( D )
A.2cm,3cm,5cm B.3cm,3cm,6cm
C.5cm,8cm,2cm D.4cm,5cm,6cm
2.已知正多边形的一个内角是135°,则这个正多边形的边数是( D )
A.3 B.4 C.6 D.8
D
D
3.如图,AM是△ABC的中线,△ABC的面积为4cm2,则△ABM的面积为( C )
A.8cm2 B.4cm2
C.2cm2 D.以上答案都不对
第3题图
C
二、填空题
4.如图,在△ABC中,AD是角平分线,AE是中线,AF是高.如果BC=10cm,那么BE= 5cm ;如果∠ABC=40°,∠ACB=60°,那么∠BAD= 40° ,∠DAF= 10° .
第4题图
5.三角形三个内角度数之比是1∶1∶2,则这个三角形是 等腰直角 三角形.
5cm
40°
10°
等腰直角
6.若从一个多边形的一个顶点出发可以引5条对角线,则这个多边形的内角和为 1080° .
7.如图,五边形ABCDE的每一个内角都相等,则外角∠CBF= 72° .
第7题图
1080°
72°
三、解答题
8.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是△ABC内部的一条线段,AE交CD于点F,交CB于点E,且∠CFE=∠CEF.求证:AE平分∠CAB.
第8题图
证明:∵CD⊥AB,
∴在Rt△ADF中,
∠DAF=90°-∠AFD=90°-∠CFE,
∵∠ACE=90°,
∴在Rt△AEC中,∠CAE=90°-∠CEF,
∵∠CFE=∠CEF,
∴∠DAF=∠CAE,
即AE平分∠CAB.
9.如图,在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40的两部分,求AC和AB的长.
第9题图
解:∵AD是BC边上的中线,
∴BD=CD,
∵AC>AB,
∴AC+CD=60,AB+BD=40,
设BD=CD=x,AB=y,则AC=2BC=4x,
∴4x+x=60,x+y=40,
解得:x=12,y=28,
∴AC=4x=48,AB=28.
一、填空题
10.如图,△ABC的三条中线AD,BE,CF交于点G,若S△ABC=12,则图中阴影部分的面积是 4 .
第10题图
4
二、解答题
11.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获.如图所示的两幅图都是由同一副直角三角板拼凑得到的.
(1)如图1,求∠ABC的度数;
解:(1)∵∠F=30°,∠EAC=45°,
∴∠ABF=∠EAC-∠F=15°,
∵∠FBC=90°,
∴∠ABC=∠FBC-∠ABF=75°;
(2)如图2,若AE∥BC,求∠AFD的度数.
解:(2)∵∠B=60°,∠BAC=90°,∴∠C=30°,
∵AE∥BC,∴∠CAE=∠C=30°,
∴∠AFD=∠CAE+∠E=75°.
解答题
12.如图1,点D为△ABC内一点,连接BD,CD.
第12题图1
(1)探究∠BDC与∠A,∠ABD,∠ACD之间的关系,并说明理由;
解:(1)∠BDC=∠A+∠ABD+∠ACD,
理由:如图,连接AD并延长交BC于点E,
∵∠BDE=∠BAE+∠ABD,
∠EDC=∠EAC+∠ACD,
∴∠BDE+∠EDC=∠BAE+∠EAC+∠ABD+∠ACD,
∴∠BDC=∠BAC+∠ABD+∠ACD;
(2)请直接用(1)中的结论,解决下列问题:
①当∠BDC=120°时,若∠A=50°,则∠ABD+∠ACD= °;
②如图2,BE平分∠ABD,CE平分∠ACD,若∠BDC=120°,∠A=50°,求∠BEC的度数;
③如图3,∠ABD,∠ACD的n等分线相交于点E1,E2,…,En-1,若∠BDC=x°,∠BE1C=y°,求∠A的度数.(用含x,y,n的式子表示)
70
解:(2)②∵BE平分∠ABD,CE平分∠ACD,
∴∠ABE=∠ABD,∠ACE=∠ACD,
∴∠BEC=∠ABE+∠ACE+∠A=(∠ABD+∠ACD)+∠A
=×(∠BDC-∠A)+50°=85°;
③以此类推(∠BDC-∠A)+∠A=∠BE1C,
即(x°-∠A)+∠A=y°,
则∠A=.
谢 谢 观 看
第1课时 与三角形有关的线段(1)
第十一章 三角形
一、选择题
1.若一个三角形的两边长分别为2和4,则第三边长可能是( B )
A.2 B.4 C.6 D.8
2.一个三角形的三条边长分别为1、2、x,则x的取值范围是( D )
A.1≤x≤3 B.1<x≤3
C.1≤x<3 D.1<x<3
3.现有两根木棒分别长40cm和50cm,要从下列长度的木棒中选出一根,与前面两根木棒钉成一个三角架(木棒不能剩余),则一共可选出( A )
①5cm;②10cm;③40cm;④45cm;⑤80cm;⑥90cm.
A.3根 B.4根 C.5根 D.6根
B
D
A
二、填空题
4.如图,图中有 3 个三角形,以AD为边的三角形是 △ABD,△ADC ,在△ABD中,AB边所对的角为 ∠ADB .
第4题图
5.若三角形两条边长分别为2cm和7cm,则第三边长c的范围是 5cm<c<9cm ;当周长为偶数时,第三边长为 7cm ;当周长为5的倍数时,第三边长为 6cm .
3
△ABD,△ADC
∠ADB
5cm<c<9cm
7cm
6cm
三、解答题
6.已知三角形的两边长为4和6,第三条边长x最短.
(1)求x的取值范围;
解:(1)由三角形的三边关系,得2<x<10,
∵x为最短边长,
∴x的取值范围是2<x≤4;
(2)当x为何值时,组成的三角形周长最大?最大值是多少?
解:(2)当x=4时,组成的三角形周长最大,
最大值是4+6+4=14.
7.一个等腰三角形的周长为12cm,腰与底相差3cm,求这个三角形的各边长.
解:分两种情况:
①当腰比底大3cm时,
设底边长为xcm,则腰长为(x+3)cm,
根据题意得2(x+3)+x=12,解得x=2,
∴x+3=5cm,
此时三角形的三边长分别为5cm,5cm,2cm;
②当腰比底小3cm时,
设腰长为ycm,则底边长为(y+3)cm,
根据题意得y+3+2y=12,解得y=3,
∴y+3=6cm,
∵3+3不大于6,
∴当腰比底小3cm时,组不成三角形,
综上所述,这个三角形的三边长分别为5cm,5cm,2cm.
8.已知a、b、c为△ABC的三边长,若b,c满足|c-6|=-(b-4)2,且a满足|a-4|=2,求△ABC的各边长并判断△ABC的形状.
解:∵|c-6|=-(b-4)2,
∴|c-6|+(b-4)2=0,
∴c=6,b=4,
∵|a-4|=2,∴a-4=±2,即a=6或2,
当a=6时,a,b,c分别为6,4,6,此时△ABC为等腰三角形;
当a=2时,a,b,c分别为2,4,6,
∵2+4不大于6,
∴当a=2时,以a、b、c为三边长组不成三角形,
综上所述,△ABC的三边长分别为6,4,6,△ABC为等腰三角形.
一、填空题
9.已知一个三角形的三边长分别是a、b、c,其中a和b满足方程组,若这个三角形的周长为整数,则这个三角形的周长为 9 .
9
二、解答题
10.一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm,它的周长不超过37cm,求x的取值范围.
解:∵一个三角形的三边长分别是xcm、(x+2)cm、(x+5)cm,它的周长不超过37cm,
∴,
解得:3<x≤10.
11.若△ABC的三边长分别为m-2、2m+1、8.
(1)求m的取值范围;
解:(1)根据三角形的三边关系,
得,
解得3<m<5;
(2)若△ABC的三边长均为整数,求△ABC的周长.
解:(2)∵△ABC的三边长均为整数,且3<m<5,
∴m=4,即m-2=2,2m+1=9,
∴C△ABC=2+9+8=19.
12.已知a、b、c是三角形三边长,试化简:
|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|.
解:∵a、b、c是三角形三边长,
∴b+c-a>0,b-c-a<0,c-a-b<0,a-b+c>0,
∴原式=b+c-a-b+c+a-c+a+b-a+b-c
=2b.
解答题
13.如图,已知D为△ABC内一点,求证:AB+AC>BD+CD.
第13题图
证明:如图,延长BD交AC于点E,
∵AB+AE>BD+DE,DE+EC>CD,
∴AB+AE+DE+EC>BD+DE+CD,
∴AB+AC>BD+CD.
谢 谢 观 看
第2课时 与三角形有关的线段(2)
第十一章 三角形
一、选择题
1.如图,已知BD=CD,则AD一定是△ABC的( C )
A.角平分线 B.高
C.中线 D.无法确定
第1题图
C
2.如图,△ABC中AC边上的高是( D )
A.线段DA B.线段BA
C.线段BC D.线段BD
第2题图
D
3.如图所示的图形中,具有稳定性的有( B )
A.1个 B.2个 C.3个 D.4个
第3题图
B
二、填空题
4.如图,在△ABC中,
第4题图
(1)若AD是△ABC的角平分线,则∠ BAD =∠ DAC =∠ BAC ;
(2)若AE是△ABC的中线,则 BE = EC = BC ;
(3)若AF是△ABC的高,则∠ AFB =∠ AFC =90°.
BAD
DAC
BAC
BE
EC
BC
AFB
AFC
5.如图,AD是△ABC的中线,AE是△ABD的中线,若S△BAE=9,则S△BAC= 36 .
第5题图
36
第6题图
6.如图,在△ABC中,AB边上的高是 CE ,BC边上的高是 AD ;在△BCF中,CF边上的高是 BC .
CE
AD
BC
三、解答题
7.(1)如图,已知△ABC和△EFD,在图中分别画出这两个三角形的三条高;
第7(1)题图
解:△ABC和△EFD的高如图所示.
(2)如图,已知△ABC.
第7(2)题图
①画中线AD;
②画△ABD的高BE及△ACD的高CF.
解:①中线AD如图所示;
②△ABD的高BE及△ACD的高CF如图所示.
8.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
第8题图
解:∵BD是△ABC的中线,
∴点D是AC的中点,
∴AC=2AD=4,
∴C△ABC=AB+BC+AC=5+4=9.
一、选择题
9.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法错误的是( C )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
第9题图
C
二、填空题
10.如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有 6 个.
第10题图
6
三、解答题
11.如图,在△ABC中,已知点D、E、F分别为BC、AD、CE的中点,若阴影部分的面积为4,求△ABC的面积.
第11题图
解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC,
∴S△BCE=S△ABC,
∵点F是CE的中点,
∴S△BEF=S△BCE=S△ABC,
∴S△ABC=4S△BEF=4×4=16.
解答题
12.△ABC中,AB∶AC=3∶2,BC=AC+1,若△ABC的中线BD把△ABC的周长分成8∶7的两部分,求边AB,AC的长.
解:由题意画出示意图如图所示,
设AB=3x,AC=2x,则BC=2x+1,
∴C△ABC=AB+AC+BC=7x+1,
分两种情况讨论:
①3x+x=(7x+1)×,
解得:x=2,
∴AB=6,AC=4;
②3x+x=(7x+1)×,
解得:x=,
∴AB=,AC=,
答:边AB的长为6,AC的长为4或边AB的长为,AC的长为.
谢 谢 观 看
第3课时 三角形的内角(1)
第十一章 三角形
一、选择题
1.在△ABC中,∠A=75°,∠B=65°,则下列关于∠C的说法正确的是( A )
A.它等于40° B.它等于50°
C.它是个直角 D.它是个钝角
2.已知∠A∶∠B∶∠C=1∶2∶2,则△ABC三个内角的度数分别是( D )
A.40°、80°、80° B.35°、70°、70°
C.30°、60°、60° D.36°、72°、72°
3.已知△ABC中,2(∠B+∠C)=3∠A,则∠A的度数是( B )
A.54° B.72° C.108° D.144°
A
D
B
二、填空题
4.(1)在△ABC中,若∠C=80°,∠A=30°,则∠B= 70° ;
(2)在△ABC中,若∠A=40°,∠B=∠C,则∠B= 70° .
70°
70°
三、解答题
5.已知在△ABC中,∠A=2∠B,∠C=∠B+20°,求△ABC的各内角度数.
解:∵∠A+∠B+∠C=180°,
∠A=2∠B,∠C=∠B+20°,
∴2∠B+∠B+∠B+20°=180°,
∴∠B=40°,
∴∠A=2∠B=80°,∠C=∠B+20°=60°.
6.如图,在△ABC中,CE平分∠ACB,∠1=∠2,若∠ACE=23°,求∠EDC的度数.
第6题图
解:∵CE平分∠ACB,∠ACE=23°,
∴∠1=∠ACE=23°,
∵∠1=∠2,∴∠2=23°,
∵∠EDC+∠2+∠1=180°,
∴∠EDC=180°-(∠2+∠1)=134°.
7.如图,在△ABC中,∠A=50°,∠ABD=35°,∠ACB=70°,且CE平分∠ACB,求∠BEC的度数.
第7题图
解:∵∠A=50°,∠ACB=70°,
∴∠ABC=180°-∠A-∠ACB=60°,
∵∠ABD=35°,
∴∠CBD=∠ABC-∠ABD=25°,
∵CE平分∠ACB,
∴∠BCE=∠ACB=35°,
∴在△BCE中,∠BEC=180°-∠CBD-∠BCE=120°.
8.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,求∠C的度数.
第8题图
解:如图,
由题意得∠BAE=45°,∠CAE=15°,∠DBC=85°,
∵AE∥BD,∴∠DBA=∠BAE=45°,
∴∠ABC=∠DBC-∠DBA=40°,∠BAC=∠BAE+∠CAE=60°,
由三角形的内角和定理,得:
∠C=180°-∠BAC-∠ABC=80°.
一、填空题
9.设三角形的三个内角分别为α、β、γ,且α≥β≥γ,α=2γ,则β的最大值与最小值的和是 117° .
10.如图,在△ABC中,点D、E分别在边BC、AC上,∠DCE=∠DEC,点F在AC上,点G在DE的延长线上,连接GF,且∠DFG=∠DGF.若∠EFG=35°,则∠CDF的度数为 70° .
117°
70°
第10题图
二、解答题
11.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的点A'处,折痕为DE.已知∠BDA'=110°,∠C=70°,∠B=80°,设∠CFD=α,∠CEA'=β,求α和β的度数.
第11题图
解:∵∠C=70°,∠B=80°,
∴∠A=180°-∠B-∠C=30°,
∵∠BDA'=110°,
∴∠ADA'=180°-∠BDA'=70°,
∴∠AFD=180°-∠ADA'-∠A=80°,
∴α=180°-∠AFD=100°,
∴∠A'FE=α=100°,
由折叠可知,∠A'=∠A=30°,
∴β=180°-∠A'-∠A'FE=50°.
解答题
12.如图,BD、CE相交于点A,连接CB,DE.
(1)探索∠B、∠C、∠D、∠E之间的数量关系,并说明理由;
解:(1)∠B+∠C=∠D+∠E,理由如下:
∵∠B+∠C+∠BAC=180°,∠D+∠E+∠DAE=180°,∠BAC=∠DAE,
∴∠B+∠C=∠D+∠E;
第12题图
(2)若∠BCE、∠BDE的角平分线相交于点O,利用(1)中的结论探索∠B、∠E、∠O之间的数量关系,并说明理由.
解:(2)∠B+∠E=2∠O,理由如下:
如图,
第12题图
类似于(1)中的结论,有:
∠B+∠BCO=∠O+∠BDO,
而∠BCO=∠BCA,∠BDO=∠BDE,
∴∠O=∠B+(∠BCA-∠BDE),
∵∠B+∠BCA=∠E+∠BDE,
∴∠BCA-∠BDE=∠E-∠B,
∴∠O=∠B+(∠E-∠B),
∴∠B+∠E=2∠O.
谢 谢 观 看
第4课时 三角形的内角(2)
第十一章 三角形
一、选择题
1.在一个直角三角形中,有一个锐角为35°,则另一个锐角的度数是( C )
A.75° B.65° C.55° D.45°
2.如图,△ABC中,∠C=90°,则∠B=( D )
A.15° B.30° C.50° D.60°
第2题图
C
D
3.如图,已知在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( B )
A.90° B.20° C.45° D.70°
第3题图
B
第4题图
4.如图,在△ABC中,∠ACB=90°,过点C作CD∥AB交∠ABC的平分线于点D,若∠ABD=20°,则∠ACD的度数为( D )
D
A.20° B.30° C.40° D.50°
二、填空题
5.在Rt△ABC中,∠C=90°,∠A=70°,则∠B= 20° .
6.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为点E.若∠CAD=20°,则∠EDB的度数是 40° .
第6题图
20°
40°
三、解答题
7.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD的延长线于点E.若∠DBE=28°,求∠CAB的度数.
第7题图
解:∵BE⊥AE,
∴∠E=90°=∠C,
∵∠ADC=∠BDE,
∴∠CAD=∠DBE=28°,
∵AE平分∠CAB,
∴∠CAB=2∠CAD=56°.
8.如图,在Rt△ABC中,∠C=90°,∠CAB、∠CBA的角平分线AD、BE交于点F,求∠AFB的度数.
第8题图
解:∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵AD平分∠CAB,BE平分∠CBA,
∴∠FAB=∠CAB,∠FBA=∠CBA,
∴∠FAB+∠FBA=(∠CAB+∠CBA)=45°,
∴∠AFB=180°-(∠FAB+∠FBA)=135°.
9.如图,AB、ED分别垂直于BD,点B、D是垂足,且∠ACB=∠CED.求证:△ACE是直角三角形.
第9题图
证明:∵ED⊥BD,
∴∠CDE=90°,
∴∠CED+∠DCE=90°,
∵∠ACB=∠CED,
∴∠ACB+∠DCE=90°,
∴∠ACE=180°-(∠ACB+∠DCE)=90°,
∴△ACE是直角三角形.
一、选择题
10.如图,CD是Rt△ABC斜边AB上的高,且CB>CA,图中相等的角共有( D )
A.2对 B.3对 C.4对 D.5对
第10题图
D
11.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在边AC上的点E处,若∠A=25°,则∠ADE的度数为( A )
A.40° B.50° C.65° D.75°
第11题图
A
二、解答题
12.如图,在△ABC中,∠A=30°,∠B=60°,CE平分∠ACB,点F在CE上.
(1)求∠ACE的度数;
(1)解:∵∠A=30°,∠B=60°,
∴∠ACB=180°-∠A-∠B=90°,
又∵CE平分∠ACB,
∴∠ACE=∠ACB=45°;
第12题图
(2)若CD⊥AB于点D,∠CDF=75°,求证:△CFD是直角三角形.
(2)证明:∵CD⊥AB,∠B=60°,
∴∠BCD=90°-∠B=30°,
又∵∠BCE=∠ACE=45°,
∴∠DCF=∠BCE-∠BCD=15°,
又∵∠CDF=75°,
∴∠CFD=180°-∠CDF-∠DCF=90°,
∴△CFD是直角三角形.
第12题图
解答题
13.如图,已知在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数;
解:(1)∵∠B=70°,∠C=30°,
∴∠BAC=180°-∠B-∠C=80°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=40°;
第13题图
(2)求∠DAE的度数;
解:(2)∵AD⊥BC,∴∠ADE=∠ADB=90°,
∴∠B+∠BAD=90°,
∴∠BAD=90°-∠B=20°,
∴∠DAE=∠BAE-∠BAD=20°;
第13题图
解:(3)能.
∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠BAE=∠BAC=(180°-∠B-∠C)=90°-(∠B+∠C),
∵AD⊥BC,∴∠ADB=90°,
∴∠B+∠BAD=90°,∴∠BAD=90°-∠B,
∴∠DAE=∠BAE-∠BAD=90°-(∠B+∠C)-(90°-∠B)=(∠B-∠C),
第13题图
(3)探究:如果将条件“∠B=70°,∠C=30°”改成“∠B-∠C=40°”,能否得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
∵∠B-∠C=40°,
∴∠DAE=×40°=20°.
谢 谢 观 看
第5课时 三角形的外角
第十一章 三角形
一、选择题
1.如图,已知∠ACD=130°,∠B=20°,则∠A的度数是( A )
A.110° B.130° C.150° D.90°
第1题图
2.将一副直角三角板按如图所示的方式叠放,则∠1的度数为( A )
A.105° B.100° C.95° D.110°
第2题图
A
A
3.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( D )
A.75° B.105° C.135° D.165°
第3题图
D
4.如图,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,若∠ABP=20°,∠ACP=50°,则∠A=( A )
A.60° B.80° C.70° D.50°
第4题图
A
二、填空题
5.△ABC中,∠B=65°,∠A比∠C小35°,则与∠C相邻的外角的度数为 105° .
6.如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2= 101° .
第6题图
105°
101°
三、解答题
7.如图,已知D为BC上一点,∠B=∠1,∠BAC=64°,求∠2的度数.
第7题图
解:∵∠BAC=64°,
∴∠BAD+∠1=64°,
∵∠B=∠1,
∴∠B+∠BAD=64°,
∵∠2是△ABD的外角,
∴∠2=∠B+∠BAD=64°.
8.如图,若∠A=27°,∠B=45°,∠C=38°,求∠DFE的度数.
第8题图
解:∵∠A=27°,∠C=38°,
∴∠AEB=∠A+∠C=65°,
∵∠B=45°,
∴∠DFE=∠B+∠BEF=110°.
9.如图,在△ABC中,∠1=100°,∠C=80°,∠2=∠3,BE平分∠ABC,求∠4的度数.
第9题图
解:∵∠1=100°,∠C=80°,
∴∠3=∠1-∠C=20°,
∵∠2=∠3,∴∠2=10°,
∴∠ABC=180°-∠1-∠2=70°,
∵BE平分∠ABC,∴∠ABE=∠ABC=35°,
∵∠4=∠2+∠ABE,
∴∠4=45°.
一、填空题
10.如图,∠CAD和∠CBD的平分线相交于点P.设∠CAD、∠CBD、∠C、∠D的度数依次为a、b、c、d,用仅含其中2个字母的代数式来表示∠P的度数为 .
第10题图
二、解答题
11.如图,点D、E分别在AC、AB上,BD、CE交于点F,∠B∶∠C=3∶2.
(1)若∠A=60°,∠DFE=100°,求∠BEC的度数;
解:(1)设∠B=3x,则∠C=2x,
∵∠DFE=∠FDC+∠C,∠FDC=∠A+∠B,
∴∠DFE=∠C+∠A+∠B,
即3x+2x+60°=100°,解得x=8°,
∴∠B=24°,∠C=16°,
∴∠BEC=∠A+∠C=76°;
第11题图
(2)若∠DFE-∠A=130°,求∠B的度数.
解:(2)∵∠DFE=∠C+∠A+∠B,
∴∠DFE-∠A=∠C+∠B,
∴3x+2x=130°,解得x=26°,
∴∠B=78°.
第11题图
解答题
12.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠P= ;
122°
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E,其中∠A=α,求∠E的度数;(用含α的代数式表示)
解:(2)如图,∵CE平分∠ACB,BE平分∠ABD,
∴∠1=∠ACB,∠2=∠ABD,
又∵∠ABD=∠A+∠ACB,
∴∠2=∠A+∠1,
∴∠E=∠2-∠1=∠A+∠1-∠1=;
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠Q与∠A的数量关系,并证明.
解:(3)∠Q=90°-∠A,
证明:∵BQ平分∠CBM,CQ平分∠BCN,
∴∠QBC=(∠A+∠ACB),∠QCB=(∠A+∠ABC),
∴∠Q=180°-∠QBC-∠QCB
=180°-(∠A+∠ACB)-(∠A+∠ABC)
=180°-∠A-(∠A+∠ABC+∠ACB)
=180°-∠A-90°
=90°-∠A.
谢 谢 观 看
第6课时 专题与角平分线有关的三角形内角和问题
第十一章 三角形
一、选择题
1.如图,点O是△ABC内一点,∠A= 80°,BO、CO分别是∠ABC、∠ACB的角平分线,则∠BOC的度数为( C )
A.140° B.135° C.130° D.125°
第1题图
C
2.如图,BP、CP分别为∠ABC、∠ACE的角平分线,若∠A= 45°,则∠P的度数是( B )
A.20° B.22.5° C.25° D.30°
第2题图
B
二、填空题
3.如图,在△ABC中,点O是∠ABC和∠ACB的平分线的交点,点E,D分别是OB,OC延长线上的点,∠CBE和∠BCD的平分线交于点P,∠A=α,则∠P的度数为 45°-α .(用含α的代数式表示)
第3题图
45°-α
三、解答题
4.如图,已知△OAB中,∠O=70°,∠OAB的平分线与△OBA的外角∠ABN的平分线所在的直线交于点D,求∠ADB的度数.
第4题图
解:∵AD平分∠OAB,
BC平分∠ABN,
∴∠ABC=∠ABN,
∠BAD=∠OAB,
∴∠ADB=∠ABC-∠BAD=(∠ABN-∠OAB)=∠O=35°.
5.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数.
第5题图
解:∵AD是BC上的高,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°-∠C=20°,
∵∠BAC=50°,AE平分∠BAC,
∴∠ABC=180°-∠BAC-∠C=60°,∠BAO=∠BAC=25°,
∵BF平分∠ABC,∴∠ABO=∠ABC=30°,
∴∠AOB=180°-∠ABO-∠BAO=125°.
6.如图所示,在△ABC中,∠A=40°,BP、CP是△ABC的外角平分线,求∠P的度数.
第6题图
解:∵BP、CP是△ABC的外角平分线,
∴∠PBC+∠PCB=(∠A+∠ACB+∠A+∠ABC)=110°,
∴∠P=180°-(∠PBC+∠PCB)=70°.
一、选择题
7.如图,△ABC中,∠ABD=∠DBE=∠EBC,∠ACD=∠DCE=∠ECB,若∠BEC=145°,则∠BDC的度数为( D )
A.80° B.90° C.100° D.110°
第7题图
D
二、填空题
8.如图,AB∥CD,∠1=∠2,BC交AD于点E.
(1)如图1,若AD⊥BD于点D,∠DAB=40°,则∠3的度数为 25 °;
25
(2)如图2,∠BAD与∠BDF的平分线交于点P,若∠ADB=70°,则∠P的度数为 55 °.
55
三、解答题
9.在△ABC中,若存在一个内角角度是另外一个内角角度的n倍(n为大于1的正整数),则称△ABC为n倍角三角形.例如,在△ABC中,∠A=80°,∠B=75°,∠C=25°,可知∠B=3∠C,故△ABC为3倍角三角形.
(1)在△ABC中,∠A=80°,∠B=60°,则△ABC为 倍角三角形;
2
(2)若锐角△MNP是3倍角三角形,且最小内角为α,则α的范围为 ;
22.5°<α<30°
(3)如图,直线MN与直线PQ垂直相交于点O,点A在射线OP上运动(点A不与点O重合),点B在射线OM上运动(点B不与点O重合).延长BA至点G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于点E、F,若△AEF为4倍角三角形,求∠ABO的度数.
第9(3)题图
解:(3)∵AE平分∠BAO,AF平分∠OAG,
∴∠EAB=∠EAO,∠OAF=∠FAG,
∴∠EAF=∠EAO+∠OAF=(∠BAO+∠OAG)=90°,
∵△EAF是4倍角三角形,∠F>∠E,
∴∠E=×90°或×90°,即∠E=22.5°或18°,
∵OE平分∠BOQ,∴∠E=∠ABO,
∴∠ABO=2∠E=45°或36°.
解答题
10.如图1,直线m与直线n相交于点O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO、∠ABO的角平分线.
(1)若∠BAO=50°,∠ABO=40°,求∠ACB的度数;
解:(1)∵AC、BC分别是∠BAO、∠ABO的角平分线,
∴∠CAB=∠BAO=25°,∠CBA=∠ABO=20°,
∴∠ACB=180°-∠CAB-∠CBA=135°;
(2)如图2,若∠AOB=α,BD是△AOB的外角∠OBE的角平分线,BD与AC延长线交于点D,点A、B在运动的过程中,∠ADB的度数是否发生变化?若发生变化,请说明理由;若不发生变化,试求出其度数(用含α的代数式表示);
解:(2)∠ADB的度数不发生变化,
∵AC平分∠BAO,BD平分∠OBE,
∴∠BAD=∠BAO,∠EBD=∠OBE,
∴∠ADB=∠EBD-∠BAD=(∠OBE-∠BAO)=∠AOB=α;
(3)如图3,若直线m与直线n相互垂直,延长AB至E,已知∠OBE、∠ABO的角平分线与∠BOQ的角平分线及其延长线分别相交于点D、F,在△BDF中,如果有一个角是另一个角的3倍,请直接写出∠BAO的度数.
解:(3)∠BAO=60°或45°.
谢 谢 观 看
第7课时 多边形
第十一章 三角形
一、选择题
1.下列图形中是多边形的是( D )
A
B
C
D
2.下列图形中∠1是外角的是( D )
A
B
C
D
D
D
3.下列说法正确的是( B )
A.一个多边形外角的个数与边数相同
B.一个多边形外角的个数是边数的二倍
C.每个角都相等的多边形是正多边形
D.每条边都相等的多边形是正多边形
4.如图所示的图形中,矩形的个数是( D )
A.3个 B.4个 C.5个 D.6个
第4题图
B
D
5.长方形剪去一个角后所得的图形一定不是( C )
A.五边形 B.梯形 C.长方形 D.三角形
C
二、填空题
6.如图所示,将多边形分割成三角形,①中可分割出2个三角形,②中可分割出3个三角形,③中可分割出4个三角形,…,由此能猜测出n边形可以分割出 (n-1) 个三角形.
第6题图
(n-1)
第7题图
7.如图,把边长为12的正三角形纸板剪去三个小正三角形,得到正六边形,则剪去的小正三角形的边长为 4 .
4
三、解答题
8.画出下列多边形的全部对角线.
第8题图
解:如图所示:
9.一个四边形的周长是46cm,已知第一条边的边长是acm,第二条边的边长比第一条边的边长的三倍少5cm,第三条边的边长等于第一、第二条边的边长之和.
(1)请用含a的式子表示第四条边的边长;
解:(1)由题意得:第二条边的边长为(3a-5)cm,第三条边的边长为a+3a-5=(4a-5)cm,
则第四条边的边长为46-a-(3a-5)-(4a-5)=(56-8a)cm,
答:第四条边的边长为(56-8a)cm;
(2)当a=7时还能得到四边形吗?为什么?此时的图形是什么形状?
解:(2)当a=7时不能得到四边形,理由如下:
∵此时第四条边的边长为56-8a=0cm,只剩下三条边,
∴三条边的边长分别为a=7cm,3a-5=16cm,4a-5=23cm,
∵7+16=23cm,∴图形是线段,
答:当a=7时不能得到四边形,此时的图形是线段.
一、选择题
10.若一个多边形截去一个角后,变成十五边形,则原来的多边形的边数为( A )
A.14或15或16 B.15或16
C.14或16 D.15或16或17
A
二、填空题
11.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形共有k条对角线,则(m-k)n的值是 125 .
125
三、解答题
12.已知正n边形的周长为60,边长为a.
(1)当n=3时,请直接写出a的值;
解:(1)a=60÷3=20;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n=3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若对,请给出证明;若不对,请求出不符合这一说法的n的值.
解:(2)这种说法不对.
令a=b,得=,
∴60n+420=67n,
解得n=60,
∴当n=60时,a=b,
即不符合这一说法的n的值为60.
解答题
13.阅读材料:
我们知道计算n边形的对角线条数公式为,如果有一个n边形的对角线一共有20条,那么可以得到方程=20,去分母得n(n-3)=40,由于n为大于等于3的整数,且n比n-3的值大3,所以满足积为40且相差3的因数只有8和5,符合方程的整数解为n=8,即多边形是八边形.根据材料内容,回答下列问题:
(1)若有一个多边形的对角线一共有14条,求这个多边形的边数;
解:(1)由题意得,=14,
去分母得:n(n-3)=28,
∵n为大于等于3的整数,且n比n-3的值大3,
∴满足积为28且相差3的因数只有7和4,
符合方程的整数解为n=7,
即这个多边形的边数为7;
(2)A同学说:“我求得一个多边形的对角线一共有30条.”你认为A同学的说法正确吗?为什么?
解:(2)A同学的说法不正确,理由如下:
∵=30,去分母得n(n-3)=60,
当n=9时,n(n-3)=9×6=54<60,
当n=10时,n(n-3)=10×7=70>60,
∴符合方程的正整数n不存在,即多边形的对角线不可能有30条,
∴A同学的说法不正确.
谢 谢 观 看
第8课时 多边形的内角和
第十一章 三角形
一、选择题
1.内角和为540°的多边形是( C )
A.三角形 B.四边形 C.五边形 D.六边形
2.已知一个正多边形的一个内角为150度,则它的边数为( A )
A.12 B.9 C.8 D.7
3.一个正多边形,它的一个内角恰好是一个外角的4倍,则这个正多边形的边数是( C )
A.8 B.9 C.10 D.12
C
A
C
4.如图,在一个三角形纸片ABC中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED,则图中∠1+∠2的度数为( C )
A.90° B.180° C.270° D.315°
第4题图
C
二、填空题
5.九边形的内角和为 1260° ,从一个顶点出发有 6 条对角线,共有 27 条对角线.
6.如图,已知∠1+∠2+∠3=310°,则∠4= 50° .
第6题图
1260°
6
27
50°
三、解答题
7.已知一个多边形的内角和与外角和之比是3∶2,求这个多边形的边数.
解:设这个多边形的边数为n,
依题意得:(n-2)×180°=×360°,
解得n=5,
∴这个多边形的边数为5.
8.如图,若正五边形ABCDE和长方形AFCG按如图方式叠放在一起,求∠EAF的度数.
第8题图
解:∵正五边形内角和为540°,
∴其每个内角为540°÷5=108°,
∵长方形每个内角为90°,∴∠F=90°,
∴∠ABC=108°,∠ABF=180°-∠ABC=72°,
∴∠BAF=180°-∠F-∠ABF=18°,
∴∠EAF=∠EAB+∠BAF=126°.
9.如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(1)解:∵六边形ABCDEF的各内角相等,
∴一个内角的度数为=120°,
∴∠E=∠F=∠FAB=120°,
∵∠1=48°,
∴∠FAD=∠FAB-∠1=72°,
∵∠2+∠FAD+∠F+∠E=360°,
∴∠2=360°-∠FAD-∠F-∠E=48°;
第9题图
(2)求证:AB∥DE.
(2)证明:由(1)知∠E=∠F=∠FAB=120°,
∴∠1=∠FAB-∠DAF=120°-∠DAF,
∠2=360°-∠E-∠F-∠DAF=120°-∠DAF,
∴∠1=∠2,∴AB∥DE.
第9题图
一、选择题
10.如图,在正五边形ABCDE中,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G=( B )
A.36° B.54° C.60° D.72°
第10题图
B
二、填空题
11.已知一个多边形,少算一个内角的度数,其余内角和为2100°,则这个多边形的边数为 14 .
14
三、解答题
12.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
第12题图
解:如图,连接CG,
∵∠COG=∠AOB,
∴∠6+∠7=∠OCG+∠OGC,
又∵在五边形CDEFG中,
∠1+∠2+∠OCG+∠OGC+∠3+∠4+∠5=(5-2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
解答题
13.(1)如图1,在△ABC中,BD平分∠ABC,且与△ABC的外角∠ACE的平分线交于点D,若∠ABC=75°,∠ACB=45°,求∠D的度数;
解:(1)∵BD平分∠ABC,CD平分∠ACE,
∴∠DBC=∠ABC,∠DCE=∠ACE,
∵∠ACE=∠ABC+∠A,
∠DCE=∠DBC+∠D,
∴∠DCE=∠ACE=(∠ABC+∠A),
即∠DBC+∠D=(∠ABC+∠A),
∴∠D=∠A,
∵∠ABC=75°,∠ACB=45°,
∴∠A=180°-∠ABC-∠ACB=60°,
∴∠D=∠A=30°;
(2)如图2,在四边形MNCB中,BD平分∠MBC,且与四边形MNCB的外角∠NCE的平分线交于点D,若∠BMN=130°,∠CNM=100°,求∠D的度数.
解:(2)如图,延长BM,CN交于点A,
∵∠BMN=∠ANM+∠A,
∠CNM=∠AMN+∠A=180°-∠ANM,
∴∠A=∠BMN+∠CNM-180°=50°,
由(1)知∠D=∠A,
∴∠D=25°.
谢 谢 观 看
第9课时 复习巩固
第十一章 三角形
一、选择题
1.以下列长度的各组线段为边,能组成三角形的是( D )
A.2cm,3cm,5cm B.3cm,3cm,6cm
C.5cm,8cm,2cm D.4cm,5cm,6cm
2.已知正多边形的一个内角是135°,则这个正多边形的边数是( D )
A.3 B.4 C.6 D.8
D
D
3.如图,AM是△ABC的中线,△ABC的面积为4cm2,则△ABM的面积为( C )
A.8cm2 B.4cm2
C.2cm2 D.以上答案都不对
第3题图
C
二、填空题
4.如图,在△ABC中,AD是角平分线,AE是中线,AF是高.如果BC=10cm,那么BE= 5cm ;如果∠ABC=40°,∠ACB=60°,那么∠BAD= 40° ,∠DAF= 10° .
第4题图
5.三角形三个内角度数之比是1∶1∶2,则这个三角形是 等腰直角 三角形.
5cm
40°
10°
等腰直角
6.若从一个多边形的一个顶点出发可以引5条对角线,则这个多边形的内角和为 1080° .
7.如图,五边形ABCDE的每一个内角都相等,则外角∠CBF= 72° .
第7题图
1080°
72°
三、解答题
8.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是△ABC内部的一条线段,AE交CD于点F,交CB于点E,且∠CFE=∠CEF.求证:AE平分∠CAB.
第8题图
证明:∵CD⊥AB,
∴在Rt△ADF中,
∠DAF=90°-∠AFD=90°-∠CFE,
∵∠ACE=90°,
∴在Rt△AEC中,∠CAE=90°-∠CEF,
∵∠CFE=∠CEF,
∴∠DAF=∠CAE,
即AE平分∠CAB.
9.如图,在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40的两部分,求AC和AB的长.
第9题图
解:∵AD是BC边上的中线,
∴BD=CD,
∵AC>AB,
∴AC+CD=60,AB+BD=40,
设BD=CD=x,AB=y,则AC=2BC=4x,
∴4x+x=60,x+y=40,
解得:x=12,y=28,
∴AC=4x=48,AB=28.
一、填空题
10.如图,△ABC的三条中线AD,BE,CF交于点G,若S△ABC=12,则图中阴影部分的面积是 4 .
第10题图
4
二、解答题
11.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获.如图所示的两幅图都是由同一副直角三角板拼凑得到的.
(1)如图1,求∠ABC的度数;
解:(1)∵∠F=30°,∠EAC=45°,
∴∠ABF=∠EAC-∠F=15°,
∵∠FBC=90°,
∴∠ABC=∠FBC-∠ABF=75°;
(2)如图2,若AE∥BC,求∠AFD的度数.
解:(2)∵∠B=60°,∠BAC=90°,∴∠C=30°,
∵AE∥BC,∴∠CAE=∠C=30°,
∴∠AFD=∠CAE+∠E=75°.
解答题
12.如图1,点D为△ABC内一点,连接BD,CD.
第12题图1
(1)探究∠BDC与∠A,∠ABD,∠ACD之间的关系,并说明理由;
解:(1)∠BDC=∠A+∠ABD+∠ACD,
理由:如图,连接AD并延长交BC于点E,
∵∠BDE=∠BAE+∠ABD,
∠EDC=∠EAC+∠ACD,
∴∠BDE+∠EDC=∠BAE+∠EAC+∠ABD+∠ACD,
∴∠BDC=∠BAC+∠ABD+∠ACD;
(2)请直接用(1)中的结论,解决下列问题:
①当∠BDC=120°时,若∠A=50°,则∠ABD+∠ACD= °;
②如图2,BE平分∠ABD,CE平分∠ACD,若∠BDC=120°,∠A=50°,求∠BEC的度数;
③如图3,∠ABD,∠ACD的n等分线相交于点E1,E2,…,En-1,若∠BDC=x°,∠BE1C=y°,求∠A的度数.(用含x,y,n的式子表示)
70
解:(2)②∵BE平分∠ABD,CE平分∠ACD,
∴∠ABE=∠ABD,∠ACE=∠ACD,
∴∠BEC=∠ABE+∠ACE+∠A=(∠ABD+∠ACD)+∠A
=×(∠BDC-∠A)+50°=85°;
③以此类推(∠BDC-∠A)+∠A=∠BE1C,
即(x°-∠A)+∠A=y°,
则∠A=.
谢 谢 观 看
