6.1.1 函数的平均变化率 教学设计
文档属性
| 名称 | 6.1.1 函数的平均变化率 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 624.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-24 00:00:00 | ||
图片预览

文档简介
教学设计
教学目标
(1)能够通过具体情境直观理解导数概念,感悟极限思想,知道极限思想是人类深刻认识和表达现实世界必备的思维品质,理解导数是一种建立在极限上的运算。理解其几何意义。
(2)掌握导数的基本运算规则,能求简单导数和简单复合函数的导数。
(3)重点提升数学抽象,数学运算,直观想象,数学建模和逻辑推理素养。
重难点
(1)通过对跑步运动过程中平均速率与瞬时速度之间的关系,体会极限思想理解导数是一种建立在极限上,提升其数学建模、逻辑推理素养。
(2)通过对函数平均变化率和瞬时转化率之间的关系,体会瞬时变化率即为函数的导数;同时由曲线割线的斜率去逼近切线的斜率,理解导数的几何意义,体会数与形的有机结合,提升学生的直观想象、逻辑推理等素养。
(3)能够计算简单导数和简单复合函数的导数,提升学生对导数概念的理解,提升学生的数学运算素养。
教学过程
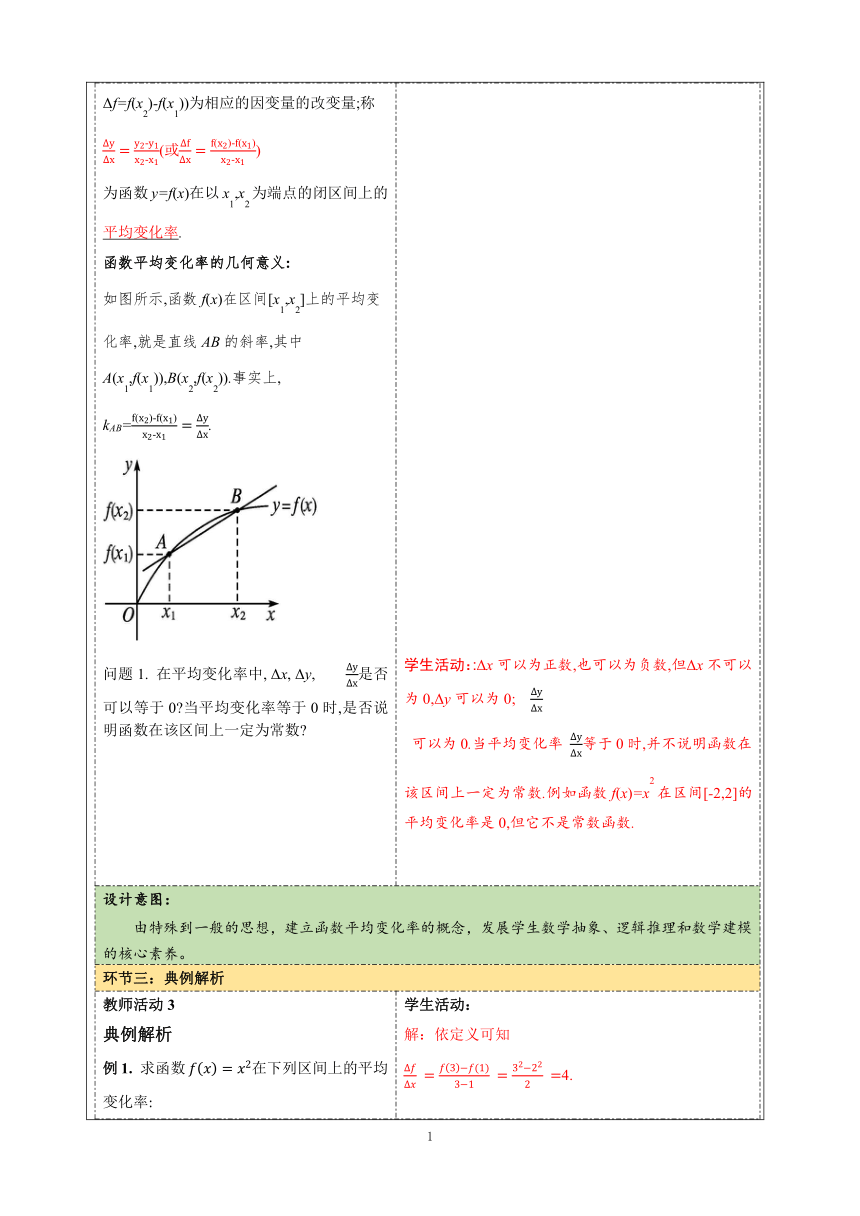
教师活动学生活动环节一:情景导学 【展示】运动员的比赛视频,计算得到其平均速度。 【提问】如何得到运动员在2s时的瞬时速度学生活动1 【回答】思考后探索由平均速度去逼近瞬时速度 设计意图: 通过具体问题的思考和分析,提出计算平均变化率的问题。发展学生数学抽象和数学建模的核心素养。环节二:讲授新课函数的平均变化率 教师活动2 一般地,若函数y=f(x)的定义域为D,且x1,x2∈D,x1≠x2,y1=f(x1),y2=f(x2),则称Δx=x2-x1为自变量的改变量;称Δy=y2-y1(或Δf=f(x2)-f(x1))为相应的因变量的改变量;称 (或) 为函数y=f(x)在以x1,x2为端点的闭区间上的平均变化率. 函数平均变化率的几何意义: 如图所示,函数f(x)在区间[x1,x2]上的平均变化率,就是直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)).事实上, kAB=. 问题1. 在平均变化率中, Δx, Δy, 是否可以等于0 当平均变化率等于0时,是否说明函数在该区间上一定为常数 学生活动2 学生思考并讨论:对于定义,有哪几点值得注意? 学生活动::Δx可以为正数,也可以为负数,但Δx不可以为0,Δy可以为0; 可以为0.当平均变化率 等于0时,并不说明函数在该区间上一定为常数.例如函数f(x)=x2在区间[-2,2]的平均变化率是0,但它不是常数函数. 设计意图: 由特殊到一般的思想,建立函数平均变化率的概念,发展学生数学抽象、逻辑推理和数学建模的核心素养。环节三:典例解析教师活动3 典例解析 例1. 求函数在下列区间上的平均变化率:
(1) (2)以1和为端点的闭区间. 例1(2)的计算结果说明,函数在以1和为端点的闭区间上的平均变化率与有关; 增大时,平均变化率增大. 从几何上来看就是,当增大时,函数的图像上,连接(1,)与(1+ ,)的直线斜率将不断增大,如图所示的图中,直线AB的斜率小于直线AO的斜率,且直线,AO的斜率小于直线AC的斜率. 前述情境中的数据可以用图表示,若将作为时间的函数,除了根据已知数据得到的点以外,函数图像上其他点我们是不知道的.例如,函数图像有可能是图中黄色曲线,也有可能是绿色曲线
探究2.观察前述情景中的数据与图思考,怎样才能估计出时的值? 我们可以将图中的线段AB近似的看成在上的图像,从而由AB的方程可以计算出时的估计值: 因为直线AB的斜率为6.95,且B(5,8.8),所以有直线的点斜式可知AB的直线方程为 代入,可以算得,也就是说的估计值为.上述求估计值的关键是用直线段代替了曲线段,这在数学中简称为“以直代曲”. 二、平均速度与平均变化率 从物理学中我们知道,平均速度可以描述物体在一段时间内运动的快慢,如果物体运动的位移x m与时间t s的关系为x=h(t),则物体在[t1,t2](t1 即在上的平均变化率为4. (2)依定义可知 .
在以1和为端点的闭区间上的平均变化率为. 解:(1)所求平均速度为 (2)将 成直线,则由(1)可知, 直线的斜率为5,且直线通过点, 因此, 与的关系可近似地表示为 在上式中令,可求得,即物体的位移可以估计为 设计意图: 通过典型例题,加深学生对函数平均变化率的理解和运用,发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
1
教学目标
(1)能够通过具体情境直观理解导数概念,感悟极限思想,知道极限思想是人类深刻认识和表达现实世界必备的思维品质,理解导数是一种建立在极限上的运算。理解其几何意义。
(2)掌握导数的基本运算规则,能求简单导数和简单复合函数的导数。
(3)重点提升数学抽象,数学运算,直观想象,数学建模和逻辑推理素养。
重难点
(1)通过对跑步运动过程中平均速率与瞬时速度之间的关系,体会极限思想理解导数是一种建立在极限上,提升其数学建模、逻辑推理素养。
(2)通过对函数平均变化率和瞬时转化率之间的关系,体会瞬时变化率即为函数的导数;同时由曲线割线的斜率去逼近切线的斜率,理解导数的几何意义,体会数与形的有机结合,提升学生的直观想象、逻辑推理等素养。
(3)能够计算简单导数和简单复合函数的导数,提升学生对导数概念的理解,提升学生的数学运算素养。
教学过程
教师活动学生活动环节一:情景导学 【展示】运动员的比赛视频,计算得到其平均速度。 【提问】如何得到运动员在2s时的瞬时速度学生活动1 【回答】思考后探索由平均速度去逼近瞬时速度 设计意图: 通过具体问题的思考和分析,提出计算平均变化率的问题。发展学生数学抽象和数学建模的核心素养。环节二:讲授新课函数的平均变化率 教师活动2 一般地,若函数y=f(x)的定义域为D,且x1,x2∈D,x1≠x2,y1=f(x1),y2=f(x2),则称Δx=x2-x1为自变量的改变量;称Δy=y2-y1(或Δf=f(x2)-f(x1))为相应的因变量的改变量;称 (或) 为函数y=f(x)在以x1,x2为端点的闭区间上的平均变化率. 函数平均变化率的几何意义: 如图所示,函数f(x)在区间[x1,x2]上的平均变化率,就是直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)).事实上, kAB=. 问题1. 在平均变化率中, Δx, Δy, 是否可以等于0 当平均变化率等于0时,是否说明函数在该区间上一定为常数 学生活动2 学生思考并讨论:对于定义,有哪几点值得注意? 学生活动::Δx可以为正数,也可以为负数,但Δx不可以为0,Δy可以为0; 可以为0.当平均变化率 等于0时,并不说明函数在该区间上一定为常数.例如函数f(x)=x2在区间[-2,2]的平均变化率是0,但它不是常数函数. 设计意图: 由特殊到一般的思想,建立函数平均变化率的概念,发展学生数学抽象、逻辑推理和数学建模的核心素养。环节三:典例解析教师活动3 典例解析 例1. 求函数在下列区间上的平均变化率:
(1) (2)以1和为端点的闭区间. 例1(2)的计算结果说明,函数在以1和为端点的闭区间上的平均变化率与有关; 增大时,平均变化率增大. 从几何上来看就是,当增大时,函数的图像上,连接(1,)与(1+ ,)的直线斜率将不断增大,如图所示的图中,直线AB的斜率小于直线AO的斜率,且直线,AO的斜率小于直线AC的斜率. 前述情境中的数据可以用图表示,若将作为时间的函数,除了根据已知数据得到的点以外,函数图像上其他点我们是不知道的.例如,函数图像有可能是图中黄色曲线,也有可能是绿色曲线
探究2.观察前述情景中的数据与图思考,怎样才能估计出时的值? 我们可以将图中的线段AB近似的看成在上的图像,从而由AB的方程可以计算出时的估计值: 因为直线AB的斜率为6.95,且B(5,8.8),所以有直线的点斜式可知AB的直线方程为 代入,可以算得,也就是说的估计值为.上述求估计值的关键是用直线段代替了曲线段,这在数学中简称为“以直代曲”. 二、平均速度与平均变化率 从物理学中我们知道,平均速度可以描述物体在一段时间内运动的快慢,如果物体运动的位移x m与时间t s的关系为x=h(t),则物体在[t1,t2](t1
在以1和为端点的闭区间上的平均变化率为. 解:(1)所求平均速度为 (2)将 成直线,则由(1)可知, 直线的斜率为5,且直线通过点, 因此, 与的关系可近似地表示为 在上式中令,可求得,即物体的位移可以估计为 设计意图: 通过典型例题,加深学生对函数平均变化率的理解和运用,发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
1
