第21章 二次根式 习题课件(共184张PPT) 2024-2025学年数学华东师大版九年级上册
文档属性
| 名称 | 第21章 二次根式 习题课件(共184张PPT) 2024-2025学年数学华东师大版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-26 00:00:00 | ||
图片预览





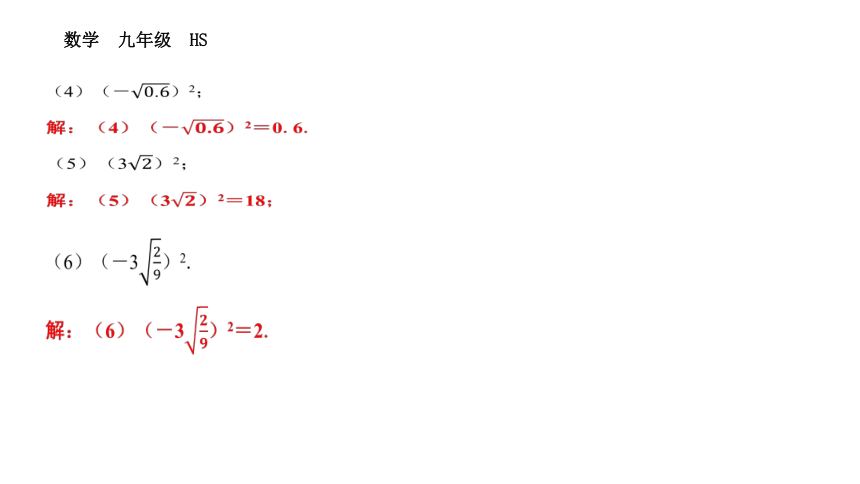






文档简介
(共184张PPT)
第1课时 二次根式(1)
第21章 二次根式
一、选择题
1.下列各式中,一定是二次根式的有( B )
①;②;③;④;⑤.
A.2个 B.3个 C.4个 D.5个
2.在下列各式中,一定是二次根式的是( D )
A. B.
C. D.
B
D
4.二次根式中,x的取值范围是( D )
A.x≥1 B.x≤1 C.x>1 D.x<1
D
3.若二次根式有意义,则( C )
A.x≠2 B.x>2 C.x≤2 D.x≥2
C
二、填空题
5.(1)使二次根式有意义的x的取值范围是 x≤2 ;
(2)当x ≥-1且x≠2 时,在实数范围内有意义.
x≤2
≥-1且x≠2
三、解答题
6.计算:
(1)()2;
解:(1)()2=4;
(2)()2;
解:(2)()2=.
(3)()2;
解:(3)()2=0;
(4)(-)2;
解:(4)(-)2=0.6.
(5)(3)2;
解:(5)(3)2=18;
(6)(-3)2.
解:(6)(-3)2=2.
7.当x取何值时,下列各式在实数范围内有意义?
(1)+;
解:要使有意义,则3-x≥0,即x≤3,
要使有意义,则x-2≥0,即x≥2,
∴当2≤x≤3时,+有意义.
(2);
解:∵1-=1-|x|,
∴当x=±1时,1-|x|=0,原式没有意义,
∴当x≠±1时,有意义.
(3)+;
解:要使有意义,则2x≥0,即x≥0,
要使有意义,则-2x≥0,即x≤0,
∴当x=0时,+有意义.
(4).
解:要使有意义,则x+2≥0且3x≠0,
即x≥-2且x≠0,
∴当x≥-2且x≠0时,有意义.
8.已知y=++4,求的值.
解:根据题意得,解得x=3,
将x=3代入y=++4,得y=4,
∴x2+y2=25,∴=5.
一、填空题
9.使代数式+有意义的整数x的和是 -6 .
-6
二、解答题
10.(1)若a、b为实数,且b=,求-的值;
解:由题意得,a2-1≥0,1-a2≥0,
∴a2=1,即a=±1,
∵a+1≠0,∴a≠-1,
∴a=1,
∴b==,
∴-=-=-3.
(2)已知|x-1000|+()2=2000,y=++,求y-x的平方根;
解:由题意得,998-x≥0,m-1≥0,1-m≥0,m+8≥0,
解得x≤998,m=1,
∴1000-x+998-x=2000,
解得x=-1,
∴y=++=3,
∴y-x=3-(-1)=4,
∴y-x的平方根是±2.
(3)与|3-a-|是相反数,求+的值.
解:由题意得+|3-a-|=0,
∴3-a-=0,解得a+=3,
∴a+2+=5,
∴(+)2=5,
∴+=.
解答题
11.观察下列各式:
=1+=1+;
=1+=1+;
=1+=1+;
…,
请利用你发现的规律,计算:
+++…+.
解:原式=1++1++1++…+1+
=2023+-+…+
=2023+1-
=2023.
谢 谢 观 看
第2课时 二次根式(2)
第21章 二次根式
一、选择题
1.下列式子是二次根式的是( C )
A. B.
C. D.
2.二次根式的值为( D )
A.-2 B.±2 C.4 D.2
C
D
4.在下列各式中,正确的是( C )
A.=±4 B.=-4
C.-=-4 D.=a
C
3.已知=a-1,那么a的取值范围为( B )
A.a>1 B.a≥1 C.a<1 D.a≤1
B
二、填空题
5.(1)化简:= -2 ;
(2)已知a<0,b>0,化简:= b-a .
6.若=3-b,则b应满足 b≤3 .
-2
b-a
b≤3
三、解答题
7.化简:
(1);
解:(1)=0.3;
(2);
解:(2)==0.6.
(3);
解:(3)=|-|=;
(4)-;
解:(4)-=-|-π|=-π.
(5)+|3-x|(x<2).
解:(5)原式=+|3-x|
=2-x+3-x
=5-2x.
8.(1)计算:+;
解:原式=+
=π-3+5-π
=2.
(2)化简:+(2≤x≤3).
解:∵2≤x≤3,
∴x-2≥0,x-3≤0,
∴原式=+
=+
=x-2+3-x
=1.
9.实数a,b在数轴上的位置如图所示,化简:+|a+b|+.
第9题图
解:由数轴可知,-2<a<-1,2<b<3,
∴a+1<0,a+b>0,b-3<0,
原式=+(a+b)+|b-3|
=-(a+1)+(a+b)+(3-b)
=2.
一、选择题
10.(1)计算()2+的结果是( C )
A.-1 B.2x-5 C.5-2x D.1
(2)若式子+的值为2,则a的取值范围是( D )
A.a≤4 B.a≥2
C.a=2或4 D.2≤a≤4
C
D
二、解答题
11.(1)a、b、c都是实数,且|a|+a=0,=1,|c|-c=0.试求-|a+b|-+|c-a|的值;
解:由题意得a<0,b<0,c≥0,
∴-|a+b|-+|c-a|
=-b+(a+b)-(c-b)+(c-a)
=b.
(2)若实数x,y,m满足关系式+=·,求m的值.
解:依题意,得,解得x+y=20,
∴+=0,
∴3x+3y-m=0,
∴m=3(x+y)=60,
即m的值是60.
解答题
12.阅读下列材料,回答问题:
在化简的过程中,小张和小李的化简结果不同.
小张的化简如下:
=
==-;
小李的化简如下:
=
==-.
(1)请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由;
解:(1)小李的化简结果正确,小张的化简结果错误.理由如下:
∵<,∴-<0,
∴=|-|=-(-)=-;
(2)请你利用上面正确的方法化简:
①;②.
解:(2)①原式===+1;
②原式===-1.
谢 谢 观 看
第3课时 二次根式的乘法
第21章 二次根式
一、选择题
1.如果·=成立,那么a满足的条件是( C )
A.a≥-2 B.-2≤a≤3
C.a≥3 D.a为一切实数
2.在下列各数中,与的积仍为无理数的是( D )
A. B. C. D.
C
D
3.下列运算:①2×3=6;②4·=4;③2·3=3;④×=,其中正确的有( B )
A.0个 B.1个 C.2个 D.3个
B
二、填空题
4.如果等式·=成立,那么有x+1 ≥ 0,1-x ≥ 0,所以x的取值范围是 -1≤x≤1 .
5.计算:
≥
≥
-1≤x≤1
(1)2×= 2 ;
(2)×= 3 ;
(3)×= 3 ;
(4)2×= 2 ;
(5)×3= 6 .
2
3
3
2
6
6.矩形的长和宽分别为和,则这个矩形的面积为 .
7.如果·=0,那么a= 6 .
6
三、解答题
8.计算:
(1)×;
解:原式==.
(2)×;
解:原式==10.
(3)×;
解:原式==9.
(4)×;
解:原式==1.2.
(5)×;
解:原式==.
(6)4×(-3);
解:原式=-12×=-48.
(7)××;
解:原式=×=2.
(8)2×3×;
解:原式=(2×3)
=6×
=120.
(9)××.
解:原式===3.
一、选择题
9.计算·的结果为( D )
A. B. C.13 D.1
D
二、解答题
10.已知一个长方体的长、宽、高分别为3cm、2cm、2cm.求这个长方体的体积.
解:∵长方体的长、宽、高分别为3cm、2cm、2cm,
∴3×2×2=3×2×2=72cm3,
答:这个长方体的体积为72cm3.
解答题
11.阅读下列解题过程:
例:若代数式+的值是2,求a的取值范围.
解:原式=|a-1|+|a-3|,
当a<1时,原式=(1-a)+(3-a)=4-2a=2,解得a=1(舍去);
当1≤a≤3时,原式=(a-1)+(3-a)=2=2,符合条件;
当a>3时,原式=(a-1)+(a-3)=2a-4=2,解得a=3(舍去),
综上所述,a的取值范围是1≤a≤3.
上述解题过程主要运用了分类讨论的方法,请你根据上述方法,解答下列问题:
(1)当2≤a≤5时,化简:+;
解:(1)∵2≤a≤5,
∴a-2≥0,a-5≤0,
∴原式=|a-2|+|a-5|
=a-2-(a-5)
=3;
(2)若等式+=4成立,求a的取值范围;
解:(2)由题意可知:|3-a|+|a-7|=4,
当a<3时,3-a>0,a-7<0,
∴原方程化为3-a-(a-7)=4,
∴a=3(舍去);
当3≤a≤7时,3-a≤0,a-7≤0,
∴原方程化为-(3-a)-(a-7)=4,
∴4=4,故3≤a≤7符合题意;
当a>7时,3-a<0,a-7>0,
∴原方程化为-(3-a)+(a-7)=4,
∴a=7(舍去),
综上所述,a的取值范围是3≤a≤7;
(3)若+=8,求a的值.
解:(3)原方程可化为|a+1|+|a-5|=8,
当a<-1时,a+1<0,a-5<0,
∴原方程化为-(a+1)-(a-5)=8,
∴a=-2,符合题意;
当-1≤a≤5时,a+1≥0,a-5≤0,
∴a+1-(a-5)=8,
∴此方程无解,故-1≤a≤5不符合题意;
当a>5时,a+1>0,a-5>0,
∴原方程化为a+1+a-5=8,
∴a=6,符合题意,
综上所述,a的值为-2或6.
谢 谢 观 看
第4课时 积的算术平方根
第21章 二次根式
一、选择题
1.将化简,正确的结果是( A )
A.10 B.±10
C.5 D.±5
2.化简二次根式的结果是( A )
A.3 B.-3 C.5 D.15
3.计算×的结果是( D )
A.3 B. C.9 D.3
A
A
D
4.计算并化简3×2,得到的结果是( B )
A.6 B.12 C.6 D.12
5.下列变形正确的是( C )
A.=9
B.=-3
C.()2=-(-1.5)
D.=×
B
C
二、填空题
6.计算:
(1)= 10 ;
(2)= 40 .
7.(1)若=·,则x的取值范围是 1≤x≤4 ;
(2)若=·,则x+3= 5 .
10
40
1≤x≤4
5
三、解答题
8.化简:
(1);
解:原式==×=30.
(2);
解:原式=×=×=.
(3).
解:原式=
=××
=108.
9.计算:
(1)×;
解:原式===5.
(2)5×(-);
解:原式=-5=-15.
(3)××;
解:原式=2×3×3=54.
(4)×.
解:原式=×=10.
一、选择题
10.(1)使等式=-x成立的条件是( C )
A.x<0 B.x≤0
C.-3≤x≤0 D.x为任意实数
(2)若a<b(a,b为非零实数),化简的结果为( A )
A.-a B.a
C.a D.
C
A
(3)设=a,=b,用含a,b的式子表示,则下列表示正确的是( A )
A.0.3ab B.3ab
C.0.1ab2 D.0.1a2b
A
二、解答题
11.计算:
(1)×3×;
解:原式=3×6×=.
(2)·(-);
解:原式=-2×3x=-12x2.
(3)6·;
解:原式=6×=a2.
(4)6·3(y>0);
解:原式=18=108|x3|y.
(5)×(-)×;
解:原式=-
=-4.
(6)(-x)(-)(-2ab).
解:原式=a(-2ab)
=-2a2b|x|.
解答题
12.求+的值.
解:设x=+,
两边平方得:x2=()2+()2+2,即x2=10,
∴x=±,
∵+>0,
∴+=.
请仿照上述方法,求+的值.
解:设x=+,
两边平方得:x2=()2+()2+2,即x2=14,
∴x=±,
∵+>0,
∴+=.
谢 谢 观 看
第5课时 二次根式的除法
第21章 二次根式
一、选择题
1.使等式=成立的条件是( C )
A.x>-2 B.x<9
C.-2≤x<9 D.-2≤x≤9
C
2.(1)计算÷的结果是( B )
A.9 B.3 C.3 D.2
(2)计算-1的结果是( A )
A.1 B. C. D.
(3)计算÷÷的结果是( D )
A. B. C. D.
B
A
D
3.在下列各式中,计算结果不正确的是( A )
A.×=2 B.÷=
C.×= D.÷=
A
二、填空题
4.若=成立,则x的取值范围是 2≤x<4 .
5.计算:
(1)÷= 3 ;
(2)÷(-)= -3 ;
(3)5÷3= ;
(4)= 2 .
2≤x<4
3
-3
2
三、解答题
6.计算:
(1);
解:原式===4.
(2).
解:原式===2.
7.计算:
(1)÷;
解:原式==.
(2)÷;
解:原式===.
(3)6÷(-3);
解:原式=6÷(-3)
=-2
=-4.
(4)2÷.
解:原式=(2÷)=4=12.
8.计算:÷××.
解:原式=
=
=2.
一、选择题
9.在下列运算中,正确的是( B )
A.2·3=6
B.2÷=2
C.===3
D.÷×=÷=1
B
10.若有意义,则的值是( D )
A.非正数 B.负数
C.非负数 D.正数
D
二、解答题
11.计算:
(1)2÷×;
解:原式=2×2÷××
=4××
=.
(2)-4÷.
解:原式=(-4÷)
=-7
=-7.
解答题
12.先来看一个有趣的现象:===2,这里根号里的因数2经过适当的演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”,具有这一性质的数还有许多,如:=3,=4等等.
(1)解:5,
验证:===5;
(2)你能用含正整数n(n≥2)的式子来表示上述规律吗?
(2)解:=n;
(1)猜想:= ,并验证你的猜想;
(4)请你另外再写出1个具有“穿墙”性质的数.
(4)解:=6(答案不唯一).
(3)证明你找到的规律;
(3)证明:===n;
谢 谢 观 看
第6课时 二次根式的化简
第21章 二次根式
一、选择题
1.在下列二次根式中,为最简二次根式的是( B )
A. B.
C. D.
B
2.(1)化简的结果是( A )
A.2 B.4 C.2 D.4
A
(2)把化为最简二次根式得( C )
A.18 B.
C. D.
C
3.若a=,b=1-,则a、b两数的关系是( A )
A.互为相反数 B.互为倒数
C.相等 D.互为负倒数
A
二、填空题
4.(1)把化成最简二次根式为 3 ;
(2)将化为最简二次根式的结果为 .
5.的有理化因式是 .
6.2-3的倒数是 +1 .
3
+1
三、解答题
7.把下列二次根式化简成最简二次根式:
(1);
解:(1)原式==6;
(2);
解:(2)原式==2.
(3);
解:(3)原式===;
(4);
解:(4)原式==.
(5);
解:(5)原式==;
(6).
解:(6)原式==.
8.把下列各式分母有理化:
(1);
解:(1)原式==;
(2);
解:(2)原式===;
(3);
解:(3)原式===.
(4);
解:(4)原式==5+2;
(5).
解:(5)原式==1+.
一、选择题
9.在下列结论中,正确的是( D )
A.是的有理化因式
B.不是最简二次根式
C.3-2的绝对值是3-2
D.3+2的倒数是3-2
10.若xy=3,则x+y的值是( C )
A.2 B.-2 C.±2 D.±
D
C
二、填空题
11.(1)已知+=0,则+的值为 ;
(2)已知a=,b=,则代数式的值为 2 .
2
三、解答题
12.计算:
(1)(m<0);
解:原式=
=-3m.
(2)(x>2).
解:原式=
=
==.
解答题
13.观察下列各式及验证过程:
=,验证:===;
=,验证:===;
=,验证:===.
(1)按照上述三个等式及其验证过程的基本思路,猜想:= ;
解:(1);
(2)按照上述三个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
解:(2)猜想:=,
验证:==
=;
解:(3)=,
理由:
=
=
=.
(3)针对上述各式反映的规律,写出用n(n≥2,且n为自然数)表示的等式,并说明理由.
谢 谢 观 看
第7课时 专题二次根式的乘除
第21章 二次根式
一、选择题
1.(1)下列式子属于最简二次根式的是( A )
A. B. C. D.
(2)在下列二次根式中,为最简二次根式的是( C )
A. B. C. D.
A
C
2.矩形的面积为18,一边长为2,则另一边长为( C )
A.5 B.10 C.3 D.24
3.下列各式计算正确的是( C )
A.=2 B.÷=
C.()2=3 D.=-2
4.已知a=,b=-2,则a与b的关系是( B )
A.a=b B.a=-b
C.a= D.ab=-1
C
C
B
二、填空题
5.计算:×÷= 6 .
6.4-的倒数是 4+ .
6
4+
三、解答题
7.计算:
(1)×;
解:(1)原式===;
(2)÷.
解:(2)原式===3.
8.计算:
(1)×÷×;
解:原式=÷×
=.
(2)9×÷3;
解:原式=(9××)
=
=45.
(3)÷9×(-);
解:原式=×2÷9×(-)
=÷9×(-)
=-.
(4)×4÷().
解:原式=×4×
=3
=18.
9.已知a=,求的值.
解:∵a==2-,
∴a<1,
∴原式=
=
=-
=-2-.
一、选择题
10.已知=a,=b,则=( D )
A. B. C. D.
D
二、填空题
11.当x=2+时,x2-4x+2024= 2023 .
2023
三、解答题
12.计算:
(1)(-)÷3(b<0);
解:原式=·(-b)·(a)÷
=-3a2b÷
=ab.
(2)6a2·5÷15.
解:由题意可得ab>0,
原式=6a2·|a|·5···
=2a2|a|,
当a>0时,原式=2a3,
当a<0时,原式=-2a3.
13.先将÷化简,然后自选一个合适的x值,代入求值.
解:由题意可得x>2,
原式=÷
=·
=,
当x=4时,原式=2.(答案不唯一)
14.计算:÷(÷).(其中b<a<0)
解:原式=·÷(··)
=·÷
=-.
解答题
15.已知+++…+=,求n的值.
解:∵
=
=
=-,
∴+++…+=-+-+…+-=1-,
∴1-=,
∴n=2499.
谢 谢 观 看
第8课时 二次根式的加减
第21章 二次根式
一、选择题
1.与是同类二次根式的是( D )
A. B. C. D.
2.若最简二次根式与最简二次根式是同类二次根式,则x的值为( C )
A.0 B.1 C.2 D.-2
D
C
3.(1)计算-的结果是( C )
A.25 B.2 C. D.5
(2)计算9-的结果是( D )
A. B.- C. D.-
4.下列计算正确的是( A )
A.+=3 B.+=
C.4-3=1 D.3+2=5
C
D
A
二、填空题
5.(1)计算-的结果是 - ;
(2)计算-4的结果是 3 ;
(3)计算2-的结果是 5 .
6.如果与是同类二次根式,那么x的最小正整数值是 4 .
-
3
5
4
三、解答题
7.计算:
(1)+-;
解:原式=2+4-
=5.
(2)9+5-3;
解:原式=9+10-12
=7.
(3)+-3;
解:原式=2+5-
=.
(4)+-;
解:原式=+6-2
=+4.
(5)2+-4;
解:原式=2+2-4×
=2.
(6)+|1-|;
解:原式=3+-1
=4-1.
(7)+-(-4);
解:原式=2+4-+2
=7.
(8)-+-.
解:原式=4-3+18-
=18.
一、选择题
8.下列运算:①+=;②+=2;③3+=3;④=17;⑤=3a+5b.其中正确的有( A )
A.2个 B.3个
C.4个 D.以上都不对
A
二、填空题
9.(1)计算:×-4×= ;
(2)规定:a※b=·+,a*b=ab-b2,试求:3※5= ,2*(-1)= 4-5 .
4-5
三、解答题
10.计算:
(1)+|-2|-(-3)0+()-2;
解:原式=2+2--1+4
=5+.
(2)2-6+-(-);
解:原式=2×2-6×+2-(3-3)
=4-2+2-3+3
=+3.
(3)×(+3-);
解:原式=2×(5+-4)
=12.
(4)-÷2-1+-(+1)0;
解:原式=3-÷+-1-1
=3-1+-1-1
=4-3.
(5)(π-1)0+()-1+|5-|-.
解:原式=1++-5-
=1++3-5-8
=-12.
解答题
11.已知a、b、c为有理数,且使等式a+b+c=成立,求代数式2a+1000b+1023c的值.
解:∵==+,
∴a+b+c=+,
∴a=0,b=1,c=1,
∴2a+1000b+1023c=2023.
谢 谢 观 看
第9课时 二次根式的混合运算
第21章 二次根式
一、选择题
1.在下列各式的计算中,正确的是( D )
A.2+=2 B.4-3=1
C.=x+y D.-=
2.在下列算式中,正确的是( C )
A.3-=3
B.+=
C.(-)2=5-2
D.÷=3
D
C
3.下列计算结果正确的是( A )
A.=-1
B.÷=
C.+=
D.(+)(-)=1
4.下列计算正确的是( D )
A.=-3 B.2-=2
C.5×5=5 D.=--2
A
D
二、填空题
5.(1)计算(-)×+2的结果是 + ;
(2)计算--×的结果是 0 .
6.化简:+= 2-4 .
+
0
2-4
三、解答题
7.计算:
(1)(π-1)0+()-1+|5-|-2;
解:原式=1+2+3-5-2
=-2.
(2)(-)-2-|-2|+÷;
解:原式=4-2++3
=2+4.
(3)÷2+-()0;
解:原式=××+-1-1
=×+-2
=-2.
(4)÷-2×+(+)2.
解:原式=-2+2+2+3
=4-2+5+2
=9.
8.已知x=,y=,求下列各式的值:
(1)x2-xy+y2;
(1)x2-xy+y2=(x+y)2-3xy=;
(2)+.
解:∵x==,y==,
∴x+y=,xy=,
(2)+=
=
=8.
一、填空题
9.计算:
(1)·= +1 ;
(2)(-)2·(5+2)= 1 ;
(3)()2+×+()2= 4 .
+1
1
4
二、解答题
10.计算:
(1)(-2+1)(1+2-);
解:原式=[1-(2-)][1+(2-)]
=1-(2-)2
=1-(8-4+3)
=4-10.
(2)(4+)0-2+(2+)2-.
解:原式=1-4+4+4+3-(+)2
=8-(3+2+2)
=3-2.
11.先化简,再求值:
(1)已知y>++2,求+5-3x的值;
解:根据题意得3x-2≥0,2-3x≥0,
∴x=,
∵y>++2,∴y>2,
∴+5-3x
=+5-3×
=-1+5-2
=2.
(2)已知a=,求-的值.
解:∵a===2-<1,
∴-
=-
=a+3-
=a+3+
=7.
解答题
12.已知x=2+1,求x3-2x2-7x+2023的值.
解:由题意得x-1=2,
∴(x-1)2=8,
∴x2=7+2x,
∴x3-2x2-7x+2023
=x3-x(2x+7)+2023
=x3-x·x2+2023
=2023.
谢 谢 观 看
第10课时 专题二次根式的化简
第21章 二次根式
一、选择题
1.计算(1+)(1-)的结果为( B )
A.2 B.-2 C.3 D.-3
2.若y=+-3,则(x+y)2023的值为( D )
A.1 B.5 C.-5 D.-1
B
D
4.若a,b,c是△ABC的三边长,则化简-的结果是( B )
A.2c B.-2c C.2c-2a D.2a-2b
B
3.计算·的结果为( A )
A.+1 B.-1 C.1- D.1
A
二、填空题
5.已知2<x<3,则化简:|2-x|++= 7-x .
7-x
三、解答题
6.计算:
(1)-(-)(+);
解:原式=2+4+6-(5-3)
=2+4+6-2
=4+6.
(2)++.
解:原式=2++2-
=+2.
7.已知x=+,y=-.
(1)求x+y,xy的值;
解:(1)∵x=+,y=-,
∴x+y=;
xy=()2-()2=1;
解:(2)由(1)知,x+y=,xy=1,
①x2y+xy2=xy(x+y)=;
②+===-2=9.
(2)利用(1)的结果求下列代数式的值:
①x2y+xy2;
②+.
8.观察:因为<<,即2<<3,所以的整数部分为2,小数部分为-2.
请你观察上述规律后解决下列问题:
(1)规定用符号[m]表示实数m的整数部分,例如:[]=0,[]=2.按此规定,则[+1]= ;
解:(1)4;
(2)若的整数部分为a,小数部分为b,|c|=,求c(a-b-6)+12的值.
解:(2)∵<<,即3<<4,
∴a=3,b=-3,
∵|c|=,∴c=±,
当c=时,
c(a-b-6)+12=×(3-+3-6)+12=-11+12=1,
当c=-时,
c(a-b-6)+12=-×(3-+3-6)+12=11+12=23,
综上所述,c(a-b-6)+12的值为1或23.
一、填空题
9.(1)若a为自然数,b为整数,且满足=7-4,则a= 2 ,b= -1 ;
(2)已知a+b=-8,ab=12,那么b+a的值为 - .
2
-1
-
二、解答题
10.若a=,求a4-10a3+a2-20a+5的值.
解:∵a==+5,
∴a-5=,
∴(a-5)2=26,
∴a2-10a+25=26,
∴a2-10a=1,
∴原式=a2(a2-10a)+(a2-10a)-10a+5=a2-10a+6
=7.
解答题
11.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方.例如:4+2=1+3+2=12+2+=.这样小明就找到了一种把类似4+2的式子化为完全平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)结合小明的探索过程填空: =;
解:(1)13+4;
(2)7+4的算术平方根为 ;
解:(2)2+;
(3)化简:+++…+.(n为正整数)
解:(3)原式=+++…+
=-1+-+2-+…+-
=-1.
谢 谢 观 看
第11课时 专题二次根式与勾股定理
第21章 二次根式
一、选择题
1.下列长度的三条线段不能组成直角三角形的是( C )
A.3cm,4cm,5cm B.4cm,3cm,cm
C.6cm,8cm,9cm D.1cm,cm,cm
C
2.如图,由边长为1的小正方形组成的网格中,△ABC的三个顶点A,B,C都在网格的格点上,则下列结论错误的是( D )
第2题图
A.AB= B.AC=5
C.BC=2 D.∠ACB=30°
D
3.古希腊几何学家海伦在他的著作《度量》中,给出了计算三角形面积的海伦公式,若一个三角形三边长分别为a、b、c,记p=,则其面积为S=,如图,利用海伦公式计算△ABC的面积为( C )
第3题图
A. B.5 C. D.3
C
二、填空题
4.已知Rt△ABC的一直角边长为1,斜边长为,则它的另一直角边长为 2 .
5.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是 14 .
第5题图
2
14
三、解答题
6.靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的,则梯子比较稳定.(结果保留根号)
(1)在梯子稳定摆放的情况下,3米的梯子能达到多高的墙头?
解:(1)设梯子放平稳时,可以达到x米高的墙头,
由题意得:x2=32-12,
解得:x=-2(舍去)或2,
答:3米的梯子能达到2米高的墙头;
(2)要达到4米高的墙头,梯子至少要多长?
解:(2)设梯子放平稳时,要达到4米高的墙头,梯子至少要y米,
由题意得:y2=()2+16,
解得:y=-3(舍去)或3,
答:梯子至少要3米长.
7.如图,已知在四边形ABCD中,AB⊥BC,AB=10,BC=5,CD=7,AD=24,求四边形ABCD的面积.
第7题图
解:如图,连接AC,
∵AB⊥BC,AB=10,BC=5,
∴AC==25,
∵CD=7,AD=24,
∴AD2+CD2=625=AC2,
∴△ADC是直角三角形,且∠ADC=90°,
∴S四边形ABCD=S△ABC+S△ADC
=AB·BC+AD·DC
=×10×5+×24×7
=209,
∴四边形ABCD的面积为209.
8.如图,一个正方体木箱子右边连接一个正方形木板,蚂蚁甲从点A出发,沿a,b,d三个面走最短路径到点B;同时蚂蚁乙以相同的速度从点B出发,沿d,c两个面走最短路径到点A.请你通过计算判断哪只蚂蚁先到达目的地?
第8题图
解:如图,展开正方体使a,b,c与d在同一平面内,
∴蚂蚁甲走的路径长为A1B==cm,
蚂蚁乙走的路径长为A2B==cm,
∵cm>cm,
∴蚂蚁乙先到达目的地.
一、填空题
9.如图,正方形ABCD的边长是8,点E在边AB上,AE=,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在点B'处.若△CDB'恰为等腰三角形,则DB'的长为 8或2 .
第9题图
8或2
二、解答题
10.如图,四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,BC=2,AC=,求CD的长.
第10题图
解:如图,把△ABC绕点A逆时针旋转90°,得到△ADE,连接CE,过点E作EF⊥CD延长线于点F,
根据旋转可知:AE=AC=,ED=BC=2,∠ABC=∠ADE,
∵∠ABC+∠BCD+∠ADC+∠DAB=360°,∠BAD=90°,∠BCD=30°,
∴∠ABC+∠ADC=240°,
∴∠ADE+∠ADC=240°,
∴∠EDF=240°-180°=60°,
在Rt△EDF中,∠EDF=60°,
∴DF=DE=1,EF=,
在Rt△AEC中,CE=2,
∴CF==5,
∴CD=CF-DF=4.
解答题
11.如图,已知等腰Rt△ABC,动点P在斜边AB所在的直线上,以PC为直角边作等腰Rt△PCQ,∠PCQ=90°.探究并解决下列问题:
第11题图
(1)如图1,若点P在线段AB上,AC=1+,PA=,则线段PB= ,PC= ;
解:(1),2;
(2)如图2,若点P在AB的延长线上,猜想PA、PB、PC之间的数量关系,并证明;
解:(2)PA2+PB2=2PC2,
证明:如图1,过点C作CD⊥AB,垂足为D,
∵△ACB为等腰直角三角形,
∴CD=AD=DB,
∵AB=PA-PB,∴CD=BD=,
∴PD=BD+PB=,
在Rt△PCD中,PC2=DC2+PD2,
即PC2=()2+()2,
∴PA2+PB2=2PC2;
(3)若动点P满足=,求的值.
解:(3)如图2,过点C作CD⊥AB,垂足为D,
∵=,∴设PA=x,PB=3x,
①当点P1在线段AB上时,AB=P1A+P1B=4x,
∴CD=AD=AB=2x,
∴P1D=AD-P1A=x,
∴P1C==x,
AC==2x,
∴==;
②当点P2在BA的延长线上时,
同理可得P2C=x,AC=x,
∴==,
综上所述,的值为或.
谢 谢 观 看
第12课时 复习巩固
第21章 二次根式
一、选择题
1.使二次根式有意义的条件是( B )
A.x>0 B.x≥0且x≠4
C.x≥0 D.x>0且x≠4
2.在下列根式中,最简二次根式是( A )
A. B. C. D.
B
A
3.化简-()2得( C )
A.2 B.-4x+4
C.x D.5x-2
4.若与已化成最简二次根式,且被开方数相同,则a,b的值分别为( D )
A.-1,1 B.1,-1
C.-1,-1 D.1,1
C
D
5.若实数a,b在数轴上对应点的位置如图所示,化简-|a-b|得( D )
A.2b B.-2b C.2a D.-2a
第5题图
D
二、填空题
6.矩形的面积为12,一边长为2,则另一边长为 3 .
7.在平面直角坐标系中,点P(,-)在第 四 象限.
8.比较大小(填“ >”“=”或“<”):
(1)-4 < -3;
(2)- < -.
3
四
<
<
三、解答题
9.计算:
(1)++;
解:原式=2++2-
=+2.
(2)+4-+;
解:原式=3+2-4+
=5-.
(3)(3-2+)÷2;
解:原式=(6-+4)÷2
=÷2
=.
(4)(1-2)(1+2)-(2-1)2.
解:原式=1-12-(12-4+1)
=-11-13+4
=4-24.
一、选择题
10.(1)已知直角三角形的两直角边的长分别为a=+2,b=-2,则它的斜边长c=( D )
A.12 B.18 C.2 D.3
D
(2)如图,在矩形ABCD中无重叠放入面积分别为8cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( C )
第10(2)题图
A.4cm2
B.(8-12)cm2
C.(4-8)cm2
D.(4+12)cm2
C
二、填空题
11.(1)已知a=-1,则a2+2a+2的值是 12 ;
(2)已知+2=b+8,则的值是 5 ;
(3)已知|2023-a|+=a,求a-20232的值是 2024 ;
(4)已知-=-,=,则a-b= 2 ;
(5)设的整数部分为a,小数部分为b,则的值为 7-12 .
12
5
2024
2
7-12
三、解答题
12.如图,在数轴上有A、B两点表示的数为1、,点B关于点A的对称点为C,设点C表示的数为x,化简求值:--1.
第12题图
解:∵A、B两点表示的数为1、,
∴AB=-1,
∵点B关于点A的对称点为C,
∴AC=AB=-1,
∴OC=1-AC=1-(-1)=2-,
∴x=2-,
∴原式=--1
=-(x+1)-1
=-x-2
=-(2-)-2
=-3+.
解答题
13.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一式子的平方,如4+2=(1+)2,然后小明进行了以下探索:设a+b=(m+n)2(其中a,b,m,n均为整数),则有a+b=m2+3n2+2mn,所以a=m2+3n2,b=2mn,这样小明找到了一种类似a+b的式子化为平方式的方法.
请仿照小明的方法解决下列问题:
(1)当a,b,m,n均为整数时,若a+b=(m+n)2,则a= ,b= ;(用含m,n的代数式表示)
解:(1)∵a+b=(m+n)2=m2+5n2+2mn,
∴a=m2+5n2,b=2mn,
故答案为:m2+5n2,2mn;
(2)请找一组正整数填空: + =( + )2;
解:(2)令m=2,n=1,
由(1)可得a=m2+5n2=9,b=2mn=4,
∴9+4=(2+)2,
故答案为:9,4,2,1(答案不唯一);
(3)若a+4=(m+n)2,且a,m,n均为正整数,求a的值.
解:(3)由(1)可得a=m2+5n2,b=2mn=4,
∴mn=2,
∵m,n均为正整数,
∴m=2,n=1或m=1,n=2,
∴a=m2+5n2=22+5×12=9或a=m2+5n2=12+5×22=21,
综上所述,a的值为9或21.
谢 谢 观 看
第1课时 二次根式(1)
第21章 二次根式
一、选择题
1.下列各式中,一定是二次根式的有( B )
①;②;③;④;⑤.
A.2个 B.3个 C.4个 D.5个
2.在下列各式中,一定是二次根式的是( D )
A. B.
C. D.
B
D
4.二次根式中,x的取值范围是( D )
A.x≥1 B.x≤1 C.x>1 D.x<1
D
3.若二次根式有意义,则( C )
A.x≠2 B.x>2 C.x≤2 D.x≥2
C
二、填空题
5.(1)使二次根式有意义的x的取值范围是 x≤2 ;
(2)当x ≥-1且x≠2 时,在实数范围内有意义.
x≤2
≥-1且x≠2
三、解答题
6.计算:
(1)()2;
解:(1)()2=4;
(2)()2;
解:(2)()2=.
(3)()2;
解:(3)()2=0;
(4)(-)2;
解:(4)(-)2=0.6.
(5)(3)2;
解:(5)(3)2=18;
(6)(-3)2.
解:(6)(-3)2=2.
7.当x取何值时,下列各式在实数范围内有意义?
(1)+;
解:要使有意义,则3-x≥0,即x≤3,
要使有意义,则x-2≥0,即x≥2,
∴当2≤x≤3时,+有意义.
(2);
解:∵1-=1-|x|,
∴当x=±1时,1-|x|=0,原式没有意义,
∴当x≠±1时,有意义.
(3)+;
解:要使有意义,则2x≥0,即x≥0,
要使有意义,则-2x≥0,即x≤0,
∴当x=0时,+有意义.
(4).
解:要使有意义,则x+2≥0且3x≠0,
即x≥-2且x≠0,
∴当x≥-2且x≠0时,有意义.
8.已知y=++4,求的值.
解:根据题意得,解得x=3,
将x=3代入y=++4,得y=4,
∴x2+y2=25,∴=5.
一、填空题
9.使代数式+有意义的整数x的和是 -6 .
-6
二、解答题
10.(1)若a、b为实数,且b=,求-的值;
解:由题意得,a2-1≥0,1-a2≥0,
∴a2=1,即a=±1,
∵a+1≠0,∴a≠-1,
∴a=1,
∴b==,
∴-=-=-3.
(2)已知|x-1000|+()2=2000,y=++,求y-x的平方根;
解:由题意得,998-x≥0,m-1≥0,1-m≥0,m+8≥0,
解得x≤998,m=1,
∴1000-x+998-x=2000,
解得x=-1,
∴y=++=3,
∴y-x=3-(-1)=4,
∴y-x的平方根是±2.
(3)与|3-a-|是相反数,求+的值.
解:由题意得+|3-a-|=0,
∴3-a-=0,解得a+=3,
∴a+2+=5,
∴(+)2=5,
∴+=.
解答题
11.观察下列各式:
=1+=1+;
=1+=1+;
=1+=1+;
…,
请利用你发现的规律,计算:
+++…+.
解:原式=1++1++1++…+1+
=2023+-+…+
=2023+1-
=2023.
谢 谢 观 看
第2课时 二次根式(2)
第21章 二次根式
一、选择题
1.下列式子是二次根式的是( C )
A. B.
C. D.
2.二次根式的值为( D )
A.-2 B.±2 C.4 D.2
C
D
4.在下列各式中,正确的是( C )
A.=±4 B.=-4
C.-=-4 D.=a
C
3.已知=a-1,那么a的取值范围为( B )
A.a>1 B.a≥1 C.a<1 D.a≤1
B
二、填空题
5.(1)化简:= -2 ;
(2)已知a<0,b>0,化简:= b-a .
6.若=3-b,则b应满足 b≤3 .
-2
b-a
b≤3
三、解答题
7.化简:
(1);
解:(1)=0.3;
(2);
解:(2)==0.6.
(3);
解:(3)=|-|=;
(4)-;
解:(4)-=-|-π|=-π.
(5)+|3-x|(x<2).
解:(5)原式=+|3-x|
=2-x+3-x
=5-2x.
8.(1)计算:+;
解:原式=+
=π-3+5-π
=2.
(2)化简:+(2≤x≤3).
解:∵2≤x≤3,
∴x-2≥0,x-3≤0,
∴原式=+
=+
=x-2+3-x
=1.
9.实数a,b在数轴上的位置如图所示,化简:+|a+b|+.
第9题图
解:由数轴可知,-2<a<-1,2<b<3,
∴a+1<0,a+b>0,b-3<0,
原式=+(a+b)+|b-3|
=-(a+1)+(a+b)+(3-b)
=2.
一、选择题
10.(1)计算()2+的结果是( C )
A.-1 B.2x-5 C.5-2x D.1
(2)若式子+的值为2,则a的取值范围是( D )
A.a≤4 B.a≥2
C.a=2或4 D.2≤a≤4
C
D
二、解答题
11.(1)a、b、c都是实数,且|a|+a=0,=1,|c|-c=0.试求-|a+b|-+|c-a|的值;
解:由题意得a<0,b<0,c≥0,
∴-|a+b|-+|c-a|
=-b+(a+b)-(c-b)+(c-a)
=b.
(2)若实数x,y,m满足关系式+=·,求m的值.
解:依题意,得,解得x+y=20,
∴+=0,
∴3x+3y-m=0,
∴m=3(x+y)=60,
即m的值是60.
解答题
12.阅读下列材料,回答问题:
在化简的过程中,小张和小李的化简结果不同.
小张的化简如下:
=
==-;
小李的化简如下:
=
==-.
(1)请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由;
解:(1)小李的化简结果正确,小张的化简结果错误.理由如下:
∵<,∴-<0,
∴=|-|=-(-)=-;
(2)请你利用上面正确的方法化简:
①;②.
解:(2)①原式===+1;
②原式===-1.
谢 谢 观 看
第3课时 二次根式的乘法
第21章 二次根式
一、选择题
1.如果·=成立,那么a满足的条件是( C )
A.a≥-2 B.-2≤a≤3
C.a≥3 D.a为一切实数
2.在下列各数中,与的积仍为无理数的是( D )
A. B. C. D.
C
D
3.下列运算:①2×3=6;②4·=4;③2·3=3;④×=,其中正确的有( B )
A.0个 B.1个 C.2个 D.3个
B
二、填空题
4.如果等式·=成立,那么有x+1 ≥ 0,1-x ≥ 0,所以x的取值范围是 -1≤x≤1 .
5.计算:
≥
≥
-1≤x≤1
(1)2×= 2 ;
(2)×= 3 ;
(3)×= 3 ;
(4)2×= 2 ;
(5)×3= 6 .
2
3
3
2
6
6.矩形的长和宽分别为和,则这个矩形的面积为 .
7.如果·=0,那么a= 6 .
6
三、解答题
8.计算:
(1)×;
解:原式==.
(2)×;
解:原式==10.
(3)×;
解:原式==9.
(4)×;
解:原式==1.2.
(5)×;
解:原式==.
(6)4×(-3);
解:原式=-12×=-48.
(7)××;
解:原式=×=2.
(8)2×3×;
解:原式=(2×3)
=6×
=120.
(9)××.
解:原式===3.
一、选择题
9.计算·的结果为( D )
A. B. C.13 D.1
D
二、解答题
10.已知一个长方体的长、宽、高分别为3cm、2cm、2cm.求这个长方体的体积.
解:∵长方体的长、宽、高分别为3cm、2cm、2cm,
∴3×2×2=3×2×2=72cm3,
答:这个长方体的体积为72cm3.
解答题
11.阅读下列解题过程:
例:若代数式+的值是2,求a的取值范围.
解:原式=|a-1|+|a-3|,
当a<1时,原式=(1-a)+(3-a)=4-2a=2,解得a=1(舍去);
当1≤a≤3时,原式=(a-1)+(3-a)=2=2,符合条件;
当a>3时,原式=(a-1)+(a-3)=2a-4=2,解得a=3(舍去),
综上所述,a的取值范围是1≤a≤3.
上述解题过程主要运用了分类讨论的方法,请你根据上述方法,解答下列问题:
(1)当2≤a≤5时,化简:+;
解:(1)∵2≤a≤5,
∴a-2≥0,a-5≤0,
∴原式=|a-2|+|a-5|
=a-2-(a-5)
=3;
(2)若等式+=4成立,求a的取值范围;
解:(2)由题意可知:|3-a|+|a-7|=4,
当a<3时,3-a>0,a-7<0,
∴原方程化为3-a-(a-7)=4,
∴a=3(舍去);
当3≤a≤7时,3-a≤0,a-7≤0,
∴原方程化为-(3-a)-(a-7)=4,
∴4=4,故3≤a≤7符合题意;
当a>7时,3-a<0,a-7>0,
∴原方程化为-(3-a)+(a-7)=4,
∴a=7(舍去),
综上所述,a的取值范围是3≤a≤7;
(3)若+=8,求a的值.
解:(3)原方程可化为|a+1|+|a-5|=8,
当a<-1时,a+1<0,a-5<0,
∴原方程化为-(a+1)-(a-5)=8,
∴a=-2,符合题意;
当-1≤a≤5时,a+1≥0,a-5≤0,
∴a+1-(a-5)=8,
∴此方程无解,故-1≤a≤5不符合题意;
当a>5时,a+1>0,a-5>0,
∴原方程化为a+1+a-5=8,
∴a=6,符合题意,
综上所述,a的值为-2或6.
谢 谢 观 看
第4课时 积的算术平方根
第21章 二次根式
一、选择题
1.将化简,正确的结果是( A )
A.10 B.±10
C.5 D.±5
2.化简二次根式的结果是( A )
A.3 B.-3 C.5 D.15
3.计算×的结果是( D )
A.3 B. C.9 D.3
A
A
D
4.计算并化简3×2,得到的结果是( B )
A.6 B.12 C.6 D.12
5.下列变形正确的是( C )
A.=9
B.=-3
C.()2=-(-1.5)
D.=×
B
C
二、填空题
6.计算:
(1)= 10 ;
(2)= 40 .
7.(1)若=·,则x的取值范围是 1≤x≤4 ;
(2)若=·,则x+3= 5 .
10
40
1≤x≤4
5
三、解答题
8.化简:
(1);
解:原式==×=30.
(2);
解:原式=×=×=.
(3).
解:原式=
=××
=108.
9.计算:
(1)×;
解:原式===5.
(2)5×(-);
解:原式=-5=-15.
(3)××;
解:原式=2×3×3=54.
(4)×.
解:原式=×=10.
一、选择题
10.(1)使等式=-x成立的条件是( C )
A.x<0 B.x≤0
C.-3≤x≤0 D.x为任意实数
(2)若a<b(a,b为非零实数),化简的结果为( A )
A.-a B.a
C.a D.
C
A
(3)设=a,=b,用含a,b的式子表示,则下列表示正确的是( A )
A.0.3ab B.3ab
C.0.1ab2 D.0.1a2b
A
二、解答题
11.计算:
(1)×3×;
解:原式=3×6×=.
(2)·(-);
解:原式=-2×3x=-12x2.
(3)6·;
解:原式=6×=a2.
(4)6·3(y>0);
解:原式=18=108|x3|y.
(5)×(-)×;
解:原式=-
=-4.
(6)(-x)(-)(-2ab).
解:原式=a(-2ab)
=-2a2b|x|.
解答题
12.求+的值.
解:设x=+,
两边平方得:x2=()2+()2+2,即x2=10,
∴x=±,
∵+>0,
∴+=.
请仿照上述方法,求+的值.
解:设x=+,
两边平方得:x2=()2+()2+2,即x2=14,
∴x=±,
∵+>0,
∴+=.
谢 谢 观 看
第5课时 二次根式的除法
第21章 二次根式
一、选择题
1.使等式=成立的条件是( C )
A.x>-2 B.x<9
C.-2≤x<9 D.-2≤x≤9
C
2.(1)计算÷的结果是( B )
A.9 B.3 C.3 D.2
(2)计算-1的结果是( A )
A.1 B. C. D.
(3)计算÷÷的结果是( D )
A. B. C. D.
B
A
D
3.在下列各式中,计算结果不正确的是( A )
A.×=2 B.÷=
C.×= D.÷=
A
二、填空题
4.若=成立,则x的取值范围是 2≤x<4 .
5.计算:
(1)÷= 3 ;
(2)÷(-)= -3 ;
(3)5÷3= ;
(4)= 2 .
2≤x<4
3
-3
2
三、解答题
6.计算:
(1);
解:原式===4.
(2).
解:原式===2.
7.计算:
(1)÷;
解:原式==.
(2)÷;
解:原式===.
(3)6÷(-3);
解:原式=6÷(-3)
=-2
=-4.
(4)2÷.
解:原式=(2÷)=4=12.
8.计算:÷××.
解:原式=
=
=2.
一、选择题
9.在下列运算中,正确的是( B )
A.2·3=6
B.2÷=2
C.===3
D.÷×=÷=1
B
10.若有意义,则的值是( D )
A.非正数 B.负数
C.非负数 D.正数
D
二、解答题
11.计算:
(1)2÷×;
解:原式=2×2÷××
=4××
=.
(2)-4÷.
解:原式=(-4÷)
=-7
=-7.
解答题
12.先来看一个有趣的现象:===2,这里根号里的因数2经过适当的演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”,具有这一性质的数还有许多,如:=3,=4等等.
(1)解:5,
验证:===5;
(2)你能用含正整数n(n≥2)的式子来表示上述规律吗?
(2)解:=n;
(1)猜想:= ,并验证你的猜想;
(4)请你另外再写出1个具有“穿墙”性质的数.
(4)解:=6(答案不唯一).
(3)证明你找到的规律;
(3)证明:===n;
谢 谢 观 看
第6课时 二次根式的化简
第21章 二次根式
一、选择题
1.在下列二次根式中,为最简二次根式的是( B )
A. B.
C. D.
B
2.(1)化简的结果是( A )
A.2 B.4 C.2 D.4
A
(2)把化为最简二次根式得( C )
A.18 B.
C. D.
C
3.若a=,b=1-,则a、b两数的关系是( A )
A.互为相反数 B.互为倒数
C.相等 D.互为负倒数
A
二、填空题
4.(1)把化成最简二次根式为 3 ;
(2)将化为最简二次根式的结果为 .
5.的有理化因式是 .
6.2-3的倒数是 +1 .
3
+1
三、解答题
7.把下列二次根式化简成最简二次根式:
(1);
解:(1)原式==6;
(2);
解:(2)原式==2.
(3);
解:(3)原式===;
(4);
解:(4)原式==.
(5);
解:(5)原式==;
(6).
解:(6)原式==.
8.把下列各式分母有理化:
(1);
解:(1)原式==;
(2);
解:(2)原式===;
(3);
解:(3)原式===.
(4);
解:(4)原式==5+2;
(5).
解:(5)原式==1+.
一、选择题
9.在下列结论中,正确的是( D )
A.是的有理化因式
B.不是最简二次根式
C.3-2的绝对值是3-2
D.3+2的倒数是3-2
10.若xy=3,则x+y的值是( C )
A.2 B.-2 C.±2 D.±
D
C
二、填空题
11.(1)已知+=0,则+的值为 ;
(2)已知a=,b=,则代数式的值为 2 .
2
三、解答题
12.计算:
(1)(m<0);
解:原式=
=-3m.
(2)(x>2).
解:原式=
=
==.
解答题
13.观察下列各式及验证过程:
=,验证:===;
=,验证:===;
=,验证:===.
(1)按照上述三个等式及其验证过程的基本思路,猜想:= ;
解:(1);
(2)按照上述三个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
解:(2)猜想:=,
验证:==
=;
解:(3)=,
理由:
=
=
=.
(3)针对上述各式反映的规律,写出用n(n≥2,且n为自然数)表示的等式,并说明理由.
谢 谢 观 看
第7课时 专题二次根式的乘除
第21章 二次根式
一、选择题
1.(1)下列式子属于最简二次根式的是( A )
A. B. C. D.
(2)在下列二次根式中,为最简二次根式的是( C )
A. B. C. D.
A
C
2.矩形的面积为18,一边长为2,则另一边长为( C )
A.5 B.10 C.3 D.24
3.下列各式计算正确的是( C )
A.=2 B.÷=
C.()2=3 D.=-2
4.已知a=,b=-2,则a与b的关系是( B )
A.a=b B.a=-b
C.a= D.ab=-1
C
C
B
二、填空题
5.计算:×÷= 6 .
6.4-的倒数是 4+ .
6
4+
三、解答题
7.计算:
(1)×;
解:(1)原式===;
(2)÷.
解:(2)原式===3.
8.计算:
(1)×÷×;
解:原式=÷×
=.
(2)9×÷3;
解:原式=(9××)
=
=45.
(3)÷9×(-);
解:原式=×2÷9×(-)
=÷9×(-)
=-.
(4)×4÷().
解:原式=×4×
=3
=18.
9.已知a=,求的值.
解:∵a==2-,
∴a<1,
∴原式=
=
=-
=-2-.
一、选择题
10.已知=a,=b,则=( D )
A. B. C. D.
D
二、填空题
11.当x=2+时,x2-4x+2024= 2023 .
2023
三、解答题
12.计算:
(1)(-)÷3(b<0);
解:原式=·(-b)·(a)÷
=-3a2b÷
=ab.
(2)6a2·5÷15.
解:由题意可得ab>0,
原式=6a2·|a|·5···
=2a2|a|,
当a>0时,原式=2a3,
当a<0时,原式=-2a3.
13.先将÷化简,然后自选一个合适的x值,代入求值.
解:由题意可得x>2,
原式=÷
=·
=,
当x=4时,原式=2.(答案不唯一)
14.计算:÷(÷).(其中b<a<0)
解:原式=·÷(··)
=·÷
=-.
解答题
15.已知+++…+=,求n的值.
解:∵
=
=
=-,
∴+++…+=-+-+…+-=1-,
∴1-=,
∴n=2499.
谢 谢 观 看
第8课时 二次根式的加减
第21章 二次根式
一、选择题
1.与是同类二次根式的是( D )
A. B. C. D.
2.若最简二次根式与最简二次根式是同类二次根式,则x的值为( C )
A.0 B.1 C.2 D.-2
D
C
3.(1)计算-的结果是( C )
A.25 B.2 C. D.5
(2)计算9-的结果是( D )
A. B.- C. D.-
4.下列计算正确的是( A )
A.+=3 B.+=
C.4-3=1 D.3+2=5
C
D
A
二、填空题
5.(1)计算-的结果是 - ;
(2)计算-4的结果是 3 ;
(3)计算2-的结果是 5 .
6.如果与是同类二次根式,那么x的最小正整数值是 4 .
-
3
5
4
三、解答题
7.计算:
(1)+-;
解:原式=2+4-
=5.
(2)9+5-3;
解:原式=9+10-12
=7.
(3)+-3;
解:原式=2+5-
=.
(4)+-;
解:原式=+6-2
=+4.
(5)2+-4;
解:原式=2+2-4×
=2.
(6)+|1-|;
解:原式=3+-1
=4-1.
(7)+-(-4);
解:原式=2+4-+2
=7.
(8)-+-.
解:原式=4-3+18-
=18.
一、选择题
8.下列运算:①+=;②+=2;③3+=3;④=17;⑤=3a+5b.其中正确的有( A )
A.2个 B.3个
C.4个 D.以上都不对
A
二、填空题
9.(1)计算:×-4×= ;
(2)规定:a※b=·+,a*b=ab-b2,试求:3※5= ,2*(-1)= 4-5 .
4-5
三、解答题
10.计算:
(1)+|-2|-(-3)0+()-2;
解:原式=2+2--1+4
=5+.
(2)2-6+-(-);
解:原式=2×2-6×+2-(3-3)
=4-2+2-3+3
=+3.
(3)×(+3-);
解:原式=2×(5+-4)
=12.
(4)-÷2-1+-(+1)0;
解:原式=3-÷+-1-1
=3-1+-1-1
=4-3.
(5)(π-1)0+()-1+|5-|-.
解:原式=1++-5-
=1++3-5-8
=-12.
解答题
11.已知a、b、c为有理数,且使等式a+b+c=成立,求代数式2a+1000b+1023c的值.
解:∵==+,
∴a+b+c=+,
∴a=0,b=1,c=1,
∴2a+1000b+1023c=2023.
谢 谢 观 看
第9课时 二次根式的混合运算
第21章 二次根式
一、选择题
1.在下列各式的计算中,正确的是( D )
A.2+=2 B.4-3=1
C.=x+y D.-=
2.在下列算式中,正确的是( C )
A.3-=3
B.+=
C.(-)2=5-2
D.÷=3
D
C
3.下列计算结果正确的是( A )
A.=-1
B.÷=
C.+=
D.(+)(-)=1
4.下列计算正确的是( D )
A.=-3 B.2-=2
C.5×5=5 D.=--2
A
D
二、填空题
5.(1)计算(-)×+2的结果是 + ;
(2)计算--×的结果是 0 .
6.化简:+= 2-4 .
+
0
2-4
三、解答题
7.计算:
(1)(π-1)0+()-1+|5-|-2;
解:原式=1+2+3-5-2
=-2.
(2)(-)-2-|-2|+÷;
解:原式=4-2++3
=2+4.
(3)÷2+-()0;
解:原式=××+-1-1
=×+-2
=-2.
(4)÷-2×+(+)2.
解:原式=-2+2+2+3
=4-2+5+2
=9.
8.已知x=,y=,求下列各式的值:
(1)x2-xy+y2;
(1)x2-xy+y2=(x+y)2-3xy=;
(2)+.
解:∵x==,y==,
∴x+y=,xy=,
(2)+=
=
=8.
一、填空题
9.计算:
(1)·= +1 ;
(2)(-)2·(5+2)= 1 ;
(3)()2+×+()2= 4 .
+1
1
4
二、解答题
10.计算:
(1)(-2+1)(1+2-);
解:原式=[1-(2-)][1+(2-)]
=1-(2-)2
=1-(8-4+3)
=4-10.
(2)(4+)0-2+(2+)2-.
解:原式=1-4+4+4+3-(+)2
=8-(3+2+2)
=3-2.
11.先化简,再求值:
(1)已知y>++2,求+5-3x的值;
解:根据题意得3x-2≥0,2-3x≥0,
∴x=,
∵y>++2,∴y>2,
∴+5-3x
=+5-3×
=-1+5-2
=2.
(2)已知a=,求-的值.
解:∵a===2-<1,
∴-
=-
=a+3-
=a+3+
=7.
解答题
12.已知x=2+1,求x3-2x2-7x+2023的值.
解:由题意得x-1=2,
∴(x-1)2=8,
∴x2=7+2x,
∴x3-2x2-7x+2023
=x3-x(2x+7)+2023
=x3-x·x2+2023
=2023.
谢 谢 观 看
第10课时 专题二次根式的化简
第21章 二次根式
一、选择题
1.计算(1+)(1-)的结果为( B )
A.2 B.-2 C.3 D.-3
2.若y=+-3,则(x+y)2023的值为( D )
A.1 B.5 C.-5 D.-1
B
D
4.若a,b,c是△ABC的三边长,则化简-的结果是( B )
A.2c B.-2c C.2c-2a D.2a-2b
B
3.计算·的结果为( A )
A.+1 B.-1 C.1- D.1
A
二、填空题
5.已知2<x<3,则化简:|2-x|++= 7-x .
7-x
三、解答题
6.计算:
(1)-(-)(+);
解:原式=2+4+6-(5-3)
=2+4+6-2
=4+6.
(2)++.
解:原式=2++2-
=+2.
7.已知x=+,y=-.
(1)求x+y,xy的值;
解:(1)∵x=+,y=-,
∴x+y=;
xy=()2-()2=1;
解:(2)由(1)知,x+y=,xy=1,
①x2y+xy2=xy(x+y)=;
②+===-2=9.
(2)利用(1)的结果求下列代数式的值:
①x2y+xy2;
②+.
8.观察:因为<<,即2<<3,所以的整数部分为2,小数部分为-2.
请你观察上述规律后解决下列问题:
(1)规定用符号[m]表示实数m的整数部分,例如:[]=0,[]=2.按此规定,则[+1]= ;
解:(1)4;
(2)若的整数部分为a,小数部分为b,|c|=,求c(a-b-6)+12的值.
解:(2)∵<<,即3<<4,
∴a=3,b=-3,
∵|c|=,∴c=±,
当c=时,
c(a-b-6)+12=×(3-+3-6)+12=-11+12=1,
当c=-时,
c(a-b-6)+12=-×(3-+3-6)+12=11+12=23,
综上所述,c(a-b-6)+12的值为1或23.
一、填空题
9.(1)若a为自然数,b为整数,且满足=7-4,则a= 2 ,b= -1 ;
(2)已知a+b=-8,ab=12,那么b+a的值为 - .
2
-1
-
二、解答题
10.若a=,求a4-10a3+a2-20a+5的值.
解:∵a==+5,
∴a-5=,
∴(a-5)2=26,
∴a2-10a+25=26,
∴a2-10a=1,
∴原式=a2(a2-10a)+(a2-10a)-10a+5=a2-10a+6
=7.
解答题
11.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方.例如:4+2=1+3+2=12+2+=.这样小明就找到了一种把类似4+2的式子化为完全平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)结合小明的探索过程填空: =;
解:(1)13+4;
(2)7+4的算术平方根为 ;
解:(2)2+;
(3)化简:+++…+.(n为正整数)
解:(3)原式=+++…+
=-1+-+2-+…+-
=-1.
谢 谢 观 看
第11课时 专题二次根式与勾股定理
第21章 二次根式
一、选择题
1.下列长度的三条线段不能组成直角三角形的是( C )
A.3cm,4cm,5cm B.4cm,3cm,cm
C.6cm,8cm,9cm D.1cm,cm,cm
C
2.如图,由边长为1的小正方形组成的网格中,△ABC的三个顶点A,B,C都在网格的格点上,则下列结论错误的是( D )
第2题图
A.AB= B.AC=5
C.BC=2 D.∠ACB=30°
D
3.古希腊几何学家海伦在他的著作《度量》中,给出了计算三角形面积的海伦公式,若一个三角形三边长分别为a、b、c,记p=,则其面积为S=,如图,利用海伦公式计算△ABC的面积为( C )
第3题图
A. B.5 C. D.3
C
二、填空题
4.已知Rt△ABC的一直角边长为1,斜边长为,则它的另一直角边长为 2 .
5.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是 14 .
第5题图
2
14
三、解答题
6.靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的,则梯子比较稳定.(结果保留根号)
(1)在梯子稳定摆放的情况下,3米的梯子能达到多高的墙头?
解:(1)设梯子放平稳时,可以达到x米高的墙头,
由题意得:x2=32-12,
解得:x=-2(舍去)或2,
答:3米的梯子能达到2米高的墙头;
(2)要达到4米高的墙头,梯子至少要多长?
解:(2)设梯子放平稳时,要达到4米高的墙头,梯子至少要y米,
由题意得:y2=()2+16,
解得:y=-3(舍去)或3,
答:梯子至少要3米长.
7.如图,已知在四边形ABCD中,AB⊥BC,AB=10,BC=5,CD=7,AD=24,求四边形ABCD的面积.
第7题图
解:如图,连接AC,
∵AB⊥BC,AB=10,BC=5,
∴AC==25,
∵CD=7,AD=24,
∴AD2+CD2=625=AC2,
∴△ADC是直角三角形,且∠ADC=90°,
∴S四边形ABCD=S△ABC+S△ADC
=AB·BC+AD·DC
=×10×5+×24×7
=209,
∴四边形ABCD的面积为209.
8.如图,一个正方体木箱子右边连接一个正方形木板,蚂蚁甲从点A出发,沿a,b,d三个面走最短路径到点B;同时蚂蚁乙以相同的速度从点B出发,沿d,c两个面走最短路径到点A.请你通过计算判断哪只蚂蚁先到达目的地?
第8题图
解:如图,展开正方体使a,b,c与d在同一平面内,
∴蚂蚁甲走的路径长为A1B==cm,
蚂蚁乙走的路径长为A2B==cm,
∵cm>cm,
∴蚂蚁乙先到达目的地.
一、填空题
9.如图,正方形ABCD的边长是8,点E在边AB上,AE=,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在点B'处.若△CDB'恰为等腰三角形,则DB'的长为 8或2 .
第9题图
8或2
二、解答题
10.如图,四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,BC=2,AC=,求CD的长.
第10题图
解:如图,把△ABC绕点A逆时针旋转90°,得到△ADE,连接CE,过点E作EF⊥CD延长线于点F,
根据旋转可知:AE=AC=,ED=BC=2,∠ABC=∠ADE,
∵∠ABC+∠BCD+∠ADC+∠DAB=360°,∠BAD=90°,∠BCD=30°,
∴∠ABC+∠ADC=240°,
∴∠ADE+∠ADC=240°,
∴∠EDF=240°-180°=60°,
在Rt△EDF中,∠EDF=60°,
∴DF=DE=1,EF=,
在Rt△AEC中,CE=2,
∴CF==5,
∴CD=CF-DF=4.
解答题
11.如图,已知等腰Rt△ABC,动点P在斜边AB所在的直线上,以PC为直角边作等腰Rt△PCQ,∠PCQ=90°.探究并解决下列问题:
第11题图
(1)如图1,若点P在线段AB上,AC=1+,PA=,则线段PB= ,PC= ;
解:(1),2;
(2)如图2,若点P在AB的延长线上,猜想PA、PB、PC之间的数量关系,并证明;
解:(2)PA2+PB2=2PC2,
证明:如图1,过点C作CD⊥AB,垂足为D,
∵△ACB为等腰直角三角形,
∴CD=AD=DB,
∵AB=PA-PB,∴CD=BD=,
∴PD=BD+PB=,
在Rt△PCD中,PC2=DC2+PD2,
即PC2=()2+()2,
∴PA2+PB2=2PC2;
(3)若动点P满足=,求的值.
解:(3)如图2,过点C作CD⊥AB,垂足为D,
∵=,∴设PA=x,PB=3x,
①当点P1在线段AB上时,AB=P1A+P1B=4x,
∴CD=AD=AB=2x,
∴P1D=AD-P1A=x,
∴P1C==x,
AC==2x,
∴==;
②当点P2在BA的延长线上时,
同理可得P2C=x,AC=x,
∴==,
综上所述,的值为或.
谢 谢 观 看
第12课时 复习巩固
第21章 二次根式
一、选择题
1.使二次根式有意义的条件是( B )
A.x>0 B.x≥0且x≠4
C.x≥0 D.x>0且x≠4
2.在下列根式中,最简二次根式是( A )
A. B. C. D.
B
A
3.化简-()2得( C )
A.2 B.-4x+4
C.x D.5x-2
4.若与已化成最简二次根式,且被开方数相同,则a,b的值分别为( D )
A.-1,1 B.1,-1
C.-1,-1 D.1,1
C
D
5.若实数a,b在数轴上对应点的位置如图所示,化简-|a-b|得( D )
A.2b B.-2b C.2a D.-2a
第5题图
D
二、填空题
6.矩形的面积为12,一边长为2,则另一边长为 3 .
7.在平面直角坐标系中,点P(,-)在第 四 象限.
8.比较大小(填“ >”“=”或“<”):
(1)-4 < -3;
(2)- < -.
3
四
<
<
三、解答题
9.计算:
(1)++;
解:原式=2++2-
=+2.
(2)+4-+;
解:原式=3+2-4+
=5-.
(3)(3-2+)÷2;
解:原式=(6-+4)÷2
=÷2
=.
(4)(1-2)(1+2)-(2-1)2.
解:原式=1-12-(12-4+1)
=-11-13+4
=4-24.
一、选择题
10.(1)已知直角三角形的两直角边的长分别为a=+2,b=-2,则它的斜边长c=( D )
A.12 B.18 C.2 D.3
D
(2)如图,在矩形ABCD中无重叠放入面积分别为8cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( C )
第10(2)题图
A.4cm2
B.(8-12)cm2
C.(4-8)cm2
D.(4+12)cm2
C
二、填空题
11.(1)已知a=-1,则a2+2a+2的值是 12 ;
(2)已知+2=b+8,则的值是 5 ;
(3)已知|2023-a|+=a,求a-20232的值是 2024 ;
(4)已知-=-,=,则a-b= 2 ;
(5)设的整数部分为a,小数部分为b,则的值为 7-12 .
12
5
2024
2
7-12
三、解答题
12.如图,在数轴上有A、B两点表示的数为1、,点B关于点A的对称点为C,设点C表示的数为x,化简求值:--1.
第12题图
解:∵A、B两点表示的数为1、,
∴AB=-1,
∵点B关于点A的对称点为C,
∴AC=AB=-1,
∴OC=1-AC=1-(-1)=2-,
∴x=2-,
∴原式=--1
=-(x+1)-1
=-x-2
=-(2-)-2
=-3+.
解答题
13.阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一式子的平方,如4+2=(1+)2,然后小明进行了以下探索:设a+b=(m+n)2(其中a,b,m,n均为整数),则有a+b=m2+3n2+2mn,所以a=m2+3n2,b=2mn,这样小明找到了一种类似a+b的式子化为平方式的方法.
请仿照小明的方法解决下列问题:
(1)当a,b,m,n均为整数时,若a+b=(m+n)2,则a= ,b= ;(用含m,n的代数式表示)
解:(1)∵a+b=(m+n)2=m2+5n2+2mn,
∴a=m2+5n2,b=2mn,
故答案为:m2+5n2,2mn;
(2)请找一组正整数填空: + =( + )2;
解:(2)令m=2,n=1,
由(1)可得a=m2+5n2=9,b=2mn=4,
∴9+4=(2+)2,
故答案为:9,4,2,1(答案不唯一);
(3)若a+4=(m+n)2,且a,m,n均为正整数,求a的值.
解:(3)由(1)可得a=m2+5n2,b=2mn=4,
∴mn=2,
∵m,n均为正整数,
∴m=2,n=1或m=1,n=2,
∴a=m2+5n2=22+5×12=9或a=m2+5n2=12+5×22=21,
综上所述,a的值为9或21.
谢 谢 观 看
